基于改进粒子群优化的探地雷达波形反演算法

郑 适 张安学 岳思橙 蒋延生



基于改进粒子群优化的探地雷达波形反演算法

郑 适 张安学*岳思橙 蒋延生

(西安交通大学电信学院 西安 710049)

探地雷达工作的最终目的是反演解释地下结构参数，由于大多数反演问题是非线性的，研究非线性的反演方法具有重要意义。该文提出基于改进粒子群优化方法的探地雷达反演问题，该算法以信号均方误差为目标函数，用时域有限差分方法作为正演工具。通过与基于遗传算法等反演方法的结果对比，说明了该算法兼顾了准确性和简便性；通过对模型复杂、参数多、信噪比差的仿真数据的反演结果，说明了该算法对多参数反演的有效性和良好的抗噪性；对实测数据的反演结果，进一步验证了该算法的可行性。

探地雷达；反演算法；非线性；粒子群优化

1 引言

粒子群反演算法在模型空间中随机地进行全局搜索，不容易陷入局部最小，同时，该方法具有实施简便、易于施加先验约束条件、适于并行计算等优点[13,14]。本文提出了基于改进PSO的探地雷达反演算法，应用时域有限差分方法[15]作为正演手段，以信号均方误差作为目标函数，将改进的PSO方法应用于探地雷达的反演问题中。对仿真数据和实测数据的反演结果，说明了该方法的可行性和有效性。本文首先介绍PSO的基本原理，阐述应用改进PSO的探地雷达反演算法，然后分析仿真数据的反演结果，最后在此基础上处理探地雷达实测数据并分析反演结果。

2 算法描述

2.1 基于粒子群优化的探地雷达反演算法

在探地雷达中，接收波形既包含信号的幅度信息，又包含相位与反射波的时延等信息。为了有效利用反射信号的所有信息，以波形的差异作为反演的目标函数，即实际接收信号与模型正演信号的均方误差：

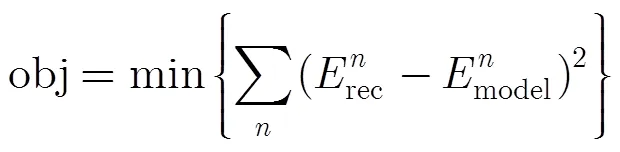
粒子群优化的思想基于生物学中关于群体智能的研究成果。对鸟群飞行的研究发现，一只鸟仅追踪它有限数量的邻居，但最终的整体结果似乎在一个中心的控制之下，即复杂的全局行为是由简单规则的相互作用引起的。PSO即源于对鸟群捕食行为的研究。假设某区域内的一群鸟正在随机搜索食物，此区域内只有一块食物，每只鸟均不知晓食物的具体位置，但却知晓各自距食物的距离，同时它们之间可以互相通信，那么合理的搜索策略即是每只鸟都向距离食物最近的那只鸟移动。PSO算法即从这种模型中得到启示而产生。在PSO算法模型中，优化问题的每一个潜在解对应搜索空间中的一只鸟，称之为“粒子”。每个粒子都有一个适应值和速度，适应值由目标函数决定，速度决定它飞行的方向和距离。各个粒子记忆、追随当前的最优粒子。算法将优化问题的解初始化为一群随机粒子，在每次迭代中，粒子通过跟踪两个极值——个体极值点和全局极值点来更新自己。个体极值点是粒子本身在其有限的邻居中找到的最优解，这些邻居是整个种群的一部分而不是全部；全局极值点是整个种群中所有粒子的最优解。

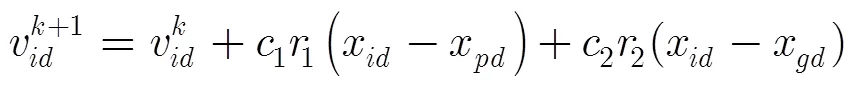
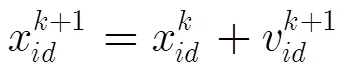
2.2 基于改进粒子群优化的探地雷达反演算法

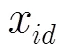
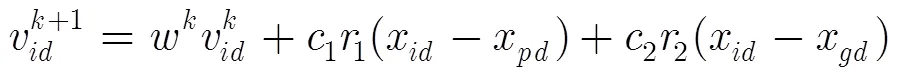
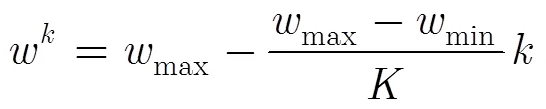
3 仿真数据及野外实测数据反演结果

3.1 仿真数据反演结果

3.1.1与基于原始粒子群的反演方法和基于遗传算法的反演方法的结果对比 构造一个包含2层结构的地层模型，分层的几何构造及每层的相对介电常数如图2(a)所示。上下两层媒质的相对介电常数分别为5, 12。两层媒质的分界面具有一定倾斜程度，斜率=0.05，分界面起点深度=0.8 m，设定横向探测距离为1.5 m，纵向最大探测深度为2.0 m。设天线距离地面的距离为0.5 m，接收天线与发射天线之间距离为0.2 m，由FDTD正演得到的回波信号如图2(b)所示。

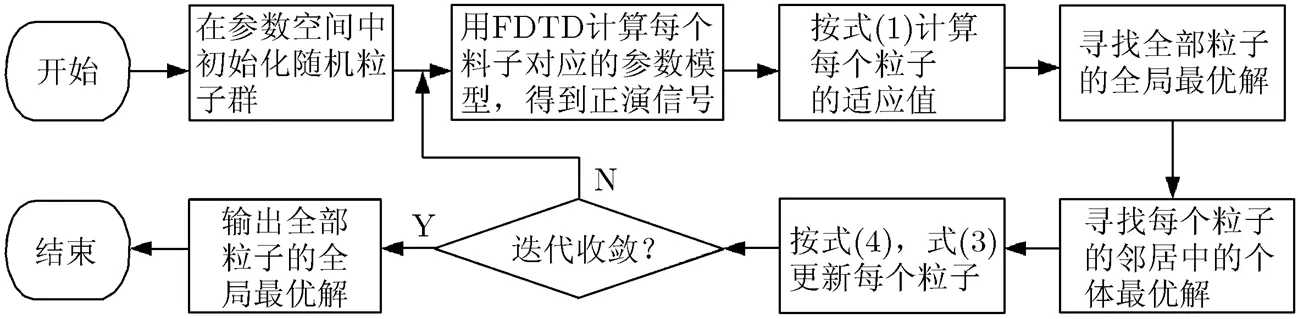
图1 基于改进PSO的探地雷达反演算法流程图

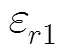
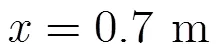
表1反演算法结果

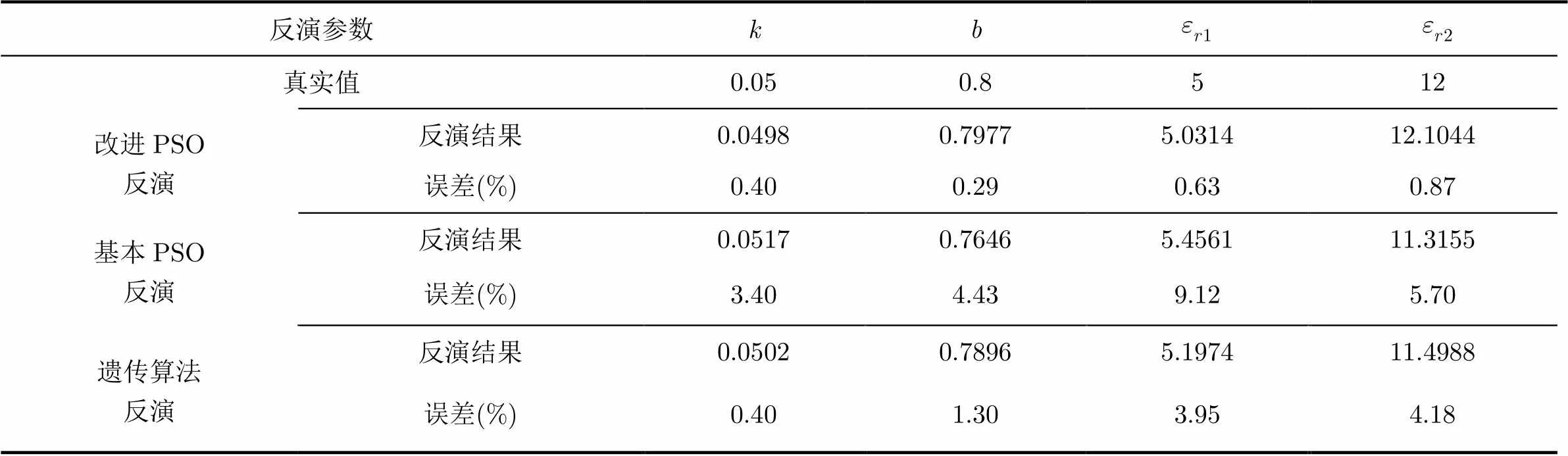
反演参数kb 真实值0.050.8512 改进PSO反演反演结果0.04980.79775.031412.1044 误差(%)0.400.290.630.87 基本PSO反演反演结果0.05170.76465.456111.3155 误差(%)3.404.439.125.70 遗传算法反演反演结果0.05020.78965.197411.4988 误差(%)0.401.303.954.18

图3 3种反演方法的结果对比

3.1.2复杂模型的反演 建立复杂的地下模型如图4(a)所示。

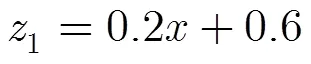
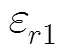
3.2 野外实测数据的反演

3.2.1实例1 为了验证本文算法对实测数据的有效性，本文作者进行了实地测量，针对野外采集到的雷达接收数据，用本文算法进行反演。采集地点为西安交通大学西一楼侧面路面施工处。探地雷达型号为美国地球物理测量系统公司的TerraSIRchSIR -3000型探地雷达，天线频率为900 MHz，时窗长度为25 ns，测量模式为距离(测量轮控制测量)模式。路基分层照片如图6(a)所示，该路基上面两层分别为水泥层和混杂有杂物的黏土层，水泥层厚度约为16 cm，黏土层厚度约为50 cm。黏土层以下还有其他分层，但由于测量时窗为50 ns，黏土层以下媒质的反射信息将不包括在接收信号中，因此反演时不考虑黏土层以下的结构。探地雷达接收数据如图6(b)所示。

图4 复杂的地层模型及其正演回波信号

表2复杂模型的反演结果

反演参数 真实值0.20.6-0.20.31.25128 无噪反演结果误差(%)0.20090.6035-0.20030.30261.20264.949311.85347.8813 0.440.590.150.870.221.011.221.48 加噪反演结果误差(%)0.20220.6037-0.20350.30951.20364.942211.74597.4597 1.110.621.733.170.301.162.126.75

表3实测数据的反演结果

反演参数 反演结果0.16514.500013.9277

3.2.2实例2 本文作者用同一探地雷达系统对中国某铁路隧道衬砌进行了实际测量，测量场景如图8(a)所示，实测数据如图8(b)所示。应用基于改进PSO的方法对这段实测数据进行反演，结果如图8(c)和图8(d)所示。图8(c)绘出了隧道衬砌厚度解释曲线；用反演出的模型作正演，得到的反演数据如图8(d)。将图8(c)厚度解释曲线的结果与钻孔测量厚度的结果比较，两者基本吻合，说明基于改进PSO的反演方法准确估计了衬砌厚度。从图8(d)的反演数据和图8(b)的实测数据比较看来，该反演算法达到了较为理想的效果。从图8(d)的整个反演剖面来看，该反演算法能够适应媒质电磁参数的横向变化，能够清楚刻画衬砌层与底层的分界面。

4 结束语

本文将改进的粒子群优化算法应用于探地雷达反演问题中，用信号的均方误差作为优化目标函数，以时域有限差分方法作为正演工具，提出基于改进PSO的探地雷达反演算法。首先描述该算法的原理和实现过程，然后通过对仿真数据和实测数据的处理，准确反演得到了地下模型结构，验证了该算法的有效性和可行性。在反演结果中，将该算法与基于原始PSO的反演方法和常用的基于遗传算法的反演方法作对比，证明了本算法具有更高的准确率，同时算法实施起来更简便；另外，采用本算法对模型复杂、参数较多、信噪比较差情况下的仿真数据进行反演，结果说明了该算法可以有效地反演多参数模型，同时具有良好的抗噪性；最后，将本算法应用于实测数据，反演结果与实际情况吻合度较高，说明了该算法对实测数据的有效性。多种情况的实验结果共同验证了该算法的可行性。

图6 实测场景及数据

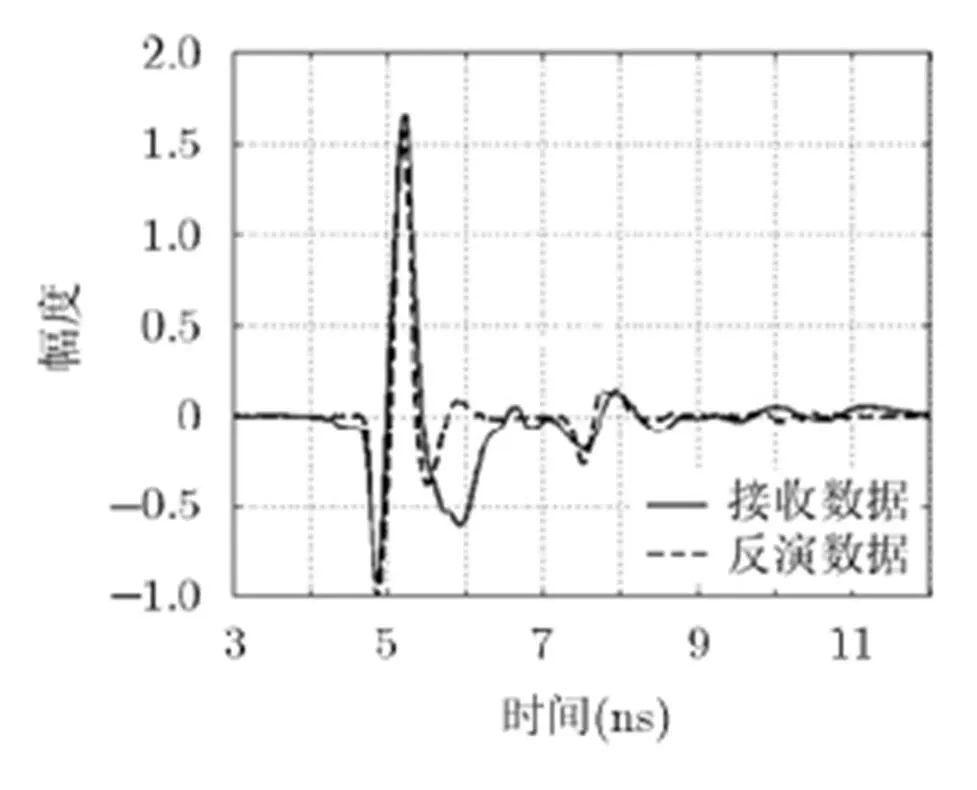
图7 实测数据的反演结果

图8 实例数据的测量与反演结果

[1] Neal A. Ground-penetrating radar and its use in sedimentology: principles, problems and progress[J].-, 2004,66(3/4): 261-330.

[2] 王家映. 地球物理反演理论[M]. 武汉: 中国地质大学出版社, 2002: 1-3.

Wang Jia-ying. Geophysical Inverse Theory[M]. Wuhan: China University of Geoscience Press, 2002: 1-3.

[3] Spagnolini U and Rampa V. Multitarget detection/tracking for monostatic ground penetrating radar: application to pavement profiling[J]., 1999,37(1): 383-394.

[4] 黄忠来, 张建中, 黄吉林. 探地雷达薄层信号的谱反演算法[J]. 大地测量与地球动力学, 2011,31(4): 154-159.

Huang Zhong-lai, Zhang Jian-zhong, and Huang Ji-lin. A sepectral inversion algorithm for GPR signals of thin layers[J]., 2011, 31(4): 154-159.

[5] 俞燕浓, 方广有. 一种反演地下介质参数的新算法[J]. 电子与信息学报, 2009,31(03): 619-622.

Yu Yan-nong and Fang Guang-you. A new algorithm for underground medium parameters inversion[J].&, 2009, 31(03): 619-622.

[6] Khan T and Smirnova A. 1D inverse problem in diffusion based optical tomography using iteratively regularized Gauss-Newton algorithm[J]., 2005,161(1): 149-170.

[7] Gustafsson M and He S L. A wave-splitting based optimization approach to multi-dimensional time-domain electromagnetic inverse problems[J]., 1999,50(5/6): 541-551.

[8] Chang Xu-hua and Wang Yan-ming. Coal fire depth-profile reconstruction from ground penetrating radar data[J]., 2012,15(11A): 4647-4652.

[9] Aghasi A, Mendoza-Sanchez I, and Miller E L. A geometric approach to joint inversion with applications to contaminant source zone characterization[J]., 2013,29(11). DOI: 10.1088/0266-5611/29/11/115014.

[10] 易远元, 王家映. 粒子群反演方法[J]. 工程地球物理学报, 2009,6(4): 385-389.

Yi Yuan-yuan and Wang Jia-ying. Particle swarm optimization inversion method[J]., 2009, 6(4): 385-389.

[11] Yan Z and Gu H. Non-linear prestack seismic inversion with global optimization using an edge-preserving smoothing filter[J]., 2013,61(4): 747-760.

[12] Chiu Chien-ching and Li Jhuo-ru. Image reconstruction of perfectly conducting objects by a cascaded method[J]., 2013,219(11): 6093-6105.

[13] Cui Y, Ji T, Li X,. Inversion of multi-anomalies in resistivity profiling based on particle swarm optimization[J]., 2013,28(4): 2164-2170.

[14] Toushmalani R. Gravity inversion of a fault by particle swarm optimization (PSO)[J]., 2013, 2: 315.

[15] Werner G R, Bauer C A and Cary J R. A more accurate, stable, FDTD algorithm for electromagnetics in anisotropic dielectrics[J]., 2013,255(12): 436-455.

[16] Shi Y H and Eberhart R. A modified particle swarm optimizer[C]. 1998 IEEE International Conference on Evolutionary Computation, Anchorage, 1998: 69-73.

[17] Shi Y and Eberhart R. Empirical study of particle swarm optimization[C]. Proceedings of the 1999 Congress on Evolutionary Computation-CEC99(Cat. No. 99TH8406), Washington DC, 1999: 1945-1950.

[18] 舒志乐. 隧道衬砌内空洞探地雷达探测正反演研究[D]. [博士论文], 重庆大学, 2010.

Shu Zhi-le. Study on GPR forward simulation and inversion of tunnel lining cavity[D]. [Ph.D. dissertation], Chongqing University, 2010.

郑 适： 女，1990年生，博士生，研究方向为探地雷达信号处理.

张安学： 男，1972年生，教授，研究方向为天线阵列信号处理、超宽带雷达系统及其目标成像、检测、识别算法研究，电磁场数值计算，超材料理论及其应用研究等.

Ground Penetrating Radar Inversion Algorithm Based on Improved Particle Swarm Optimization

Zheng Shi Zhang An-xue Yue Si-cheng Jiang Yan-sheng

(,’,’710049,)

Inversion and interpretation of underground structure are ultimate aim of Ground Penetrating Radar (GPR) working. Most of inversion problems are non-linear, hence, investigations of non-linear inversion methods are significant. In this paper, an improved Particle Swarm Optimization (PSO) is used to solve GPR inverse problem. Comparison results with other inversion including the genetic algorithm show that the proposed method has higher accuracy and better simplicity; inversion results under a condition of complicated model, multi- parameter and low SNR indicate the effectiveness dealing with multi-parameter and better anti-noise ability of the proposed algorithm; the inversion results of actual measurement data further verify the feasibility of this algorithm.

Ground Penetrating Radar (GPR); Inversion algorithm; Non-linear; Particle Swarm Optimization (PSO)

TN959.3

A

1009-5896(2014)11-2717-06

10.3724/SP.J.1146.2013.01979

张安学 anxuezhang@mail.xjtu.edu.cn

2013-12-19收到，2014-04-03改回

国家自然科学基金(61331005, 61001039)和中国科学院电磁辐射与探测技术重点实验室资助课题