基于空域稀疏性的嵌套MIMO雷达DOA估计算法

杨 杰 廖桂生



基于空域稀疏性的嵌套MIMO雷达DOA估计算法

杨 杰*廖桂生

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

针对传统MIMO雷达可分辨目标数受限于虚拟阵元数的问题，该文提出一种基于嵌套阵的MIMO雷达阵形设计新方法并改进了相应的稀疏DOA估计算法。首先分析对传统MIMO雷达的虚拟阵元进行嵌套采样给DOA估计性能带来的影响；然后提出嵌套MIMO雷达阵形设计方法，在虚拟阵元数相同的情况下，该阵形比传统阵形分辨更多的目标；最后提出一种基于空域稀疏性的嵌套MIMO雷达改进DOA估计算法，该算法使用噪声子空间加权，在提高分辨率的同时可以有效消除伪峰。仿真结果验证了该文算法的有效性和优越性。

MIMO雷达；嵌套阵；波达方向；空域稀疏；噪声子空间加权

1 引言

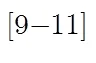
2 信号模型

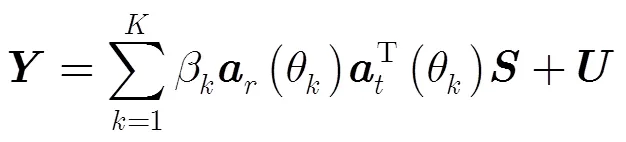
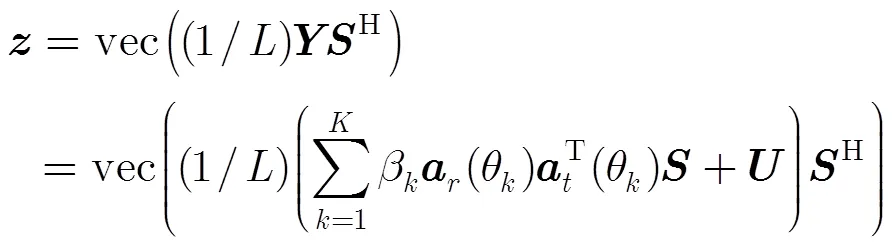
由于MIMO雷达的发射信号相互正交，故式(2)可简化为

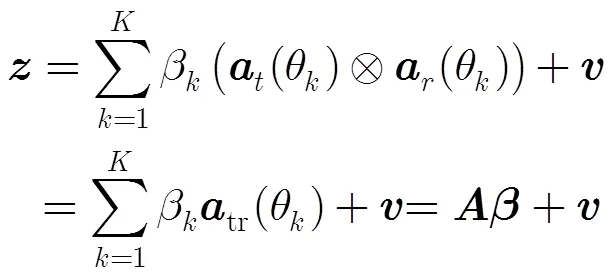
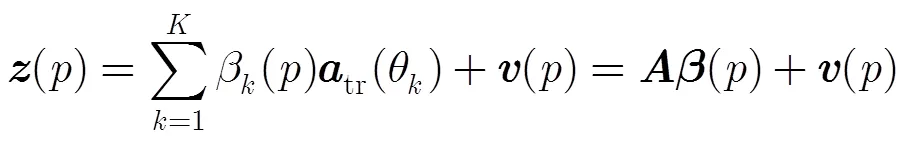
由以上分析可知

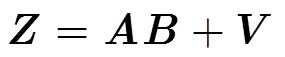
3 基于嵌套阵的MIMO雷达阵形设计

3.1基于KR积的接收信号预处理

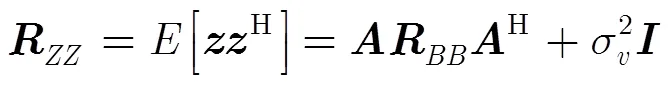
向量化协方差矩阵，得

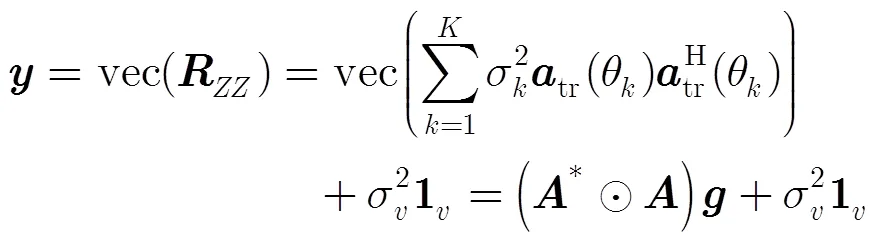
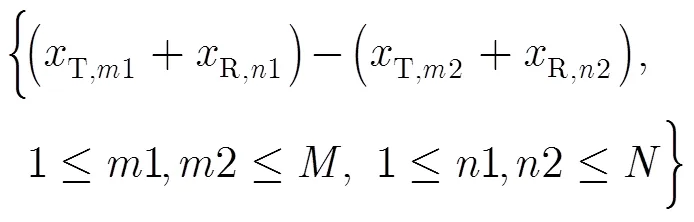
3.2 基于嵌套采样的数据降维处理

由图1可知，嵌套采样从12个虚拟阵元中抽取一半阵元进行DOA估计。由图2可知，嵌套采样后系统自由度保持不变(最多可估计11个目标的DOA)。因此，实际中可利用部分虚拟阵元实现全阵元时的DOA估计效果，从而降低数据处理量。

3.3 基于嵌套阵的MIMO雷达阵形设计

本节讨论基于嵌套阵的MIMO雷达阵形设计方法，以突破传统阵形对自由度的限制。

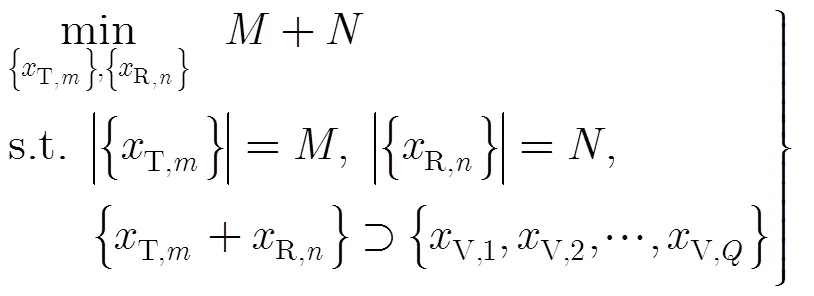
通过计算机搜索求解式(9)，可得到嵌套MIMO雷达的阵形配置。与同收发阵元数目的MIMO雷达相比，嵌套MIMO雷达自由度更大，可以解决前者存在的欠定DOA估计问题。

下面简单验证上述结论。假设我们期望得到虚拟阵元数为8的嵌套MIMO雷达阵形，经计算机搜索可得到多组解，图3所示为其中一组解。

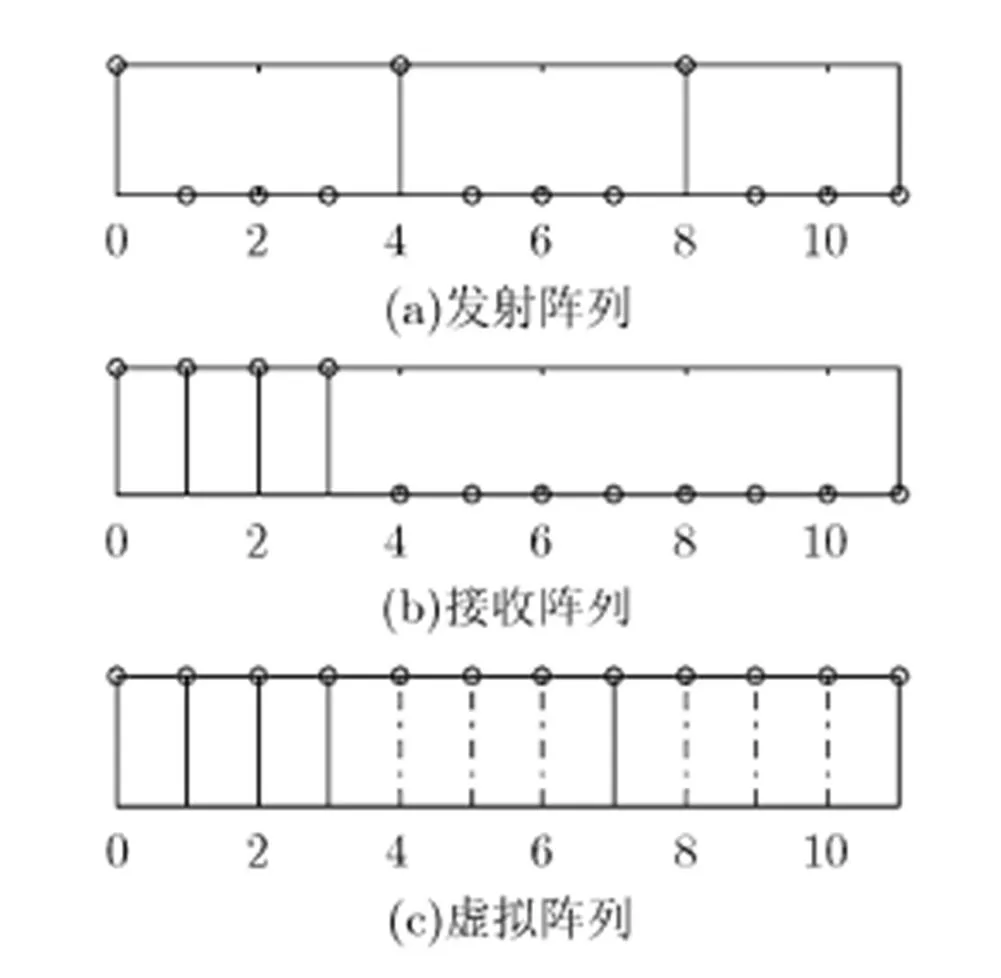
图1 基于嵌套采样的MIMO雷达阵形

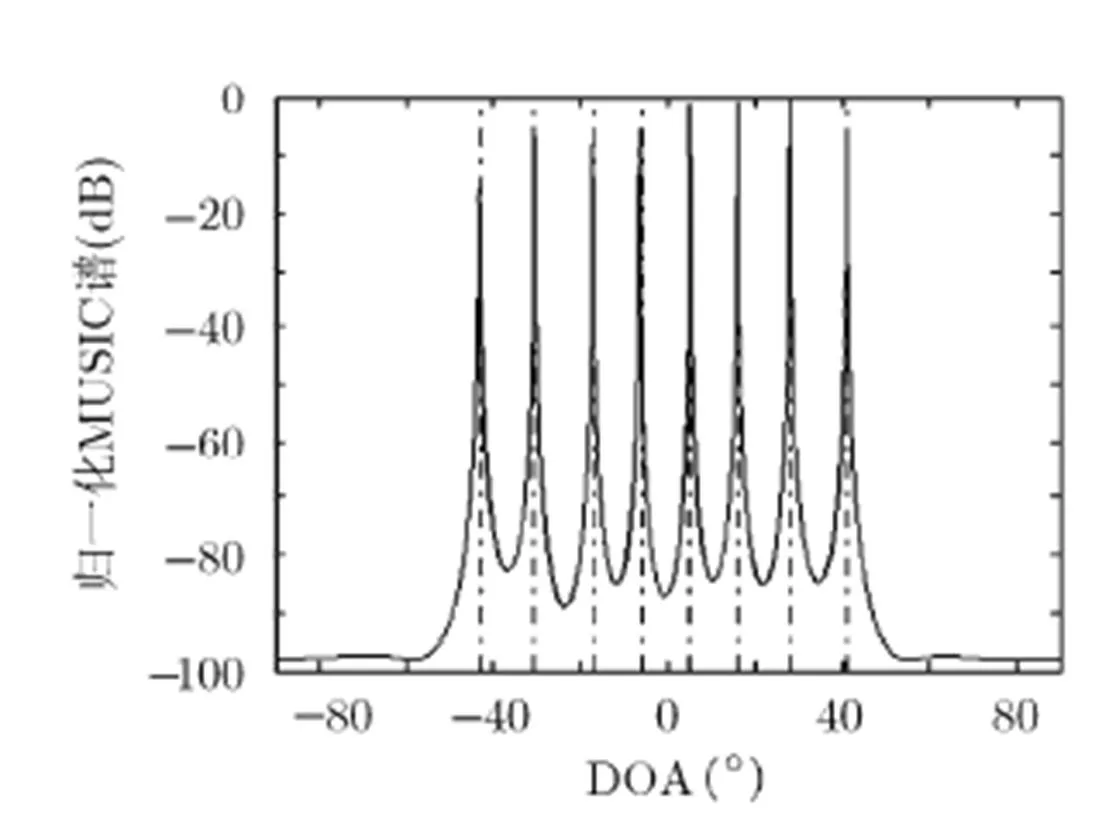
图2 基于嵌套采样的MIMO雷达DOA估计结果(K=8)

图3 嵌套MIMO雷达阵形

由图3可知，嵌套MIMO雷达收发阵元数与图1相同。当信噪比为5 dB，快拍数为300时，比较图1，图3所示两种阵形的DOA估计结果，如图4所示。由于嵌套MIMO雷达扩展了等效虚拟孔径，因此谱峰更尖锐，空间分辨率更高。

假设信噪比为5 dB，快拍数为300。图5所示为采用图3阵形的DOA估计结果。由于采用图1阵形最多可估计11个目标的DOA，因此由图5可知，嵌套MIMO雷达可有效解决非嵌套MIMO雷达中存在的欠定DOA估计问题。

4 基于嵌套MIMO雷达的稀疏DOA估计算法

4.1 SMV稀疏模型

稀疏表示类DOA估计算法利用来波空域稀疏的先验信息，将DOA估计转化为从测量矢量中重构稀疏信号的问题。以式(7)为例，可以将其改写为如式(10)所示的SMV稀疏模型。

4.2 本文算法

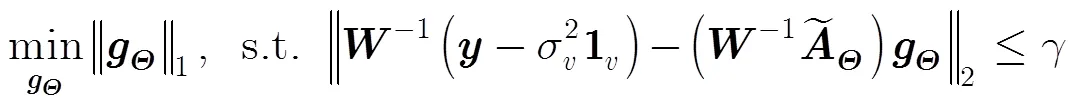
式(11)为二阶锥规划(Second Order Cone Programming, SOCP)问题，可利用CVX工具包求解。本质上，稀疏度应通过L0范数表征，然而求解L0范数约束的优化问题通常是NP难的，因此式(11)采用L1范数松弛，导致求解结果易出现伪峰。为了消除此缺陷，本文提出一种改进的稀疏DOA估计算法，该算法利用噪声子空间与目标扩展阵列流形矩阵的正交性构造基于加权L1范数约束的凸优化问题，从而提高对L0范数近似的精确度。

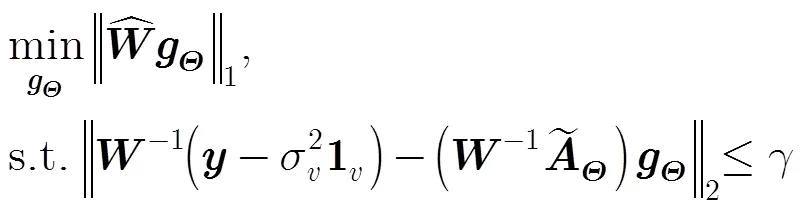
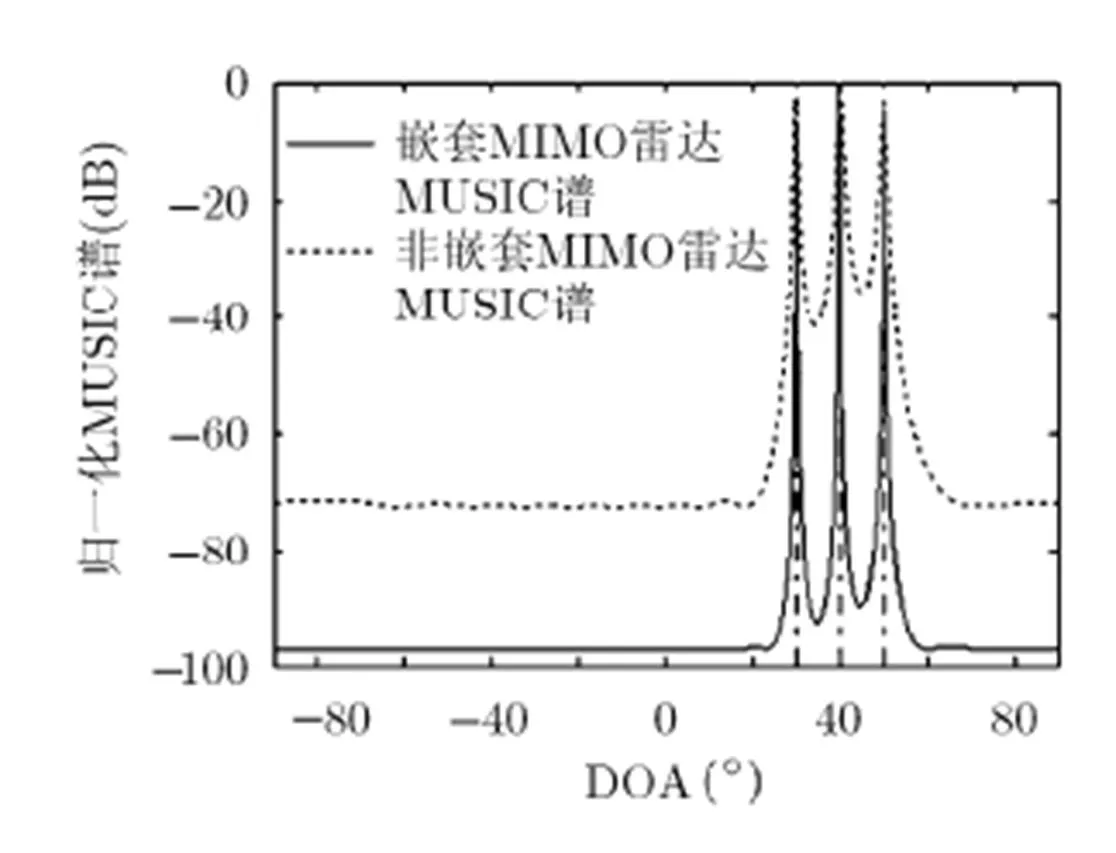
图4 嵌套及非嵌套MIMO雷达DOA估计结果对比(K=3)

式(13)可化为如式(14)所示的标准SOC形式：

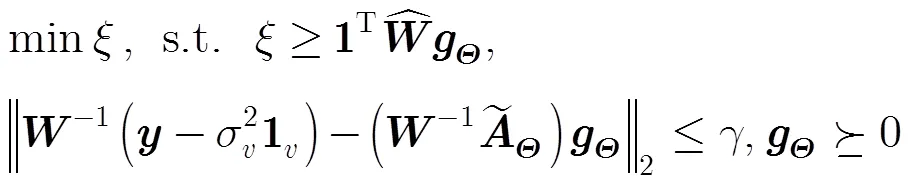
图6所示为MUSIC方法，L1-L2方法和本文方法DOA估计效果的对比。嵌套MIMO雷达阵形如图3所示，信噪比为5 dB，快拍数为300。

由图6可知，MUSIC方法分辨率最低，本文方法分辨率最高且可有效消除L1-L2方法估计结果中存在的伪峰。

5 算法复杂度分析

6 仿真与分析

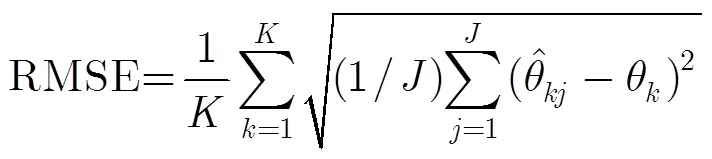
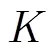
仿真1=3时各算法DOA估计性能

由图7和图8可知，由于存在空间间隔较近的目标，因此传统子空间类算法(MUSIC算法)的DOA估计性能最差。与其他稀疏DOA估计类算法(SPICE算法，JLZA算法)相比，本文算法具有较好的DOA估计性能。这是由于JLZA算法直接基于接收数据进行处理，所利用的阵列自由度有限；SPICE算法虽然利用式(10)所示的信号模型合成虚拟差分阵元提升自由度，但此时相当于文献[9]中所述的单测量矢量情形，与理想的多测量矢量情形相比，估计精度有所下降；本文算法是基于式(10)所示的单测量矢量模型推导出来的且利用加权L1范数促进解的稀疏化，既充分利用了嵌套阵的自由度扩展特性，又提高了空间角度分辨率，因此本文算法的估计性能最接近CRLB。

仿真2=13时各算法DOA估计性能

由图9和图10可知，本文算法具有最优的估计性能，同时由于目标个数增多，因此与仿真1的结果相比，各算法的DOA估计性能均有不同程度的下降。

仿真3 各算法角度分辨性能

由图11和图12可知，在不同SNR、不同快拍数情形下，本文算法的角度分辨性能最好，MUSIC算法的角度分辨性能最差，这是由于SPICE算法和本文算法均为半参数方法，分辨性能通常优于非参数方法(如MUSIC算法)。

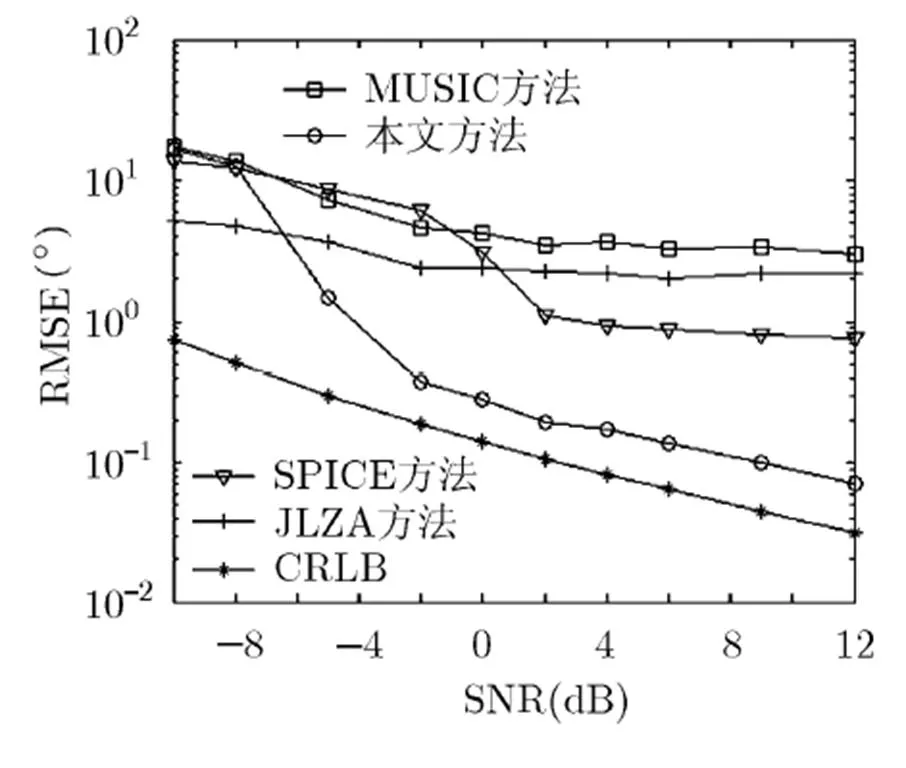
图7 RMSE随SNR的变化曲线(K=3)

图8 RMSE随快拍数的变化曲线(K=3)

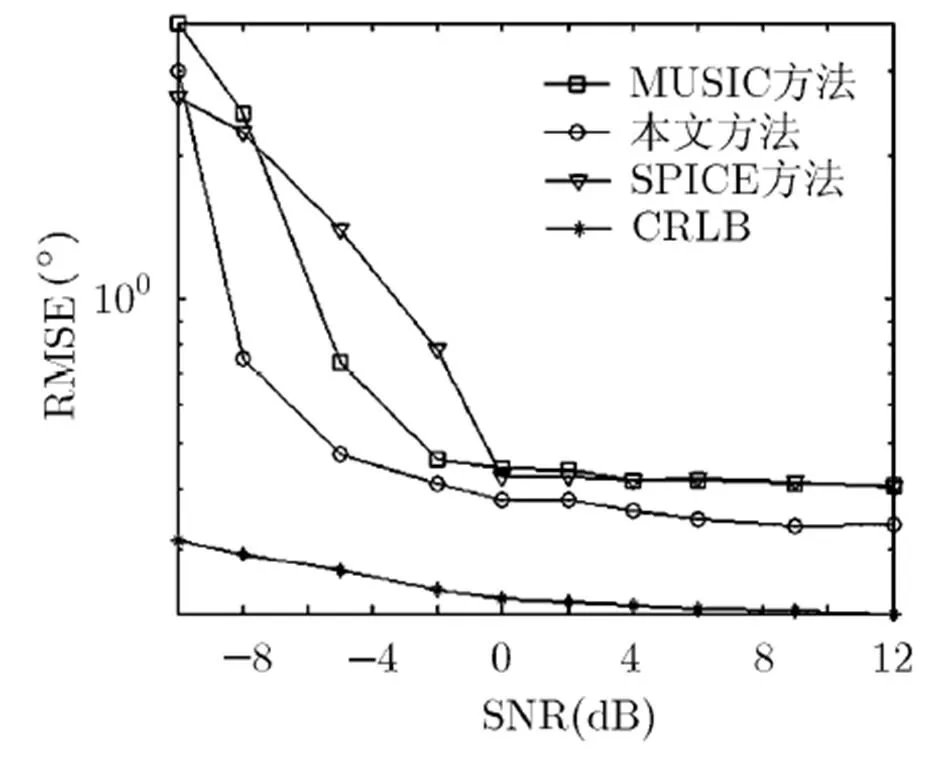
图9 RMSE随SNR的变化曲线(K=13)

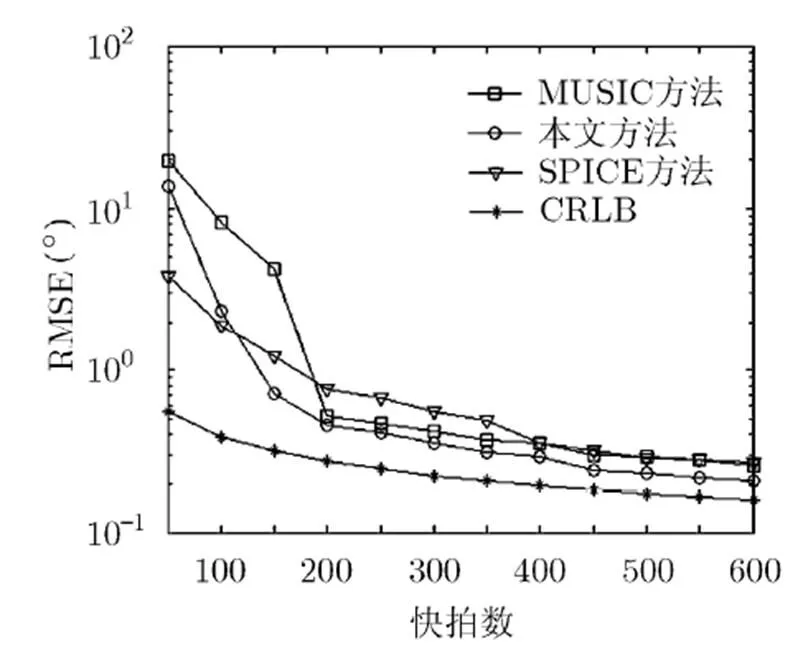
图10 RMSE随快拍数的变化曲线(K=13)

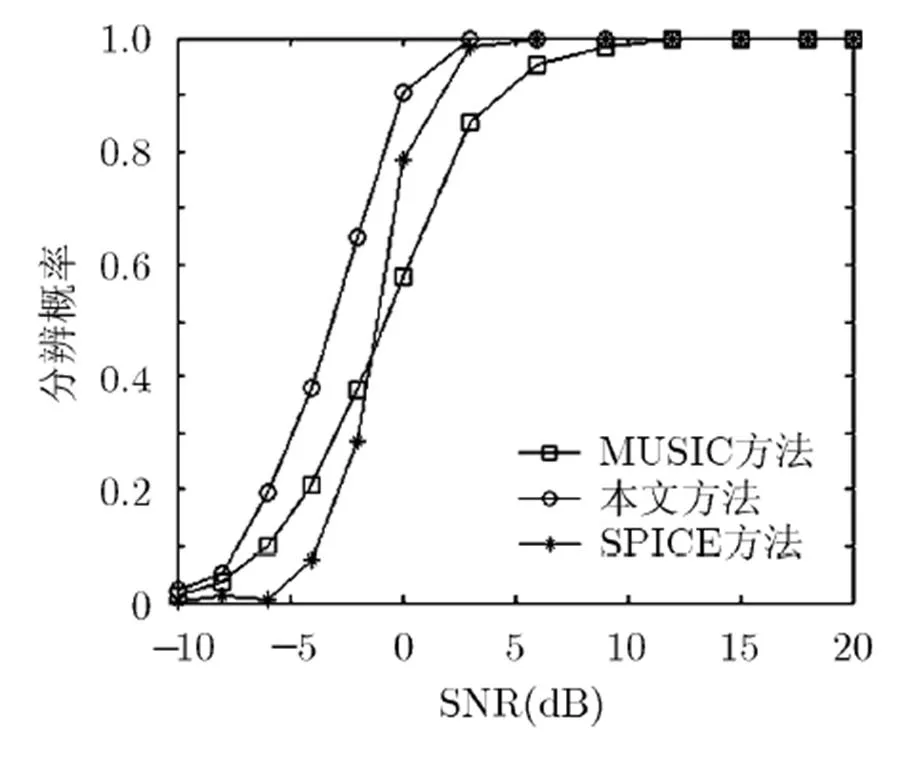
图11 角度分辨概率随SNR的变化曲线

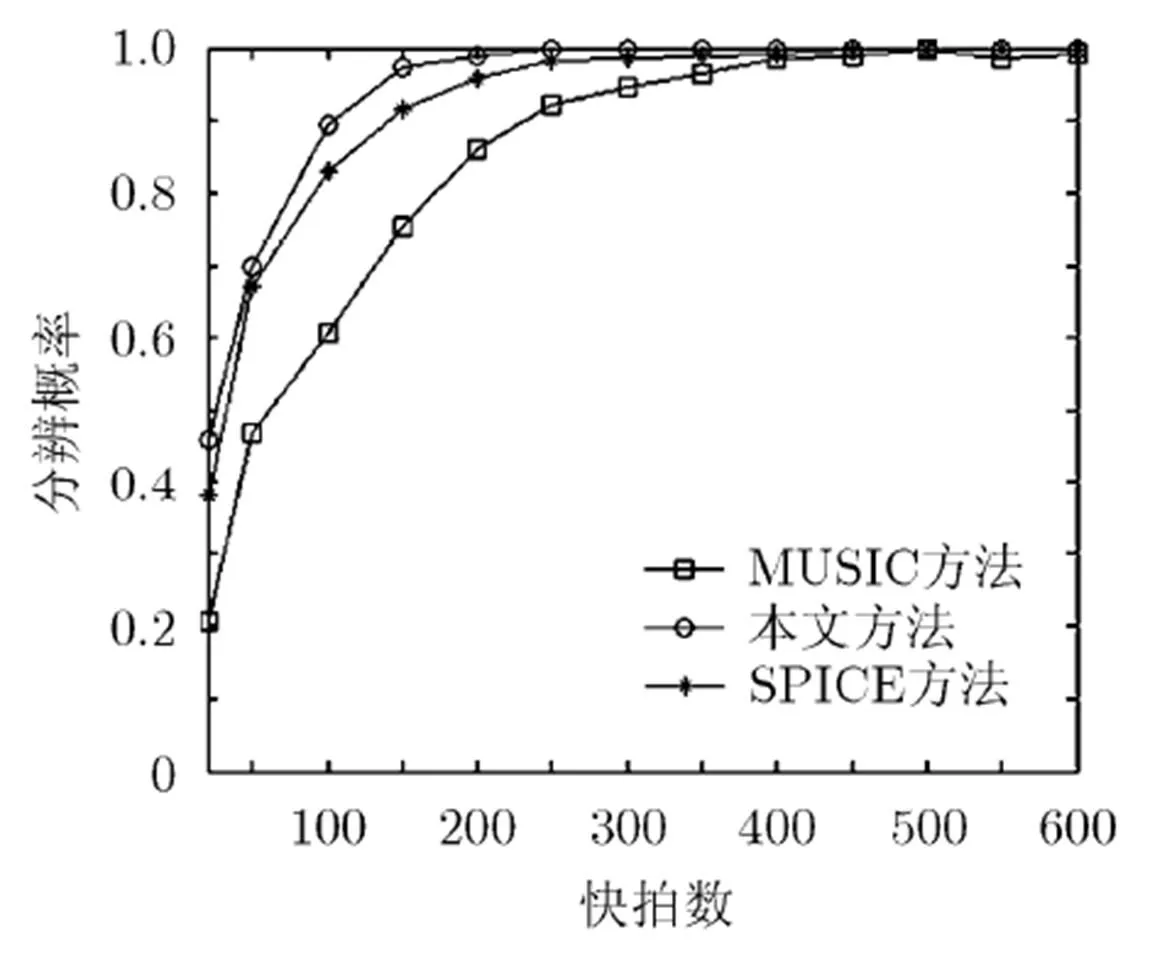
图12 角度分辨概率随快拍数的变化曲线

7 结束语

本文主要研究了两个方面的内容：(1)基于嵌套阵的自由度扩展特性提出一种MIMO雷达阵形设计新方法；(2)提出一种适用于嵌套MIMO雷达的改进稀疏DOA估计算法。仿真结果表明：(1)与具有相同收发阵元数目的传统MIMO雷达相比，嵌套MIMO雷达可有效提高MIMO雷达系统的自由度，解决传统MIMO雷达存在的欠定DOA估计问题；(2)本文提出的改进稀疏DOA估计算法具有比现有算法更优的角度估计性能。

[1] Fishler E, Haimovich A, Blum R,.. MIMO radar: an idea whose time has come[C]. Proceedings of the IEEE Radar Conference, Philadelphia, USA, 2004: 71-78.

[2] Li Jian, Stoica P, Xu Lu-zhou,.. On parameter identifiability of MIMO radar[J]., 2007, 14(12): 968-971.

[3] Bliss W and Forsythe W. MIMO radar and imaging: degrees of freedom and resolution[C]. Conference Record of the Thirty-Seventh Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, United States, 2003: 54-59.

[4] Ma Wing-kin, Hsieh Tsung-han, and Chi Chong-yung. DOA estimation of quasi-stationary signals with less sensors than sources and unknown spatial noise covariance: a khatri-rao subspace approach[J]., 2010, 58(4): 2168-2180.

[5] Pal Piya and Vaidyanathan P P. Nested arrays: a novel approach to array processing with enhanced degrees of freedom[J]., 2010, 58(8): 4167-4181.

[6] Pal Piya and Vaidyanathan P P. Nested arrays in two dimensions, Part I: geometrical considerations[J]., 2012, 60(9): 4694-4705.

[7] Pal Piya and Vaidyanathan P P. Nested arrays in two dimensions, Part II: application in two dimensional array processing[J]., 2012, 60(9): 4706-4718.

[8] Chen Chun-yang and Vaidyanathan P P. Minimum redundancy MIMO radars[C]. IEEE International Symposium on Circuits and Systems, Seattle, USA, 2008: 45-48.

[9] Stoica P, Babu P, and Li Jian. Spice: a sparse covariance-based estimation method for array processing[J]., 2011, 59(2): 629-638.

[10] 王凌, 李国林, 谢鑫, 等. 非圆信号二维DOA和初始相位联合估计方法[J]. 雷达学报, 2012, 1(1): 43-49.

Wang Ling, Li Guo-lin, Xie Xin,.. Joint 2-D DOA and noncircularity phase estimation method[J]., 2012, 1(1): 43-49.

[11] 朱莹, 张弓, 张劲东. 基于DCS的统计MIMO雷达信号模型及参数估计[J]. 雷达学报, 2012, 1(2): 143-148.

Zhu Ying, Zhang Gong, and Zhang Jin-dong. Signal model and parameters estimation of statistical MIMO radar based on distributed compressed sensing[J]., 2012, 1(2): 143-148.

[12] Yin Ji-hao and Chen Tian-qi. Direction-of-arrival estimation using a sparse representation of array covariance vectors[J]., 2011, 59(9): 4489-4493.

[13] Hu Nan, Ye Zhong-fu, Xu Xu,.. DOA estimation for sparse array via sparse signal reconstruction[J]., 2013, 49(2): 760-773.

[14] 王凌, 李国林, 谢鑫. 互耦效应下用单快拍数据实现相干信源完全解相干和解耦合[J]. 电子与信息学报, 2012, 34(10): 2532-2536.

Wang Ling, Li Guo-lin, and Xie Xin. Decorrelation and decoupling of coherent signals in the presense of mutual coupling using single snapshot[J].&, 2012, 34(10): 2532-2536.

[16] Malioutov D, Cetin M, and Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]., 2005, 53(8): 3010-3022.

[17] Ottersten B, Stoica P, and Roy R. Covariance matching estimation techniques for array signal processing applications[J]., 1998, 8(3): 185-210.

[18] Hu Nan, Ye Zhong-fu, Xu Dong-yang,.. A sparse recovery algorithm for DOA estimation using weighted subspace fitting[J]., 2012, 92(10): 2566-2570.

杨 杰： 男，1989年生，博士生，研究方向为MIMO雷达信号处理、阵列信号处理、稀疏谱估计.

廖桂生： 男，1963年生，教授，博士生导师，研究方向为阵列信号处理、空时自适应处理、动目标检测.

A Spatial Sparsity-based DOA EstimationMethod in Nested MIMO Radar

Yang Jie Liao Gui-sheng

(,,710071,)

The maximum number of targets that can be uniquely identified by the traditional MIMO radar is limited by the number of virtual sensors. To alleviate this issue, a novel antenna array in MIMO radar which is based on the concept of nested arrays is designed in this paper, and a modified spatial sparsity-based Direction-Of-Arrival (DOA) estimation method is proposed. First, the effect of nested sampling with application to virtual array of traditional MIMO radar on the DOA estimation performance is analyzed. Second, the method to design antenna array of nested MIMO radar is proposed. It is proven that nested MIMO radar can detect more targets than traditional MIMO radar when they share the same number of virtual sensors. Finally, a modified spatial sparsity-based approach to DOA estimation in nested MIMO radar is proposed based on noise subspace weighted minimization problem, which can increase resolution and effectively suppress spurious peaks. Extensive simulation results demonstrate the effectiveness and superiority of the proposed methods.

MIMO radar; Nested arrays; Direction-Of-Arrival (DOA); Spatial sparsity; Noise subspace weight

TN958

A

1009-5896(2014)11-2698-07

10.3724/SP.J.1146.2013.01900

杨杰 yangjie_xidian@126.com

2013-12-05收到，2014-04-11改回

国家自然科学基金(61231027)和国家973计划项目(2011CB707001)资助课题