一种具有恒虚警性质的检测跟踪联合处理算法

严俊坤 刘红亮 戴奉周 刘宏伟 罗 涛 保 铮



一种具有恒虚警性质的检测跟踪联合处理算法

严俊坤*刘红亮 戴奉周 刘宏伟 罗 涛 保 铮

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

该文提出一种具有恒虚警性质的检测跟踪联合处理算法。目的是在跟踪波门内平均虚警概率恒定的前提下，提升目标的平均检测概率和系统的跟踪性能。首先，该文结合跟踪器的反馈信息利用贝叶斯准则对传统的似然比检测器进行了修正，并给出了相应的判决表达式。而后，该文在给出了跟踪波门内平均检测概率和虚警概率的计算表达式。将其代入概率数据互联(PDA)算法互连概率的计算公式中，即可获取该算法的流程。最后，仿真实验验证了该算法的可行性和有效性。

目标跟踪；目标检测；概率数据互联；恒虚警率

1 引言

总的来说，上述算法将检测和跟踪过程进行了联合处理，有效提升了PDA算法的跟踪性能。但是，从原理上来讲，这些算法都通过提升虚警概率(降低检测门限)来提升性能。在这种情况下，当跟踪波门面积(体积或超体积)很大时，过检测门限的量测数量会很大，进而导致计算机过载。针对这个缺点，本文引入了波门内平均虚警概率的定义，提出了一种具有恒虚警性质的检测跟踪联合处理算法，简称JPDT-PDA(Joint Detection and Tracking Processing PDA)算法。与发射端的认知处理算法不同[12,13]，这种算法相当于是在雷达接收端的一种认知处理方式。目的是在波门内平均虚警率恒定的前提下，提升目标的平均检测概率和系统的跟踪性能。本文首先建立了密集杂波环境下目标跟踪的状态和观测模型；而后，本文将反馈的跟踪信息作为检测器的先验信息，在贝叶斯最小平均错误概率准则下给出了似然比检验的判决表达式，并推导了算法在跟踪波门内的平均检测概率和虚警概率。将其代入PDA算法互连概率的计算公式中，即可获取本文算法的流程。在结尾部分，本文从物理意义上解释了算法的原理，并验证了其有效性。

2 数学模型

2.1目标运动模型

假设一个目标在平面内做匀速运动，目标的运动方程可写为

2.2观测模型

本文假设虚警在整个波门内服从均匀分布[5]，因此有

3 经典PDA算法

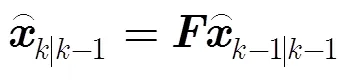
和真实新息协方差矩阵[7]：

总的来说，如图1所示，PDA算法利用目标前一时刻的状态估计及其运动模型确定目标预测点的位置，然后以预测点为中心建立跟踪波门。当跟踪门内有多个过门限的量测时，数据互联就是确定各个量测来源于目标的概率，并利用这些概率对新息进行加权以获得目标的状态估计。

图1 PDA算法一步预测和滤波示意图

4 JPDT-PDA算法

4.1 经典PDA算法的检测过程

4.2 JPDT-PDA算法的检测过程

根据贝叶斯最小平均错误概率准则[16]，似然比检验式可写为

这时，第个分辨单元在两种假设下的观测信号模型为

4.3 平均检测概率的计算

在JPDT-PDA算法的检测过程中，跟踪波门内各个分辨单元的检测门限是变化的，因此需要求取整个跟踪波门内的平均检测概率：

4.4平均虚警概率的计算

同理，波门内的平均虚警概率可计算为

5 实验结果分析

考虑了如下3组仿真参数：

3组参数中，初始SNR和虚警概率的设置不同。在初始SNR给定条件下，图3给出了平均SNR随帧号变化的关系。由图3可以发现，由于目标远离雷达飞行，平均SNR会随着时间的推移而降低。

为了更好地解释平均检测概率提升的原理，图5给出了不同工作参数下，JPDT-PDA算法和经典PDA算法在不同距离单元的检测门限(以某一帧为例)。由结果可以发现，经典PDA算法在不同距离单元的检测门限是相同的；JPDT-PDA算法利用跟踪过程反馈的信息，在整个波门内部检测门限设置的原则为：越靠近预测中心，检测门限越低；越远离预测中心，检测门限越高。因此，JPDT-PDA算法能在保证平均虚警概率相同的前提下，提升目标的平均检测概率。

图2 雷达与目标的空间位置关系

图3 平均SNR随帧号的变化情况

图4 检测概率

图5 检测门限

最后，为了验证本文算法的有效性，本文定义了如下两个性能指标：

从物理意义上解释，式(24)表示第次实验获取的目标平均跟踪误差大于观测提供的平均定位精度。

(2)目标的跟踪精度：用空间位置的均方根误差(RMSE)来描述(对未发散的航迹求统计平均)。

图6 算法的跟踪精度和航迹发散情况

6 结束语

本文结合跟踪器的反馈信息利用贝叶斯准则对传统的似然比检测器进行了修正，提出了一种具有恒虚警性质的JPDT-PDA算法。目的是在跟踪波门内平均虚警概率恒定的前提下，提升目标的平均检测概率和系统的跟踪性能。仿真实验表明，本文算法能有效提升目标的检测和跟踪性能。扩展实验表明，在本文算法中波门内的检测门限设置规则为：越靠近预测中心，检测门限越低；越远离预测中心，检测门限越高。在下一步工作研究中，我们会将本文的工作扩展至JPDA算法中，使其适用于多目标跟踪的情况。

[1] 谭顺成, 王国宏, 王娜, 等. 基于概率假设密度滤波和数据关联的脉冲多普勒雷达多目标跟踪算法[J]. 电子与信息学报, 2013, 35(11): 2700-2706.

[2] 欧阳成, 陈晓旭, 华云. 改进的最适高斯近似概率假设密度滤波[J]. 雷达学报, 2013, 2(2): 239-246.

[3] 吴伟, 尹成友. 一种用于多目标跟踪的增强型SMC-PHD滤波算法[J]. 雷达学报, 2012, 1(4): 406-413.

[4] Bar-Shalom Y and Tse E. Tracking and Data Association[M]. New York: Academic Press, 1988: 173-353.

[5] 韩崇昭, 朱洪艳, 段战胜, 等. 多源信息融合[M]. 北京: 清华大学出版社, 2006: 320-365.

[6] 刘宗香, 谢维信, 黄敬雄. 一种新的基于概率理论的概率数据互联滤波器[J]. 电子与信息学报, 2009, 31(7): 1641-1645.

[7] 程婷, 何子述, 李亚星. 一种具有自适应关联门的杂波中机动目标跟踪算法[J]. 电子与信息学报, 2012, 34(4): 865-870.

[8] Aslan M S and Saranl A. Threshold optimization for tracking a nonmaneuvering target[J]., 2011, 37(2): 2844-2859.

[9] Aslan M S and Saranl A. Advances in Heuristic Signal Processing and Applications[M]. Berlin Heidelberg: Springer, 2013: 111-143.

[10] Aslan M S, Saranl A, and Baykal B. Tracker-aware adaptive detection: an efficient closed-form solution for the Neyman- Pearson case[J]., 2010, 20(5): 1468-1481.

[11] Willett P, Niu R, and Bar-Shalom Y. Integration of Bayes detection with target tracking[J]., 2001, 49(1): 17-29.

[12] 严俊坤, 戴奉周, 秦童, 等. 一种针对目标三维跟踪的多基地雷达系统功率分配算法[J]. 电子与信息学报, 2013, 35(4): 901-907.

[13] 严俊坤, 纠博, 刘宏伟, 等. 一种针对多目标跟踪的多基雷达系统聚类与功率联合分配算法[J]. 电子与信息学报, 2013, 35(8): 1875-1881.

[14] Ristic B, Arulampalam S, and Gordon N. Beyond the Kalman Filter: Particle Filters for Tracking Applications[M]. Boston, MA: Artech House, 2004: 86-102.

[15] Liggins M E, Hall D L, and Llinas J. Handbook of Multisensor Data Fusion: Theory and Practice[M]. 2nd Ed. Boca Raton, CRC Press, 2009: 204-241.

[16] Kay S M. Fundamentals of Statistical Signal Processing: Estimation Theory[M]. 1st Ed. Upper Saddle River, Prentice-Hall, 1993: 295-345.

严俊坤： 男，1987年生，博士生，研究方向为认知雷达、目标跟踪与定位、协同探测.

刘红亮： 男，1989年生，博士生，研究方向为目标检测、目标跟踪与定位、协同探测.

戴奉周： 男，1978年生，博士，副教授，研究方向为统计与自适应信号处理及其在雷达信号处理和目标检测中的应用.

刘宏伟： 男，1971年生，博士，教授，博士生导师，研究方向为雷达系统、雷达信号处理、雷达自动目标识别等.

Joint Detection and Tracking Processing Algorithm with Constant False Alarm Rate Property

Yan Jun-kun Liu Hong-liang Dai Feng-zhou Liu Hong-wei Luo Tao Bao Zheng

(,,,710071,)

A joint detection and tracking processing algorithm is proposed in this paper with constant false alarm rate property. Under the precondition that the average false alarm rate of the gate is fixed, the aim is to improve the target detection probability as well as the tracking performance of the system. Firstly, according to the Bayes theory, the likelihood ratio detector is modified with the adoption of the feedback from the tracker. Then, the averaged detection probability and false alarm rate over the gate is derived. Substituting them into the calculation of the association probability of the Probabilistic Data Association (PDA) filter, the procedure of the proposed algorithm is obtained. Finally, the feasibility and validity of the algorithm are verified by the simulation results.

Target tracking; Target detection; Probabilistic Data Association (PDA); Constant false alarm rate

TN953

A

1009-5896(2014)11-2666-06

10.3724/SP.J.1146.2013.01925

严俊坤 jkyan@stu.xidian.edu.cn

2013-12-09收到，2014-05-26改回

国家自然科学基金(61201285, 61271291)，新世纪优秀人才支持计划(NCET-09-0630)和全国优秀博士学位论文作者专项资金(FANEDD-201156)资助课题