低复杂度的自适应置信差分迭代译码算法
段琳琳 王忠勇 王 玮 高向川 肖 岩
低复杂度的自适应置信差分迭代译码算法
段琳琳*①②王忠勇①王 玮①高向川①肖 岩①
①(郑州大学信息工程学院 郑州 450001)②(解放军信息工程大学信息系统工程学院 郑州 450001)
针对中短码长的低密度奇偶校验规则码(Low Density Parity Check, LDPC)规则码,该文采用消息更新规则改进和因子图变换方法,提出一种低复杂度差分迭代译码算法。在置信传播算法的基础上,仅当变量节点的消息值振荡时引入差分映射策略,得出一种选择性的置信差分规则,自适应地调整校验节点消息的归一化系数,提高译码性能。同时,采用展开校验节点的图变换方法,将计算复杂度从随节点度分布指数性增长降至线性增长。分别在高斯白噪声信道和瑞利衰落信道下进行仿真实验,结果表明该算法和基于图变换的其他低复杂度译码算法相比,性能优越且复杂度低,和对数似然比的置信传播算法(LLR-BP)相比,高信噪比区域内的性能优异,低信噪比区域内的计算复杂度明显降低。
低密度奇偶校验迭代译码算法;差分映射机制;因子图变换;自适应归一化系数
1 引言
基于因子图[1]的置信传播译码算法[2]具有计算并行化和延时短等优点,码长较长时性能可以逼近香农限,因此低密度奇偶校验(Low Density Parity Check, LDPC)码引起信道编码界和通信领域学者的关注和研究热潮。虽然长码性能优异,但实际应用中,在双向实时通信或对延时要求较高的环境下,显然不能满足延时要求。此时更适合采用中短码长的LDPC码,加之极大规模集成电路硬件实现技术的支持,码长度较短的规则LDPC码已经得到广泛应用[3]。
在中短码长的LDPC码图中存在短环、陷阱集和停止集[4,5],这些因素会引发迭代译码过程中某些变量节点的消息值即对数似然比外信息值(extrinsic Logarithm Likelihood Ratio, ex-LLR)的振荡现象[6],译码算法容易陷入陷阱集,出现错误平层,使译码性能受到损失。针对上述问题,文献[6]采用跟踪振荡现象和处理外信息值的方法对置信传播算法进行改进,将当前迭代与前次迭代的外信息值相加,减少振荡对译码性能的影响,所提出的算法和对数似然比的置信传播(Logarithm Likelihood Ratio BP, LLR-BP)算法相比性能略有提高。文献[7]侧重于解决陷阱集的问题,在分治(Divide and Concur, DC)算法[8]中引入差分动态机制,改进变量节点处的消息更新规则,提出了差分映射置信传播译码(Difference- Map Belief Propagation, DMBP)算法,它和置信传播(Belief Pro pagation, BP)算法、DC算法相比性能有所提高。均匀重加权置信传播(Uniformly ReWeighted Belief Propagation, URW-BP)算法[9]和变量因子出现概率置信传播(Variable Factor Appearance Probability Belief Propagation, VFAP-BP)算法[10]通过改进因子图中变量节点的消息更新规则和选取优化参数来提高译码性能。文献[11,12]在归一化的最小和算法基础上,根据迭代过程中校验节点的状态动态调整归一化系数,提出自适应归一化最小和算法,仿真结果表明,对于DVB-S2 LDPC长码,这种算法和归一化最小和算法(Min-Sum Algorithm, MSA)相比,该算法在增加少量计算复杂度的同时可提高性能。此外,还有采用多步骤量化消息[13]和期望传播[14]等方法降低错误平层和提高译码性能。
译码迭代过程中,并不是所有变量节点的信息值都会发生振荡。差分映射虽然是避免译码算法陷入陷阱集的一个有效策略,但如果对每个变量节点均使用差分映射更新消息,可能会因频繁过度的纠正而产生某些错误的软判决,并没有合理地发挥差分映射的优势。此外在对数概率测度下采用和积规则更新校验节点的消息,计算复杂度和节点度分布呈指数性增长关系,复杂度较高。因此本文提出一种低复杂的自适应置信差分传播算法,在置信传播算法的基础上,仅在变量节点消息值发生振荡时引入差分映射动态机制,进一步提高译码性能。同时,通过展开节点方法变换校验节点部分的因子图,借鉴归一化方法推导出一种自适应归一化的消息更新规则,复杂度和校验节点度分布的增长呈线性关系,复杂度大大降低。
2 变换校验节点因子图和改进消息更新规则
和Tanner因子图相比,Normal因子图[14]减少节点个数的同时突出地描述变量之间的函数约束关系,有助于描述分治和DMBP算法中的节点消息“复制”与“统一”的方法[7,8]。本文采用Normal因子图描述LDPC码,为比较低复杂的自适应置信差分传播算法和BP, DMBP等算法提供统一图模型,如图1所示。


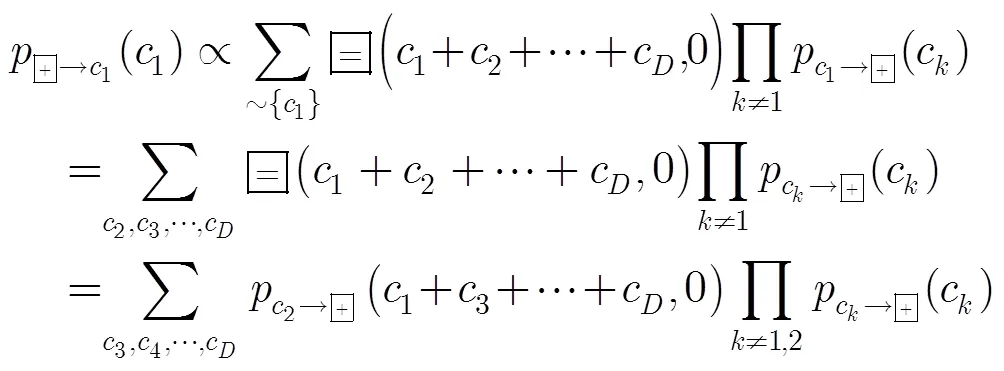
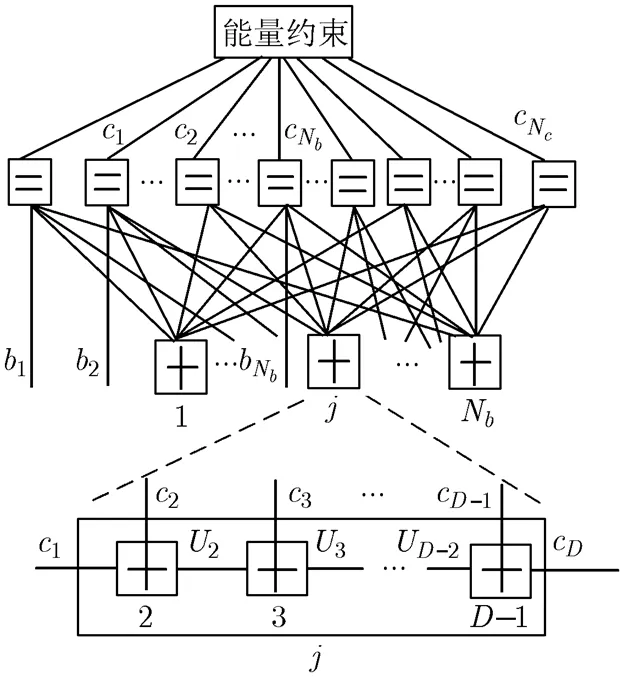
图1 LDPC码的正规因子图模型
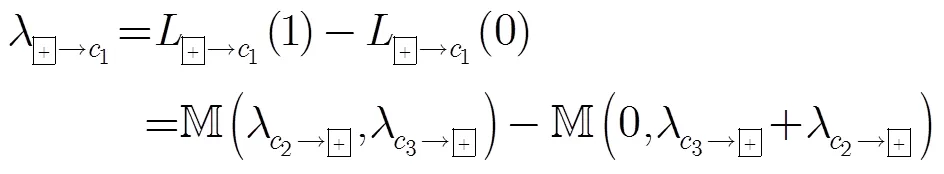

如果定义函数运算
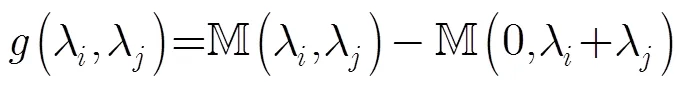
步骤1 更新前向和后向的内部消息
更新前向消息



同时,更新后向消息为



步骤2 更新校验节点到变量节点的消息

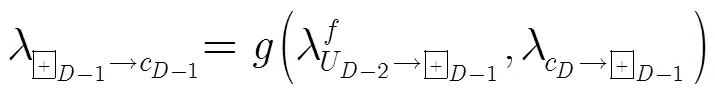
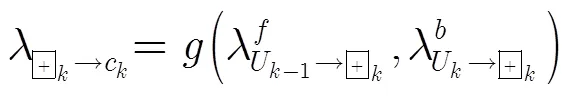
步骤3 判决并处理校验节点消息

3 改进变量节点的消息更新规则
LLR-BP算法[2]中更新变量节点到校验节点的消息
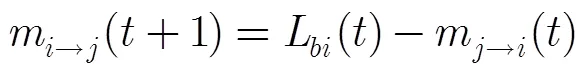
也称为BP规则,其中,变量节点的后验信息为

差分映射置信传播(DMBP)算法[7]中消息更新为

也称为DMBP规则,其中,变量节点后验信息为

在译码迭代过程中,振荡现象只发生在某些变量节点处[6]。如果仅采用BP规则,则没有考虑振荡和陷阱集对译码性能影响。如果仅采用DMBP规则,则对所有节点引入差分方法,虽然可以解决陷阱集问题,但同时也增加了计算量,甚至过度纠错会造成不必要的性能损失,从而减少译码性能提高的幅度。为进一步提高译码性能,本文从迭代过程中消息值的振荡现象入手,根据对数概率消息值测度下变量节点状态,选择性地采用两种规则更新变量节点消息,提出一种置信差分映射(Belief propagation and Difference-map, BD) 消息更新规则。仅当发生消息值振荡时,选择DMBP规则更新消息,否则仍保留BP规则。具体步骤为
步骤2 判断并选择更新规则:若
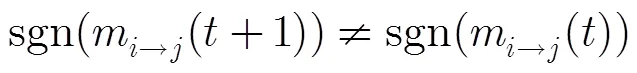
则用DMBP规则更新消息,也可以用式(18)和式(19)式得到的等价规则更新消息:
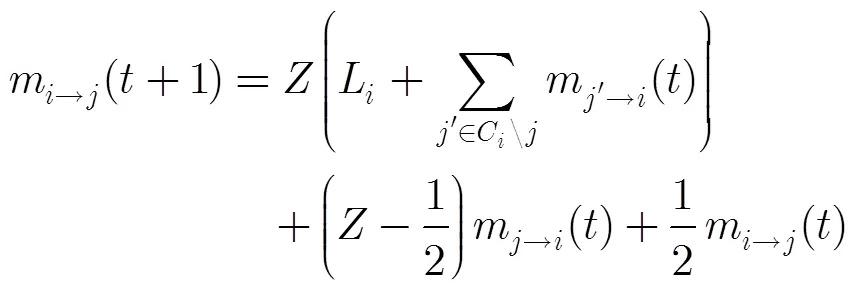
注意由式(16)和式(17)得到BP规则为
比较式(20)和式(21)可以看出,BP规则仅使用先验信息和当前迭代校验节点传给变量节点的外信息更新变量消息。而DMBP规则联合先验信息、当前迭代和前次迭代消息,取最优比例系数获得性能增益[7]。文献[7]中明确指出,分治算法中对所有信息比特信息之和取平均值。
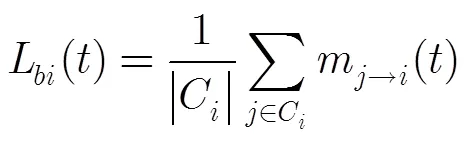


表1 3种消息更新规则的复杂度比较
4 改进的迭代译码算法及复杂度分析
基于上述对图与消息更新规则的改进,本文提出一种低复杂度的自适应置信差分迭代译码算法,(Adaptivly Normalized Low-Complexity Belief propagation and Difference-map, ANLC-BD)算法,具体步骤为:
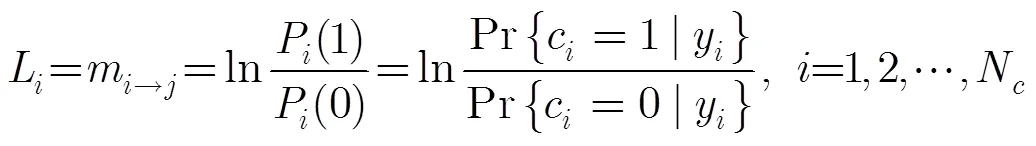
不同于ANLC-BD算法,LLR-BP算法在步骤2中按照式(3)更新校验节点消息,在步骤3中按照式(16)和式(17)更新变量节点消息。其他如低复杂度置信传播(Low Complexity-Belief Propagation, LC-BP)算法、低复杂度均匀重加权置信传播(Low Complexity-Uniformly ReWeighted belief propagation, LC-URW)算法、低复杂度差分映射置信传播(Low Complexity-Difference Map Belief Propagation, LC-DMBP)算法和低复杂度置信差分(Low Complexity-Belief propagation and Difference-map, LC-BD)算法是指在步骤2中均采用图变换方法,在步骤3中分别采用式(16)和式(17)的BP规则、URW-BP规则[9]、式(18)和式(19)的DMBP规则和本文提出的BD规则更新消息的译码算法。在LC-BP算法基础上再执行校验节点消息处理步骤,则构成自适应归一化的低复杂度置信传播(Adaptivly Normalized Low-Complexity Belief Propagation, ANLC-BP)算法。


5 仿真
在仿真中,选用8PSK格雷映射方式,码率为1/2的(1008,3,6)LDPC规则码,在AWGN信道和瑞利衰落信道下,对所提出的ANLC-BD算法进行性能仿真,=0.85,=0.75/0.85[11],=0.445[7]。同时给出用低复杂度自适应归一化规则改进的LLR-BP算法(称为ANLC-BP算法)的误码率特性曲线。LC-URW中仍取=0.55[9], LC-DMBP中仍取=0.445[7]。设最大迭代次数为100次。
首先,从图2中和图3的误码率特性曲线可以看出,AWGN和瑞利衰落信道下,低信噪比区域内,ANLC-BD算法的性能均逼近LLR-BP算法。高信噪比区域内,AWGN信道下的ANLC-BD算法均优于LLR-BP和BP算法,但和最大似然比译码算法(Maximum Likelihood Decoding, MLD)之间仍存在性能差异,瑞利衰落信道下的ANLC-BD算法和LLR-BP算法相比略有性能增益。和LC-BP算法相比,LC-URW和LC-DMBP依次提高译码性能。仅采用BD规则的LC-BD算法和仅处理校验节点消息的ANLC-BP算法均可以进一步提高译码性能。ANLC-BD算法结合两者优势,获得是最大的性能增益。

综合图2至图5的结果,在低信噪比区域,本文所提出的ANLC-BD算法和LLR-BP算法性能相当,复杂度降低;高信噪比区域内,复杂度相当,性能略有提高。在上述低复杂译码算法中,仅处理校验节点消息的ANLC-BP算法和仅改进变量节点更新规则的LC-BD算法均提高译码性能,同时都可以减少实际总迭代次数,ANLC-BD算法结合两者优势,获得是最大的性能增益和最少的实际总迭代次数。
最后,在AWGN信道各信噪比下,以及瑞利衰落信道E/0=6.5 dB下,仿真本文所提算法取不同值时的性能,图6结果表明,各种信噪比下均存在=0.445使性能最优。

图2 AWGN信道下,ANLC-BD算法和其他改进算法的性能比较

图3 瑞利衰落信道下,ANLC-BD算法和其他改进算法的性能比较

图4 AWGN信道下,ANLC-BD算法和其他改进算法的迭代次数比较

图6 AWGN和瑞利衰落信道下,Z的不同取值对ANLC-BD算法性能的影响
6 结束语
本文采用因子图中图变换和规则改进两类方法,提出一种低复杂度的自适应置信差分译码算法。和LLR-BP算法相比,两种更新规则的引入实质上是进行了三方面的改进,包括校验节点的图变换和相应更新规则、处理校验节点消息以及变量节点更新规则。上述改进方法的结合带来优势有两点,一是综合图变换方法可以降低每次迭代复杂度和后两方面改进均可以减少实际总迭代次数的特点,降低了算法在低信噪比区域的整体计算复杂度。二是综合了处理校验节点信息和变量节点更新规则均能提高性能的特点,提高整体算法高信噪比区域的性能。仿真结果表明,在AWGN信道和瑞利衰落信道下,本文所提算法和置信传播算法相比,低信噪比区域内性能相当,复杂度较低,高信噪区域内复杂度相当,性能优越。同时性能明显优于低复杂度BP, DMBP和URW-BP译码算法。本文提出的方法可以扩展至长码、多元或不规则码等译码算法中。
[1] Loeliger H A. An introduction to factor graphs[J]., 2004, 21(1): 28-41.
[2] Chen Jinghu and Fossorier M P C. Near optimum universal belief propagation based decoding of low-density parity check codes[J]., 2002, 50(3): 406-414.
[3] Hu Zi-xia and Liu Hui. A low-complexity LDPC decoding algorithm for hierarchical broadcasting: design and implementation[J]., 2013, 62(4): 1843-1849.
[4] Laendner S and Milenkovic O. LDPC codes based on latin squares: cycle structure, stopping set, and trapping set analysis[J]., 2007, 55(2): 303-312.
[5] Milenkovic O, Soljanin E, and Whiting P. Asymptotic spectra of trapping sets in regular and irregular LDPC code ensembles[J]., 2007, 53(1): 39-55.
[6] Gounai S, Ohtsuki T, and Kaneko T. Modified belief propagation decoding algorithm for low-density parity check code based on oscillation[C]. Proceedings of the IEEE 63rd Vehicular Technology Conference,Melbourne vic, 2006, 3: 1467-1471.
[7] Yedidia J S, Wang Yige, and Draper S C. Divide and concur and difference-map BP decoders for LDPC codes[J]., 2011, 57(2): 786-802.
[8] Gravel S and Elser V. Divide and concur: a general approach to constraint satisfaction[J]., 2008, 78(3): 1-4.
[9] Wymeersch H, Penna F, and Savic V. Uniformly reweighted belief propagation for estimation and detection in wireless networks[J]., 2012, 11(4): 1587-1595.
[10] Liu Jing-jing and de Lamare R C. Low-latency reweighted belief propagation decoding for LDPC codes[J]., 2012, 16(10): 1660-1663.
[11] Wu Xiao-fu, Song Yue, Jiang Ming,.. Adaptive- normalized/ offset min-sum algorithm[J]., 2010, 14(7): 667-669.
[12] Fan Li-wen, Pan Chang-yong, Peng Ke-wu,.. Adaptive normalized min-sum algorithm for LDPC decoding[C]. 2013 9th International Wireless Communications and Mobile Computing Conference (IWCMC), Sardinia, Italy, 2013: 1081-1084.
[13] Tolouei S and Banihashemi A H. Lowering the error floor of LDPC codes using multi-step quantization[J]., 2014, 18(1): 86-89.
[14] Loeliger H A, Dauwels J, Hu Jun-li,.. The factor graph approach to model-based signal processing[J]., 2007, 95(6): 1295-1322.
[15] Henk W. Iterative Receiver Design[M]. Cambridge: Cambridge University Press, 2007: 153-154.
段琳琳: 女,1974年生,博士生,研究方向为基于图模型的无线通信信号处理.
王忠勇: 男,1965年生,教授,研究方向为无线通信、数字通信和嵌入式系统.
王 玮: 女,1974年生,博士生,研究方向为信号处理.
高向川: 男,1981年生,博士,研究方向为3G&4G无线通信、信号处理、干扰对齐技术.
肖 岩: 男,1978年生,博士生,研究方向为无线通信信号处理.
An Adaptive Belief Propagation Difference-map Iterative Decoding Algorithm with Low Complexity
Duan Lin-lin①②Wang Zhong-yong①Wang Wei①Gao Xiang-chuan①Xiao Yan①
①(,,450001,)②(,,450001,)
In this paper, an adaptive belief difference-map propagation algorithm with low complexity is proposed for short and middle length LDPC regular codes by modifying message update rules and transforming factor graph. To improve decoding performance, a new selective belief propagation difference-map message update rule is introduced by borrowing the difference-map strategy for variable node messages oscillation, and the normalized factor is adjusted adaptively. Meanwhile, the computational complexity exponential in the degree of check node is decreased into linear in degree by opening the check node. The simulation results illustrate that the proposed algorithm has better performance and lower complexity than other iterative decoding algorithms based on the modified factor graphs. Compared to the LLR-BP, it better performance at high/0and the computational complexity is apparently downgraded at low/0.
LDPC iterative decoding algorithm; Difference-Map (DM) strategy; Transforming factor graph; Adaptive normalized factor
TN911.23
A
1009-5896(2014)11-2640-06
10.3724/SP.J.1146.2014.00234
段琳琳 llduan@126.com
2014-02-24收到,2104-06-26改回
国家自然科学基金(61172086, 61201251),国家自然科学基金联合基金(U1204607)和博士后科研启动基金(2011012)资助课题

