面向物理层安全的一种打孔极化编码方法

易 鸣 季新生 黄开枝 金 梁 王 婧



面向物理层安全的一种打孔极化编码方法

易 鸣*①②季新生①②黄开枝①②金 梁①②王 婧②

①(国家数字交换系统工程技术研究中心 郑州 450002)②(解放军信息工程大学 郑州 450002)

为了解决物理层安全编码中安全性和可靠性之间的矛盾和提高保密速率，该文提出一种基于打孔极化码的安全编码方法。根据信道极化理论，该方法将私密信息位映射到合法者正常接收而窃听者无法译码的特定逻辑信道输入位，保证私密信息可靠且安全传输。然后，通过分析极化码的校验关系树，利用3个参数表征输出节点对私密信息位的影响，再按照影响程度大小确定打孔位置。理论分析与仿真结果表明，该方法保证私密信息传输安全性和可靠性的同时，提高了私密信息传输的有效性。

无线通信；物理层安全；安全编码；极化码；打孔

1 引言

无线物理层安全编码是一种在保证授权双方信息传输可靠性的基础上，进一步考虑信息传输安全性的信道编码技术。其目的是在通信双方不事先获取密钥的前提下使得授权双方的私密信息能够正常传输，而不被第三方窃听。

现有安全编码可以分为3类：第1类，首先利用相关方法实现合法信道近似无噪传输，然后利用安全编码实现私密信息的安全传输。例如文献[1]首先利用交替反馈使合法信道基本无噪，然后利用陪集编码[2]保证安全传输，随着合法信道质量变差，其信息交互量也会随之增大。还可以利用人工噪声机制[3]，恶化窃听信道的同时保证合法信道能够正常接收，然后利用低密度奇偶校验码进行陪集编码[4]，但是这种人工噪声方法，可以被窃听者多天线破解[5]。第2类，安全编码同时保证安全和可靠传输。例如文献[6]将陪集编码和纠错码级联，具有较好的纠错能力，但安全性能很差；文献[7, 8]将陪集的概念扩展到格码，但在维数较高时实现复杂度非常大；文献[9-11]在具有良好纠错性能的母码基础上，不传私密信息或者加入随机扰乱；文献[12]从调制映射的角度，设计了一种反格雷码。这类方法的最大缺点是，它们在提高窃听方接收比特错误率(Bit Error Rate, BER)时，必然会恶化合法接收者性能。第3类，将码字结构与信道实时特征进行联合设计，实现合法接收端码域内信息不变，而窃听端码域内信息随机变化。例如文献[13]提出的一种基于信道特征随机投影的物理层安全编码方式，文献[14]提出的一种分布式天线跳空收发技术，它们都需要精确知道每个传输时刻的信道状态信息。

2009年，文献[15]提出了基于信道极化的编码理论。与上述3类方法相比，利用信道极化进行安全编码有如下优点：(1)它的安全源自信道间自身的噪声差异，而不是可以通过多天线技术消除的人工噪声；(2)它在安全传输的同时不会恶化合法接收端的BER; (3)它只需要信道的统计状态信息，而不需要精确知道每个传输时刻的相位幅度信息。但是现有文献仅对无限码长时的极化安全码性能进行了理论限分析，并没有给出极化安全码参数的具体设置方法[16,17]。另外，极化码的码长一定是2的幂次方，传输效率较低[18]。在收发双方只使用一对编译码器时，提高信息传输效率的一种方法是在编码器输出端进行码字打孔传输，但是传统极化码打孔方案没有考虑输出节点对特定私密信息输入位的影响程度[19,20]，打孔性能较差。

2 相关概念和问题描述

假设合法信道、窃听信道均为二进制输入对称信道(Binary Symmetric Channel, BSC)，发送者(Alice)希望合法接收者(Bob)能够正常恢复私密信息，同时不希望窃听者(Eve)获得任何私密信息。

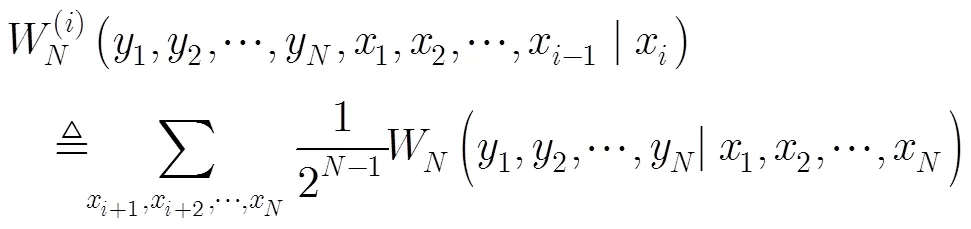
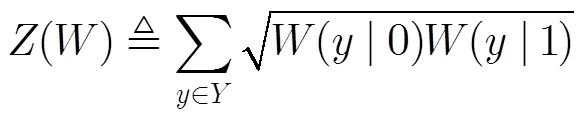
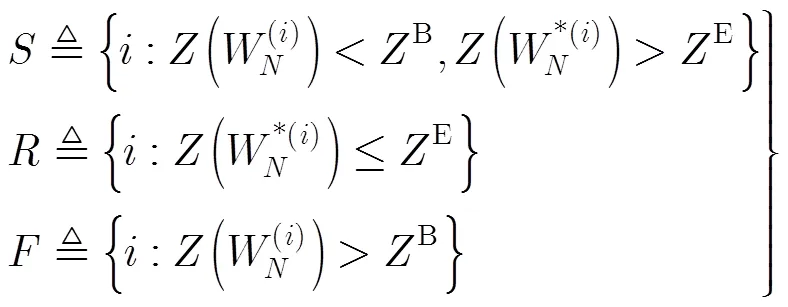
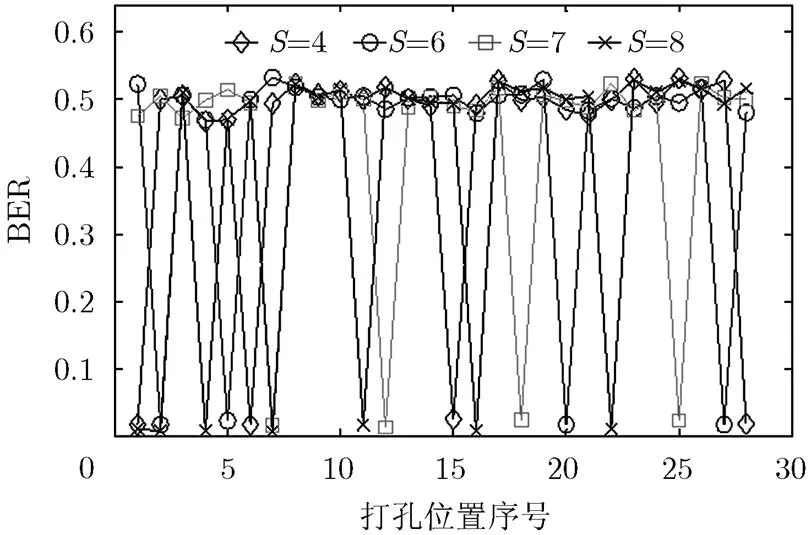
图1 打孔位置对输入信息BER的影响图

3 基于极化码打孔的安全编码方法

基于极化码打孔的安全编码方法，首先需要根据信道统计信息和系统的可靠性、安全性要求，确定安全极化母码的参数。然后构造母码的校验关系网，得到输出节点对每个私密信息位的影响程度表达式，并按照重要程度和相互关系确定非打孔节点集合。

3.1 安全极化母码的设计

证毕

算法1 确定安全极化母码参数

3.2 打孔方案设计

下面基于极化码的校验关系，分析极化码不同输出节点对特定私密信息位的影响程度和相互关系。

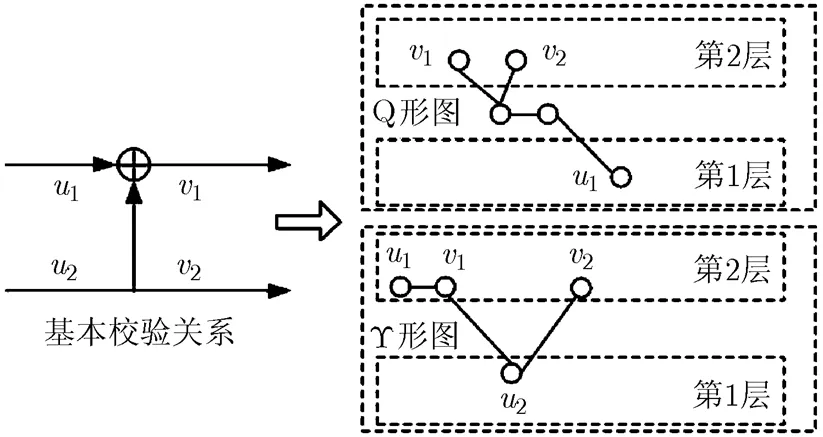
图2 极化码基本校验关系树

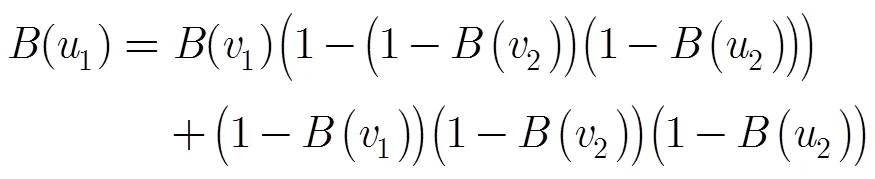
根据文献[22]中的统一编解码与校验信息传递理论，可将式(5)和式(6)写为

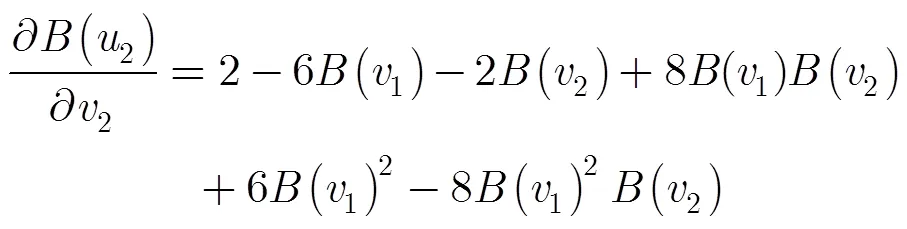
将定理2的结论简记为逻辑关系式(12)和式(13)：

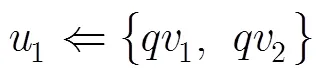
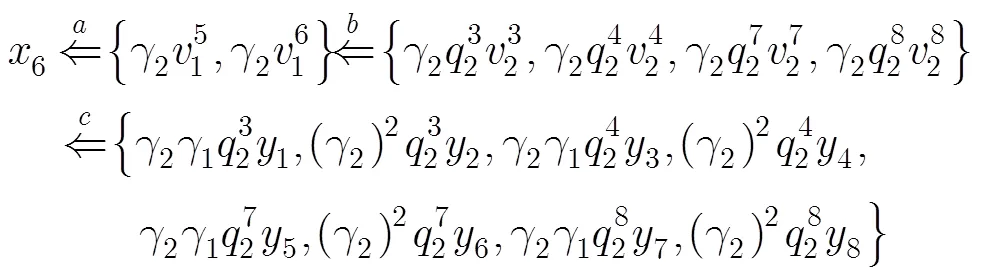
根据极化码对称性质可知，输出位对输入节点的影响程度可能包含3个参数：

图3 校验关系网示例

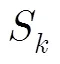
算法2 安全极化码打孔方案

步骤3 确定全体输出节点对私密信息位的影响程度表达式(14)；

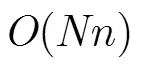
4 典型结果及性能仿真

表1 算法1的部分结果

图4给出了不同窃听信道转移概率下，逻辑信道序号对应的信息输入属性分别为私密信息或随机信息，空白部分表示该逻辑信道序号对应固定信息输入位置。从图4中可以看出，窃听信道转移概率高的随机信息输入位置一定包含在窃听信道转移概率低的随机信息输入位置中，这是由于信道质量的的“好”逻辑信道一定包含在信道质量高的“好”逻辑信道中，这也验证了文献[16]定理4的结论。但是私密信息输入位置没有明确的包含关系，这是由于私密信息输入位置需要同时考虑窃听信道和合法信道。

当合法信道的转移概率为0.01，窃听信道的转移概率为0.15时，首先根据算法1确定安全极化母码参数，然后根据算法2确定输出端的打孔位置。此处仅给出打孔位数为23时的最优打孔位置{1,2,5,9,17,33,129,257,385,513,514,515,516,517,521,529,545,577,641,769,771,777,897}，其他结果如图5所示。

图6对比分析了本文方法与文献[19]和文献[20]的打孔方案，当合法信道的转移概率为0.01，窃听信道的转移概率为0.15时，合法接收者和窃听者的BER随打孔数量的变化示意图。

图4 安全极化母码的私密信息和随机信息输入位置图

图5 不同打孔数下的打孔位置图

图6 不同打孔方案性能对比图

5 结束语

安全性需要提高接收端的BER，可靠性需要降低接收端的BER，有效性需要减少码字冗余，解决这些问题的一种有效途径是，将信道质量的差异转移到特定比特的BER差异，然后进行打孔传输。本文根据信道极化理论，提出了一种基于打孔极化码的安全编码方法，在编码器输入端选择特定的位置映射为私密信息保证安全性和可靠性，同时在输出端优化打孔方案提高信息传输速率。由于极化编码具有很强的对称性和迭代计算的优势，下一步有必要利用这些特点，进一步降低所提打孔方法的计算复杂度。

[1] Wen H, Ho P H, and Jiang X H. On achieving unconditional secure communications over binary symmetric channels(BSC)[J]., 2012, 1(2): 49-52.

[2] Ozarow L H and Wyner A D. Wire-tap channelⅡ[J]., 1984, 63(10): 2135-2137.

[3] Liao W, Chang T, Ma W,QoS-based transmit beamforming in the presence of eavesdroppers: an optimized artificial noise aided approach[J]., 2011, 59(3): 1202-1216.

[4] Tangaraj A, Dihidar S, and Calderbank A R. Applications of LDPC codes to the wire-tap channel[J]., 2007, 53(8): 2933-2945.

[5] 吴飞龙, 王文杰, 王慧明, 等. 基于空域加扰的保密无线通信统一数学模型及其窃密方法[J]. 中国科学：信息科学, 2012, 42(4): 483-492.

Wu Fei-long, Wang Wen-jie, Wang Hui-ming,A unified mathematical model for spatial scrambling based secure wireless communication and its wiretap method[J]., 2012, 42(4): 483-492.

[6] Cassuto Y and Bandic Z. Low-complexity wiretap codes with security and error-correction guarantees[C]. Proceedings of IEEE Information Theory Workshop, Dublin, Ireland, 2010: 1-5.

[7] Belfiore J C and Oggier F. Lattice codes design for the Rayleigh fading wire-tap channel[C]. Proceedings of IEEE International Conference on Communications Workshops, Kyoto, Japan, 2011: 1-5.

[8] Lin F C and Oggier F. A classification of unimodular lattice wiretap codes in small dimensions[J]., 2013, 59(6): 3295-3303.

[9] Maturo N, Baldi M, Bianchi M,Security gap performance of some LDPC code constructions[C]. Proceedings of 36th International Conference on Telecommunications and Signal Processing, Rome, Italy, 2013: 77-81.

[10] 钟州, 金梁, 黄开枝, 等. 基于二维修正减小LDPC码安全间隙的译码算法[J]. 电子与信息学报, 2013, 35(8): 1946-1951.

Zhong Zhou, Jin Liang, Huang Kai-zhi,Decoding algorithm for reducing security gap of LDPC codes based on two-dimensional information correction[J].&, 2013, 35(8): 1946-1951.

[11] Baldi M, Bianchi M, and Chiaraluce F. Coding with scrambling, concatenation, and HARQ for the AWGN wire-tap channel: a security gap analysis[J]., 2012, 7(3): 883-894.

[12] Kwark B J, Song N K, Park B,Physical layer security with Yarg Code[C]. Proceedings of IEEE International Conference on Emerging Network Intelligence, Sliema, Malta, 2009: 43-48.

[13] 王亚东, 黄开枝, 吉江. 一种多天线信道特征投影物理层安全编码算法[J]. 电子与信息学报, 2012, 34(7): 1653-1658.

Wang Ya-dong, Huang Kai-zhi, and Ji Jiang. A physical layer secrecy coding algorithm using multi-antenna channel characteristics projection[J].&, 2012, 34(7): 1653-1658.

[14] 殷勤业, 贾曙乔, 左莎琳, 等. 分布式多天线跳空收发技术(I)[J]. 西安交通大学学报, 2013, 47(1): 1-8.

Yin Qin-ye, Jia Shu-qiao, Zuo Sha-lin,A distributed multi antenna space hopping transceiver technique (Ⅰ)[J]., 2013, 47(1): 1-8.

[15] Arikan E. Channel polarization: a method for constructing capacity-achieving codes for symmetry binary-input memoryless channels[J]., 2009, 55(7): 3051-3073.

[16] Mahdavifar H and Vardy A. Achieving the secrecy capacity of wiretap channels using polar codes[J]., 2011, 57(10): 6428-6443.

[17] Andersson M. Coding for the wiretap channel[D]. [Ph.D. dissertation], Sweden, School of Electrical Engineering Royal Institute of Technology, 2011.

[18] Tal I and Vardy A. How to construct polar codes[J]., 2013, 59(10): 6562-6582.

[19] Niu K, Chen K, and Lin J R. Beyond turbo codes: rate-compatible punctured polar codes[C]. Proceedings of IEEE International Communication on Communications, Budapest, Hungary, 2013: 3423-3427.

[20] Eslami A and Pishro-Nik. A practical approach to polar codes[C]. Proceedings of IEEE International Symposium on Information Theory, St. Petersburg, Russia, 2011: 16-20.

[21] 贺鹤云. LDPC码基础与应用[M]. 北京: 人民邮电出版社, 2009: 122-130.

He He-yun. Principle and Application of LDPC[M]. Beijing: Posts & Telecom Press, 2009: 122-130.

[22] 吴湛击. 现代纠错编码与调制理论及应用[M]. 北京：人民邮电出版社, 2008: 252-260.

Wu Zhan-ji. Modern Channel Coding and Modulation: Theory and Application[M]. Beijing: Posts & Telecom Press, 2008: 252-260.

[23] Yuan B and Parhi K K. Architecture optimizations for BP Polar decodes[C]. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, Canada, 2013: 2654-2658.

[24] Arıkan E and Telatar E. On the rate of channel polarization[C]. Proceedings of IEEE International Symposium on Information Theory, Seoul, South Korea, 2009: 1493-1495.

易 鸣： 男，1986年生，博士生，研究方向为物理层安全编码.

季新生： 男，1968年生，教授，博士生导师，研究方向为信息安全.

黄开枝： 女，1973年生，教授，硕士生导师，研究方向为无线通信安全.

A Method Based on Puncturing Polar Codes for Physical Layer Security

Yi Ming①②Ji Xin-sheng①②Huang Kai-zhi①②Jin Liang①②Wang Jing②

①(,450002,)②(,450002,)

To solve the confliction between the security and reliability of physical layer security codes and improve the secrecy rate, a security coding method based on puncturing polar codes is proposed. In order to keep the security and reliability, the confidential information is mapped to the specific input proposition which could be decoded by legal receiver but be equivocal for eavesdropper based on channel polarization theory. By analyzing the check trees of polar codes, the puncturing pattern is designed based on the influences of outputs on confidential information which are described by three parameters. The theoretical analysis and simulation results verify that the proposed method is able to guarantee simultaneously the security and reliability while improving the efficiency of the confidential information.

Wireless communication; Physical layer security; Security coding; Polar codes; Puncture

TN929.53

A

1009-5896(2014)12-2835-07

10.3724/SP.J.1146.2014.00013

易鸣 ymwlcaq@gmail.com

2014-01-03收到，2014-03-05改回

国家自然科学基金(61171108, 61379006)资助课题