带丁坝型半封闭矩形海湾中M2分潮潮波和潮流特性分析

钱学生，陈永平*，张长宽

（1.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098；2.河海大学港口海岸与近海工程学院，江苏南京 210098）

带丁坝型半封闭矩形海湾中M2分潮潮波和潮流特性分析

钱学生1，2，陈永平1，2*，张长宽2

（1.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098；2.河海大学港口海岸与近海工程学院，江苏南京 210098）

将黄渤海海域概化为矩形海湾，山东半岛概化为垂直于海岸的巨型丁坝，形成一个带丁坝型半封闭矩形海湾。利用DELFT3D-FLOW计算模块在上述海湾中进行了M2分潮数值模拟，对其无潮点和辐射状潮流场的特性进行了分析。研究发现：考虑科氏力影响和巨型丁坝反射作用，坝前形成了明显的无潮点，但在等水深条件下并未形成辐射状潮流场，而叠加上倾斜海底地形后其得以形成；无潮点和辐射状潮流场顶端位置受水深影响明显，随着平均水深的增大，无潮点将向湾口和湾中轴线方向偏移，而辐射状潮流场顶端则向湾口方向偏移。研究结果有助于加深对带丁坝型半封闭矩形海湾中驻潮波系统形成机制和动力特性的理解和认识。

带丁坝型矩形海湾；M2分潮；驻潮波；无潮点；辐射状潮流场

1 引言

南黄海位于山东半岛成山角与朝鲜半岛长山连线以南，长江口北岸启东嘴与济州岛西南角连线以北。许多学者通过实测资料分析［1－2］和二、三维数值模拟［3－10］，研究了渤、黄、东海潮波和潮流的运动特性和时空分布特征，其中南黄海驻潮波系统的形成是其重要特征之一［11］。关于南黄海驻潮波系统的成因，前人已做出如下解释：东海前进潮波进入黄海海域时遇到山东半岛基岩古陆而发生部分反射，在地球自转效应下形成逆时针旋转潮波，该旋转潮波与后继前进潮波相遇，在南黄海海域形成一支独立的驻潮波系统，海州湾附近的无潮点是其波节点，而波腹大致位于苏北弶港岸外的辐射沙脊区［12－14］。

自从Taylor提出矩形海湾问题［15］以来，已有学者分别从海底摩擦［16－18］、海底地形［19－23］和湾顶潮能逸出［24－25］等角度对湾内无潮点或圆流点的位置分布做了大量的分析工作。为了更加深刻地掌握南黄海潮波特性，也有部分学者［24－27］曾将南黄海概化为一个巨大的矩形海湾加以研究。就其中的驻潮波而言，有学者指出海底地形的变化将使该潮波系统中的无潮点位置发生偏移，但他们没有给出具体的成因解释。此外，辐射状潮流场是南黄海驻潮波最具典型的水动力特征之一，在以往对矩形海湾的研究中很少以辐射状潮流场为着眼点，来探讨其形成机制及其动力特征。

针对以上问题，本文将黄、渤海海域概化为矩形海湾，山东半岛概化为垂直于海岸的巨型丁坝，形成一个带丁坝型半封闭矩形海湾（图1）。利用DELFT3D-FLOW计算模块建立了一个二维潮流数学模型，采用等深条件下矩形海湾M2分潮的解析结果［28］对模型进行了验证，在此基础上，通过数值实验研究了巨型丁坝和不同水下地形对驻潮波的影响，并就无潮点位置和辐射状流场特性进行了定量分析。

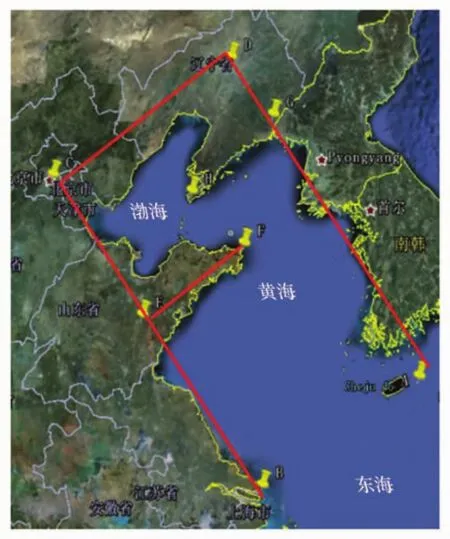
图1 黄、渤海海域概化图Fig.1 Schematic domain of the Yellow Sea and the Bohai Sea

2 数学模型的建立

2.1 基本方程

DELFT3D-FLOW计算模块采用基于曲线网格下的二维非线性浅水方程来进行潮波和潮流数值计算，其基本方程可描述为：

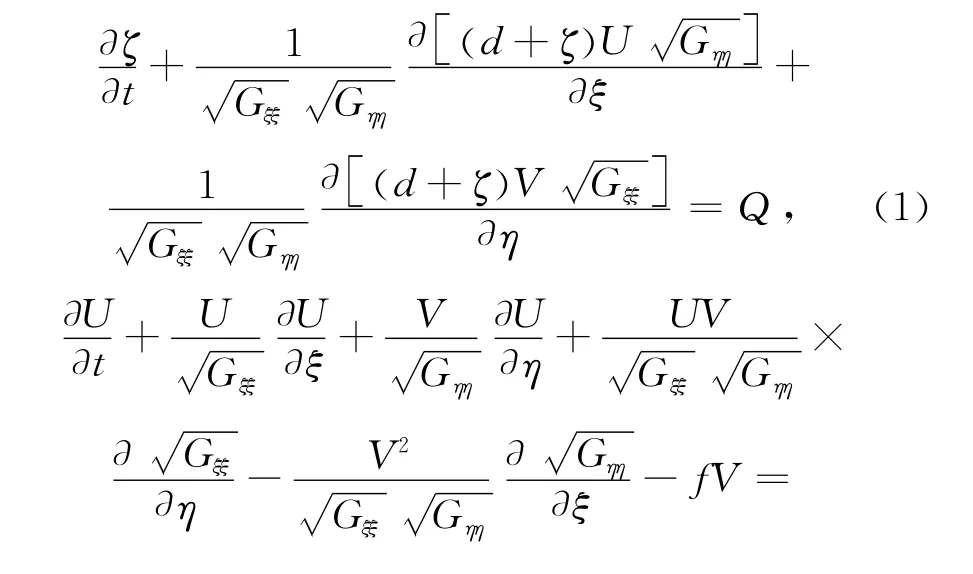
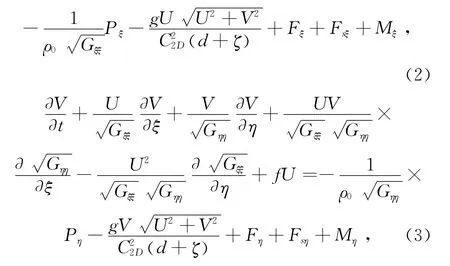
2.2 参数设置

本次计算的矩形区域长1 000 km，宽500 km，丁坝长300 km，距离湾口450 km。网格步长设定为2 000 m×2 000 m，时间步长为1 min。为了与解析结果［28］进行对比，水平涡黏系数设为0，谢才系数取为50.6。

2.3 初边值条件

在开边界（湾口位置）每10 km一个点处，给定历时1个月的水位过程（时间间隔15 min）边界条件，其量值由解析结果给出；在闭边界处（湾壁位置）采用不可入边界条件。本模型采用冷启动方式计算，计算历时1个月。

3 模型验证

为检验本模型的合理性，首先对等水深条件下（水深h＝68.4 m）矩形海域的M2分潮进行了数值计算，然后与相对应的解析结果进行对比（见图2）。其中，图2a为潮位同潮图对比结果，而图2b为t＝0.147 14T时刻（T为一个潮周期）的流场图对比结果，图中红线（流矢）代表解析解结果，而蓝线（流矢）代表数值解结果。需要指出的是，受求解方法的限制，本解析解忽略了对流项和扩散项的影响，且底部摩擦与流速的一次方成正比。

从图2中可以看出，数值解与解析解结果总体吻合良好。由于解析解中摩擦项取为与流速的一次方成比例，而数值解中摩擦项取为与流速的二次方成比例，即数值解考虑了摩擦效应的非线性作用，这可能是导致计算结果的同潮时线滞后于解析解同潮时线 和其流速值小于解析条件下流速结果的主要原因。

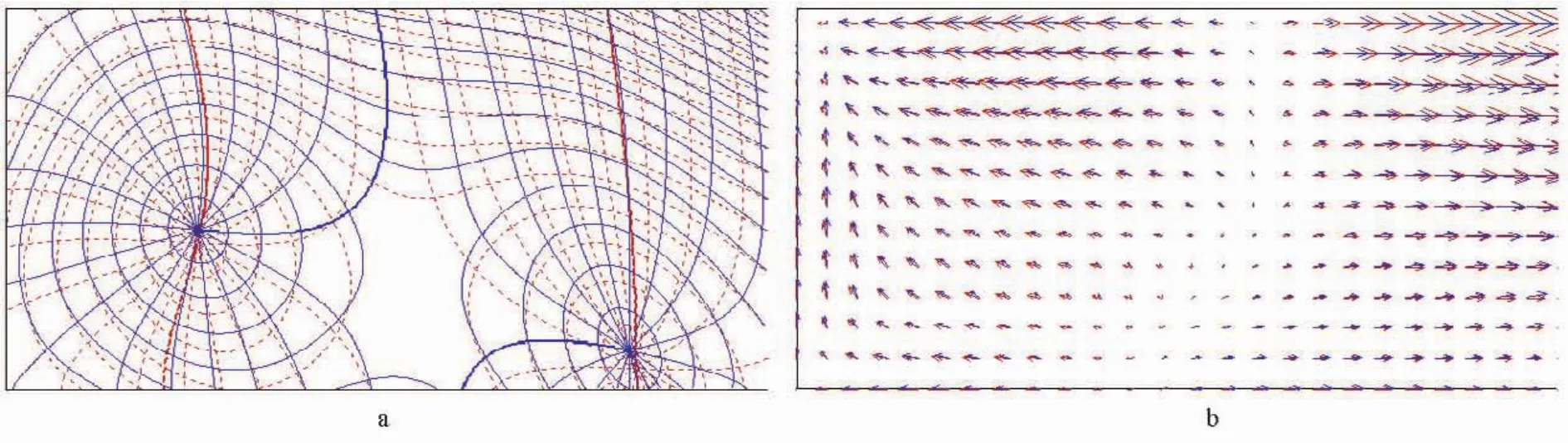
图2 等深矩形海湾模型验证图Fig.2 Model validation in the semi-enclosed rectangular basin of uniform water depth

4 驻潮波的形成及其位置

4.1 丁坝条件下等深矩形海湾潮波和潮流特性

将山东半岛岸形概化为巨型丁坝后置于半封闭等深矩形海湾中，参数设定与之前相同，半封闭等深矩形海湾在有无丁坝情形下的同潮图对比如图3。其中，红线代表半封闭等深矩形海湾同潮图结果，蓝线代表丁坝条件下等深矩形海湾同潮图结果。

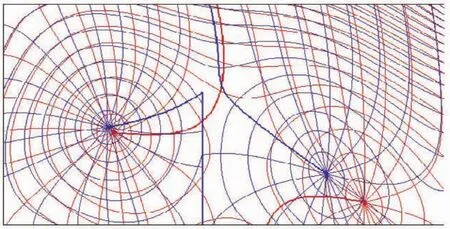
图3 有无丁坝条件下矩形海湾同潮图对比Fig.3 Comparison of co-tidal maps in the semi-enclosed rectangular basin of uniform water depth with and without coastal barrier

由图3可见，无巨型丁坝时，内无潮点（指靠近湾顶的无潮点）距离湾顶约252 km，大致位于1／4的潮波波长（距离湾顶290 km）附近，而外无潮点（指靠近湾口的无潮点）距离湾顶约820 km，大致位于3／4的潮波波长（距离湾顶870 km）附近；当巨型丁坝存在时，内无潮点依旧大约处于1／4潮波波长附近，但外无潮点距离湾顶736 km，大致位于1／2潮波波长（距离湾顶580 km）与3／4潮波波长（距离湾顶870 km）之间，而外无潮点距离巨型丁坝约278 km，大致位于1／4潮波波长（距离巨型丁坝290 km）附近。可见，原来的外无潮点是由于湾顶反射潮波传播到口外与前进潮波相互作用形成的第二个无潮点，而巨型丁坝存在条件下的外无潮点则是由于巨型丁坝引起的反射潮波与前进潮波相互作用形成的第一个无潮点。

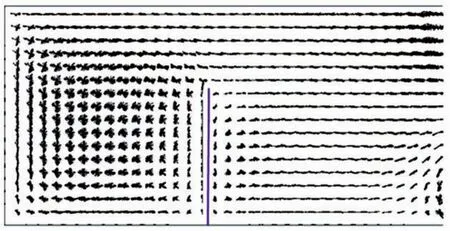
图4 丁坝条件下等深矩形海湾潮流椭圆图Fig.4 Tidal current ellipses in the semi-enclosed rectangular basin of uniform water depth with coastal barrier

半封闭等深矩形海湾在丁坝条件下的潮流椭圆图如图4所示。由图4可见，整个海湾内没有辐射状潮流场的出现，说明巨型丁坝的存在并不是辐射状潮流场形成的根本原因。

4.2 V型地形条件下无丁坝存在时矩形海湾潮波和潮流特性

黄海海底地势由北和东西两侧向中央和东南向倾斜，中央偏东有狭长低槽，自济州岛伸向渤海海峡，称为“黄海海槽”，槽的东侧坡陡，西侧平缓［29－30］。据此，将矩形海湾断面概化为图5a所示的不对称V型地形，其中左海岸（假设人面向湾顶，左手边为左海岸，右手边为右海岸）坡度为1∶5 848，右海岸坡度为1∶1 462，海槽处水深为68.4 m；为了对比不同海底地形对潮波和潮流特性的影响，在左海岸设计了另外两种不同的坡度，分别为1∶3 500和1∶1 462，如图5b、5c所示。

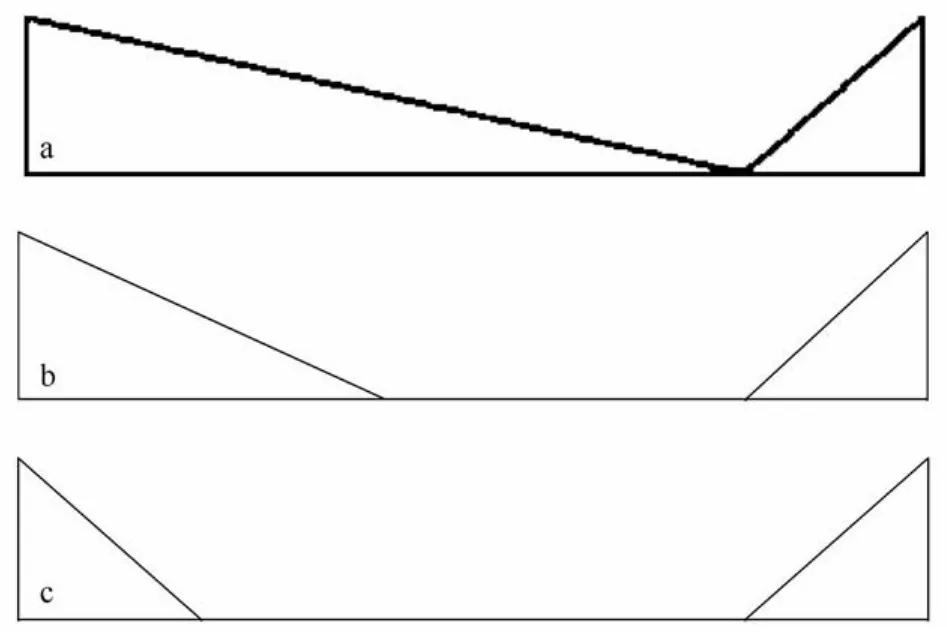
图5 V型地形概化图Fig.5 V-shaped topographies schematized for the Huanghai Sea

对不同地形下的半封闭矩形海湾进行数值试验，参数设定与之前相同。在无丁坝存在时，半封闭矩形海湾在上述3种不对称V型地形条件下的同潮图对比如图6。其中红线、绿线、黑线和蓝线依次分别代表半封闭矩形海湾等深地形、地形a、地形b和地形c条件下的同潮图结果。

图6 不同地形条件下矩形海湾同潮图对比Fig.6 Comparison of co-tidal maps in the basins with various submarine topographies

由图6可见，不对称V型地形对海湾内潮波分布的总体格局影响很大。内无潮点是由湾顶反射潮波与前进潮波相互作用在四分之一潮波波长附近形成的第一个无潮点，按c、b、a地形依次变化，由于平均水深依次变浅，潮波波长则变小，故位于距离湾顶约1／4潮波波长附近的内无潮点逐渐向湾顶方向靠近；内无潮点形成后，反射潮波继续向前传播，但由于传播距离进一步增大，反射潮能急剧耗散，以致在地形a条件下出现第二个无潮点蜕化的现象，在地形b和c条件下，尽管传播距离增大，但地形坡度的增大使平均水深增加，单位距离的潮能耗散相对减小，故总潮能耗散将小于地形a条件下，外无潮点将再次出现；此外，由于地形b的坡度小于地形c，使地形b下的潮能耗散将会大于地形c下，故地形b下的无潮点比地形c更靠近左岸，由于地形b的平均水深小于地形c，故地形b下的潮波波长将会小于地形c下，表现为地形b下的无潮点比地形c下更靠近湾顶。

由图6还可以看出，等深矩形海湾下的外无潮点比地形b、c下更靠近湾口，但地形b下的外无潮点比等深矩形海湾下更靠近左岸些，而地形c下的外无潮点则要比等深矩形海湾下更远离左岸。这一现象可做如下解释：由于等深矩形海湾下的平均水深大于地形b、c下，则等深矩形海湾下的潮波波长要大于地形b、c下，故大致位于3／4潮波波长附近的外无潮点在等深矩形海湾下必然要比地形b、c下更靠近湾口方向。潮能耗散的大小则取决于两个方面，一是受平均水深和底摩擦影响的单位距离潮能耗散，二是受平均水深和潮型控制的潮波传播距离。由于地形b下的平均水深较等深矩形海湾下明显为小，则其单位距离潮能耗散相对等深矩形海湾下显著为大，尽管对其而言潮波传播至外无潮点位置的距离较等深矩形海湾下为小，但总的潮能耗散却比它大，故地形b下的外无潮点比等深矩形海湾下更靠近左岸。由于地形c条件下的平均水深较等深矩形海湾下为小，则其单位距离潮能耗散相对等深矩形海湾下为大，但对其而言潮波传播至外无潮点位置的距离较等深矩形海湾下明显为小，以致其潮能耗散较等深矩形海湾下为小，故地形c条件下的外无潮点比等深矩形海湾下更远离左岸。

事实上，无潮点形成于入射潮波和反射潮波位相相反而振幅相等的位置。由于柯氏力的作用，入射潮波右岸振幅大而反射潮波左岸振幅大，无摩擦时振幅相等的点在海湾的中轴线上，此时无潮点就在湾中轴线上［15］；考虑摩擦条件下，反射潮波弱于入射潮波，振幅相等的位置必然偏向湾中轴线的左侧，底摩擦效应越大，反射潮波潮能耗散越大，这种偏移则越强烈，反之，底摩擦效应越小，反射潮波潮能耗散减弱，则无潮点将会向湾中轴线偏移。

图7 地形a条件下的潮流椭圆图Fig.7 Tidal current ellipes in the basin with the topography shown in Fig.5a

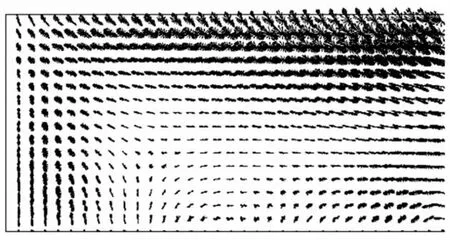
图8 地形b条件下的潮流椭圆图Fig.8 Tidal current ellipes in the basin with the topography shown in Fig.5b

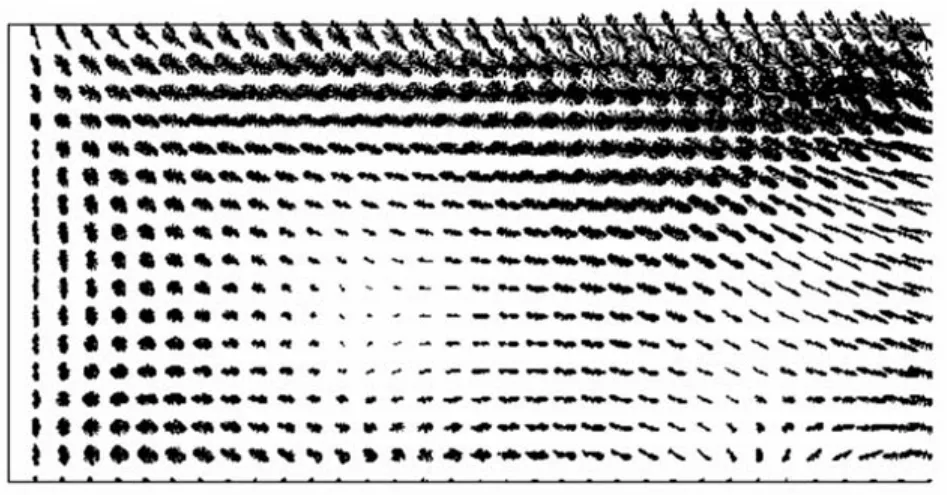
图9 地形c条件下的潮流椭圆图Fig.9 Tidal current ellipes in the basin with the topography shown in Fig.5c

图7～9为不同地形条件下海湾内潮流椭圆图。图7中靠近湾顶左岸附近的潮流椭圆主轴呈现明显的辐射状特征，而往湾口方向左岸区域内潮流椭圆主轴都偏转指向左岸；图8中靠近湾顶左岸附近的潮流椭圆主轴同样呈现显著的辐射状特征，左岸区域往湾口方向一端距离后潮流椭圆主轴又呈现辐射状分布，但此处不是很明显，进一步往湾口方向左岸区域的潮流椭圆主轴也都偏转指向左岸；图9中靠近湾顶左岸附近的潮流椭圆主轴呈现很不明显的辐射状特征，但左岸区域往湾口方向一端距离后出现一处很明显的呈辐射状特征的潮流椭圆主轴分布。事实上，整个海湾内共有两个波腹区，即内波腹区（指靠近湾顶的波腹区）和外波腹区（指靠近湾口的波腹区），在倾斜海底地形a、b、c下，分别在左岸形成内辐射状潮流场和外辐射状潮流场。在海底地形a和b下，由于平均水深相对较小，反射潮波在传播至湾口附近过程中急剧衰减，故在外波腹区辐射状潮流场左翼特征不突出。以上结果是在倾斜海底地形条件下才得以呈现，可见倾斜海底地形对辐射状潮流场的形成具有深刻的影响。

4.3 组合条件下矩形海湾潮波和潮流特性

在综合考虑巨型丁坝和不对称V型地形a的组合条件下对半封闭矩形海湾内的潮波和潮流进行数值试验，参数设定与之前相同，带丁坝型矩形海湾在地形a条件下与等深条件下同潮图对比如图10所示，其中蓝线代表带丁坝型的半封闭等深矩形海湾同潮图结果，而橙线则代表带丁坝型的地形a条件下的半封闭矩形海湾同潮图结果。

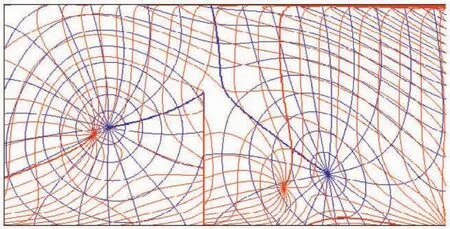
图10 带丁坝型矩形海湾等深条件下与地形a条件下同潮图对比Fig.10 Comparison of co-tidal maps in the semi-enclosed rectangular basins with coastal barrier，one is with uniform water depth and the other is with the topography shown in Fig.5a

由上图10可见，带丁坝型矩形海湾在地形a条件下的外无潮点相对巨型丁坝的距离较等深条件下为小，这是因为地形a使平均水深变浅后潮波波长变小的缘故。此外，该外无潮点相对左岸距离也较等深条件下为小，这是因为地形a使平均水深变浅后潮能耗散增大的缘故。

图11所示为带丁坝型矩形海湾在地形a条件下的潮流椭圆图。从图中可以看出，巨型丁坝前方（海湾外侧）存在一个较为明显的呈辐射状特征的潮流椭圆主轴分布。与无丁坝情形不同的是，该辐射状特征的潮流椭圆主轴分布是由于巨型丁坝引起的反射潮波与前进潮波相互作用形成的第一个波腹区在左岸倾斜海底地形的作用下所形成的。由此看出，在考虑柯氏力影响和潮波反射作用后，无论巨型丁坝是否存在，只要存在适当条件的倾斜海底地形，均能在矩形海湾的左岸外侧形成辐射状潮流场，但两者形成的机制不尽相同。

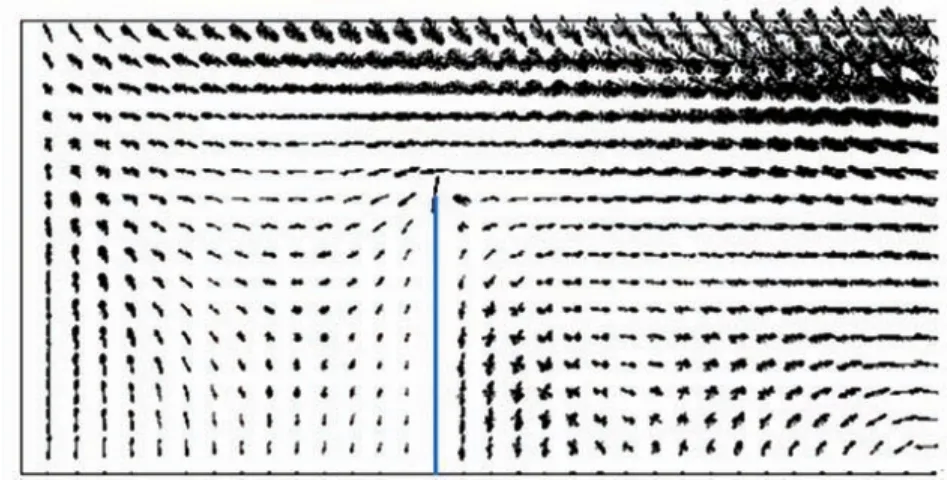
图11 组合条件下的潮流椭圆图Fig.11 Tidal current ellipes in the basin with the topography shown in Fig.5a

4.4 地形对无潮点和辐射状潮流场顶端位置的影响

以地形a条件下的带丁坝型半封闭矩形海湾为基础，将巨型丁坝往湾口方向的海底地形概化为如图5所示的3种不同地形，地形坡度均与前文保持一致。将带丁坝型的半封闭矩形海湾与上述3种不同海底地形分别进行组合，对各组合条件下矩形海湾内潮波和潮流进行数值试验，参数设定与之前相同，带丁坝型的半封闭矩形海湾在上述3种不对称V型地形条件下的同潮图对比如图12，其中红线、绿线、蓝线依次分别代表带丁坝型的半封闭矩形海湾在地形a、地形b和地形c条件下的同潮图结果。

图12 不同地形条件下带丁坝型矩形海湾同潮图对比Fig.12 Comparison of co-tidal maps in the basins with the topographies shown in Fig.5a，Fig.5b and Fig.5c

由图12可见，矩形海湾内潮波系统的总体格局没有发生改变，内、外无潮点依旧存在，但随着倾斜海底地形坡度的变陡，外无潮点呈现向湾中轴线和湾口方向偏移的现象。这样的结果是可以理解的：由于海底地形岸坡变陡，平均水深则加大，使潮波波长增加，故外无潮点有往湾口方向偏移的趋势；同样，由于平均水深的加大，底摩擦效应则减弱，故外无潮点有向湾中轴线方向靠拢的趋势。

同时，由上图12还可见，不同地形条件下，海湾潮波的同潮时线在左岸外辐射状潮流场位置附近呈现以辐射状潮流场顶端位置为顶点的弧形分布。随着地形坡度的增加，弧形状的同潮时线逐渐朝湾口方向发生明显偏移，这意味着辐射状潮流场顶端位置也朝湾口方向发生偏移，这是由于平均水深的加大致使潮波波长增大，从而引起波腹区向湾口方向偏移。

5 结论

本文将黄渤海海域概化为矩形海湾，海底概化为V型地形，山东半岛概化为垂直于海岸的巨型丁坝，基于DELFT3D-FLOW计算模块建立了适应于带丁坝型半封闭矩形海湾的平面二维数学模型。通过讨论半封闭矩形海湾中无潮点和辐射状潮流场的形成机制和偏移机理等问题，得出以下结论：

（1）考虑科氏力的存在和湾顶或巨型丁坝的反射作用，无潮点大致形成于1／4或3／4潮波波长附近，对于确定的潮型和海底摩擦，潮能耗散越大，无潮点越靠近左岸。而潮波波长和潮能耗散又取决于水深情况，故无潮点的位置最终取决于水深分布，且随着平均水深的增大，无潮点将向湾口和湾中轴线方向偏移。

（2）无论巨型丁坝是否存在，在等水深条件下海湾内没有形成辐射状潮流场，而叠加上倾斜海底地形后其得以形成，这表明倾斜海底地形对辐射状潮流场的形成具有深刻影响。所形成的辐射状潮流场大致位于波腹区的靠岸侧，且其顶端位置受水深影响明显，随着平均水深的增大，辐射状潮流场顶部呈现向湾口方向偏移的规律。

（3）有无巨型丁坝时所形成的外无潮点和外辐射状潮流场有着本质的区别：无巨型丁坝时，外无潮点是由湾顶反射潮波与前进潮波相互作用形成的第二个无潮点，外辐射状潮流场是由湾顶反射潮波与前进潮波相互作用形成的第二个波腹区在倾斜海底地形作用下形成的第二个辐射状潮流场；而巨型丁坝存在条件下，外无潮点是由巨型丁坝引起的反射潮波与前进潮波相互作用形成的第一个无潮点，外辐射状潮流场是由巨型丁坝引起的反射潮波与前进潮波相互作用形成的第一个波腹区在倾斜海底地形作用下形成的第一个辐射状潮流场。

本文所采用的概化模型具有一定的优势，它能够通过简单的模型将研究对象的多个复杂影响因素分别进行独立分析，并能够阐明研究现象的基本原理，但它只能定性说明这些现象，为了更为精细地反映实际情况，在后续研究中拟将对实际海域开展相关的数学模型研究。

［1］Ogura S.The tides in the northern part of the Hwang Hai［J］.Japanese Journal of Astronomy and Geophysics，1936，14（1）：27－55.

［2］Fang G H.Tide and tidal current charts for the marginal seas adjacent to China［J］.Chinese Journal of Oceanology and Limnology，1986，4（1）：1－16.

［3］沈育疆.东中国海潮汐数值计算［J］.山东海洋学院学报，1980，10（3）：26－35.

［4］夏综万，王钟桾.黄海M2分潮的数值模拟［J］.黄渤海海洋，1984，2（1）：1－7.

［5］赵保仁，方国洪，曹德明.渤、黄、东海潮汐潮流的数值模拟［J］.海洋学报，1994，16（5）：1－10.

［6］叶安乐，梅丽明.渤黄东海潮波数值模拟［J］.海洋与湖沼，1995，26（1）：63－70.

［7］沈育疆，叶安乐.东中国海三维半日潮流场数值计算［J］.海洋湖沼通报，1984（1）：1－10.

［8］万振文，乔方利，袁业立.渤、黄、东海三维潮波运动数值模拟［J］.海洋与湖沼，1998，29（6）：611－616.

［9］王凯，方国洪，冯士筰.渤海、黄海、东海M2潮汐潮流的三维数值模拟［J］.海洋学报，1999，21（4）：1－13.

［10］李培良，左军成，吴德星，等.渤、黄、东海同化TOPEX／POSEIDON高度计资料的半日分潮数值模拟［J］.海洋与湖沼，2005，36（1）：24－30.

［11］Zhang C K，Zhang D S，Zhang J L，et al.Tidal current-induced formation-storm-induced change-tidal current-induced recovery-Interpretation of depositional dynamics of formation and evolution of radial sand ridges on the Yellow Sea seafloor［J］.Science in China（Series D），1999，42（1）：1－12.

［12］An H S.A numerical experiment of the M2tide in the Yellow Sea［J］.Journal of the Oceanographical Society of Japan，1977，33：103－110.

［13］黄易畅，汤毓祥.江苏沿岸的潮汐运动：Ⅰ.潮汐运动的特征［J］.黄渤海海洋，1988，6（2）：6－11.

［14］张东生，张君伦.黄海海底辐射沙洲区的M2潮波［J］.河海大学学报，1996，24（5）：35－40.

［15］Taylor G I.Tidal oscillation in gulfs and rectangular basins［J］.Proceeding of the London Mathematical Society，1921，20（2）：148－181.

［16］Davies A M，Jones J E.The influence of bottom and internal friction upon tidal currents：Taylor's problem in three dimensions［J］.Continental Shelf Research，1995，15（10）：1251－1285.

［17］Rizal S.Taylor's problem-influences on the spatial distribution of real and virtual amphidromes［J］.Continental Shelf Research，2002，22（15）：2147－2158.

［18］Kagan B A，Romanenkov D A.Effect of hydrodynamic properties of the sea bottom on the tidal dynamics in a rectangular basin［J］.Atmospheric and Oceanic Physics，2006，42（6）：777－784.

［19］叶安乐，陈宗镛.半封闭矩形海域中海底地形对旋转潮波系统的影响［J］.山东海洋学院学报，1987，17（2）：1－7.

［20］Stocker T.A numerical Study of topographic wave reflection in semi-infinite channels［J］.Journal of Physical Oceanography，1988，18：609－618.

［21］de Boer W P，Roos P C.An idealized model of tidal dynamics in semi-enclosed basins：The effects of a mega-scale sand extraction trench in the North Sea［J］.Coastal Engineering，2010，58（8）：678－689.

［22］Roos P C，Velema JJ，Hulscher SJ，et al.An idealized model of tidal dynamics in the North Sea：resonance properties and response to large-scale changes［J］.Ocean Dynamics，2011，61（12）：2019－2035.

［23］Roos P C，Schuttelaars H M.Influence of topography on tide propagation and amplification in semi-enclosed basins［J］.Ocean Dynamics，2011，61（1）：21－38.

［24］Kang Yong Q.An analytic model of tidal waves in the Yellow Sea［J］.Journal of Marine Research，1984，42（3）：473－485.

［25］Kang S K，Chung J Y，Kang Y Q，et al.An analytical model of co-oscillating tide under frictional effect in the Yellow Sea［J］.Journal of Korean Society of Oceanography，1999，34（1）：22－35.

［26］沈育疆，黄岱岩，钱成春.试释黄海半日潮波系统形成机制［J］.海洋学报，1993，15（6）：16－24.

［27］Fang Z，Ye A，Fang G.Solutions of tidal motions in a semi-closed rectangular gulf with open boundary condition specified［J］.Tidal Hydrodynamics，1991：153－168.

［28］方国洪，王仁树.海湾的潮汐与潮流［J］.海洋与湖沼，1966，8（1）：60－77.

［29］林美华，毛彦平.南黄海海底地势分区［J］.海洋科学，1989（4）：21－24.

［30］林美华.黄海海底地貌分区及地貌类型［J］.海洋科学，1989（6）：7－15.

Tidal wave and tidal current characteristics of the M2constituent in a semi-enclosed rectangular basin with a coastal barrier

Qian Xuesheng1，2，Chen Yongping1，2，Zhang Changkuan2

（1.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering，Hohai University，Nanjing 210098，China；2.College of Harbor，Coastal and Offshore Engineering，Hohai University，Nanjing 210098，China）

A model of a semi-enclosed rectangular basin with a coastal barrier is schematized from the Bohai Sea，the Huanghai Sea and Shandong Peninsula.Using the DELFT3D-FLOW numerical model，we have conducted the analyses of the tidal characteristics of the M2constituent，the formation mechanism of the amphidromic points and the radial tidal current field in the basin.The results show that，due to the Coriolis force and the barrier reflection，there will always present an amphidromic point in front of the coastal barrier.However，the radial tidal field is absent in the case of uniform water depth with an exception of the existence of mild slope in the nearshore topography.It is found that the locations of the focal point of the radial tidal current field and the amphidromic point are affected by the mean water depth.With the increase of the mean water depth，the location of the amphidromic point will shift to the entrance and the central axis of the basin，while the focal point of the radial tidal current field will move towards the entrance of the basin.The findings in the paper will facilitate the understanding of the formation mechanism and dynamic characteristics of stationary tidal wave in this type of the basin.

rectangular basin with a coastal barrier；M2tidal constituent；stationary tidal wave；amphidromic point；radial tidal current field

P731.23

A

0253-4193（2014）09-0037-08

钱学生，陈永平，张长宽.带丁坝型半封闭矩形海湾中M2分潮潮波和潮流特性分析［J］.海洋学报，2014，36（9）：37—44，

10.3969／j.issn.0253-4193.2014.09.005

Qian Xuesheng，Chen Yongping，Zhang Changkuan.Tide wave and tidal current characteristics of the M2constituent in a semi-enclosed rectangular basin with a coastal barrier［J］.Acta Oceanologica Sinica（in Chinese），2014，36（9）：37—44，doi：10.3969／j.issn.0253-4193.2014.09.005

2013-08-01；

2013-11-25。

国家自然科学基金面上项目（51179067，51379072）；水利部公益性行业科研专项经费项目（201201045）；江苏省普通高校研究生科研创新计划项目（CXZZ12_0254）。

钱学生（1989—），男，江苏省泰州市人，主要从事近海水动力数值模拟和海洋新能源等方面的研究。E-mail：clarkqianxuesheng＠163.com

*通信作者：陈永平，教授，主要从事环境水力学、海岸动力学的试验和数值模拟研究。E-mail：yongping_chen＠hotmail.com