波浪破碎下油滴粒径分布理论模型研究

孙宝楠，袁业立，韩磊，杨永增*，连展

（1.中国海洋大学海洋环境学院，山东青岛 266100；2.国家海洋局第一海洋研究所，山东青岛 266061；3.海洋环境科学和数值模拟国家海洋局重点实验室，山东青岛 266061）

波浪破碎下油滴粒径分布理论模型研究

孙宝楠1，2，3，袁业立2，3，韩磊2，3，杨永增2，3*，连展2，3

（1.中国海洋大学海洋环境学院，山东青岛 266100；2.国家海洋局第一海洋研究所，山东青岛 266061；3.海洋环境科学和数值模拟国家海洋局重点实验室，山东青岛 266061）

海上溢油在波浪破碎的情况下经常会形成油滴，本文讨论了油滴形成的可能机制，根据量纲分析瑞利法建立了油滴卷入率与能量耗散率、卷入深度等破碎统计物理量的关系。基于量纲分析Π定理并根据毛细数、无量纲卷入时间与粘度比的实验关系，导出了油径谱的理论模型。初步结果表明，理论谱斜率－2.29与观测谱斜率－2.3符合良好，剪切率、表面张力、油滴半径、油和水的黏度等因素是影响油滴总数的主要原因。

量纲分析法；卷入率；油径谱；波浪破碎统计量

1 引言

近年来，海上溢油是造成海洋环境污染的主要因素之一。海上溢油在海风、海浪和海流的综合作用下进行扩展、漂移、蒸发、乳化、溶解、分散、沉降、岸上吸附、光解和生物沉降等过程。一部分溢油覆盖在水面，另一部分则以油滴的形式大量分散在水中［1］。海洋动力过程对油膜的影响主要体现在油膜的漂移和分散方面，而以往的研究大部分只关注溢油的漂移路径，对于溢油分散过程即破碎波作用下的溢油入水、油滴生成方面的研究还比较少［2］。观测表明，高海况下被破碎波卷入水下的溢油量可以达到溢油总量的50%以上，波浪破碎是溢油以油滴形式入水的主要机制［3］，与实际海浪破碎相联系的油滴生成问题及其分布规律是溢油分散领域尚未研究透彻的课题。

破碎波作用下油滴的分布是溢油分散过程的基本问题，其具有很强的规律性。前人观测的谱斜率结果在－2.3左右［4］。迄今对油径谱的研究主要集中在实验结果的简单拟合，不能反映油径分布规律的内在联系，也不能反映实际海况对油滴分布的影响，所以亟须提出一种结合油滴形成机制和实际海洋参量的理论模型。本文探讨了油滴形成的可能机制，引入了Yuan等［5］破碎波统计物理模型，讨论了毛细数、无量纲卷入时间与油水黏度比的关系，并应用量纲分析法建立了破碎波影响下的油滴粒径分布理论模型，理论结果揭示了控制油滴总数的影响因素并从理论解释了油径分布规律的实验结果。

2 理论与观测研究成果

2.1 油径谱的理论研究

早在20世纪30年代，油滴的生成、破碎和分布规律就已经引起了科学家们的注意。Taylor［6］的研究认为，牛顿型液-液两相乳化液的分散相液滴在外力场的作用下会同时发生拉伸、破裂和聚合现象。小液滴发生碰撞聚合，大液滴被剪切，最终达到分散液滴的动态平衡，毛细数和黏度比是影响液滴变形的主要因素。对于海上溢油来说，油滴总数随其半径变化的分布便是油径谱。油径谱达到稳定后存在能够经受外力而不会发生破裂的最大油滴半径，Hinze［7］采用量纲分析法根据韦伯数临界值和Kolmogorov湍流惯性子区理论得到油滴最大直径的理论表达。Li和Garrett［2］假设油滴在破碎过程中受两种不同的机制控制，湍流耗散率较小时，湍流动压占主导；湍流耗散率较大时，黏性剪切代替湍流动压起主导作用。近20年来，引入海洋环境要素研究溢油入水过程逐渐成为研究的焦点，Johansen［8］将风应力作为油滴垂向卷入的主要因素，并引入白冠覆盖率作为衡量溢油卷入率的尺度。Mackay等［9］提出油滴分散参数化模型，认为风速、黏度、油水界面张力和油膜厚度对入水量具有很大影响。Riemsdijk将溢油入水量与波浪要素联系起来，建立了简单的溢油入水量模型［10］。Tsouris和Tavlarides［11］提出模拟油滴数量的简单动力模型。挪威的IKU模型、英国的OSIS模型、美国的ADIOS模型均采用Delvigne的实验室模型计算油滴的分散量［12］。但以上研究中未对实际海洋破碎动力过程在溢油分散中的影响进行定量的讨论，也未深入分析油滴控制机制间的内在联系。所以，要弄清楚这些问题必须把破碎波统计要素和油滴生成控制机制结合起来，才能提出更加符合实际的理论模型。研究该理论模型可为油滴动力平衡谱作参考，也可快速估计破碎波影响下的溢油入水量。

2.2 油径谱的观测研究

由于海上观测破碎波携油入水的过程较困难，相关研究主要集中在实验室中，Forrester［13］、Delvigne［14—16］、Bouwmeester和Wallace［17］的研究得到了不少沿用至今的结论。其中，代尔夫特水动力实验室的Delvigne和他的同事们的研究最为突出（后简称D＆S实验）。D＆S实验对破碎波作用下的溢油卷入深度、油滴粒径分布规律等做了详细的实验研究。实验中使用激光束粒子筛选器计算水中油粒子的数目，采用高频紫外光束将油滴、气泡和灰尘粒子区分开来，最小可探测出3μm的微观粒子。实验结果表明，油滴的最大尺寸依赖于油的黏度和平均能量耗散率等因素，一般不大于2 000μm，平均尺寸在200μm左右，油膜垂直扩散率介于每小时0.4%～2.1%。在不同油品、不同破碎能量、不同油膜厚度的试验中总能得到油滴粒径较统一的分布律［14］。如图1所示，油滴数量N（纵坐标）与油滴粒径a（横坐标）呈对数线性关系：N～a－2.3。Bouwmeester和Wallace［17］设计的溢油水槽实验表明，在表层水体附近油滴分布遵循分布律N～a－1。油滴卷入实验均表明，油滴数量分布显著依赖于油滴粒径尺度，两者的对数呈明显线性关系，但对于存在这种关系的内部原因，目前的研究还并不充分。本文在第三部分中，将应用量纲分析法，结合破碎波统计量从理论上解释油径分布规律的可能原因。

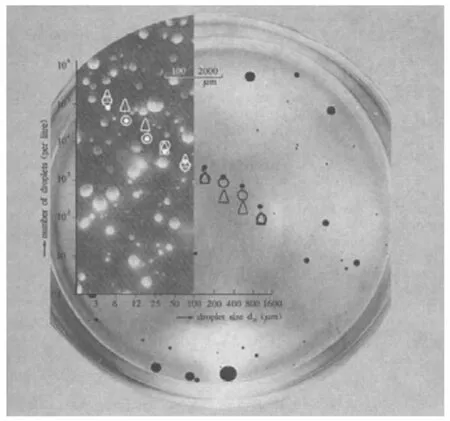
图1 破碎波携油入水得到的油滴样本及粒径分布规律（据文献［16］修改）Fig.1 Dispersion sample of oil droplet under breaking waves and observed droplet size distribution（modified from literature［16］）

3 油径谱理论模型的建立

3.1 量纲分析法

量纲分析法主要用于分析物理现象中的内部规律，通过对有关物理量做量纲幂次分析，将它们组合成无量纲的组合量，揭示物理量之间在量纲上的内在联系，特别是对那些很难从理论上进行分析的复杂问题，更能显示出该方法的优越性。Maxwell提出长度（L）、质量（M）、时间（T）的计量单位为“基础单位”，其他单位为“衍生单位”，对力学问题来说，任一物理量的量纲均可表示为L-M-T的幂次之积。Rayleigh提出了用定性物理量的某种幂次之积的函数来表示被决定的物理量，对于变量较少的简单过程，瑞利法可以方便地直接求出结果。对于变量较多的复杂过程，此法有局限性。Buckingham建立的量纲分析Π定理，可以解决较多物理量的复杂问题。根据Π定理，如果一个物理过程涉及n个物理量和m个基本量纲，Π定理可给出将该方程等价地重写为具有n－m个无量纲参数方程（Π方程）的方法［18—20］。在油滴分布规律的研究中，采用量纲分析法并结合实验室观测可以得到各种控制因素之间的内部联系，可避免重要因素的重复或缺失。

3.2 溢油入水卷入率模型的建立

石油一旦溢漏到海上，将在破碎波的作用下以小油滴的形式进入水中。如果油滴足够小，湍流将阻止油滴上浮，此过程被称为分散。在恶劣海况下，溢油的分散是自然去除浮油的主要机理，在众多溢油事件中，大部分的浮油都以油滴的形式被分散到水中［21］。自然分散条件下，波浪破碎的能量较大或浮油的黏度很低时，这一过程是非常显著的，所以破碎波是引起溢油入水的最直接最主要的因素。在海况较平静时，溢油入水很小，油水界面张力也会导致溢油入水，但与波浪作用相比量级很小。实验表明，波浪破碎过程中大部分的能量都用来克服浮力做功。同样，我们可以假设波浪破碎的过程中，一定比例的能量用来克服浮力携油入水，Lamarre和Melville［22］认为这部分能量大约为破碎能量的0.3～0.5倍。根据Johanson［8］、Tkalich和Chan［23］的一阶模型，把从浮油到混合层的油滴质量用运动方程描述为：

式中，Ms是浮油的质量，Me是混合层里油的质量（均表示单位海表面积下的量值），Qo为单位质量的浮油被破碎波卷入的速率。由式（1）可以看出，卷入率Qo在卷入过程中起着决定性的作用。卷入率所涉及的变量不多，可利用瑞利法进行以下步骤的量纲分析［18—19］。

（1）根据理论和实验可知卷入率Qo与单位时间、单位水体上海波破碎损耗的能量Et／Vb、油滴密度ρ、油滴重力gz有关，其中z油滴卷入深度、g为重力加速度。

（2）将它们写成指数乘积关系Qo＝k（Et／Vb）aρb（ gz）c，其中，k是无量纲量，并且取基本量纲为长度量纲L、时间量纲T和质量量纲M。

（3）对基本物理量进行量纲分析并利用量纲和谐原理求出待定指数：

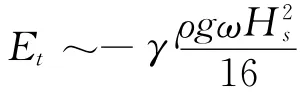
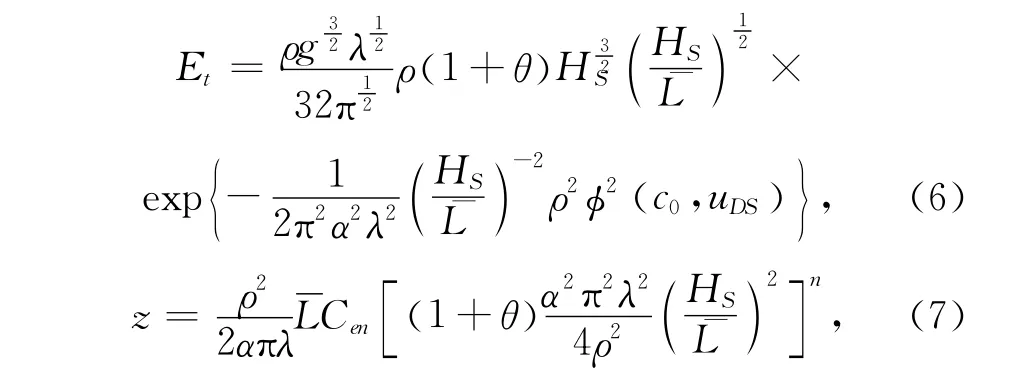
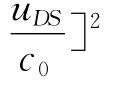
3.3 油径谱理论模型的建立

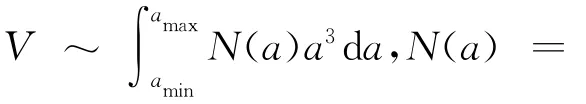
破碎波加强了湍流的剪切作用，使油滴发生形变导致破碎，在Hinze微长度尺度内，表面张力是抵制油滴破碎的原因，当表面张力不足以抵制剪切造成表面变形，油滴将发生破裂，这个过程主要由毛细数Ca即界面张力数控制［3］。毛细数为流体黏性力和界面张力的比值［7］，同时也是韦伯数We和雷诺数Re的比值，在流体力学中可预测两相流体分散相液滴的形变和破裂发生的可能性［28］。实验表明，毛细数、无量纲卷入时间与分散相和连续相的黏度比λ存在对数线性关系［2］（图2）。所以，假设油径谱是关于油滴半径a、油滴动力黏度μd、水的动力黏度μ、油滴所受的剪切率S、卷入率Qo、表面张力系数γ的函数。综上所述，运用量纲分析法的Π定理可以对以上相关物理量进行量纲分析（表1）。

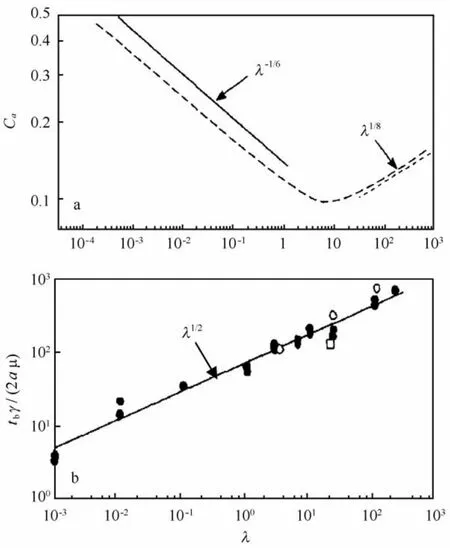
图2 毛细数（a）和无量纲时间（b）随黏度比的变化曲线（据文献［3］修改）Fig.2 Critical capillary number（a）and dimensionless time（b）as a function of viscosity ratio（modified from reference［3］）

表1 各物理量的量纲分析Tab.1 Dimensional analysis of various physical quantities

倘若此物理过程的方程式为F（a，μ，μd，S，N，Q0，γ）＝0，其中涉及M-L-T 3个基本量纲和7个物理量，则存在4个无量纲Π数，根据量纲和谐原理，具体为：

所以，只要求出n的值，就可导得油径谱的模型。

根据图3a可知，油滴半径与湍流耗散率的关系在不同的控制机制下表现为不同的斜率，而D＆S实验的半径大都落在－2／5次方率的区间上，所以a～ε－2／5。

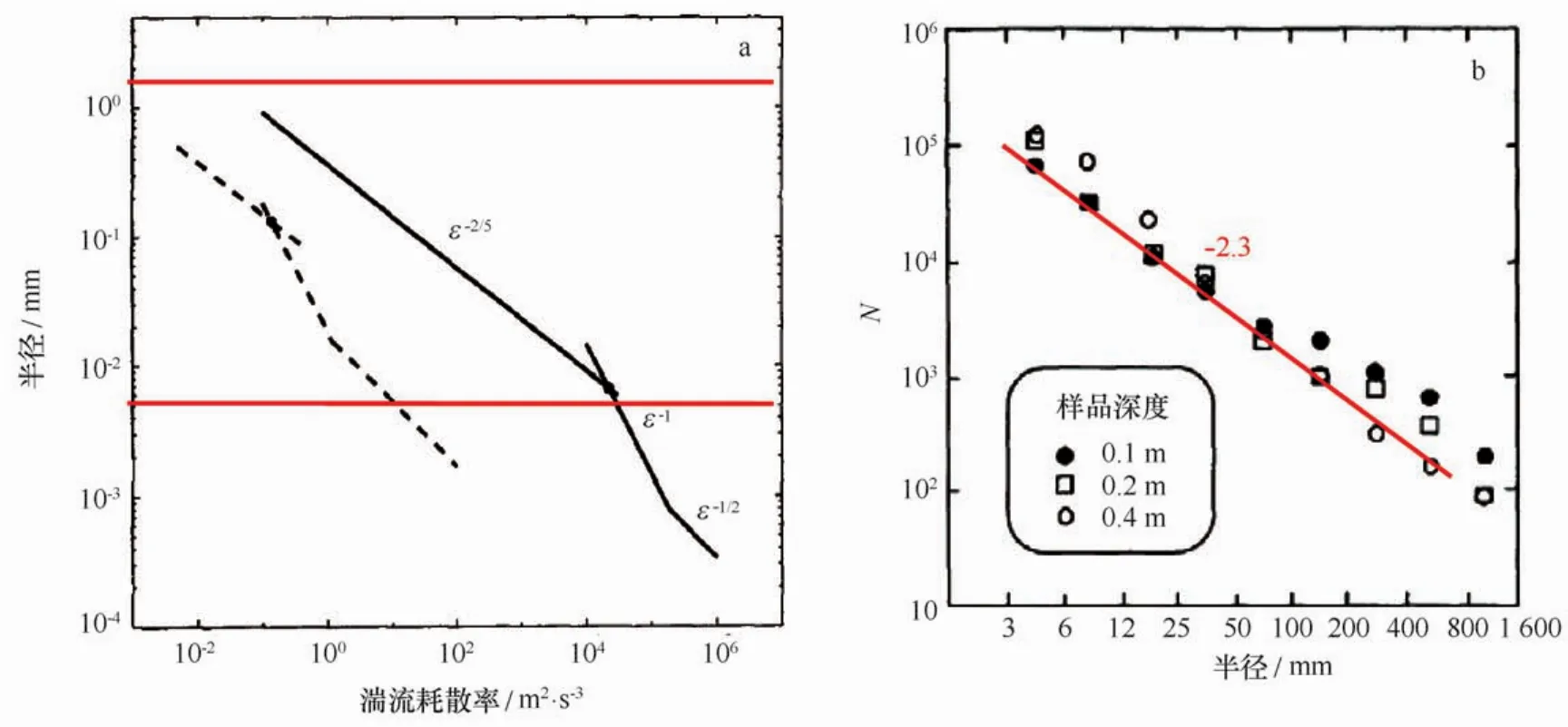
图3 Prudhoe湾样本油滴半径随湍流耗散率的变化曲线（a）和D＆S实验3种深度处的油滴粒径分布（b）（据文献［3］修改）Fig.3 Curves of Prudhoe Bay oil droplet radius changing with dissipation rate（a）and droplet size distribution versus droplet radius at three depths from D＆S experiments（b）（modified from reference［3］）

当油滴尺寸大于Kolmogorov长度尺度，剪切率S＝2.3ε1／3a－2／3［2］，根据式（10）、a和ε幂次率的关系可得到：

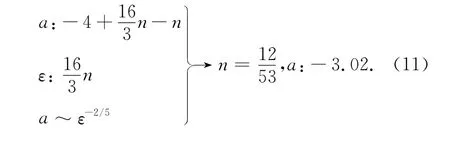
当油滴尺寸小于Kolmogorov长度尺度，剪切率S＝3.65ε1／2ν1／2［2］，根据式（10），a和ε的幂次率的关系可得到：

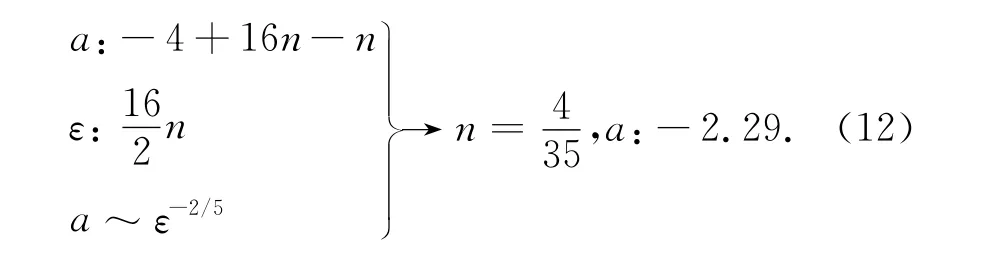
所以，需要确定试验中的Kolmogorov长度尺度，才能确定油径谱斜率。Kolmogorov长度尺度是指在湍流中黏性开始起作用的微长度尺度［6］。D＆S试验中Prudhoe湾油样运动黏度ν＝40～120 cst，能量耗散率ε＝0.1～1 m2s－3［4］。根据Kolmogorov长度尺度的定义式η＝ （ν3／ε）1／4，η最小为0.08 m，观测油滴尺度在3～1 200μm远小于这个值，所以黏性起到主要的控制作用。油径斜率选择式（12）的表达，即谱斜率式（13）变为：

式（13）即本文推导的油径谱理论模型，因为运动黏度ν和动力黏度μ的转换，引入了油滴密度ρd。为了考虑实际海浪破碎的影响，Q0可以选择式（5）至式（7）的表达。理论谱模型的谱斜率约为－2.29，这与D＆S实验观测的谱斜率－2.3非常接近，说明文中量纲分析所考虑的物理量和控制机制比较合理，较好的反应了观测谱的规律。从式（10）、（13）中可以看出，黏度、湍流耗散率、卷入率、表面张力系数等量均对油滴的总数有影响，黏度和湍流耗散率越大，油滴个数越多，油滴密度、表面张力系数越大，油滴个数越少。但卷入率对油滴总数影响不大，这可以理解为卷入率影响的是油滴卷入的时间，对油径谱的结构没有很大的贡献。

4 结论

本文应用量纲分析法，基于Yuan等［5］波浪破碎统计模型，导出油滴的卷入率理论形式，此模型可结合海浪数值模式定量估算波浪破碎过程带来的卷入效果。在此基础上，利用Π定理分析了油滴产生破碎过程的控制因素及4个无量纲相似数表达，在毛细数和无量纲卷入时间的观测基础上，建立了油滴总数与油滴半径、湍流能量耗散率、表面张力、黏度的关系，即油径谱的理论模型。

利用该油径谱模型初步解释了D＆S实验中油滴数量与油径的对数线性关系，而这一关系依赖于油和水的黏度、湍流耗散率、油滴表面张力、卷入率等物理量。初步结果表明，油径谱理论谱斜率为－2.29，与实验室观测的油径谱斜率－2.3非常接近，从理论上解释观测油径谱的规律和控制机制。基于量纲分析建立的油径谱模型还需要今后的观测实验进一步检验和完善。本文的理论研究和实际观测工作结合起来，可在海洋溢油的应急响应和评估中起到一定的参考作用。

致谢：感谢审稿人对本文提出的宝贵意见和建议。本研究得到科技部863项目、国家海洋局第一海洋研究所基本科研业务费专项资金项目的支持。

［1］赵文谦，江洧.石油以油滴的形式向水下扩散的研究［J］.环境科学学报，1990，10（2）：173－182.

［2］孙宝楠.波浪破碎过程对油滴垂直混合的作用研究［D］.青岛：国家海洋局第一海洋研究所，2010：1－50.

［3］Li M，Garrett C.The relationship between oil droplet size and upper ocean turbulence［J］.Marine Pollution Bulletin，1998，36：961－970.

［4］Delvigne G A L，Sweeney C E.Natural dispersion of oil［J］.Oil and Chemical Pollution，1988，4：281－310.

［5］Yuan Y L，Han L，Hua F，et al.The statistical theory of breaking entrainment depth and surface whitecap coverage of real sea waves［J］.Journal of Physical Oceanography，2009，39：143－161.

［6］Taylor G I.The viscosity of a fluid containing small drops of another fluid［J］.Proc R ScoLond，1932，A138：41－48.

［7］Hinze J.Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes［J］.AICHE Journal，1955，1：289－295.

［8］Johansen O.Dispersion of oil from drifting slicks［J］.Spill Technology Newsletter，1982（11／12）：134－149.

［9］Mackay D，Paterson S，Trudel K.A mathematical model of oil spill behavior［C］／／Report EE7，Environment Canada，Ottawa，1980.

［10］赵东至，张存智，徐恒振.海洋溢油灾害应急响应技术研究［M］.北京：海洋出版社，2006：186－191.

［11］Tsouris C，Tavlarides L L.Breakage and coalescence models for drops in turbulent dispersion［J］.AICHE J，1994，40（3）：395－406.

［12］蔡忠清.海上船舶溢油离子化及适应性数值模拟研究［D］.武汉：武汉理工大学，2010：1－30.

［13］Forrester W D.Distribution of suspended oil particles following the grounding of the tanker Arrow［J］.Journal of Marine Research，1971，29：151－170.

［14］Delvigne G A L，Sweeney C E.Natural dispersion of oil［J］.Oil and Chemical Pollution，1988，4：281－310.

［15］Delvigne G A L，Hulsen L J M.Simplified laboratory measurements of oil dispersion coefficient application in computations of natural oil dispersion［C］／／Proceedings of the 17th Arctic and Marine Oil Spill Program Technical Seminar.Environment Canada，1994：173－187.

［16］Delvigne G A L.On scale modeling of oil droplet formation from spilled oil［J］.Oil Spill Conference，1991：501－506.

［17］Bouwmeester R J B，Wallace R B.Oil entrainment by breaking waves［C］／／Proceedings of the Ninth Arctic Marine Oil Spill Program Technical Seminar.Environment Canada，1986：39－49.

［18］谈庆明.量纲分析［M］.合肥：中国科学技术大学出版社，2000：9－18.

［19］谢多夫.力学中的相似方法与量纲理论［M］.沈青，等译.北京：科学出版社，1982：1－151.

［20］林家翘.自然科学中确定性问题的应用数学［M］.北京：科学出版社，2012：210－238.

［21］Adios.Automated Data Inquiry for Oil Spills［M］／／User's Manual.NOAA／Hazardous Materials Response and Assessment Division，Seattle Washington，1994.

［22］Lamarre E，Melville W K.Air entrainment and dissipation in breaking waves［J］.Nature，1991，351：469－472.

［23］Tkalich P，Chan E S.A High Resolution Oil Spill Model［C］／／Proceedings of International Conference on Port and Maritime R＆D and Technology.Singapore，2001：647－652.

［24］Garrett C，Li M，Farmer D.The connection between bubble size spectra and energy dissipation rates in the upper ocean［J］.Phys Oceanography，2000，30：2163－2171.

［25］Deane G B，Stokes M D.Scale dependence of bubble creation mechanisms in breaking waves［J］.Nature，2002，418：839－844.

［26］张书文.波浪破碎气体的卷入过程及相关统计量的估计［J］.物理学报，2008，57（5）：3287－3292.

［27］Han L，Yuan Y L.Bubble size distribution in surface wave breaking entraining process［J］.Science in china，2007，50（11）：1754－1760.

［28］张洪武，周持兴.稳态双曲流场中液－液混合的粘性液滴哑铃分散模型［J］.高分子学报，1998，6：704－708.

On theoretical models for oil droplets size distribution under the influence of surface wave breaking

Sun Baonan1，2，3，Yuan Yeli2，3，Han Lei2，3，Yang Yongzeng2，3*，Lian Zhan2，3

（1.Laboratory of Physical Oceanography，Ocean University of China，Qingdao 266100，China；2.First Institute of Oceanography，State Oceanic Administration，Qingdao 266061，China；3.Key Lab of Marine Science and Numerical Modeling，State Oceanic Administration，Qingdao 266061，China）

Marine oil spill often forms oil droplets in stormy conditions..Based on the dimensional analysis Rayleigh method，the relationship is established between entrainment rate of oil droplet and statistical physical quantities such as the energy dissipation rate，intrusion depth et al.An expression of size spectrum of oil droplets is derived based onΠtheorem and relationship between capillary number，the dimensionless intrusion time and viscosity ratio.Preliminary results show that the slope of the derived spectrum is－2.29，which agrees well with the measured slope－2.3 in laboratory.Shear rate，surface tension，droplet radius，oil and water viscosity is the main factors controlling the total number of the oil droplets.

dimensional analysis；entrainment rate；size spectrum of oil droplets；surface wave breaking statistics

P731.22

A

0253-4193（2014）09-0030-07

孙宝楠，袁业立，韩磊，等.波浪破碎下油滴粒径分布理论模型研究［J］.海洋学报，2014，36（9）：30－36，

10.3969／j.issn.0253-4193.2014.09.004

Sun Baonan，Yuan Yeli，Han Lei，et al.On theoretical models for oil droplets size distribution under the influence of surface wave breaking［J］.Acta Oceanologica Sinica（in Chinese），2014，36（9）：30－36，doi：10.3969／j.issn.0253-4193.2014.09.004

2013-12-26；

2014-04-19。

国家高科技研究发展计划（863）（2013AA09A506）；国家海洋局第一海洋研究所基本科研业务费专项资金项目（GY0212148，GY0212181）。

孙宝楠（1984—），女，山东省青岛市人，研究实习员，主要从事海洋波动动力学研究。E-mail：sunbn＠fio.org.cn

*通信作者：杨永增（1969—），男，山东省泰安市人，研究员，主要从事海浪数值模拟研究。E-mail：yangyz＠fio.org.cn