基于WPSO的电力系统暂态稳定紧急控制

王义红，秦晓辉，周勤勇，王一兵

(1．中国电力科学研究院，北京100192;2．清华大学核能与新能源技术研究院，北京100084)

基于WPSO的电力系统暂态稳定紧急控制

王义红1，秦晓辉1，周勤勇1，王一兵2

(1．中国电力科学研究院，北京100192;2．清华大学核能与新能源技术研究院，北京100084)

在标准粒子群优化算法(SPSO)的基础上增加小波变异操作，形成一种新的混成粒子群优化算法(WPSO)。基于WPSO，针对特高压电网1000kV与500kV的暂态稳定紧急控制问题进行协调优化，该处暂态稳定包括了暂态电压稳定和暂态功角稳定，给出了不同特高压断面潮流对应的切机策略表，WPSO具有比SPSO更好的全局收敛特性并可以取得更高质量的最优解，在特高压电网试验示范工程进行的仿真验证了所提新方法的有效性。

粒子群优化算法;小波变异;暂态稳定;紧急控制

0 引言

电力系统三道防线的最重要内容之一是合理的安全稳定控制措施，而安全稳定控制措施中最常用的方法之一就是切机控制［1-6］。为了保证电力系统的暂态稳定性，电力系统内安装了大量的安全稳定控制装置，所有的控制策略均需离线制定并写入策略表以备紧急控制使用。实际工程一般采用试探法制定切机策略，该法通常得不到最优切机方案，尤其是针对特高压电网1000kV与500kV的协调控制，因其控制范围与控制量更大，控制规律也更复杂。

针对暂态稳定紧急控制，很多学者从不同角度给出了不同的研究方法，如半张量积法［7］、功率切换法［8］、混合法［9］、扩展等面积法［10］、最优控制原理法［11］、模糊风险分析法［12］、动态安全域法［13］、WAMS法［14］、快速时域仿真法［15］等等，本文将从全新的角度采用智能算法对其进行研究。

粒子群优化算法(PSO)是20世纪90年代提出的一种基于种群随机优化的算法。与其他随机优化算法相比，PSO足以比拟甚至拥有更先进的搜索性能，特别是针对一些比较难的优化问题，PSO具有更快的收敛速度以及更稳定的收敛效率［16］。近年来，PSO已经应用于电力系统很多领域，如电压稳定预防控制［17，18］、检修计划［19］、负荷预测［20］、ATC［21］及最优潮流［22］等。然而进一步的研究表明，粒子群算法在早期迭代时表现很好，但是常常在接近最优解的时候出现停滞现象［23，24］，将小波变异操作加入标准粒子群优化算法(SPSO)后形成的一种新的混成粒子群优化算法(WPSO)已经显示出了更好的全局收敛性［25］。

本文采用WPSO算法对特高压电网进行综合优化研究，提出风险性与经济性综合优化方法，以取得更可行和控制代价更小的协调控制措施。本文内容组织如下:第1节建立数学模型，包括目标函数与各类约束条件;第2节介绍粒子群优化算法及其算法实现;第3节针对特高压试验示范工程进行仿真分析;最后是结论。

1 数学模型

本文考虑的问题可以描述为:在发生不同严重故障的情况下，如何协调控制1000kV和500kV两侧以满足系统暂态功角稳定和暂态电压稳定的前提下，付出的代价最小。其模型可描述为

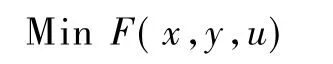
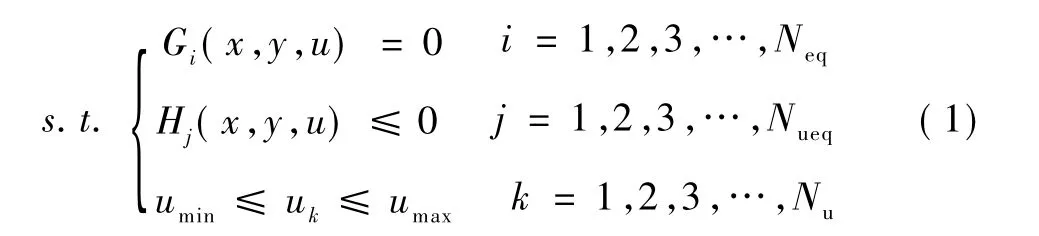
其中，F(x，y，u)是目标函数;Gi和Hi是等式和不等式约束;x是状态变量，如发电机及励磁系统的快动态变量、潮流变量等;y表示代数变量，如节点电压、相角等;u为控制变量，umax、umin分别是控制变量的上、下限;Neq、Nueq和 Nu分别为等式约束、不等式约束以及控制变量的总数。

下面逐一简单介绍目标函数与约束条件:

1.1 目标函数

优化问题(1)的目标函数选取各控制变量的改变量成本最低，即

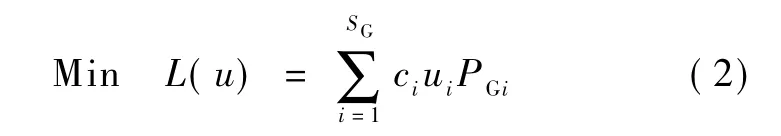
式中，L(u)是成本函数;i∈SG，SG表示可调有功发电机集合;ci是第 i台发电机的切机费用，方便起见，本文均设为1;ui是控制向量，本文中专指切机比例因子，由于工程上切机都采用整台切机方式，因此该比例因子非1即0;PGi是第i台发电机的初始出力。

1.2 等式约束

该优化问题的等式约束除了常规的系统潮流方程，还包括短期动态平衡方程，其表达式为

其中，x表示微分变量，如发电机励磁系统动态变量以及负荷动态变量;y表示代数变量，如节点电压、相角等。

1.3 暂态功角不等式约束

取系统的惯量中心COI作为参考，各发电机转子相对摇摆角极限为

式中，i∈SG，SG表示可调有功发电机集合;t∈St，St表示积分时段集合;δt(i)表示第i台发电机在第t时段的转子角;δmax、δmin分别是发电机转子相对摇摆角上、下限，本文中设置δmax为200°;δt(COI)=为发电机群在第t时段的惯性中心角度;Mj为第j台发电机的转动惯量。

1.4 暂态电压不等式约束

电力系统在受到扰动的过程中，负荷母线电压能够在10s以内恢复到0.8标称电压以上［1］。

实际应用时，可根据不同算例选择判定电压稳定的负荷母线监测点。

2 粒子群优化算法

2.1 标准粒子群优化算法(SPSO)

粒子群优化算法(PSO)［17，18］是一种新兴的最优化智能算法，方便起见，这里称之为标准粒子群优化算法(SPSO)。

令x和v分别代表一个粒子的坐标以及它相应的飞行速度。一个粒子先前最好的位置会被记录下来并表示为 pbest，所有粒子中最好的位置表示为gbest。每个粒子的速度和位置可以计算如下:

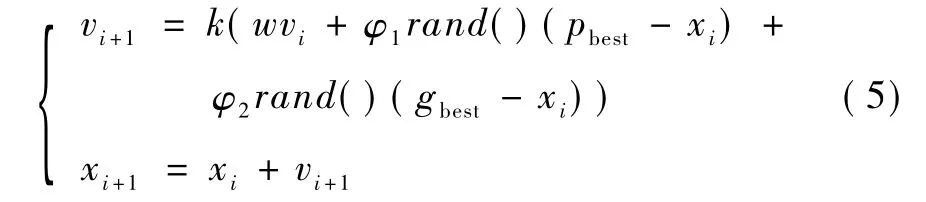
其中，xi和vi分别是第i代粒子的当前位置和速度; w是惯性加权因子;φ1和φ2是加速因子;rand()返回一个均匀分布在［0，1］之间的随机数;k是收敛因子，表达式如下:

其中，φ=φ1+φ2＞4。

惯性加权因子w的适当选择提供了全局搜索和局部搜索的一个平衡。一般地，w可以动态设置为

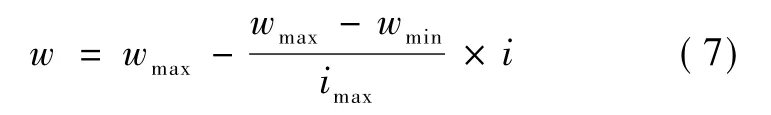
其中，imax是最大迭代次数;i是当前迭代次数;wmax和wmin是惯性加权因子的上下限。

在上述过程中，粒子速度受限于一个最大值vmax，通常设定为每一维变量动态范围的 10% ～20%。

2.2 变异

Ahmed等发现粒子群算法在早期迭代时表现很好，但是常常在接近最优解的时候出现问题，这种现象称之为停滞［23］。为了避免这种现象，Ahmed等提出了将遗传算法的变异整合到PSO中［24］

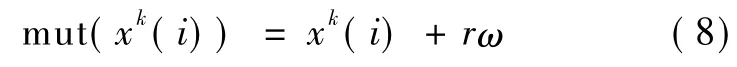
其中，xk(i)是第i代中的某一个n维粒子，x(i)= {x1(i)，x2(i)，…，xn(i)}中随机选择的一维;ω均匀随机分布于，这表示了0.1倍于搜索空间xk(i)的长度;r从{1，－1}中随机选取。

然而，从式(8)可以看到，变异空间受 ω的限制，在搜索过程中一直固定变异空间的这种做法并不是最佳的。因此，可以通过修改变异空间使其成为动态变异空间来进一步改进算法。下面介绍一种基于小波理论改变变异空间的小波变异算法。

2.3 小波变异

小波变异(Wavelet Variation)显示了更强的搜索能力［25］。小波变异的具体操作如下:种群中的每个粒子都有机会变异，设变异概率为pm(pm∈［0，1］，用户自定义)。在操作时，每个粒子都产生一个介于［0，1］之间的随机数。如果它大于或等于 pm，则该粒子发生变异。例如，假设选中的变异粒子为x(i) = {x1(i)，x2(i)，…，xj(i)，…，xn(i)}， 而xj(i)为随机选中的变异元素，它的变异空间为，则变异之后的粒子为

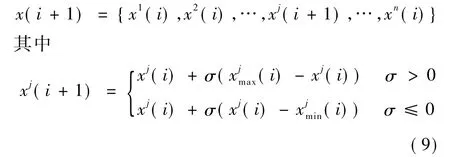
若用小波函数作为母函数的话，则有

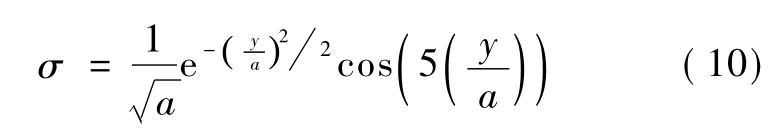
从式(10)看出，如果σ→1，则变异元素xj(i)将达到最大值;如果 σ→－1，则变异元素xj(i)将达到最小值)。值越大，搜索空间越大;值越小，搜索能力越强。

在整个进化过程中，总的正变异与总的负变异几乎是一样的，如此则提供了很好的稳定性，这是因为标准差会很小。由于小波函数99%的能量都集中在区间［－2．5，2．5］中，因此自变量y可以随机地从区间［－2．5，2．5］×a中选取。为了获得更好的搜索能力，伸缩因子a可以设定为t/T的函数，其中t为当前迭代数，而 T为总迭代数。进一步为了使得迭代早期搜索空间增大以增强变异效果，而到迭代后期搜索空间减小，这里给出一个伸缩因子a 随t/T的单调递增函数，即

其中，β是形状因子;g是伸缩因子的上限。

从式(11)可以看出，迭代次数t/T增大，则伸缩因子a增大，于是根据小波函数式(10)，则σ减小，也就是变异空间减小，削弱了变异效果。

综上，小波变异带来的效果是，当迭代次数很小的时候，例如t/T=0时，根据式(11)推知，伸缩因子a=1，于是变异空间为小波母函数的上下限值;随着迭代次数t/T的增加，仍然根据式(11)可知，伸缩因子a增大，故根据式(10)得:变异空间减小为小波母函数的。以下将含小波变异的PSO简记为WPSO。

2.4 算法实现

求解约束优化问题常用的方法是增加一个惩罚函数。通过惩罚约束项，约束问题可以转化为非约束问题，原问题变为一个单一的目标函数，这样便可以利用非约束优化算法求解该目标函数。利用惩罚函数，式(1)的优化问题可以一般化为

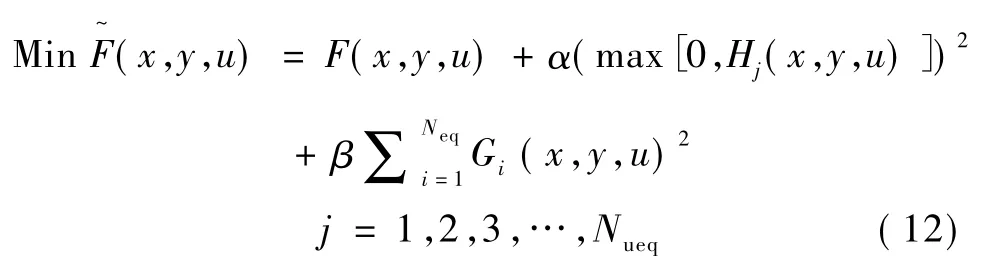
其中，F～(x，y，u)是用于评价种群中个体适应值所采用的惩罚函数;α和β均为惩罚因子。由于等式约束Gi已经隐含于算法中的潮流计算(本文采用BPA)，因此可以在评价函数F～中省略。所以也没有必要为惩罚因子β赋值，于是评价函数变为:

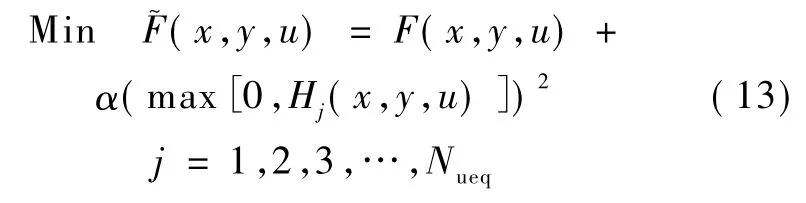
针对那些违背约束的解，如果可以引入足够的惩罚，也就没有必要给出精确的α，另外，也没有必要为不同类型的约束设置不同的惩罚因子，一般来说，α= 1000已经足够。

WPSO的计算流程为在 SPSO的基础上增加一步小波变异操作即可，具体如下:

第一步，输入PSO参数、系统数据、可信故障集以及每个控制变量的上下限。在满足各自上下限的前提下，随机产生一代粒子，即初始化种群。

第二步，对于每一个粒子，在给定一组控制变量的前提下，进行一次考虑PV节点的无功功率上下限的潮流计算。

第三步，将控制变量写入程序，针对可信故障进行一次为期10s的暂态稳定计算，进而根据评价函数式(13)计算每个粒子的费用。

第四步，种群中粒子均与相应的上一代比较各自的费用，找出各自的历史最好位置，并计入 pbest，pbest中最优的那个粒子即为 gbest。

第五步，如果满足任何一个终止条件，则转第八步;否则增加迭代次数。

第六步，根据式(7)更新惯性加权因子w;根据式(5)更新每个粒子的速度和坐标，如果达到了各自上(下)限，则将该速度v和坐标x设置为相应的上(下)限;根据式(9)执行小波变异操作。

第七步，转第三步并利用更新后的坐标x(即控制变量)重复上述过程。

第八步，最后一代的gbest便是全局最优解。

3 仿真算例

研究对象为2008年特高压交流试验示范工程中四川水电外送的局部决策。特高压电网南送大方式下四川电网外送潮流图如图1所示。全网有可控发电机组886台，其中四川境内有108台，为研究方便，本文只对不小于100MW的大机组进行控制，共有54台，也就是说，一个粒子的维数为54。优化求解参数见表1。

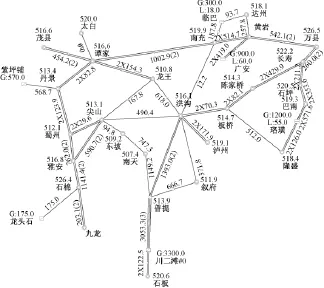
图1 2008年南送大方式下四川电网外送潮流图Fig．1 Sichuan power grid

表1 优化求解参数设置Tab．1 Parameters of optimal solution

具体设置故障为500kV线路三相短路跳双回故障:500kV线路0s发生三相短路，0.09s近故障侧开关动作，0.10s远故障侧开关动作切除本线路，同时切除并列的另一回线路。

为了加快仿真速度，本文采用试算法结果作为第一代粒子。由于切机措施是采取整机切除，因此，每台机组的控制变量只能是0或者1，在迭代过程中，若出现了小数，则采取四舍五入的方法，从而保证在下一次迭代开始前控制变量仍然是0或者1。

经过BPA对特高压试验示范工程的计算分析，得知三个特高压变电站节点晋东南、豫南阳和鄂荆门为全网的电压最低点，因此选择这三个点为暂态电压的监测点，另外，由于电压稳定与故障点密切相关，监测点还应包括川二滩、川菩提及川洪沟节点。

受限于顺义 N－1故障，晋东南南送功率最高为2800MW，本文采用南送功率递减100MW直至2400MW共5种潮流，针对两级二滩外送断面(二滩—菩提和菩提—洪沟)在首端实施三相短路故障，在0.30s采取切机措施，并进行仿真计算，得到了四川水电外送安控措施与特高压示范工程南送潮流和故障点的二维切机策略表，见表2。

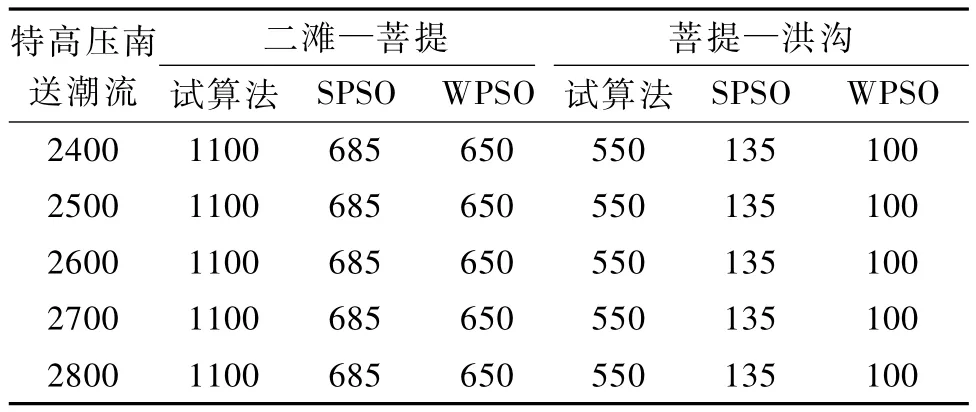
表2 二滩外送断面在N－2故障下的切机地点及切机容量计算结果(MW)Tab．2 Results of optimal combination of generator tripping under N－2 fault for section Ertan(MW)

由表2可以看出，WPSO可以给出比SPSO和试算法更好的优化结果。图2给出了特高压南送潮流2800MW二滩—菩提首端N－2三永短路故障及特高压南送潮流2400MW菩提—洪沟首端N－2三永短路故障的收敛曲线。另外，针对二滩—菩提首端N－2故障，图3～图5分别给出了不切机、切两台二滩机组以及切一台二滩机组和一台攀钢机组的监测点电压，可以看出，切一台二滩和一台攀钢机组已经可以保证故障后10s内回到0.80以上，满足暂态电压的要求，关于暂态功角的摇摆曲线类似，限于篇幅，这里不一一画出。

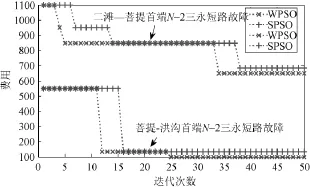
图2 WPSO的收敛曲线Fig．2 Convergence curves of WPSO

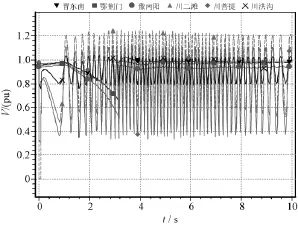
图3 二滩—菩提首端N－2故障的监测点电压Fig．3 Monitoring point voltage under N－2 fault for starting-end of section Ertan－Puti

图4 二滩—菩提首端N－2故障切两台二滩机组的监测点电压Fig．4 Monitoring point voltage under N－2 fault for starting-end of section Ertan－Puti after 2 generators of Ertan tripped

4 结论

混成粒子群优化算法求解特高压电网1000kV 与500kV协调优化控制问题取得了很好的效果，由于在实际应用中一般不允许切负荷，因此本文只建立了切机控制的优化函数，但是本文建立模型与求解方法可以很容易拓展到包含串补容性电抗、并联电抗器感性电抗以及切负荷比例因子等控制变量的优化问题。

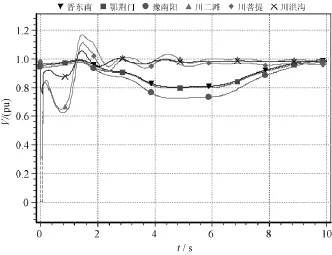
图5 二滩—菩提首端N－2故障切除一台二滩机组和一台攀钢机组的监测点电压Fig．5 Monitoring point voltage under N－2 fault for startingend of section Ertan－Puti after one Ertan generator and one Pangang generator tripped

需要指出的是，本文所提粒子群优化算法计算时间较长，一般比较适合于离线应用。但随着大规模并行计算的发展，在线应用也将成为可能，这也将是我们下一步的工作重点。

［1］DL755－2001，电力系统安全稳定导则 (Guide on security and stability for power system)［S］．北京:中国电力出版社 (Beijing:China Electric Power Press)，2001．

［2］吴国丙，吴烈鑫，张荫群，等 (Wu Guobing，Wu Liexin，Zhang Yinqun，et al．)．广东电网安全稳定控制系统的功能配置和控制原则 (Function disposition and control principle of security and stability control system for Guangdong power grid)［J］．广东电力 (Guangdong E-lectric Power)，2006，19(2):1-4．

［3］张敏，黄翠莲，杨毅斌 (Zhang Min，Huang Cuilian，Yang Yibin)．FWK-C安全稳定控制系统在梅州电网的应用 (Application of FWK-C type safety stability control device in Meizhou power grid)［J］．广东输电与变电技术 (Guangdong Power Transmission Technology)，2007，(3):63-65．

［4］Daniel R V，Pavella M．A comprehensive approach totransient stability control［J］．IEEE Trans．on Power Systems，2003，18(4):1446-l460．

［5］黄志龙，李德胜，尹凡 (Huang Zhilong，Li Desheng，Yin Fan)．北仑电厂安全稳定切机装置的功能与实现(Functions of safe and stable unit trip devices of Beilun Power Plant and their realization)［J］．华东电力 (East China Electric Power)，2007，35(7):33-36．

［6］潘东省，周海成，孙士云 (Pan Dongsheng，Zhou Haicheng，Sun Shiyun)．怒江电网2010年丰大切机方案(Over frequency generator tripping project research of the Nujiang electric power grid in 2010 high flow period operations)［J］．科学技术与工程 (Science Technology and Engineering)，2011，11(3):598-601．

［7］梅生伟，刘锋，薛安成 (Mei Shengwei，Liu Feng，Xue Ancheng)．电力系统暂态分析中的半张量积方法(Semi-tensor product approach of power system transient analysis)［M］．北京:清华大学出版社 (Beijing:Tsinghua University Press)，2010．

［8］张雪敏，梅生伟，卢强 (Zhang Xuemin，Mei Shengwei，Lu Qiang)．基于功率切换的紧急控制算法研究(Study on emergency control algorithm based on power switching)［J］．电网技术 (Power System Technology)，2006，30(13):26-31．

［9］任伟，房大中，陈家荣，等 (Ren Wei，Fang Dazhong，Chen Jiarong，et al．)．大电网暂态稳定紧急控制下切机量快速估计算法 (A fast algorithm to estimate generation capacity tripped by emergency control for transient stability of large power system)［J］．电网技术 (Power System Technology)，2008，32(19):10-15．

［10］李威，徐泰山，郑亮 (Li Wei，Xu Taishan，Zheng Liang)．电网多区域安全稳定紧急控制在线预决策系统(On-line pre-decision system for multi-area emergency control)［J］．电网技术 (Power System Technology)，2006，30(Suppl．):234-237．

［11］任伟，房大中，陈家荣，等 (Ren Wei，Fang Dazhong，Chen Jiarong，et al．)．基于最优控制原理的电力系统紧急控制及应用 (Optimal control theory based power system emergency control and its application)［J］．电网技术(Power System Technology)，2009，33(2):8-13．

［12］王安斯，罗毅，涂光瑜，等 (Wang Ansi，Luo Yi，Tu Guangyu，et al．)．基于模糊风险分析的紧急控制实时启动方法 (Real-time initiation approach of emergency control based on fuzzy risk analysis)［J］．电工技术学报(Transactions of China Electrotechnical Society)，2010，25(8):138-144．

［13］徐箭，陈允平 (Xu Jian，Chen Yunping)．基于动态安全域的电力系统暂态稳定预防控制、紧急控制及其协调 (Coordination between preventive control and emergency control for transient stability of power system based on dynamic security region)［J］．电力自动化设备 (E-lectric Power Automation Equipment)，2009，29(8): 1-7．

［14］谢欢，张保会，沈宇，等 (Xie Huan，Zhang Baohui，Shen Yu，et al．)．基于WAMS的电力系统暂态紧急控制启动方案 (Designing a start-up scheme for power system transient emergency control based on WAMS)［J］．电网 技 术 (Power System Technology)，2009，33 (20):59-64．

［15］王彪，方万良，罗煦之 (Wang Biao，Fang Wanliang，Luo Xuzhi)．紧急控制下最优切机切负荷方案的快速算法 (A fast algorithm of optimal generator and load shedding for emergency control)［J］．电网技术 (Power System Technology)，2011，35(6):82-87．

［16］Kennedy J，EberhartR．Particleswarm optimization ［A］．IEEE International Conference on Neural Networks-Conference Proceedings［C］．Perth，Australia，1995. 4:1942-1948．

［17］Wang Yihong，Wang Yingying，Chan Ka Wing，et al．Dynamic voltage security constrained optimal coordinated voltage control using enhanced particle swarm optimization ［J］．IET Generation，Transmission ＆ Distribution，2011，5(2):239-248．

［18］王义红，梅生伟，陈家荣 (Wang Yihong，Mei Shengwei，Chan Ka Wing)．考虑动态电压安全约束的预防控制粒子群优化算法 (Dynamic voltage security constrained preventive control using particle swarm optimization)［J］．电力系统自动化 (Automation of Electric Power Systems)，2008，32(12):1-6．

［19］舒隽，张粒子，黄弦超 (Shu Jun，Zhang Lizi，Huang Xianchao)．市场环境下中长期发输电协调检修计划优化 (Mathematical model of coordinational generation and transmission maintenance scheduling in electricity market)［J］．电力系统自动化 (Automation of Electric Power Systems)，2007，31(2):27-31．

［20］Ye Bin，Zhu Chengzhi，Guo Chuangxin，et al．Generating fuzzy model for short-term load forecasting using hybrid algorithm［J］．Automation of Electric Power Systems，2006，30(2):32-41．

［21］张昌华，孙荣富，刘充许，等 (Zhang Changhua，Sun Rongfu，Liu Chongxu，et al．)．基于粒子群进化算法的极限输电容量计算方法 (Improved particle swarm optimization algorithm and its application in power system transfer capability calculation)［J］．电力系统自动化(Automation of Electric Power Systems)，2007，31(7): 20-23．

［22］刘自发，葛少云，余贻鑫 (Liu Zifa，Ge Shaoyun，YuYixin)．基于混沌粒子群优化算法的电力系统无功最优潮流 (Optimal reactive power dispatch using chaotic particle swarm optimization algorithm)［J］．电力系统自动化 (Automation of Electric Power Systems)，2005，29 (7):53-57．

［23］Eberhart R C，Shi Y．Comparison between genetic algorithms and particle swarm optimization，evolutionary programming VII［M］．New York:Springer-Verlag，Lecture Notes in Computer Science，1998．611-616．

［24］Ahmed A A E，Germano L T，Antonio Z C．A hybrid particle swarm optimization applied to loss power minimization［J］．IEEE Transactions on Power Systems，2005，20(2):859-866．

［25］Ling S H，Iu H H C，Chan K Y，et al．Hybrid particle swarm optimazation with wavelet mutation and its industrial applications［J］．IEEE Transactions on Systems，MAN，Cybernatics，part B:Cybernatics，2008，38(3): 743-763．

Emergency control for transient stability of power system based on WPSO

WANG Yi-hong1，QIN Xiao-hui1，ZHOU Qin-yong1，WANG Yi-bing2
(1．China Electric Power Research Institute，Beijing 100192，China; 2．Institute of Nuclear and New Energy Technology，Tsinghua University，Beijing 100084，China)

When wavelet variation operation is increased on the basis of standard particle swarm optimization algorithm(SPSO)，an innovative hybrid particle swarm optimization algorithm(WPSO)is formed．Based on the WPSO，aiming to the UHV power system containing 1000 kV and 500 kV lines，we can carry out the coordination optimization of emergency control for transient stability problem，here，the transient stability includes transient voltage stability and transient power angle stability．Then we give a generator tripping strategy table for different UHV power flow section．The proposed WPSO-based approach has a better global convergence property and can obtain a higher quality of the optimal solution．Simulation results in the testing and demonstrating project of UHV power system show the effectiveness of the proposed approach．

particle swarm optimization;wavelet variation;transient stability;emergency control

TM72

A

1003-3076(2014)04-0041-07

2013-02-26

国家电网公司科技项目(XT71-10-008)

王义红(1981-)，男，山西籍，工程师，博士，研究方向为电力系统规划、分析与控制;秦晓辉(1979-)，男，山西籍，高级工程师，博士，研究方向为电力系统规划与仿真，控制与保护、WAMS的高级应用。