高效浓缩池斜管的特性参数（s）与斜管中的雷诺数（Re）

（武汉电力设备厂技术中心，湖北 武汉 430064）

高效浓缩池斜管的特性参数（s）与斜管中的雷诺数（Re）

吴 林

（武汉电力设备厂技术中心，湖北 武汉 430064）

本文主要研究了高效浓缩池斜管的特性参数（s）与斜管中的雷诺数（Re）。分析了斜管沉淀原理中，雷诺数性质和特性参数公式、斜管里雷诺数Re的实例计算，探讨了斜管式浓缩机选型里，雷诺数两个概念的运用和经验公式。

高效浓缩池；斜管的“特性参数（s）”；斜管的“雷诺数（Re）”；斜板、斜管的沉淀原理；斜管浓缩机选型

普通浓缩池里的沉清水，通过“上向流”池型结构，将工业废水沉清后引入溢流堰。在沉清池的上部水域加入蜂窝形状的斜管，就构成了高效浓缩池（见图一）。由蜂窝管所形成的二次沉淀区，俗称：浅层沉降区；在二次沉淀区下部是由普通浓缩池构成的一次沉降区域。流体穿过斜管区做“上向流”运动，其间悬浮物颗粒沉积在斜管壁后，滑落至池底，用机械耙收集由底孔排出，澄清水漫入溢流堰。

从流体理论上去观察，若干根直径相同组成蜂窝状的斜管，其“湿周”量求和数，远远大于一次沉淀区池径的“水力湿周”量；这使得流径该池的过水断面发生了相对改变！意味着相对没有加入斜管浓缩池而言，其吸纳流体量扩大。根据流体介质悬浮物重力沉降的理念，在浓缩池里处于“上向流”的流体，愈趋于层流态时，其悬浮物的沉淀效果愈好。“1904年，哈镇（Hazen）根据实践经验首先提出：在沉淀中分散的非结绒颗粒的沉降效率，是以颗粒的沉降速度与池子面积为函数，而与深度、时间无关”的理论。本文以这一理念为指导，探讨斜管非几何条件和给定其几何条件里与雷诺数的关联。从而认知高效浓缩机选型设计的一般规律，笔者认为很有必要。

（一）斜管沉淀原理中，雷诺数性质和特性参数公式

（1）圆形斜管内做层流运动的流体，其宽泛化雷诺数非几何条件下的概念

图（二）表示一束二次沉淀区的斜管束，单根斜管里，过流截面直径d2，令：d2=d时，过流面积记为：

其湿周x=π⋅d，因此单根斜管水力半径R′记作：

再去引入雷诺数性质，得出下式：

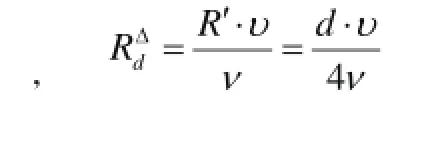
记作（1）式即得。所以工程上，采用雷诺数性质通式去比上（1）式，即为：

于是有斜管里雷诺数量级分析式，为：

式中：Re工业纯水在层流及紊流分界点的雷诺数值；

根据《流体力学》理论，工业纯水做层流与紊流临界点雷诺数Re=2320（无量纲）数。去代入斜管里雷诺数量级分析式中，即：

综上所述产生结论：在加入蜂窝状斜管里，以工业纯水层流及紊流雷诺数临界值为参照物；非几何条件所描述斜管中的运动流体，其“雷诺数”量级在RΔe=580以内。

（2）单根圆形斜管里，特性参数（s）公式的产生

由前面图（二）中某单根斜管底部，做图（三），流体介质做上向流动，在管内悬浮物（p点）的速度分别为下述。

u指：水流的局部流速（散流线）。sυ指：颗粒沿铅直（重力场）方向水力沉速。pυ指：颗粒在斜管里的理论沉降速度。θ指：斜管（或斜板）的倾角。α指：斜管（或斜板）与铅垂线夹角。d指：单根斜管的直径。

根据运动学原理，颗粒在斜管内理论沉速等于水流速度与颗粒铅直沉速的矢量和。

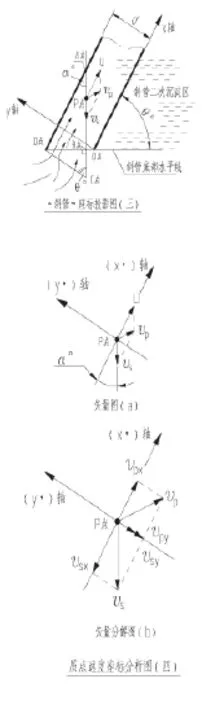
用以描述颗粒（悬浮物）沿铅直方向速度sυ的分解式。

同理，将pυ去在自然座标系上投影分解，并注意到水流速度u⇀在微积分学里，视为变数处理，省略矢量符号记法。同时沿自然座标系指向的逆向参数为负值，那么矢量分解为：

再代入颗粒（质点）沿铅直方向速度分解式。则：

产生颗粒理论沉速的自然座标上分解式。

根据速度

微分性质。

定义：质点（或动点）的速度在座标轴上的投影，等于该点的位移对时间的一阶导数（或微商）。

分别得式。

去将这两个式子做比式，那么有：

将sυ，θ看做常数。而u及x，y去视为变数，去分离变量建立微分方程。

在等式两边取不定积分。解这个等式两边积分，保留着一个积分项得出：

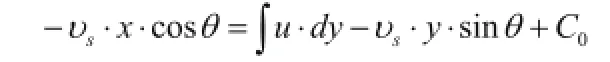
去令：质点的位移y与管径的“比例函数Y”记为：

并且令：质点的位移x与管径的“比例函数X”，记为：

引入“线性比例函数符”代换为：

在这个变形式基础上，将各项去除以管内的平均流速0υ参数，整理出下式：

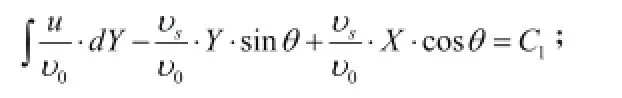
编号（2式）

称之为层流态里斜管（或斜板）内颗粒沉降轨迹一般公式。在积分号里两个速度参数的含意：u指圆管横断面法线上分散轴向流速。0υ指圆管横断面法线上的平均流速。

当流体在均直圆管中做等速运动时，速度u和切应力τ都将对称分布于管轴为中心轴的圆柱面上。由牛顿的内摩擦定理，给出图（六）的剪应力微分式。

式中：γ指流体重度；R′指水力半径；J指水力坡度。

得微分方程。

那么γ，J，μ为常量；u，y′为变数。分离变数后再取不定积分，即：

不定积分解式。

由图（六）可知，分散的轴向流速线在边界上u=0性质存在。取边界条件解出积分常数，即：

整理为下式：

称之为：图（六）的分散轴向流速，（a）式。

摘取图（五）里“比例函数Y”的导入概念，去考察图（六）内散流线时：

得出表达式：用以描述比之函数Y及管径d，在图（六）里y 轴上一条任意流线的过流半径y′座标。

在《流体力学》里，给出圆管平均流速积分性质

可导出下式（见下图）。即：

式中：积分推演过程省略。ρ流体密度，g重力加速度；hw总的水头损失；d圆管直径；μ流体动力粘性系数；l所研究流体上，由1～1断面至2～2过流断面间长度。

且有γ=ρ⋅g及hw=J⋅l去代换上式，则有：

记为（c）式。

……

去将（b）式与（c）式做比式，最后整理为：

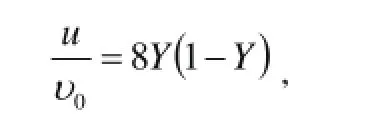
记做（d）式。其参数含意同前所述。经前述推演得出编号（2）式，重摘：

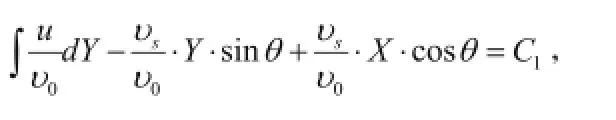
“编号（2）式”。

取（d）式去代换“编号（2）式”

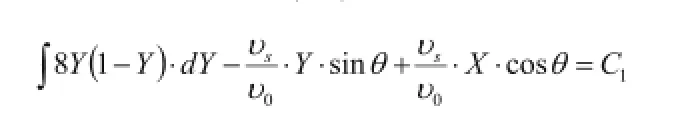
给出。或：

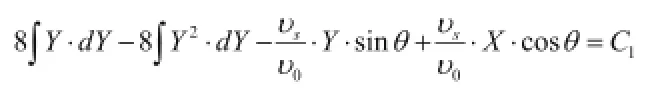
展开式。

去解为：

根据图（五）几何条件及比之函数，当X=L，Y=0时，解出边界常数C1式。

即：

回代积分常数，得到变形编号（3）式。即：

编号（3）式。

在（3）式里，已含有三个“比例函数”。即：

是任意座标值与管径的函数，观察图（五）去考察颗粒在斜管B′点，沉淀开始发生的条件。取B′点座标

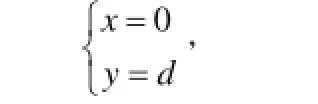
用“比例函数”量，讨论边界条件：

表7 -1

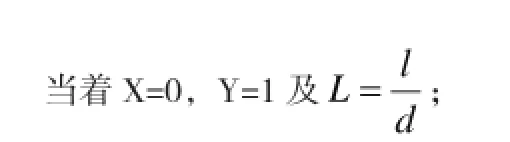
再代入编号（3）式。则有

取符号s描述该式，又记为下式。

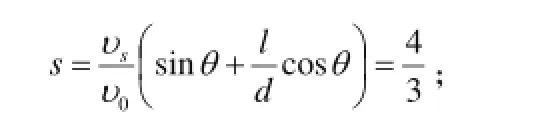
记为编号（4式），圆形斜管特性参数公式。

式中：sυ——悬浮物颗粒的水力沉速；0υ——管内的平均流速；θ——斜管与水平面的夹角（或称：倾斜角）；l——斜管的长度；d——斜管的直径；

（二）斜管里雷诺数Re的实例计算

（1）计算的输入条件

单根斜管直径d=80mm，长度l=1m，倾斜角θ=60°；若干根构成蜂窝管面。摘录由：西南电力设计院主编《火力发电厂除灰计算手册》里，粉煤灰的水力沉速实例参数的数据表1如下。选取北京热电厂1:10参数组里，sυ=0.540（mm/s）值。

（2）根据编号（4）式，求取斜管中的平均流速0υ值

已知：d=80mm，l=1000mm，

θ=60°，sυ=0.540（mm/s）。

依编号（4）式，即：置。斜管的加入使沉淀池理论沉降面积增大，而实际池子投影面积并没改变。设计选型中，常常与不加斜管的普通大沉降池面积做比较，可以采用以下等式分析。即：

（3）根据雷诺数公式，求取斜管里给出条件下的Re值

已知：圆管内平均流速0υ=2.8819（mm/s），管径d=80（mm），以工业纯水的运动粘度系数v=10-6（m2/s）为参照。

做单位换算：0υ=2.8819×10-3（m/s），d=80×10-3（m）。

依雷诺数公式：

式中：A1x——n根斜管沉淀面积总和（m2）；F——不加斜管普通浓缩池沉淀面积（m2）；

[例题]：

某高效浓缩池直径D=20m，采用直径d=80mm，蜂窝管构造二次沉淀区。已知斜管水平投影理论面积A1x=2443.75m2，其雷诺数=230.552值，且有=580（无量纲）量级内为流速条件。这种斜管式浓缩机等效于多大系列的普通浓缩机？……计算结果，等效普通浓缩池面积F=971.4m2值。参照《火力发电厂除灰计算手册》“表7-2”，可等效为一台直径约φ35米的普通浓缩池。

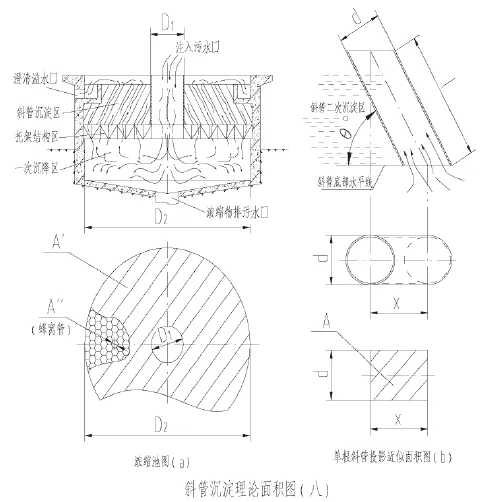
高效浓缩机的选型设计，当确定了斜管几何条件下的雷诺数值，常常需要对斜管区理论沉淀面积做近似计算，完成雷诺数（，）两个概念具体应用。沉淀斜管区理论沉淀面积，由以下几个公式组成，参见图八。左图（a）里，浓缩池内径D2，被桁架所支承的稳流筒内直径D1；A′表示浓缩池内直径投影面积；A

于是，使用上述给定计算条件下，经引入斜管特性参数公式求出雷诺数值，并用符号表示算值代号。同样去采用符号表示层流态斜管宽泛化雷诺数来区别这两个概念。（=580[无量纲]值）。

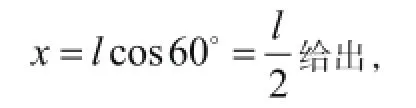
所以单根斜管投影面积近似记做：

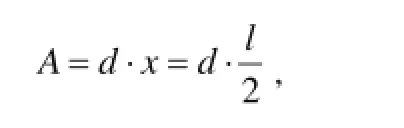
且θ=60°；又取图（a）里，浓缩池投影面积去记为：

仍取图（a）里，斜管出水口的投影圆面积A′′，并与A′做比式，求取浓缩池内斜管总根数近似值。即：

若用A1x表示普通浓缩池内加入斜管的理论沉淀面积之总和，必等于单根斜管的投影面积（A）与总根数（Z）之乘积，去代入上述几个算式，记作：

在（e）式里参数含意：A1x——斜管区理论沉淀面积（m2）；l——单根斜管的长度（m）；θ——斜管与水平面夹角（度）；D2——浓缩池内直径（m）；D1——稳流筒（结构）的直径（m）。

[算例]：

已知某高效浓缩池的几何参数为：l=1m，d=80×10-3m， θ=60 °；D2=20m，D1=3m值，求加入斜管区域里，其斜管沉淀理论面积？

代入（e）式计算：

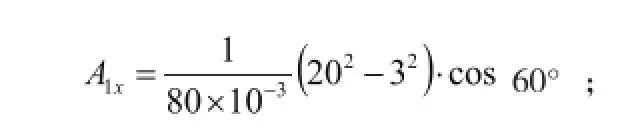
A1x=2443.75m2为所求。

上述计算结果，由于符合在层流态斜管里，按雷诺数两个概念建立的等式性质，便涵盖了高效斜管式浓缩机选型设计的一般规律。

[1]上海市政设计院．斜板、斜管沉淀原理及技术[M]，1975．

[2]江宏俊．流体力学[M]，1985．

[3]黄文锽．水力学[M]，1981．

TD92 < class="emphasis_bold"> 文献标识码：A

A