铁路牵引供电系统设计中的谐波谐振分析及抑制方案研究

蒋功连

(中铁第一勘察设计院集团有限公司电化处，西安 710043)

近年来交直交型电力机车(含动车组)得到广泛应用，相比交直型电力机车，具有牵引功率大、谐波电流综合畸变率小、功率因数高等技术优势，但注入牵引供电系统的谐波频谱变宽，高次谐波电流不容忽视，容易引起系统谐波谐振［1］。现场已经发生多起谐波谐振事故，造成过电压保护动作，断路器跳闸，保护器、避雷器等设备烧损甚至爆炸，并联补偿装置无法正常运行，对供电可靠性带来了一定程度的影响［2，3］。

当前电力系统在谐波源建模、谐波潮流计算以及谐波抑制措施方面开展了深入的研究，取得了一系列研究成果，值得参考和借鉴［4，5］。牵引供电系统采用单相工频供电模式，牵引网为多导体传输线结构，运行方式存在多样性，移动式牵引负荷既是功率源又是谐波源［6］。针对牵引供电系统的特殊性，有必要在设计阶段对系统谐振特性与变化规律进行理论分析，有针对性地提出抑制措施。

本文基于四象限变流器拓扑结构与控制策略，构建电力机车谐波源特性模型，基于多导体传输线理论与链式网络模型，构建牵引供电系统数学模型，利用MATLAB/Simulink仿真平台，研究牵引供电方案与运行方式对系统谐波谐振特性与变化规律的影响，给出便于工程应用的无源滤波器设计方案，仿真验证了该方案的正确性与有效性。

1 交直交型电力机车(动车组)谐波建模

当前我国交直交型电力机车(动车组)主要采用四象限变流器，以CHR2型动车组为例，其采用单相三电平四象限变流器拓扑结构，如图1所示。

图1 单相三电平四象限变流器主电路

四象限变流器能在四象限运行，通过控制电力电子开关的导通与关断，可以使变流器工作在整流与逆变两种模式下。

单相三电平四象限变流器输出电压为

式中 M——调制比;

Ud——直流侧电压;

ω——调制波角频率;

ωc——载波角频率;

B——调制波相位;

α——载波相位;

Jn(x)——n阶的贝塞耳函数;

N=ωc/ω——载波比。

对于三电平PWM变流器网侧谐波电流源iabn为

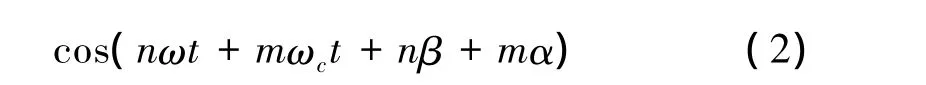
分析表明:CRH2型采用三电平PWM变流器网侧电流不存在(2k+1)N+n(k=0，1，2…，n=±1，±3…)次谐波，仅存在2kN+n(k=1，2…，n=±1，±3…)次谐波。

2 牵引供电系统建模

在电气化铁路设计阶段一般由电力部门提供外部电源电压等级和短路容量，通过三相解耦的方法可以建立外部电源谐波模型。在已知牵引变压器三相谐波漏抗阵的基础上，针对不同接线方式下牵引变电所原次边电气量变换关系，可以等效到次边牵引变压器谐波阻抗。因此，牵引供电系统建模的重点是构建牵引网谐波模型［7］。

牵引网是由馈电线、接触网、钢轨、回流线等构成的向电力机车或动车组输送电能的网络。根据采用供电方式的不同，牵引网会有不同的拓扑结构，本质上是一平行多导体的传输线结构，可以基于电磁场理论计算单位长度牵引网串联阻抗参数矩阵Z、并联导纳参数矩阵Y。图2是长度为l、含m根导线的多导体传输线等值“π”型模型，ZΠ和YΠ满足式(3)和式(4)，h为谐波次数。

图2 多导体传输线等值“π”型模型

牵引网为一平行多导体传输线系统，任一供电臂都可以从拓扑结构上构成一个链式网络。针对不同供电方式，利用牵引网自身的电气回路节点和列车运行时的实际位置对牵引网进行自然切割，图3为复线2×27.5 kV AT供电方式的供电臂链式网络模型。

3 牵引供电方案谐振特性分析

以某新建电气化铁路为例，牵引供电方案采用AT供电方式，部分区段主要技术参数如下:平均供电臂长度23.75 km、导线组合为接触线 CTS150+承力索JTM150+正馈线LBGLJ240+保护线LBGLJ120，牵引变压器采用 Vx接线方式，变压器容量为2×(25+25)MVA，系统最小短路容2 850 MVA，机车类型为CRH2型动车组，满功率运行，谐振特性观测点受电弓位置。机车分别为与距离牵引变电所5，10，23.75 km时，用阻抗测量模块对从该处向牵引网看去的阻抗-频率特性进行测量，得到各节点的阻抗-频率图，如图4所示。表1为机车位于不同位置时的并联谐振点频率和阻抗特征值。

图3 复线2×27.5 kV AT供电方式的供电臂链式网络模型

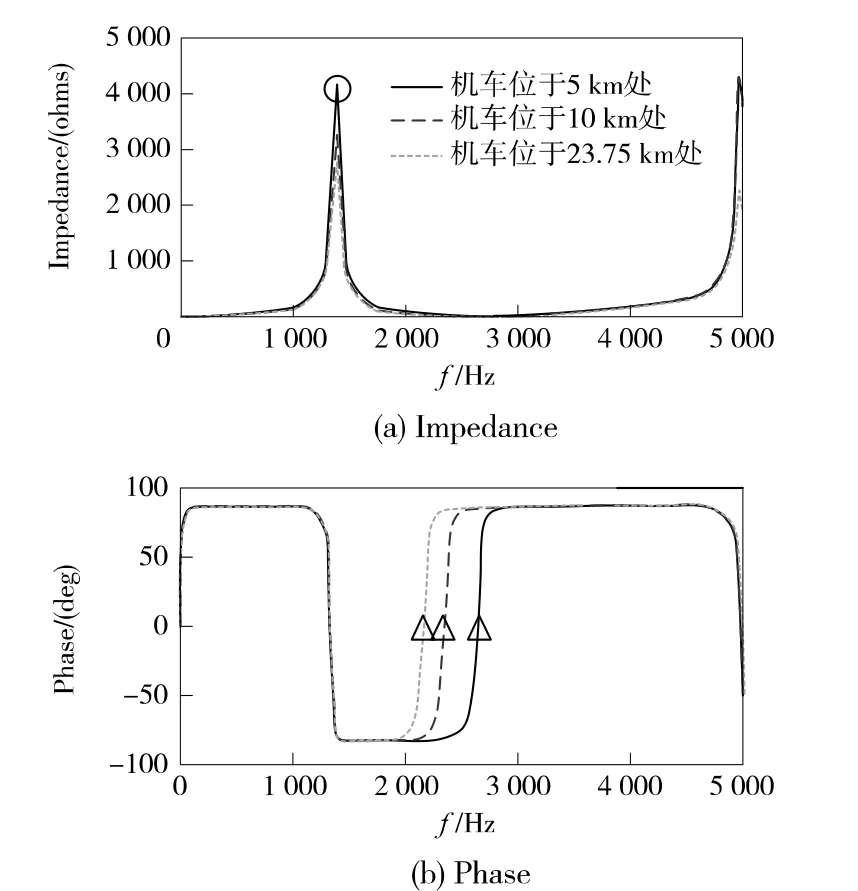
图4 动车组位于不同位置时的系统频率－阻抗特性曲线(图中○表示并联谐振点，△表示串联谐振点)

表1 动车组位于不同位置时的并联谐振点频率和阻抗特征值

由图4和表1可知，系统并联谐振频率始终是1 350 Hz(27次谐波)，即在该供电方案下，并联谐振点与机车所处的位置无关，且并联谐振点谐波阻抗最高可达4 169 Ω。系统串联谐振点却发生了显著变化，机车距离变电所越远，串联谐振点越向高频区段方向移动。

机车位于不同位置，由其发射的谐波电流在牵引网中传递，引起了牵引变电所谐波电流不同程度的放大，如图5所示。可见，当机车位于供电臂末端时(距离牵引变电所23.75 km处)，27次谐波电流放大倍数接近45倍，而机车位于牵引变电所5 km处时，放大倍数接近35倍，可见电力机车(谐波电流源)离变电所越远牵引变电所馈线位置谐波电流放大倍数越大。

图5 机车位于不同位置时牵引变电所谐波放大情况

4 越区供电模式下谐振特性分析

《铁路电力牵引供电设计规范》(TB1009—2005)明确规定:在相邻两变电所供电的电分相处应设联络开关，当需要时可实现越区供电。针对上述实例分析中的牵引供电区段，若由牵引网正常供电模式转变为越区供电，则供电臂长度延长为45.68 km，考虑其他条件不变，电力机车位于供电臂末端，分析越区供电模式下牵引供电方案谐波谐振特性的变化，图6为正常与越区供电模式下系统阻抗-频率特性对比图，表2为两种模式下机车位置处的系统并联谐振点阻抗特征值对比。

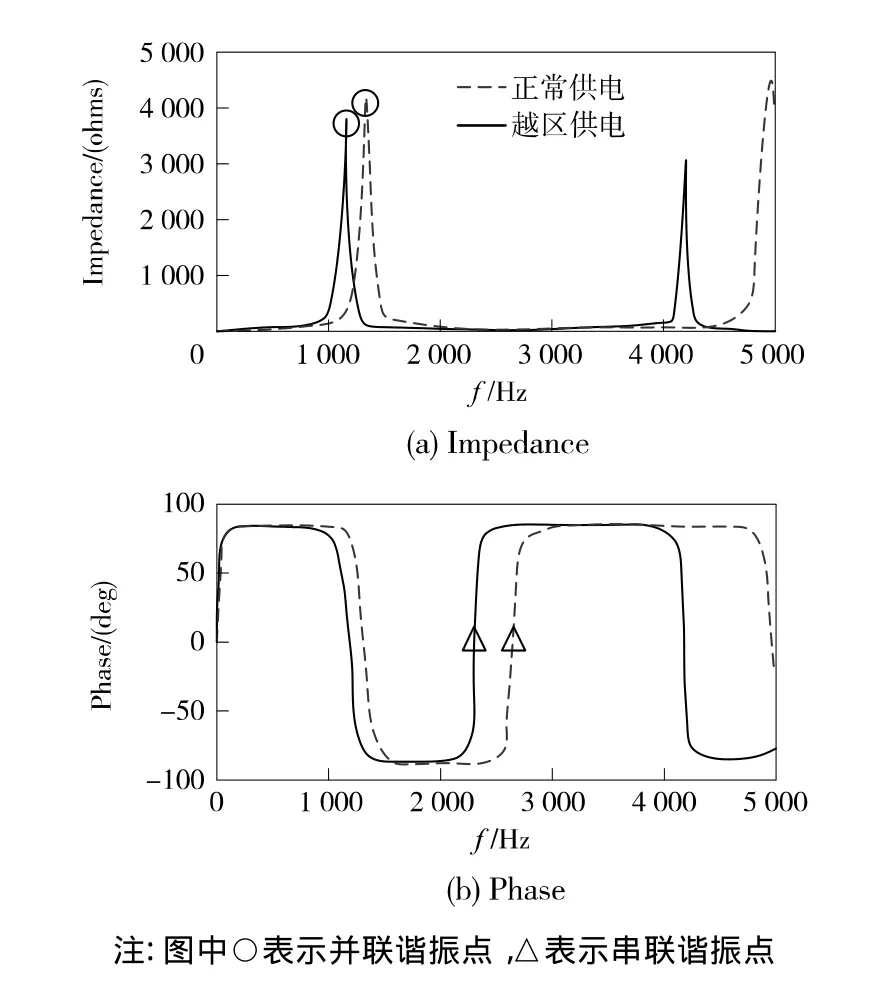
图6 正常与越区供电模式下系统阻抗－频率特性曲线

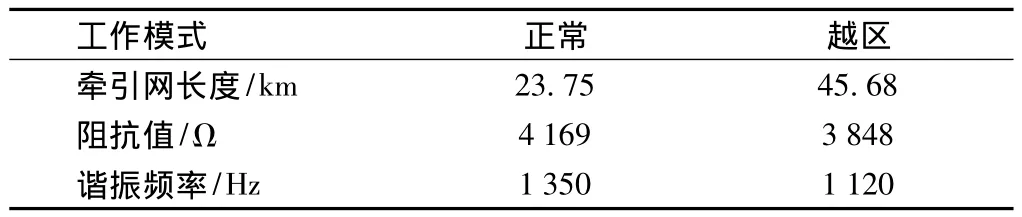
表2 正常与越区供电模式下动车组位置系统并联谐振点对应的阻抗特征值

可见，牵引供电系统由正常模式转变为越区供电模式时，系统并联谐振点由1 350 Hz(27次谐波)变化为964 Hz(约19次谐波)，即随着供电臂长度的增加，并联谐振点由较高频段向较低频段方向移动，同时系统串联谐振也发生了类似的变化。通过仿真也进一步证明，随着供电臂长度的增加，系统并联谐振点向左移动，即并联谐振点频率越低，越早发生第一次并联谐振。

结合国内主要交直交机车(动车组)的谐波电流发射特性分析［7］，可以发现无论是正常还是越区供电模式，上述谐振点均位于谐波电流含量较显著的频段，更容易造成车-网系统谐波谐振现象［9，10］。

分析不同工作模式下CRH2型动车组发射的谐波电流在牵引网中传递特性，得到了牵引变电所馈线谐波电流的放大情况，如图7所示。可见，越区供电模式下并联谐振点位置馈线谐波电流的放大倍数有所降低，这主要是由于系统谐波阻抗的变化造成的。

图7 正常与越区供电模式下牵引变电所谐波电流放大情况

当前我国推广采用基于交-直-交变流技术的电力机车(含动车组)，由于变流器控制技术、拓扑结构以及开关频率的差异，不同类型交直交型电力机车具有不同的谐波电流频谱特性。为了对牵引供电系统谐波谐振特性进行具体分析，可以参照本文方法，针对设计阶段电力机车类型，构建电力机车谐波电流发射模型;结合牵引供电设计方案，构建牵引供电系统谐波仿真模型;基于“车-网”耦合的思想，对实际牵引供电设计方案进行谐波谐振特性与变化规律的分析，提高牵引供电的安全性和可靠性。

5 谐振的抑制与仿真分析

谐波谐振对牵引供电系统的危害很大，故需要采取滤波措施进行抑制。目前，常用的滤波器分为有源滤波器与无源滤波器，由于当前大功率有源滤波器采用的开关器件(例如IGBT)无法满足滤波功能对开关频率的要求，不能有效抑制高次谐波电流。因此在电气化铁路中，推荐采用无源高通滤波器。本文采用C型滤波器，其电气结构如图 8 所示［11，12］。

滤波器设计步骤如下所述。

图8 C型滤波器模型

(1)确定串联电容器C1的容量QC1，单位为Mvar。其中电容器的电抗值满足下式

(2)一般将电感L与电容C2在基波下调节成串联谐振，将电阻R支路短路，使其上消耗的功率减小到最小，其中C2的电抗值满足下式

(3)为了滤除h次谐波，电抗器L的大小满足下式

其中，h为谐波次数。

(4)滤波器中电阻的大小满足

其中，Q为品质因数，一般取0.5＜Q＜5;Xn为特征电抗，Xn=n·XL。

(5)C型滤波器在任何h次谐波下的阻抗满足下式

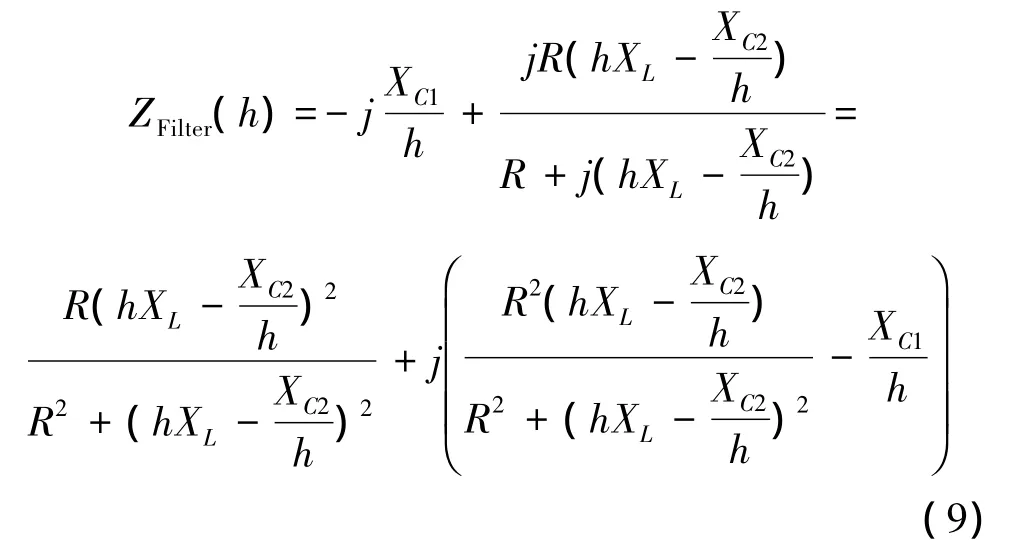
上述牵引供电系统正常运行时系统并联谐振点在27次谐波位置，设计C型滤波器参数如下，其中品质因数取 0.5，XC1=378 Ω，XC2=XL=1.05 Ω，R=80 Ω。

对比加载谐波抑制装置前后牵引变电所馈线谐波电流放大情况，如图9所示，可见C型滤波器对牵引供电系统高次谐波谐振起到了很好的抑制作用。

6 结语

图9 加载谐波抑制装置前后牵引变电所馈线谐波电流放大倍数

本文研究了采用四象限变流器的电力机车(动车组)谐波源模型及谐波发射特性，结合牵引供电系统设计方案，利用多导体传输线理论与链式网络模型，构建牵引供电系统数学模型，基于MATLAB/Simulink仿真平台，研究牵引供电方案与运行方式对系统谐波谐振特性与变化规律的影响。针对可能发生的高次谐波谐振，提出采用无源C型滤波器方案并给出了设计步骤，仿真验证了该方案的正确性与有效性，相关研究结果为牵引供电系统优化设计与安全运营提供了重要依据。

［1］李群湛，连级三，高仕斌.高速铁路电气化工程［M］.成都:西南交通大学出版社，2006.

［2］北京铁路局，北京交通大学，中铁电气化勘测设计院，中国铁道科学研究院.京秦线蓟县南牵引变电所供电区段牵引网高次谐波谐振测试分析报告［R］.北京:2007.

［3］王兰和.高次谐波对自闭供电的影响及采取的对策［J］.铁道标准设计，2005(3):85-87.

［4］杨洪耕，王磊.基于拉盖尔多项式的非线性负荷谐波发射水平估计［J］.中国电机工程学报，2005，25(7):81-85.

［5］Zhenyu Huang，Wilsun Xu，Dinavahi V R.A practical harmonic resonance guideline for shunt capacitor applications［J］.IEEE Trans.on Power Delivery，2003，18(4):1382-1387.

［6］杨少兵，吴命利.基于实测数据的高速动车组谐波分布特性与概率模型研究［J］.铁道学报，2010，32(3):33-38.

［7］姚楠.电气化铁道牵引网基波与谐波模型研究［D］.北京:北京交通大学，2008.

［8］陈民武.电气化铁路电能质量预测与对策分析研究［R］.中铁第一勘察设计院集团有限公司博士后研究工作报告.西安:2012.

［9］刘建强，郑琼林，杨其林.高速列车牵引传动系统与牵引网谐振机理［J］.电工技术学报，2013，28(4):221-227.

［10］Alberto Dolara，Moris Gualdoni，Sonia Leva.Impact of High-Voltage Primary Supply Lines in the 2×25 kV-50 Hz Railway System on the Equivalent Impedance at Pantogragh Terminals［J］.IEEE TRANSACTIONS ON POWER DELIVERY，2012，27(1).

［11］George J.Wakileh著.电力系统谐波—基本原理、分析方法和滤波器设计［M］.徐政，译.北京:机械工业出版社，2010.

［12］郭牛宝.电网电容器组谐波谐振和谐波放大的分析［J］.铁道标准设计，2002(8):65-67.