地基柔性效应对铁路连续梁桥弹塑性地震反应的影响
包宗林
(中铁第一勘察设计院集团有限公司,西安 710043)
1 概述
近十几年来,我国地震活动频繁,多次强烈地震都对铁路桥梁造成了较严重的破坏后果。桥梁作为生命线工程,是交通网络的重要组成部分,在抗震救灾中处于极其重要的地位[1-2]。震后调查结果表明[3-5],桥梁震害主要起因于下部结构。
2009年修订版《铁路工程抗震设计规范》[6](以下简称《震规》)采用多级抗震设计思想,要求采用非线性时程反应分析方法对钢筋混凝土桥墩进行弹塑性地震反应分析,并对桥墩塑性铰区的转动能力进行验算。弹塑性设计方法允许结构在罕遇地震作用下进入到弹塑性阶段,依靠结构和材料自身的弹塑性力学性能吸收地震能量,减轻地震荷载效应。
文献[7]以预应力混凝土连续梁桥为研究对象,基于纤维模型基本原理建立该桥的弹塑性分析模型,并进行罕遇地震下桥梁弹塑性地震时程响应分析。文献[8]采用塑性铰模型对某高速铁路大跨连续梁桥进行了弹塑性地震反应分析及抗震验算。文献[9]指出基础(地基)塑性的影响是重力式桥墩在罕遇地震分析中需要考虑的一个重要问题,文中从试验及理论分析两个角度探讨了基础非线性对桥梁地震反应的影响。文献[10]探讨了基础刚度对大跨度连续梁桥墩弹性地震反应的影响,结果表明基础刚度对地震反应有较大影响,设计时应力求其计算准确。
本文以某大跨度连续梁桥为工程背景,建立了考虑地基柔性约束效应的弹塑性地震反应分析模型,分析地基柔性效应对桥墩动力特性的影响,总结了地基柔性约束效应对桥墩弹塑性地震反应的影响规律,对桥墩的延性抗震设计提出了建议。
2 工程概况
某高速铁路大跨连续梁桥桥跨布置为(80+128+80)m箱梁桥,引桥为32 m预应力混凝土简支梁桥。场地类别为Ⅱ类,场地特征周期为0.4 s,设计地震下地面峰值加速度为0.13g。主梁采用C50混凝土单箱单室结构,跨中梁高为5.6 m,中墩处梁高为9.6 m,采用二次抛物线型渐变。箱梁顶板总宽13.4 m,底板总宽7.0 m。下部结构为圆端形实体桥墩(纵向尺寸及横向尺寸分别为4.5、11.6 m),基础为钻孔灌注桩(桩径为1.5 m,桩长为55 m采用行列式布置,共计24根),地基土以卵石土和圆砾土为主。桥墩及桩基础均采用C30混凝土。采用盆式橡胶支座,3号墩为固定墩。全桥总体布置如图1所示。
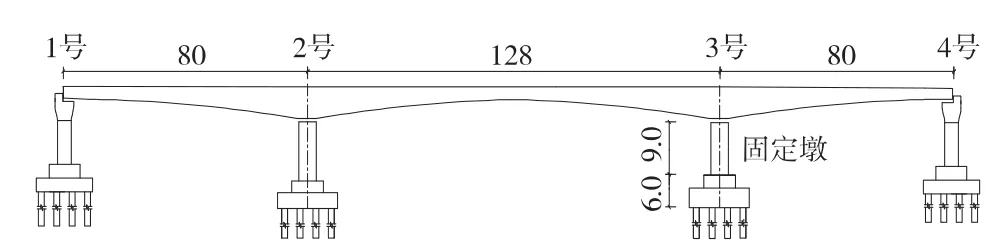
图1 全桥总体布置示意(单位:m)
由于连续梁桥在一联桥跨中通常仅设置1个固定墩。在地震荷载作用下,由于上部结构的惯性力主要由固定墩承担,因此固定墩必须满足强度及延性的要求。地震下利用桥墩发生塑性变形,延长结构周期,耗散地震能量[11]。
3 动力计算模型
本文重点研究连续梁固定墩顺桥向的弹塑性地震反应,根据《震规》规定,可以采用单墩模型代替全桥模型进行分析。固定墩的动力计算模型见图2。
(1)上部结构的模拟
上部结构仅考虑质量效应,利用集中质量单元实现,质量大小为一联梁的质量和二期恒载质量之和,二期恒载按照200 kN/m考虑。
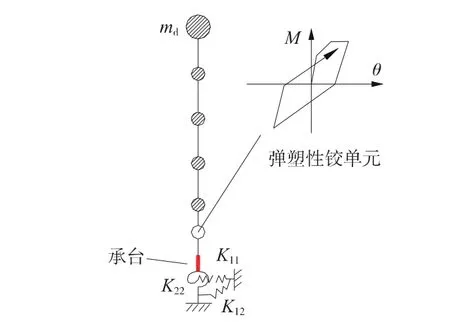
图2 动力计算模型
(2)墩柱构件的模拟
墩柱采用空间梁单元模拟,在墩底塑性铰区的非线性变形采用集中塑性铰模型模拟,塑性铰的滞回规则采用Clough模型。承台采用弹性梁单元模拟。
(3)基础柔性效应的模拟
将地基土对结构的约束作用简化成线性弹簧施加在承台底,考虑平动、转动及耦联弹簧刚度的影响。弹簧刚度的计算方法见式(1)~式(3)
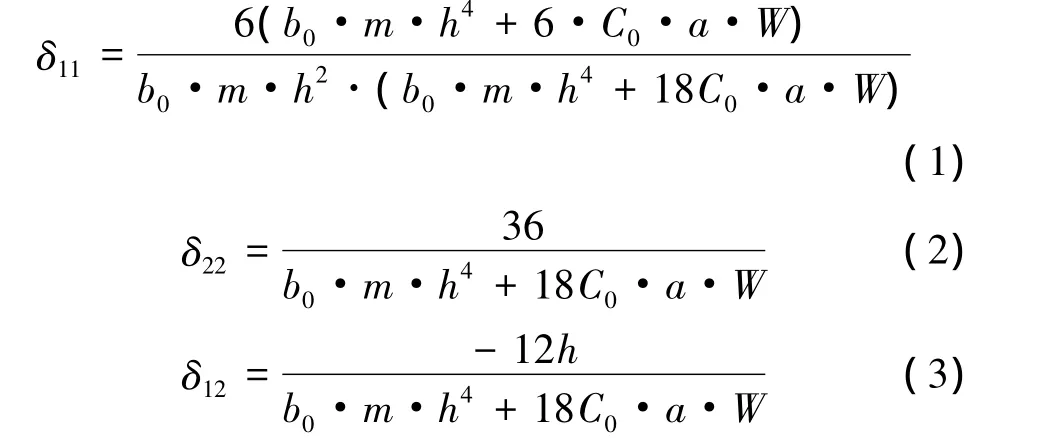
4 分析工况及对桥墩动力特性的影响
4.1 分析工况
在桩-土相互作用方面,《震规》主要采用线性弹簧模拟基础的柔性约束效应。弹簧刚度的计算方法与地基土的m值取值关系密切。但《铁路桥涵地基和基础设计规范》[12]针对卵石土,给出的m值范围覆盖较广,在30 000~80 000 kN/m4。m取值不同,对桥墩的弹塑性地震反应影响不同。为了研究m值对桥墩弹塑性地震反应 的影响,分 别取 m=10 000、30 000、50 000、80 000 kN/m4,得到的承台底弹簧刚度见表1,表中数值已考虑承台侧向土的刚度贡献。

表1 地基弹簧刚度
从表1中可以看出,随着m值的增加,基础的平动刚度数值的变化大于其转动刚度及藕联刚度,即m值的改变对基础平动刚度影响较大。
4.2 桥墩动力特性分析
桥墩的动力特性分析见表2。从表2可知,随着地基土由软逐渐变硬,桥墩的1阶自振频率逐渐增大,但2阶频率基本未变。

表2 桥墩动力特性 Hz
5 弹塑性地震反应分析
5.1 输入地震动及求解方法
输入桥址场地安评报告提供的50年超越概率为2%的3条地震波,峰值加速度PGA=0.21g。其中一条典型的加速度时程曲线见图3。
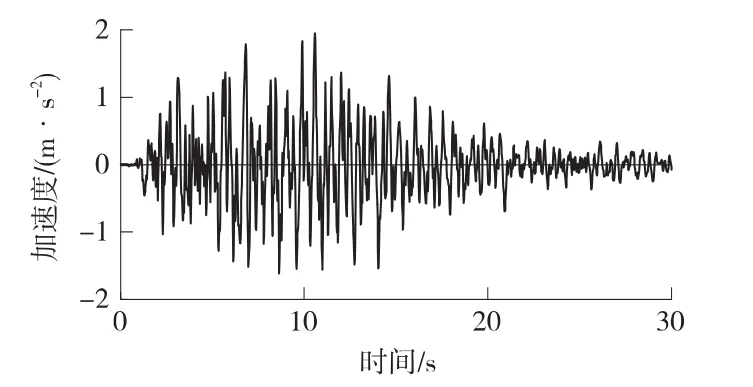
图3 典型的加速度时程曲线
结构的阻尼采用Rayleigh阻尼矩阵,应用Newmark-β法逐步积分求解,分析时间步长为0.01 s。分析时间为30 s。
5.2 桥墩的弹塑性本构关系
钢筋的应力-应变关系采用曲线强化模型,可以比较准确地描述钢筋的大变形特性,约束混凝土应力-应变关系曲线采用 Mander模型。3号墩的纵筋(HRB335)配筋率为0.55%,采用条带法对墩底截面的纵向进行了全过程分析,根据等能量法确定了骨架曲线上的控制点,分析结果见表3。

表3 3号墩底截面弯矩-曲率
5.3 分析结果
在各条地震波作用下,墩顶位移、墩底截面曲率及基底平动位移见表4。表中数值为3条波的均值。

表4 弹塑性地震反应分析结果
在第1条地震波作用下,当 m=10 000 kN/m3及80 000 kN/m4时,墩底截面弯矩-曲率关系滞回曲线见图4,墩顶及基底的平动位移时程曲线见图5及图6。
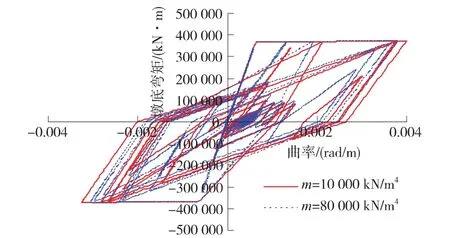
图4 墩底截面弯矩-曲率滞回曲线
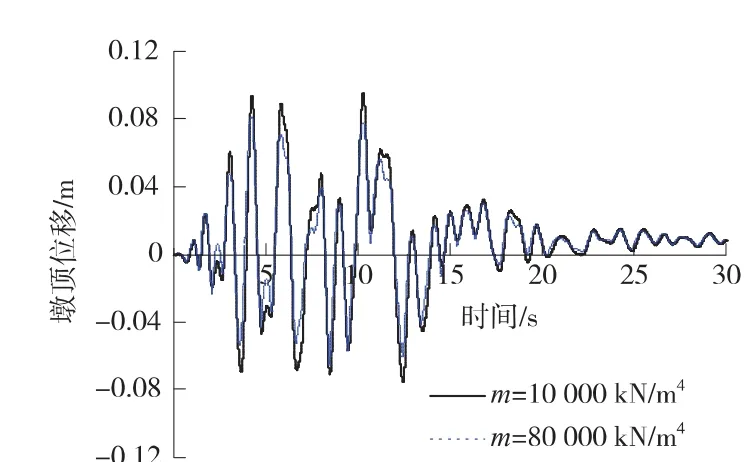
图5 墩顶位移时程曲线
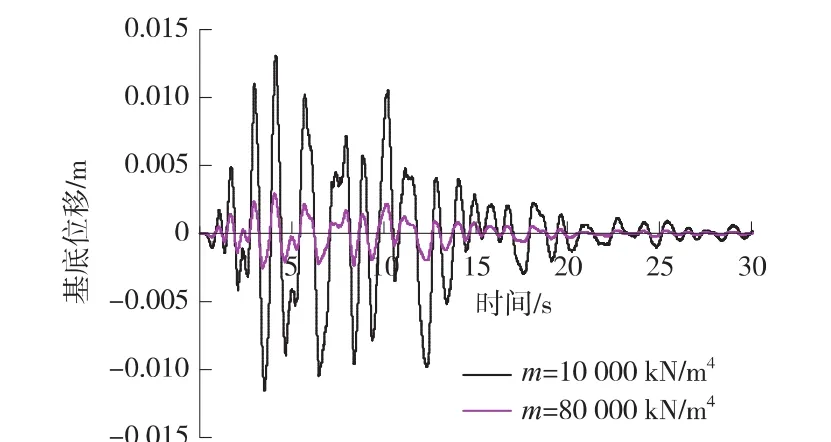
图6 基底位移时程曲线
图4~图6及表4的分析结果如下。
(1)随着地基系数m值的降低,墩顶位移及基底位移逐渐增加。
(2)随着地基系数m值的增加,墩顶位移的变化明显大于墩底截面曲率的变化。地基越软,桥墩的弹塑性地震反应有增大的趋势。
(3)为了更加合理的描述桥墩的塑性状态,建议优选墩底曲率延性指标进行评价。若选择墩顶位移作为衡量桥墩塑性状态指标,应将墩顶位移扣除相应的基础平动位移,作为桥墩发生挠曲变形产生的位移。
6 结语
通过以上分析,可以得到的结论有:
(1)随着m值的增加,基础的平动刚度数值变化大于其转动刚度及耦联刚度;
(2)m值的改变对桥墩的一阶自振频率影响较明显;
(3)随着地基系数m值的降低,墩顶位移及基底位移逐渐增加。地基越软,桥墩自身的弹塑性地震反应有增大的趋势。
为了更加合理地描述桥墩的塑性状态,建议对软土场地桩基础钢筋混凝土桥墩进行延性抗震设计时,优选墩底曲率延性指标进行评价。
[1]刘俊.长联多跨刚构-连续梁桥的抗震设计[J].铁道标准设计,2012(7):74-79.
[2]康炜.高地震区多跨长联桥梁抗震设计[J].铁道标准设计,2012(9):47-51.
[3]王克海.桥梁抗震研究[M].北京:中国铁道出版社,2007.
[4]范立础,卓卫东.桥梁延性抗震设计[M].北京:人民交通出版社,2001.
[5]王晓黎.某高速铁路连续梁桥桥墩地震反应分析[J].世界桥梁,2012,40(4):38-41.
[6]中华人民共和国住房和城乡建设部.GB 50111—2006 铁路工程抗震设计规范(2009年版)[S].北京:中国计划出版社,2009.
[7]禚一,王菲.罕遇地震城际铁路连续梁桥延性抗震设计[J].铁道工程学报,2012(4):66-72.
[8]张永亮,孙建飞,徐家林.高速铁路大跨连续梁桥地震反应分析及抗震校核[J].地震工程学报,2013,35(2):226-231.
[9]陈兴冲,夏修身,张永亮.基础非线性对桥墩地震反应的影响[J].世界地震工程,2008,24(4):25-29.
[10]颜志华.大跨度连续梁桥墩地震反应分析[J].铁道标准设计,2007(2):17-21.
[11]邓小伟.基于两水平设防的连续梁桥抗震性能分析[J].石家庄铁道大学学报,2012,25(4):39-42.
[12]中华人民共和国铁道部.TB10002.5—2005 铁路桥涵地基和基础设计规范[S].北京:中国铁道出版社,2005.

