自适应奇异值分解瞬变信号检测研究

徐彦凯 双 凯



自适应奇异值分解瞬变信号检测研究

徐彦凯*双 凯

(中国石油大学(北京)地球物理与信息工程学院 北京 102200)

该文介绍了奇异值分解检测信号的原理，研究了井下电磁脉冲数据传输中接收到的瞬变信号和噪声的奇异值分布特性，提出了相邻奇异值增量的概念，并根据瞬变信号和噪声相邻奇异值增量的不同，区分信号与噪声。在此基础上，提出了自适应选择主奇异值个数的奇异值分解检测瞬变信号的方法，并给出该方法检测瞬变信号的具体流程。仿真结果表明，与传统奇异值分解相比，该方法检测微弱瞬变信号更准确。

信号检测；瞬变信号；自适应奇异值分解；奇异值增量

1 引言

采用电磁脉冲方式实现油气井下数据传输时，接收信号属于瞬变信号。由于传输距离远，接收到的微弱有用信号往往被环境噪声淹没。因此，有效检测瞬变弱信号是电磁脉冲数据传输的关键技术之一。奇异值分解是一种代数特征提取方法，该技术被广泛应用于数字水印[1,2]、数据压缩[3]、模式识别、图像降噪[4]、故障和缺陷诊断[5,6]以及弱信号提取等领域。奇异值分解的关键是根据需解决的问题和信号特征合理选取主奇异值个数。

本文首先研究了瞬变信号和噪声奇异值的分布特性，提出了相邻奇异值增量概念。然后根据瞬变信号和噪声相邻奇异值增量的不同特征提出一种自适应选择主奇异值个数及自适应奇异值分解方法，并给出该方法检测瞬变信号的具体流程。最后，通过仿真验证了该方法能有效地检测瞬变信号。

2 奇异值分解信号检测原理

2.1 奇异值分解定理

其中

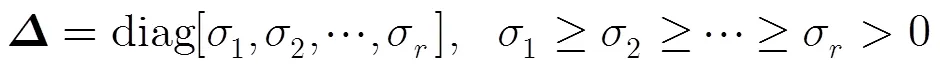
2.2 奇异值分解的信号检测证明

由式(2)得

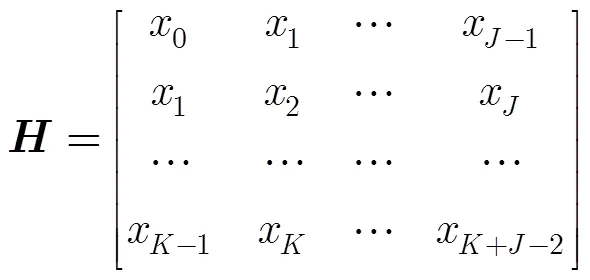
由式(1)可知：

由式(3)可知：

由式(4)得[9]

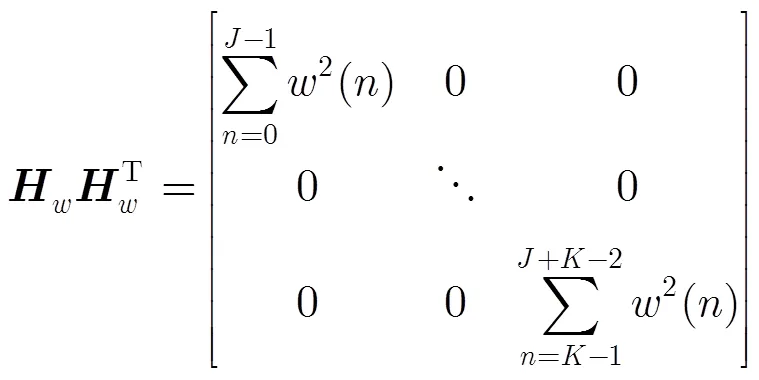
由式(5)，式(6)和式(9)得[10]：

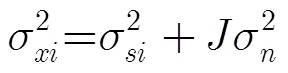
式(10)表明奇异值分解得到的大奇异值与信号相关[11]，因此奇异值分解可以从加噪信号中提取原信号的主要分量，从而实现信号检测。

应用奇异值分解的信号检测中，主奇异值个数的选择非常重要。过大难以有效滤除混在信号中的噪声，过小则滤掉了信号成分。常用方法首先由奇异值定义一个变量，该变量的定义形式有：

(1)定义归一化奇异值[11]：

(2)定义归一化奇异值能量[12]：

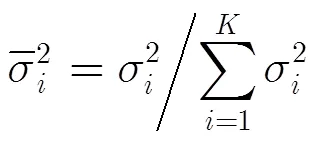
(3)定义奇异值熵[8]：

3 瞬变信号和噪声奇异值分布

3.1 瞬变信号奇异值分布

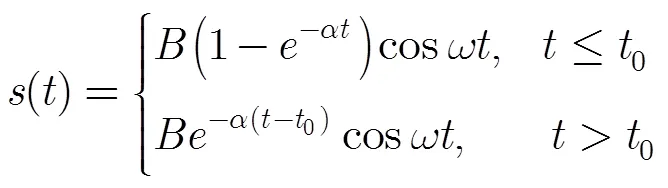
由图1(b)可以看出，前6个奇异值集中了信号的主要成分；进一步研究发现：信号相邻奇异值的差值[8,13]更能反映该瞬变信号的特征，因此定义相邻奇异值增量为

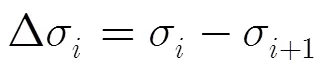
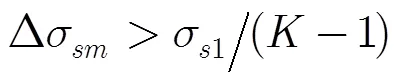
3.2 噪声奇异值分布

井下数据传输时，接收信号中的噪声主要有两大类:井下钻井环境产生的噪声和电子器件产生的电子噪声。在钻井环境中，钻头、井底钻具组合、井内流动的泥浆都是噪声源，这类钻井噪声中主要成分的频率都很低，频率范围为1~4 kHz。电子器件产生的电子噪声是一种高斯白噪声[14]。

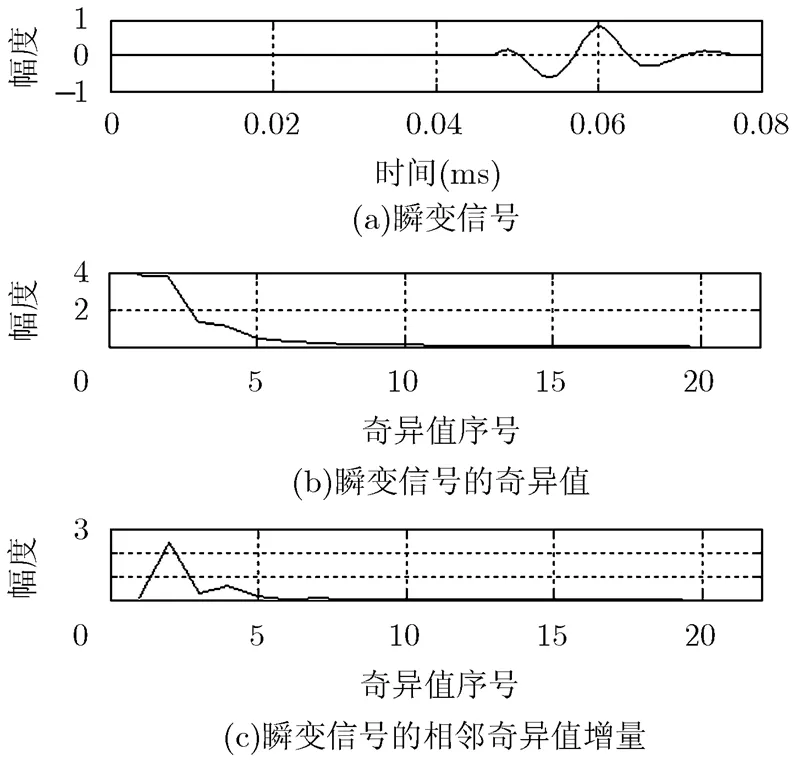
图1 瞬变信号奇异值及其增量

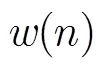
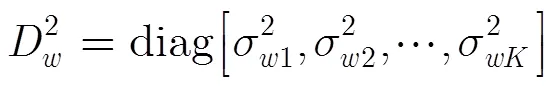
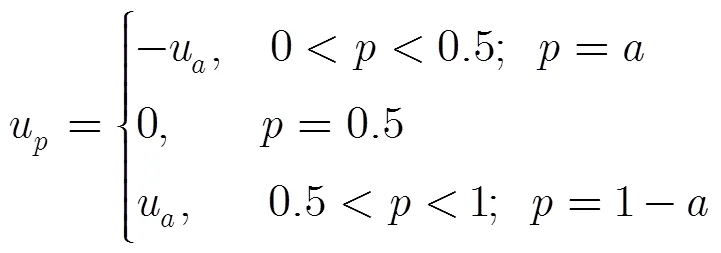
由山内的近似式可知[15]：

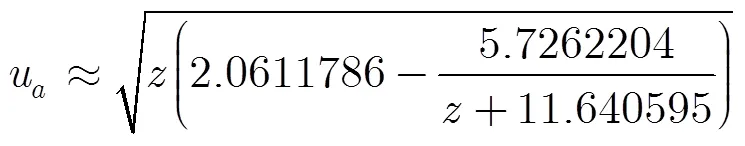
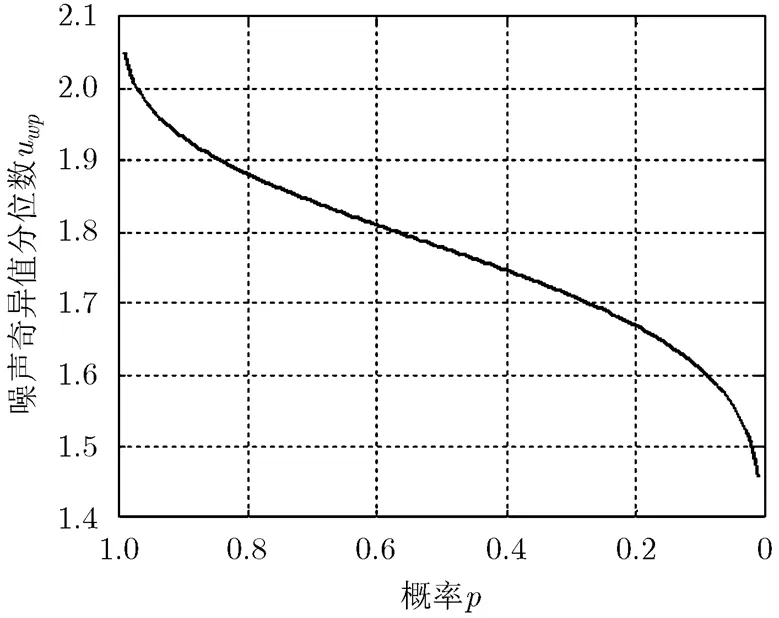
图2 噪声奇异值分位数uwp随p的变化曲线

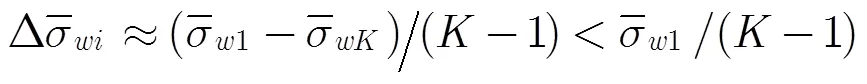
4 自适应奇异值分解瞬变信号检测

由式(16)和式(21)可得，瞬变信号和噪声奇异值和奇异值增量具有如下关系：

图1中；图3中 时的, ,, 。仿真量的计算结果进一步验证了式(22)的正确性。

式(22)表明，瞬变信号的最大奇异值增量与噪声的平均奇异值增量的比值大于瞬变信号和噪声最大奇异值的比值。因此，应用瞬变信号和噪声的相邻奇异值增量的不同，能更好地区分瞬变信号和噪声，可以自适应地确定主奇异值个数，进而去掉噪声奇异值。具体方法是：首先确定瞬变信号最大奇异值增量的幅度和序号，根据幅度和序号确定幅度阈值和序号阈值；然后计算加噪信号的奇异值增量，将序号阈值内的奇异值增量与幅度阈值比较。若有这样的奇异值增量，则其中最大奇异值增量序号作为主奇异值个数，保留主奇异值并将其它置零；若没有，则将所有奇异值都置零。在自适应确定主奇异值个数基础上，得到自适应奇异值分解检测瞬变信号方法，具体流程如图4所示。

图4 自适应奇异值分解检测瞬变信号流程

5 仿真与分析

由图6(a)~图6(d)看出，当被测信号中有瞬变信号时，自适应方法保留的主奇异值个数大约有2个；无瞬变信号时，自适应方法保留的主奇异值个数几乎为零，而采用式(13)~式(15)保留主奇异值个数仍较多。

比较图5(c)~图5(f)可以看出，采用式(13)~式(15)的奇异值分解重建信号虽然都能实现降噪和检测信号，但在没有瞬变信号的时间段，重建信号中仍存在噪声；而奇异值增量自适应奇异值分解方法可以很好地解决上述问题，降噪和检测效果更佳。

图5 -2.5 dB加噪信号的SVD和自适应SVD降噪效果

图6 -2.5 dB下4种SVD方法确定的主奇异值个数

6 结束语

本文通过分析瞬变信号和噪声奇异值特点，提出奇异值增量概念。在研究瞬变信号和噪声的奇异值增量特性基础上提出基于最大奇异值增量自适应确定主奇异值个数的奇异值分解降噪和检测瞬变信号方法。仿真结果表明：针对瞬变信号检测而言，与传统奇异值分解方法相比，利用本文提出的方法降噪后信噪比高，检测效果佳，而且强噪声环境下检测效果更加明显。

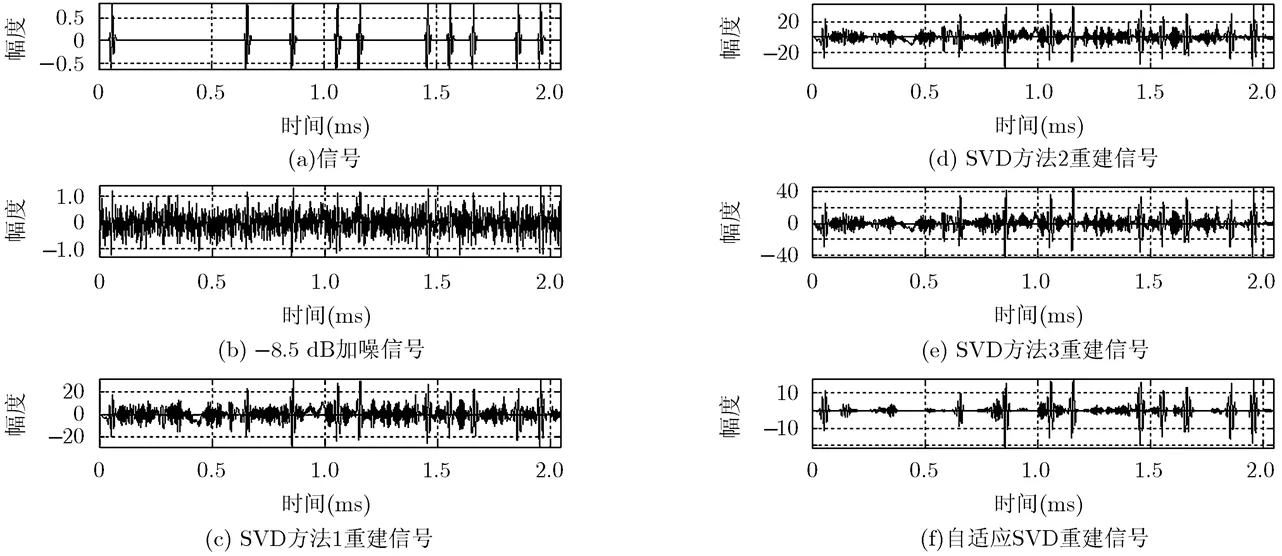
图7 -8.5 dB加噪信号的SVD和自适应SVD降噪效果

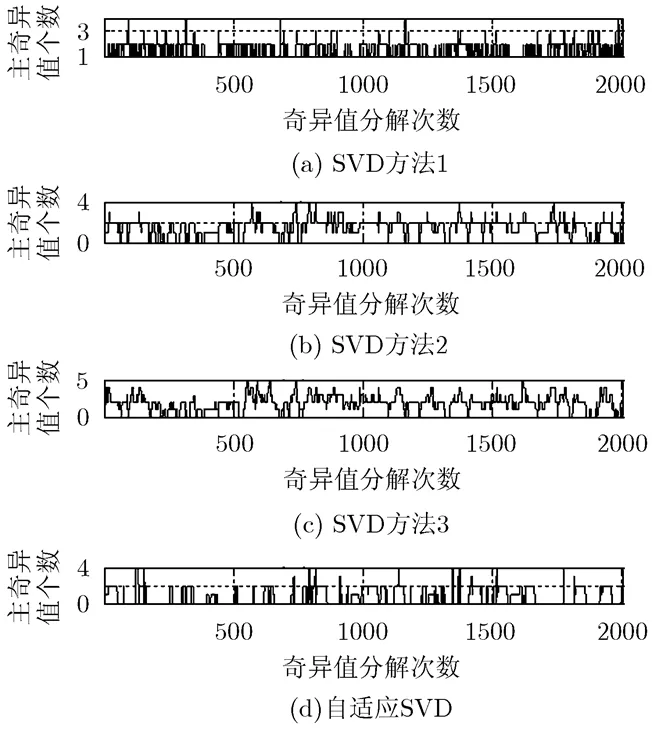
图8 -8.5 dB下4种SVD方法确定的主奇异值个数

[1] Ling Huo-chong, Phan R C W, and Heng Swee-huay. On the security of a hybrid watermarking algorithm based on singular value decomposition and Radon transform[J]., 2011, 65(11): 958-960.

[2] LeiBai-ying, Soon Ing-yann, Zhou Feng,.. A robust audio watermarking scheme based on lifting wavelet transform and singular value decomposition[J]., 2012, 92(9): 1985-2001.

[3] Ahmed S M, Alzoubi Q, and Abozahhad M. A hybrid ECG compression algorithm based on singular value decomposition and discrete wavelet transform[J]., 2007, 31(1): 54-61.

[4] Shih Y T, Chien C S, and Chuang C Y. An adaptive parameterized block-based singular value decomposition for image de-noising and compression[J]., 2012, 218(21): 10370-10385.

[5] Feuillet V, Ibos L, Fois M,.. Defect detection and characterization in composite materials using square pulse thermography coupled with singular value decomposition analysis and thermal quadrupole modeling[J]., 2012, 5: 58-67.

[6] Wang Fei, Xu Fei-yun, and Wang Hai-jun. Local hierarchical non-negative tensor factorization and its application in machinery fault diagnosis[J].( English Edition), 2011, 27(4): 394-399.

[7] Cong Fei-yun, Chen Jin, Dong Guang-ming,.. Short-time matrix series based singular value decomposition for rolling bearing fault diagnosis[J]., 2013, 34(1): 218-230.

[8] Zhao Xue-zhi and Ye Bang-yan. Selection of effective singular values using difference spectrum and its application to fault diagnosis of headstock[J]., 2011, 25(5): 1617-1631.

[9] 周新鹏, 韩峰, 魏国华, 等. 基于噪声子空间奇异值的信号分量数目估计[J]. 电子与信息学报, 2011, 33(9): 2039-2044.

Zhou Xin-peng, Han Feng, Wei Guo-hua,.. Estimation of the number of signal components based on singular values of noise subspace[J].&, 2011, 33(9): 2039-2044.

[10] 刘松, 张水莲, 李世凯, 等. 一种低信噪比损失SVD 滤波部分频带干扰抑制算法[J]. 电路与系统学报, 2013, 18(1): 70-75.

Liu Song, Zhang Shui-lian, Li Shi-kai,.. A low distortion algorithm based singular value decomposition for partial-band interference rejection[J]., 2013, 18(1): 70-75.

[11] 陈希信, 黄银河. 基于矩阵奇异值分解的高频雷达瞬态干扰抑制[J]. 电子与信息学报, 2005, 27(12): 1879-1882.

Chen Xi-xin and Huang Yin-he. A SVD-based approach of suppressing transient interference in high frequency radar[J].&, 2005, 27 (12): 1879-1882.

[12] 汤宝平, 蒋永华, 姚金宝. 基于重分配魏格纳时频谱和SVD的故障诊断[J]. 振动, 测试与诊断, 2012, 32(2): 301-305.

Tang Bao-ping, Jiang Yong-hua, and Yao Jin-bao. Fault diagnosis based on reassigned Wigner-Ville distribution spectrogram and SVD[J].&, 2012, 32(2): 301-305.

[13] 何田, 刘献栋, 陈亚农, 等. 基于奇异值差的转静件碰摩故障诊断方法研究[J]. 航空动力学报, 2009, 24(10): 2296-2301.

He Tian, Liu Xian-dong, Chen Ya-nong,.. Method for diagnosing rub fault of rotor-stator based on differences of singularly values[J]., 2009, 24 (10): 2296-2301.

[14] 肖红兵, 杨锦舟, 鞠晓东, 等. V系统在随钻声波测井数据降噪中的应用[J]. 中国石油大学学报(自然科学版), 2009, 33(2): 58-62.

Xiao Hong-bing, Yang Jin-zhou, Ju Xiao-dong,.. Application of V-system in acoustic logging while drilling data de-noising[J].(), 2009, 33(2): 58-62.

[15] 高惠璇. 统计计算[M]. 第1版, 北京: 北京大学出版社, 1995: 57-60.

徐彦凯： 女，1974年生，讲师，博士生，研究方向为软件无线电及信号处理.

双 凯： 男，1956年生，教授，博士生导师，研究方向为数字信号处理和现代数字处理系统设计.

Detection of Transient Signal Based on Adaptive Singular Value Decomposition

Xu Yan-kai Shuang Kai

(,(),102200,)

This paper introduces the principle of signal detection by Singular Value Decomposition (SVD), and discusses the singular value’s distribution characteristics of the transient signal and Gauss white noise which received from electromagnetic-pulse along the well bore. Then the definition of singular value increment is given, and the signal is distinguished easily from noise according to those singular value increment’s differences. On this basis, an adaptive singular value decomposition method based on selection of main singular value using singular value increment is proposed for the detection of transient signal, and the detailed flowchart of the method is illustrated. Simulation results demonstrate that, the proposed method has a good effect on distinguishing the transient faint signal from noise and the performance outperforms the typical SVD.

Signal detection; Transient signal; Adaptive Singular Value Decomposition (SVD); Singular value increment

TN911.23

A

1009-5896(2014)03-0583-06

10.3724/SP.J.1146.2013.00649

2013-05-09收到，2013-10-22改回

国家自然科学基金(61072074)和中国石油大学(北京)基金(KYJJ2012-05-35)资助课题

徐彦凯 xuyk163@163.com