含风电场的电网可用输电能力研究

蔚曾贞 郭 涛 李 文

（1.国网湖北省电力公司十堰供电公司，湖北 十堰 442011； 2.宁夏电力公司检修公司变电检修中心，银川 750011）

风力发电作为经济、环保的新兴能源，在近期得到了长足的发展。但风能具有波动性、间歇性[1]：当风力发电在电网中所占比重较小时，波动性和间歇性对电网不会带来明显影响；当风力发电装机容量迅猛发展、风电比例不断增加时，波动性和间歇性将会对电力系统的安全、稳定运行以及保证电能质量带来严峻挑战[2]。在电力市场中，可用输电能力（ATC）不仅是电力系统的一个技术指标，反映电网输电容量的市场信号、衡量交易是否可行；也是为调度提供参考，判断系统的安全性，对电网的规划建设起指导作用。因此，研究含风电场的电网可用输电能力是一个符合实际的问题。其对电网安全、稳定、快速运行起指导作用。

1996年美国联邦能源委员会（FERC）颁布了“要求输电网的拥有者计算输电网区域间可用输电能力（Available Transfer Capability，ATC）”的命令，给出了可用输电能力的定义，并规范了可用输电能力的计算。它给出的可用输电能力的定义为：在现有的输电合同基础上，实际物理输电网络中剩余的、可用于商业使用的传输容量，用公式可表示为

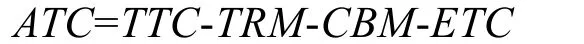
式中，TTC为最大输电能力；TRM为输电可靠性裕度；CBM：容量效益裕度；ETC为现存输电协议。

1 异步发电机稳态PQ 模型

目前，我国风力发电机组主要有两种：异步风力发电机和双馈风力发电机。其中异步风力发电机占大多数。本文研究当风电发电量占整个电网不同比重时，电网ATC 的变化与风力发电量、风电网并入节点电压的关系。

由于异步风力发电机对系统来说，发出有功功率，吸收无功功率。因此，考虑风电场对电网ATC 的影响，必须要考虑风电场在电网中吸收的无功功率。本文对单台异步风力发电机组采取稳态PQ 模型，根据风电场发出的有功功率计算风电场在电网中吸收的无功功率。如果忽略机械损耗、附加损耗和铁耗，异步电动机的稳态等值电路如如图1所示。

图1 异步发电机稳态等值电路

由图1可以看出，异步电动机输出的有功功率为Pe，即为注入电网的功率表达式为：

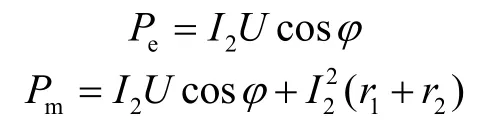
令r=r1+r2、x=x1+x2，则

两边平方：

展开后得：

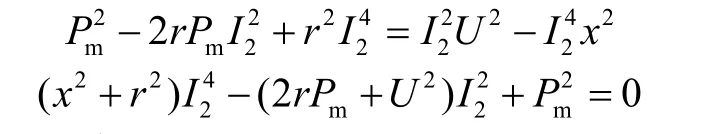
解方程得：

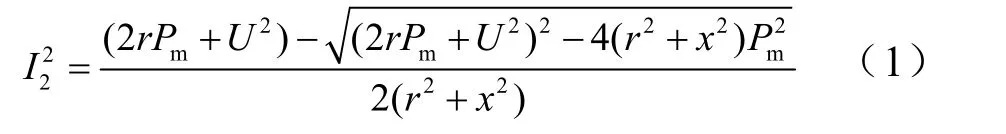
根据预测风功率，可以很快计算出风力机从风能中实际得到的有功功率Pm。根据图1异步发电机稳态等值电路，我们可以得到PQ如下关系式：

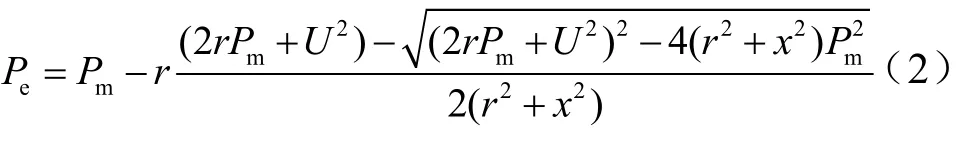
若忽略定子、转子电阻铜耗和漏抗无功损耗，则：

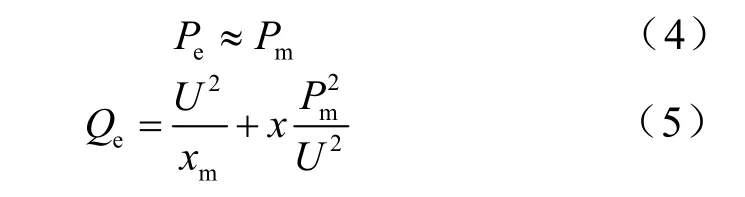
由式（4）至式（5）可以看出，异步风力发电机吸收的无功，不仅与风力发电机发出的有功功率有关，还与风电场并入电网节点的节点电压U有很大关系。根据异步发电机参数和预测的风功率曲线，在风电场并网节点电压U恒定为风力发电机额定电压的情况下，我们初步描绘出风电场单台风力发电机组24h 内PQ 变化曲线（图2）。

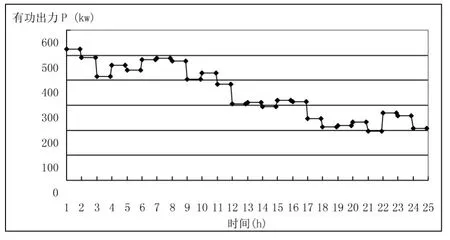
图2 PQ 变化曲线图

2 含风电场的电网ATC 计算

区域间电网的可用输电能力的定义为：在保证系统稳定的情况下，通过2 区域间的所有输电回路，从一个区域/点向另一区域/点可能输送的最大功率[3]。本文以ΙEEE-14 节点系统为例，研究含风电场的电网静态ATC。

2.1 目标函数

根据区域间可用输电能力的定义，将系统分为两区域：送电区域（G 区域）和受电区域（L区域）。节点12、13、14 在受电区域，其余在送电区域；发电机1、2、3、6、8 均在送电区域；各交流支路的传输极限为1500MW；风电场通过变压器和母线接入系统的2 号节点。建立该系统G 区域往L 区域送电的可用输电能力的目标函数，目标函数可表示为

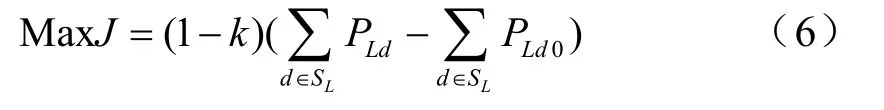
其中，SL为选定区域的负荷集合；PLd为母线d上的负荷；PLd0为现存输电协议；k为裕度系数，是保证系统安全稳定运行留出的CBM，这里取10%～15%。

2.2 用内点法列出等式不等式约束

设定ΙEEE14 节点系统节点1 为平衡节点，节点1、3、6、8 为PV 节点，其余为PQ 节点，系统的基准容量取100MW。G 区域、L 区域中各交流支路的传输极限均为1500MW；各发电机的有功出力和无功出力范围分别为：0～2000MW，-500Mvar～1000Mvar。考虑网络拓扑结构约束、线路热稳定约束、暂态稳定约束、节点电压约束、动态稳定约束、发电机有功无功出力约束等，可列出如下等式约束：

其中，SG为选定送端区域的所有发电机节点集合；SL为选定受端区域的所有负荷节点集合；SS为装有无功补偿装置的节点集合；SN为系统所有节点集合；SNL为系统所有支路集合；*表示基态潮流中的值。

2.3 计算流程

计算含电场的电网ATC 必须要考虑到风电场并入电网节点电压的变化。在采用内点法求解电网的ATC 时，每次迭代风电场并入电网节点电压都发生了改变，因此，每次迭代代入的PQ 值都将不同。具体步骤为

1）在给定风速的前提下，根据公式（1）确定异步电动机输出的有功功率Pe。

2）确定风电场并入电网发出的有功、吸收的无功数值。根据式（4）和式（5），通过编程计算出风力发电机无功功率Qe。由于本文考虑大型风电场并网的情况，因此，该风电场输出的有功功率为nPe，吸收的无功功率为nQe。n为该风电场含异步电动机的台数。

3）将风电场并网节点视为PQ节点，将风电场输出有功nPe、吸收无功nQe看作节点功率注入电网中，考虑网络约束条件计算此时电网的实际可用输电能力。

4）由于nPenQe的注入造成电网电压波动，从而使得Qe发生改变。因此需要多次迭代，保证风电场并网节点电压恒定。在节点电压恒定的基础上，求出的最大电网可用输电能力才有研究意义。整个流程如图4所示。

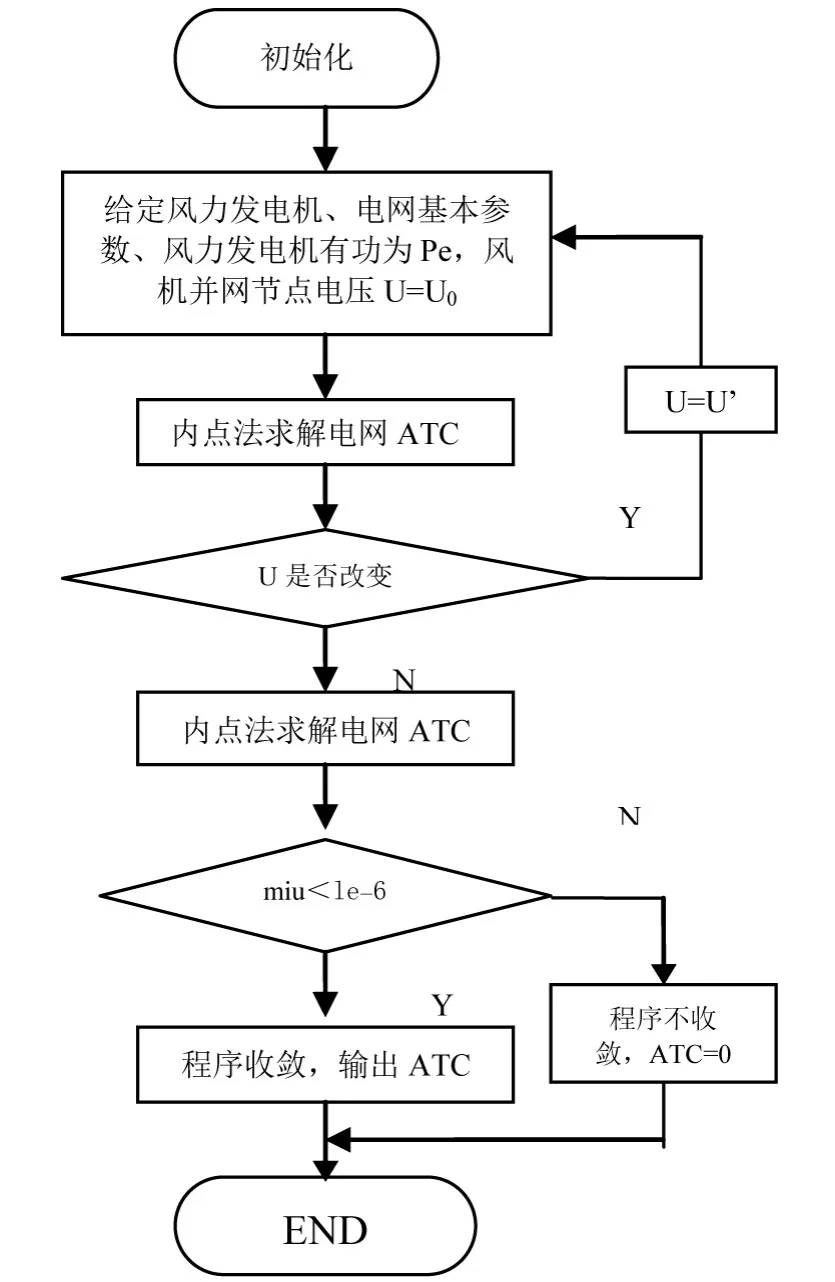
图4 计算流程图

2.4 计算结果

通过上述模型，已知风电场出力，我们可以求解出对应的电网可用输电能力。已知风电场单台风力发电机组24h 内PQ 变化曲线（图2），我们可以通过改变异步电动机的数量来改变风电场的出力，分析风电场出力的大小对电网可用输电能力的影响。

当风电场含20 台异步风力发电机组时，通过Matlab7.1 编程，求出不同时刻G 区域往L 区域送电的最大可用输电能力（ATC）数值，并绘制出节点2 的电压波动曲线和区域间电网最大可用输电能力波动曲线，如图5、图6所示。同理可求出当风电场含150 台异步风力发电机组时，不同时刻G 区域往L 区域送电的最大可用输电能力（ATC）数值，并绘制出节点2 的电压波动曲线和区域间电网最大可用输电能力波动曲线，如图7、图8所示。其中，节点2 的电压波动曲线是以并网前节点2 的电压为基准绘制出来的。

图5 节点2 的电压变化曲线

图6 G 区域往L 区域送电的ATC 变化曲线

图7 节点2 的电压变化曲线

图8 G 区域往L 区域送电的ATC 变化曲线

3 结论

对比当风电场所含异步风力发电机组台数不同时，即风电场出力占电网比例不同时，区域间电网最大可用输电能力波动曲线（图5、图7）的变化趋势与节点2 的电压波动曲线（图6、图8）的关系，得出：

1）当风电场占电网比重较小时，电压波动不是影响电网可用输电能力（ATC）变化的主要因素，可用输电能力的变化主要与风电场发出的有功功率有关：电网的可用输电能力随着风电场发出的有功功率增加而降低，与风电场发出的有功功率呈反比趋势。

2）当风电场占电网比重较大时，风电场并网节点电压不稳定，电网需要从外部吸收大量的有功、无功维持系统状态稳定，此时，电网的可用输电能力与风电场发出的有功功率没有明显关系，与风电场并网节点电压有关。

[1] Transmission transfer capability task force.Available transfer capability definitions and determination[Z].North American Electric Reliability Council,Princeton,New Jersey,1996.

[2] 李庚银,高亚静,周明.可用输电能力评估的序贯蒙特卡罗仿真法[J].中国电机工程学报,2008,28(25): 74-79.

[3] 郭永基.可靠性工程原理[M].北京:清华大学出版社,施普林格出版社,2002.