两种PWM控制算法的比较研究

肖立志，廖萍，邱大强

(1.国网四川省电力公司检修公司，四川 成都 610000;2.国网四川省电力公司，四川 成都61000)

1 引言

PWM换流技术作为电能变换的核心技术之一，该技术广泛应用于风电和分布式电源等可再生能源并网和满足工业技术要求、节约能源为目的电源变换［1］。为了更好的实现高效、大功率的电能变换，大多数学者分别从换流系统主电路结构和换流控制算法两个方面对其进行深入的研究。当前换流元件受耐压、绝缘和散热等限制而无法做到较高电压和大电流，许多高电压、大容量换流器均采用多个换流元件的串联和并联来实现的，因此而对于这些多个换流元件的控制研究就显得尤为重要。目前用于换流控制的算法较多，其控制原理和方法各不相同、控制效果差别较大，因此，如何选择最佳的控制算法来满足自身系统的换流控制已经显得尤为重要。

目前研究PWM换流系统的控制算法主要可以分为两类:一类是基于电压幅值和相位的间接电流控制，它根据电源输入的电压幅值和相位与换流系统输出的基波电压的关系来控制有功功率的传输，而无功功率需采取附加措施来调节，该控制算法不能实现有功和无功的独立控制，具有交流侧电流动态响应慢、对系统参数变化灵敏等缺点［2－5］。另一类是基于同步旋转坐标系下的直接电流控制，其普遍采用内环电流反馈和外环电压前馈的解耦控制，这种控制器采用PI调节方式实现，然而控制器的电路参数对PI参数设计影响较大，而 PI参数准确度对决定了控制器的响应［6－10］。目前有学者提出从功率控制的角度出发来完成换流系统的控制，这种算法采用功率外环、电流内环的方法，并且只使用一个PI控制器，简化了换流控制系统的结构，参数选择也更加容易。

针对换流控制算法选择的复杂性，本文主要研究了双闭环直接电流控制和直接功率控制的基本原理与结构，并通过仿真比较了两种控制算法的各项性能指标，为换流控制系统设计提供重要的参考。

2 PWM换流系统模型

电压型PWM换流器是由可关断器件(如:IGBT、IGCT)、换流电抗器、直流电容器等器件组成，其主电路结构如图1所示，其中换流电抗器是电源与换流系统之间功率传输的纽带，并起到抑制换流器输出电压、电流中高次谐波的作用。直流电容为负载提供电压支撑，并具有抑制直流电压波动的作用。

图1 电压型换流器电路图

图1中，uj和ij(j=a、b、c)分别为电源的电压和电流;L为换流电抗器，C为直流电容，RL为负载。假设电源三相平衡，根据换流系统结构可得三相静止坐标系下的数学模型［11］:

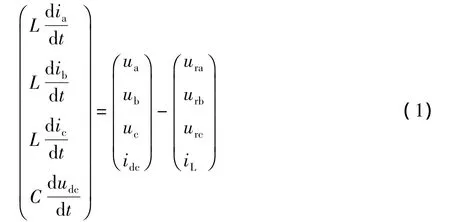
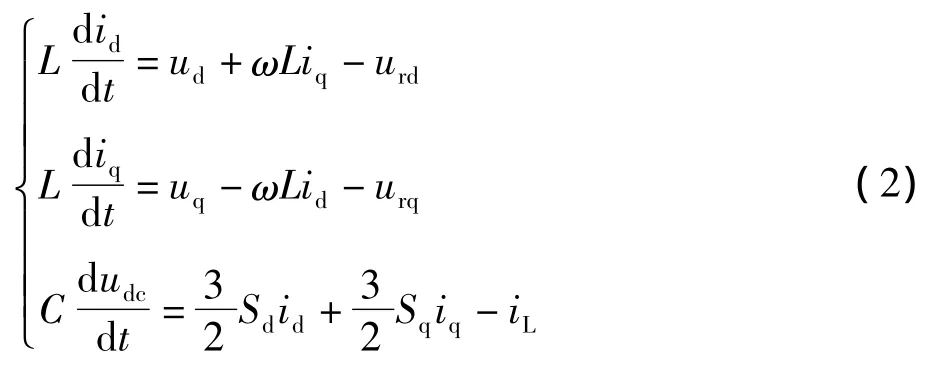
式中:Sd=urd=Sdudc;urq=Squdc。通过式(2)可以看出，通过dq变换就能将的稳态正弦电流变成了直流量，然后在通过PI调节器的直流增益为无穷大，就可以实现电流的无差跟踪控制。

3 两种控制算法原理比较

3.1 双闭环直接电流控制

双闭环直接电流控制算法的原理是电压外环根据直流电压udc的实时测量值与u*dc期望值进行比较，然后将其差值信号转化为内环的电流参考信号，再将该电流引入内环并采用前馈解耦的方式消除dq轴电流的耦合关系。电流内环的引入使得系统的动态调整性能较好，电流跟踪速度较快，实现单位功率因数或者功率因数可变。

由式(2)可知，三相PWM换流系统在两相同步旋转坐标系中，其dq模型可描述为:

式中 ud，uq是电源的 d、q 分量;urd，urq换流系统交流侧电压d、q分量;id，iq换流系统交流侧电流d、q分量;s为微分算子。从式(4)可以看出，有功电流和无功电流相互耦合，任何一轴方向上电流的变化都会引起另外一轴方向电流的变化。所以一般的PI调节很难达到理想的控制效果，为此将检测到的实际电流补偿两相电流间的祸合，从而消除电流之间的相互影响，实现电流的解耦控制则urd，urq的控制算法为:

式(5)中Kip，KiI为电流调节器的P、I参数。有功电流指令值i*d与负载电流成正比，其值为电压调节器的输出:

式(6)中，Kvq，KvI为电压调节器的 P、I参数。根据以上分析就可以得到PWM换流系统双闭环直接电流算法的控制结构图，如图2所示。

3.2 直接功率控制

根据瞬时无功功率理论可得，换流系统有功功率与无功功率可分表示为:

图2 双闭环直接电流控制结构图

根据式(1)的第四式可得，将等式两边同乘以ucd经等效变换后即可得:

由d、q坐标下瞬时复功率的定义为:

取电源a相的矢量方向作为d轴，q轴超前其90°。设电源为理想电源，则有uq=0可得:其中ψ*

dq为电感磁链。由此可见，通过控制电感磁链的各分量即可控制有功功率和无功功率的增量。由式(10)可得:

对式(11)在一个采样周期内进行积分，由于采样频率 f较高，在一个采样周期内 ud，uq，urd，urq保持不变，得

其中，Tk为K时刻采样，从而有

最后在通过在将其变换三相静止坐标系下控制开关器件导通即可实现控制［13］。

通过上文对两种控制原理的分析可以看出，两种方法的电压外环都是通过实际采样值与期望值相减后经过PI控制器分别转换为内环参考电流或内环参考功率;双闭环直接电流再通过将实际的输入电流追踪参考电流从而实现电压的控制，而直接功率则是调整输入功率从而实现系统控制。通过比较图2和图3可以看到，双闭环直接电流采用了3个PI控制器，直接功率控制则仅采用了一个PI控制器，由于PI控制器对系统参数较为敏感，因此在系统参数改变时双闭环直接电流控制系统参数调试比较麻烦。

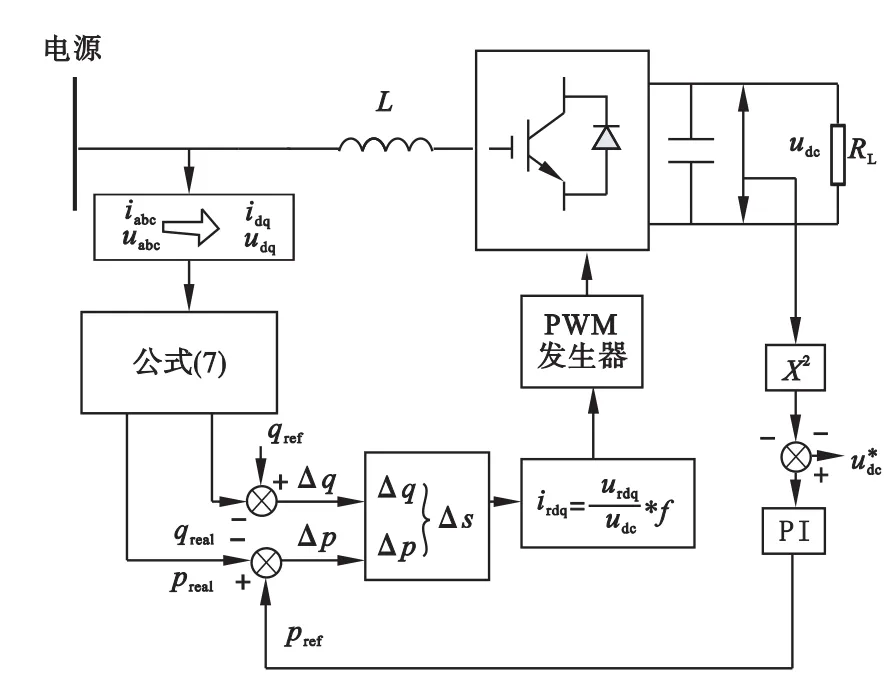
图3 直接功率控制结构图

4 两种控制算法仿真结果比较

为了比较两种控制算法的实际控制效果，本文利用Matlab软件分别对其进行了多次仿真，系统仿真的结构如图1所示，其主要参数如表1所示。

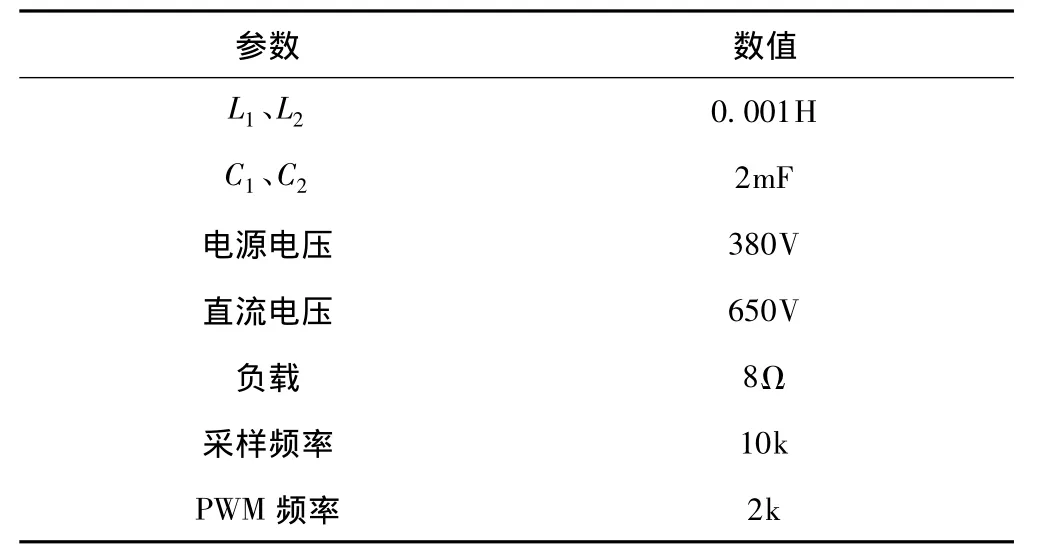
表1 换流系统参数

换流控制系统的控制性能的比较主要是从控制系统在换流系统启动过程中的上升速度、超调量和负载突变时的抗扰动控制来评估其控制效果，图4和图5分别是利用两种控制算法控制所得到的仿真结果。

图4 双闭环直接电流控制仿真结果

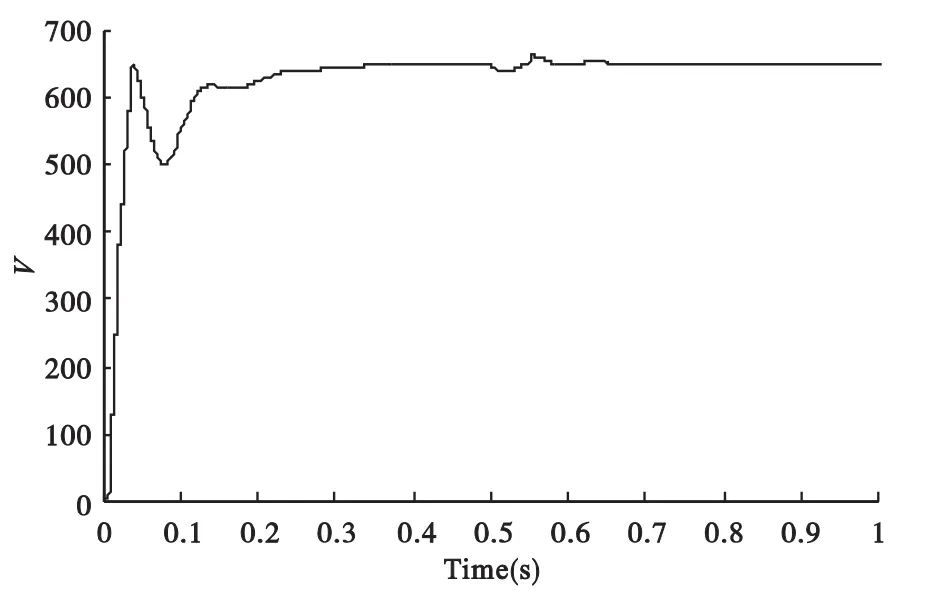
图5 直接功率控制仿真结果

通过对比图4和图5可知，在换流系统最开始建立直流电压的过程中，两种控制算法的稳态所需要的建立时间基本相同，均为0.2s左右，但是双闭环直接电流控制的超调量比直接功率控制要大很多。同时，当系统在0.5s时负载突变，双闭环直接电流控制的直流电压有一个明显的下跌和恢复过程，直接功率控制算法对于这个扰动的抗干扰性则明显优于双闭环直接电流控制算法。

5 结论

本文首先简单介绍了PWM换流系统的基本数学模型，在此基础之上详细的分析了双闭环直接电流控制和直接功率控制的基本原理和控制系统结构，并利用对这两种控制算法设计了各自相应的控制器，最后利用Matlab软件对这两个控制算法进行了仿真。文章通过从原理分析和仿真得出以下结论:

(1)双闭环直接电流控制算法设计的换流系统控制器总共需要三个PI调节器而直接功率控制算法说设计的控制器仅需要一个PI调节器，由于PI调节器对系统参数较为敏感，因此，采用直接功率控制算法设计控制器相对比较容易。

(2)通过Matlab软件对换流系统进行了模拟仿真，仿真结果表明直接功率控制在系统启动过程中的超调控制和抗扰动能力明显优于双闭环直接电流控制。

［1］张崇巍，张兴.PWM整流器及其控制［M］.机械工业出版社，2003.

［2］张勉华.三相PWM整流器研究［J］.电工技术学报，1996，11(4):27－30.

［3］伍小杰，罗悦华，乔树通.三相电压型PWM整流器控制技术综述［J］.电工技术学报，2005，20(12):7－11.

［4］王英，张纯江，陈辉明.三相PWM整流器新型相位幅值控制数学模型及其控制策略［J］.中国电机工程学报，2003，23(11):85－86.

［5］朱俊杰，周凯.双闭环PWM整流器的SIMULINK建模与仿真［J］.电气传动自动化，2005，27(3):26－27.

［6］陈伟，邹旭东，唐健，等.三相电压型PWM整流器直接功率控制调制机制［J］.中国电机工程学报，2010，30(3):35－37.

［7］王久和，李华德，李正熙.电压型PWM整流器直接功率控制技术［J］.电工电能新技术，2004，23(3):64－65.

［8］王久和，张金龙，李华德.电压型PWM整流器直接功率控制系统主电路参数设计［J］.北京科技大学学报，2006，28(11):1092－1094.

［9］王久和，著.电压型PWM整流器的非线性控制［M］，机械工业出版社，2008.9.

［10］Ibrahim Kaya.IMC based automatic tuning method for PID controllers in a Smith predictor configuration.Computers ＆ Chemical Engineering［J］，2004，28(3):281－290.

［11］Dawei Zhi，Lie Xu，Williams B.W.Improved Direct Power Control of Grid-Connected DC/AC Converters［J］，IEEE Transactions on Power Electronics，2009，24(5):1280－1292.

［12］Bouafia A.，Krim F.Gaubert P.Fuzzy-Logic-Based Switching State Selection for Direct Power Control of Three-Phase PWM Rectifier［J］.IEEE Transactions on Industrial Electronics，2009，56(6):1984－1992.

［13］邱大强，李群湛，马庆安.基于直接功率控制的柔性高压直流输电系统控制策略研究［J］，高电压技术，2010，36(10):2600－260.