有限数量PMU优化配置算法及其潮流误差分析

李延平，贾志军，白丽燕

(兰州供电公司，甘肃 兰州 730050)

1 引言

基于GPS的相量测量单元(PMU)在广域测量系统中得到应用以后，由于其对节点电压、支路电流相量的高精度直接测量，使其在电力系统中的发展得到关注，同时PMU的最优配置问题也成为了重要研究课题。

PMU的最优配置问题分为两类:一是以特定应用需求为目标的配置方法，二是以电力网完全可观测为目标的配置方法。特定应用需求主要有提高状态估计精度、电压稳定性分析及线路故障定位等，这类方法主要依据PMU测量的优势，修正状态估计模型，对SCADA系统数据进行可靠的补充。但这些目标的应用繁多配置方法的可移植性差，从而阻碍了它的应用。后者则以完全可观测为目标，可移植性较好，理论上具有优势。因此本文研究重点在于以配置最少数量PMU保证系统结构完全可观测的PMU最优配置问题，寻找一些优化算法来实现该优化配置问题。

2 电力系统可观性定义

从量测角度来看，电力系统可观测是指系统的量测集合(数量和种类)及其分布足够求解当前状态。而传统的能量管理系统(energy management system，EMS)的数据时稳态或者是准稳态数据，因而只能监视电网的静态特征，而无法对电网的动态过程进行分析，也不能对潜在的动态行为进行预测。PMU设备采集的数据能从时间、空间和幅值3维坐标角度实时观测电网全局的动态过程，因此可用来描述系统的整体可观性。系统可观性可从“代数可观”与“拓扑可观”两种角度考察。

2.1 代数可观性原理

假设一个电力节点系统由n个节点、m个测量值，即可得式(1):

其中，Z为m维的列向量，并代表m个测量量;X为n维列向量，代表n个节点的待测量;V为测量过程中所产生的m维的噪声矩阵;H矩阵为对应的m×n雅克比矩阵。若H为满秩矩阵，即rank(H)=n，则该系统是代数可观的。

若H、z采用实数矩阵，则定义变为:一个有n个节点，m个测量量的电力系统可用方程Z=HX+V，描述，其中Z为m维测量向量;H为m×(2n－1)维测量量雅可比矩阵;X为2n维电压状态矢量;V为m维测量噪声向量。若H为满秩的，即rank(H)=2n－1，则这个系统是代数可观的。

2.2 拓扑可观性原理

在图论的角度上可以将电力系统视为是由n个顶点、m条边构成的图:

其中V表示图的顶点集合，E表示图的边集合，它们分别对应于系统的母线与支路集合。测量网络构成了一个测量子图 G'=(E'，V')，并且 V'⊆V，E'⊆E。若满足V⊆V'，E⊆E'，即若子图G’包含图G的所有顶点和支路，则系统是拓扑可观的。

3 PMU优化配置算法

3.1 改进的深度优先搜索算法

深度优先搜索算法(DFS)是基于图论的一种配置PMU的搜索算法，它优先选择连接支路数最多的节点安装PMU，如果具有连接支路数相同的情况，则随机选取其中1个用于安装PMU。所有PMU都根据这一相同法则来确定安装位置，直到整个电网达到可观性要求。

在考虑了节点的重要度和直接测量、间接测量等因素后，对原有的深度优先搜索算法稍加改进，得到本章所介绍的深度优先搜索算法来进行PMU配置。

原有的深度优先搜索算法，在配置PMU时并没有考虑到发电机母线和负荷母线的重要性、PMU节点覆盖面的大小和PMU配置后对后续PMU节点的选择的影响等因素。在对深度优先搜索算法进行改进的时候，进一步考虑如下因素:(1)发电机母线和负荷母线的重要程度;(2)PMU节点覆盖面的大小;(3)PMU节点对后续节点选择的影响。

3.2 与二分法配合的模拟退火算法

将模拟退火算法应用于PMU优化配置问题中，需要考虑到电力系统的特点，明确模拟退火算法的各个参数的含义、控制参数的设置以及目标函数的确定。

由于模拟退火算法收敛速度较慢，为了尽量减少运算量，将二分法与模拟退火算法进行配合，先用二分法确定PMU节点的数目，再对该数目的PMU节点应用模拟退火算法确定最优配置方案。模拟退火算法中各参数的选择直接影响到算法收敛速度和运行时间。参考文献中模拟退火算法中参数意义的解释和研究，下面对各参数的选择作出说明。

(1)初始温度的选取

初始温度是影响模拟退火算法全局搜索的重要因素之一。初始温度越高，算法搜索到最优解的可能性越大，花费的时间也越长;初始温度越低，虽能节约计算时间，但影响全局搜索性能。通过几次的试验性运行，对于不同规模的电力系统，初始温度应选择不同的值，选择初始温度为T0=3×n，n为电力系统的节点数目。

(2)温度下降函数的确定

将温度下降函数选为tk=βtk－1，即每次降温后的温度为降温前温度的β倍，β取0到1中的一个数。这种降温函数的优点在于:高温区温度下降较快，低温区温度下降较慢，这样可以将寻优的重点放在低温区，有利于PMU的优化配置。

(3)马尔科夫链Lk长度选择

将马尔科夫链的长度选为固定值，也就是在不同温度下，马尔科夫链是相同的。但是与初始温度选择类似，不同规模的电力系统马尔科夫链的长度是不同的，当电力系统有n个节点时，Lk=3n。

(4)终止温度的选择

为能尽量找到最优解，达到应有的效果，将终止温度选为0.1。

中模拟退火算法中退火函数的设计和步骤设置原理，并结合二分法的原理设计如下算法流程。

与二分法结合的模拟退火算法步骤如下:

第一步:计算节点系统的平均度，以确定最初的PMU配置数目n1，并以n1为配置数目的上限，n2=0为配置数目的下限;

第二步:对n1个PMU应用模拟退火程序，找出最优配置方案;

第三步:采用二分法确定需要配置PMU的个数nx=(n1+n2)/2(nx取整数);

第四步:调用模拟退火程序，找出配置方案;

第五步:调用系统可观性分析程序，分析在nx个PMU的配置方案下，系统是否完全可观;若可观则将nx赋给n1，并执行第三步;若系统不可观，则执行第六步;第六步:判断n1与 nx的关系，若n1比 nx大1，则说明n1个PMU是该系统配置PMU的最小数目了，结束算法，PMU的数目即为n1，方案为n1个PMU时的方案;否则，将nx赋给n2，再执行第三步。

算法流程图如图1所示。

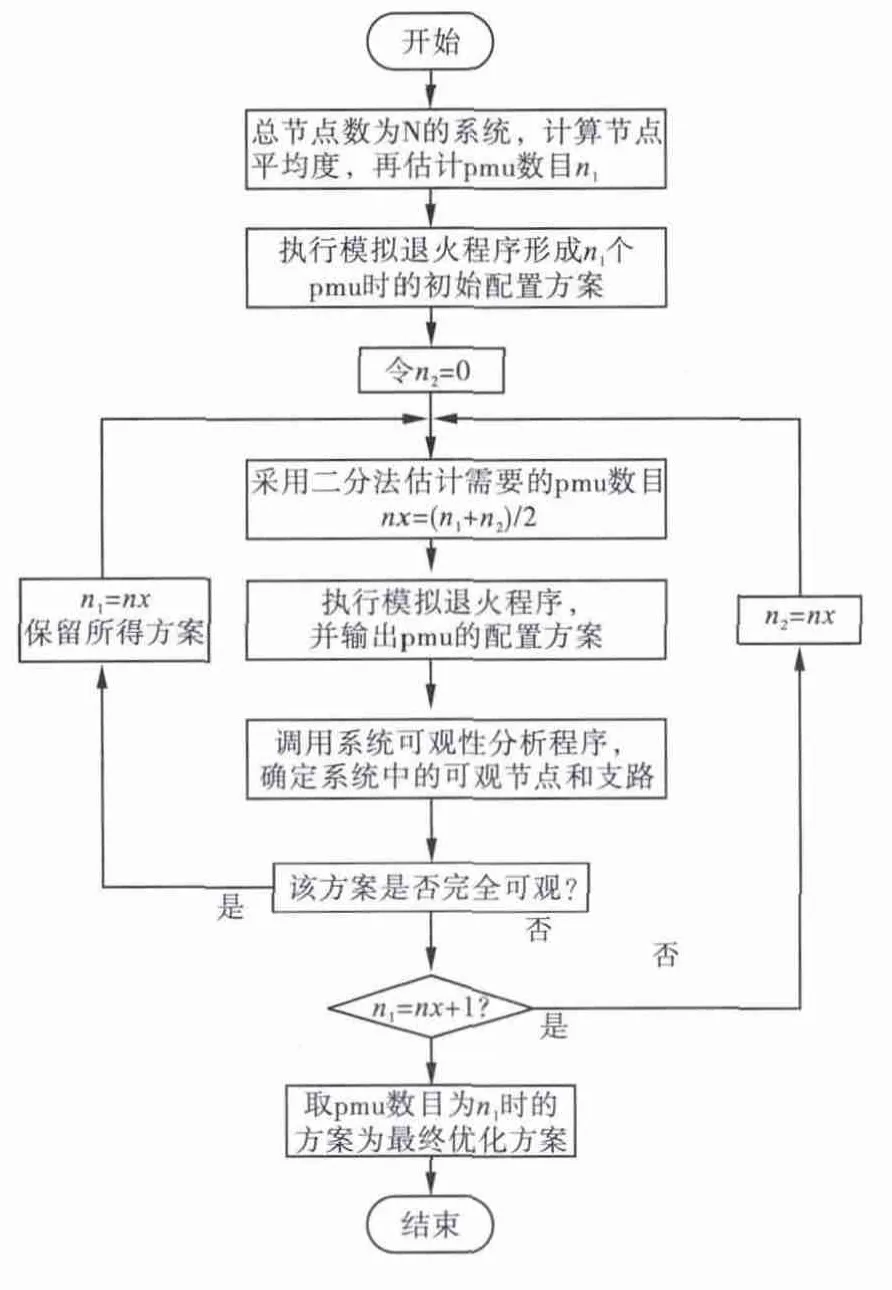
图1 模拟退火算法流程图

4 仿真算例与结果对比

在PMU配置问题中，衡量最终优化方案优劣的指标有多个，本文中以最终配置PMU数目和冗余度大小作为衡量其优劣的指标。最终的PMU数目越少，说明该方案经济性越好，这个是判断方案优劣的第一指标。而冗余度大小的比较是以PMU数目相同为前提的，冗余度越大说明测量的可靠性会越好。

对于有零注入节点的系统而言，其冗余度如式:

式中:集合 P为配置了PMU节点的集合;d为PMU节点邻接的节点数;k为零功率注入点的数目;n为该系统节点的总数。

对比各个节点系统下，两种不同算法得出的配置方案，其结果如表1所示。

由于模拟退火算法得出的配置方案有多个，上表中所列的模拟退火算法的方案只是配置PMU数目相同时冗余度最大的配置方案。

5 基于PMU配置的潮流推算误差

为验证第三章中深度优先搜索算法和模拟退火算法得出的最终配置方案的可行性，本文采用IEEE 39节点系统对以上两种方案进行仿真验证，并与PSASP仿真分析得到的潮流进行误差对比。

IEEE 39节点系统如图所示，选取31号节点作为平衡节点。系统基准容量为100MVA，系统的基准电压为345kV。

图2 IEEE 39节点系统

根据3、4节得到的优化配置方案采用不同的PMU配置方法，经推算后得到全网的节点电压相量和各支路首末端功率。推算结果与PSASP中潮流计算结果比较，其误差曲线如图3～图6曲线所示。

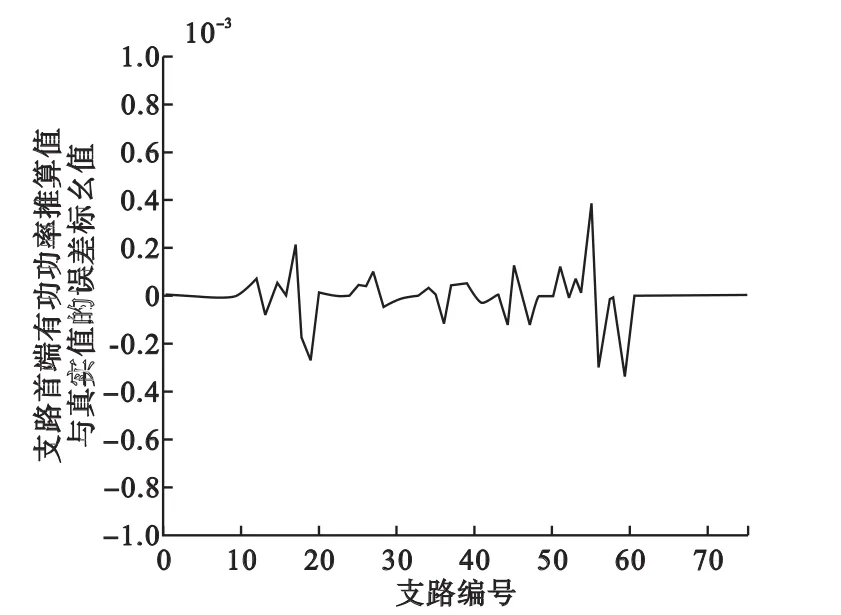
图3 DFS算法的节点电压推算误差曲线

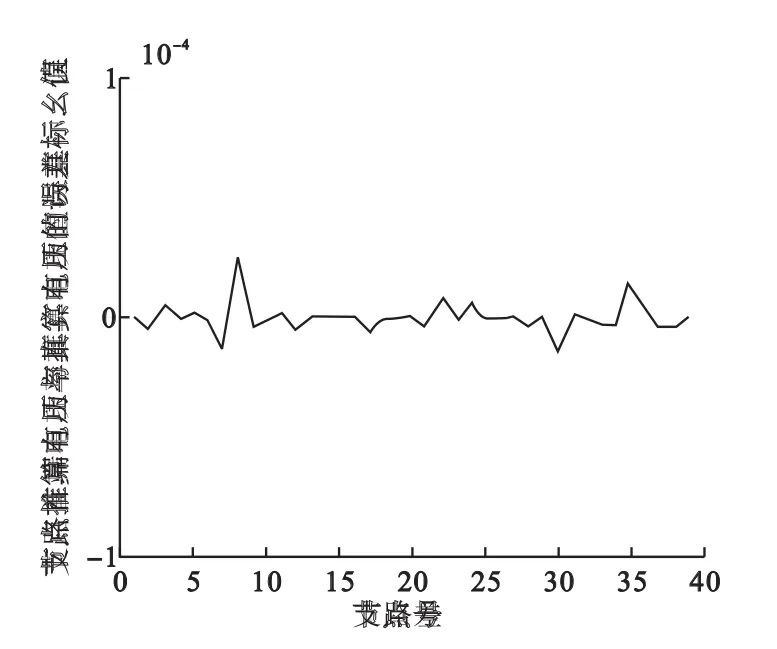
图4 SA算法的节点电压推算误差曲线

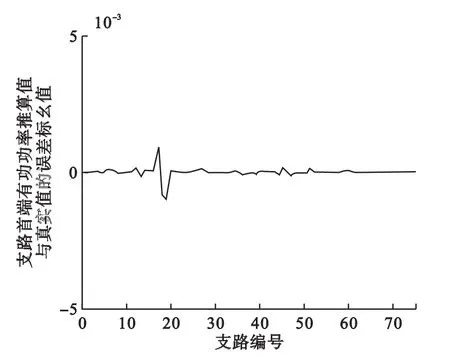
图5 DFS算法的支路首端有功功率推算误差曲线

通过图3～图6的对比可知:由深度优先搜索算法以及与二分法配合的模拟退火算法的配置方案推算得到的节点电压和支路潮流与PSASP软件得到的结果进行误差分析，可以看出:推算出的IEEE39节点系统的节点电压值误差很小，推算结果与真实结果差值不超过标幺值的万分之一;支路首末端的有功功率推算误差的标幺值在千分之一以内;而支路首末端无功功率推算误差的标幺值在千分之二以内。可见，推算结果的误差很小，在可接受范围之内。

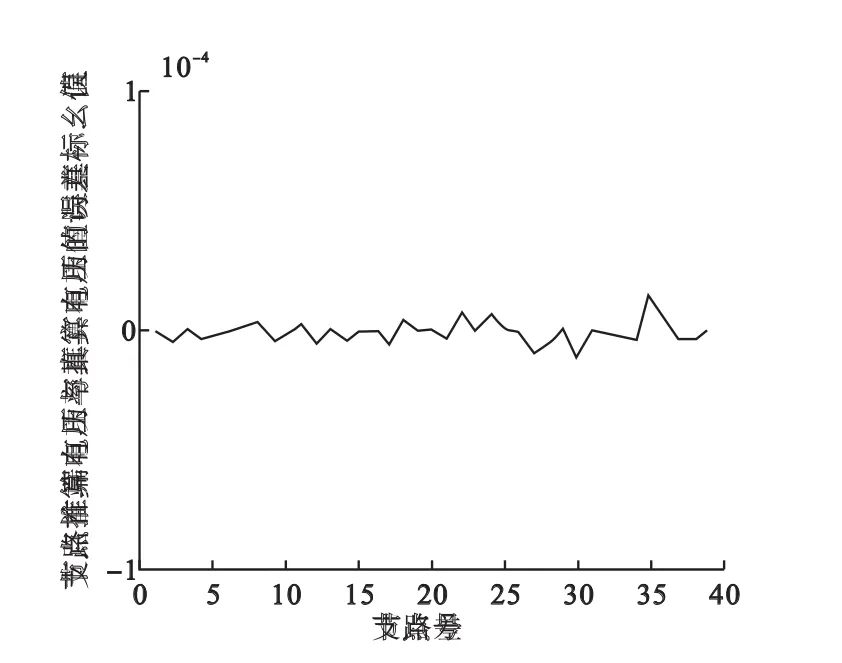
图6 SA算法的支路首端有功功率推算误差曲线

6 小结

本文对深度优先搜索算法和模拟退火算法得出的最优配置方案，应用推算原理，以PMU节点的电压和潮流数值作为原始数据，对全网各节点的电压和支路的潮流进行推算，分析推算结果数据与系统数据真实值之间的误差，得到良好效果，电压误差能控制在万分之一以内，有功潮流误差在千分之三以内，无功潮流误差在百分之三以内，基本满足电力系统的可观性要求。

但是，在PMU优化配置问题研究方面只考虑到了电力系统的静态特性，推算原理皆基于电力系统的稳态数据，故稳态情况下该配置方案的可行性。至于在电力系统受扰情况下，PMU优化配置算法是否仍旧可行，其配置方案能否满足全局可观的要求仍需继续研究。对于特殊情况要求下，PMU优化配置算法又当如何改进仍然需要解决。

参考文献

［1］Abbasy Nabil H，Ismail Hanafy Mahmoud，A unified approach for the optimal PMU location for power system state estimation［J］.IEEE Trans on Power Systems，2009，24(2):806 －813.

［2］Aminifar Farrokh，Lucas Caro，Khodaci Amin，etal.Optimal placement of phasor measurement units using immunity genetic algorithm［J］.IEEE Trans on Power Delivery，2009，24(3):1014 －1020.

［3］彭疆南，孙元章，王海风.考虑系统完全可观性的PMU优化配置方法.电力系统自动化，2006，27(4):10 －16.

［4］Tarjan R.Depth first search and linear graph algo － rithms［J］.SIAM Journal of Comput，1972，1(2):146 －160.

［5］Goodaire E G，Parmenter M M.Discrete mathematicswith graph theory［M］.Prentice Hall，1998.

［6］王海英，黄强，李传涛，等.图论算法及其Matlab实现［M］.北京:北京航空航天大学出版社，2010.

［7］许国根，贾瑛.模式识别与智能计算的Matlab实现［M］.北京:北京航空航天大学出版社，2012.