基于金融网络与关键社团的投资组合比较研究

王惠平，韩 华，李 艳

(武汉理工大学 理学院，湖北 武汉430070)

证券投资组合，是由投资者对各种证券资产的选择而形成的，它的意义在于以多种证券作为投资对象，采取适当的方法，在达到预期收益的前提下使投资的风险最小，或者在控制风险的前提下使收益最大。MARKOWITZ［1］的均值-方差模型对于投资组合领域的研究具有开创性的贡献，但由于其在实际应用中的计算量大并且非常复杂，至今在解决大规模证券投资组合问题中尚未得到广泛应用。近年来有一些学者探讨了投资组合样本的选择问题，一般选取市场代表性好，流动性高，具有代表性的行业的证券作为投资组合的样本。刘红明［2］认为沪深300 指数覆盖了大部分流通市值，能够反映市场主流投资的收益情况，因此选取沪深300 指数中数据相对比较完整的200只股票的日收益率作为投资组合的样本。蔡冰晶［3］认为股票在选择的时间段内(1995—2010年)的交易数据相对比较完整，更符合均值-方差模型的市场假设，因此在A 股市场中随机选取10 只属于不同行业的股票作为投资组合的样本。王贞［4］认为沪深300 指数可以近似反映中国股市的涨跌情况，因此选择沪深300 指数下的300 只股票的周收益率作为投资组合的研究对象。徐绪松等［5］选取在各行业中具有代表性的15 只股票作为投资组合的样本。郭海峰等［6］为了使投资者具有更多的投资选择，选取不同行业的20 只股票的100 个周收盘价数据作为样本。TOLA［7］运用纽约交易所的大多数被资本化的150 只股票数据构建投资组合。RUPAK 等［8］选取孟买证券交易所能代表12 个主要行业的30 只股票作为投资组合的样本。

金融市场是一个具有相互作用单元的复杂系统，在金融研究中，相关系数矩阵在构建金融网络中起着很关键的作用，在研究投资组合优化中也是非常重要的。但在实证的相关系数矩阵中会包含大量的噪声信息，这将对研究网络的拓扑结构和投资组合优化造成一定的影响。因此基于随机矩阵理论去除网络中的“噪声”信息是必要的。

在复杂网络研究中，网络中的社团可以看作大规模网络的一种降维方式，社团对应着金融系统中拥有共同角色或者特征的团体。通过寻找和研究网络中的社团结构，可以帮助人们更容易地对网络的整体与各个区块间的联系进行理解，进而对网络的拓扑性质进行研究。笔者首先基于随机矩阵理论对相关系数矩阵进行改进，构建金融网络，再利用GN 算法划出网络的社团，寻找出网络的关键社团，最后以关键社团为研究对象，运用原始矩阵和随机矩阵“去噪”后的相关系数矩阵分别构建投资组合的均值-方差模型，对“去噪”前后投资组合的风险进行比较。

1 金融网络的构建

1.1 相关系数

网络的节点代表股票，边代表股票之间的相关性。Pi(t)为第i只股票在时间t时的收盘价格，股票i的对数收益率的定义如下：

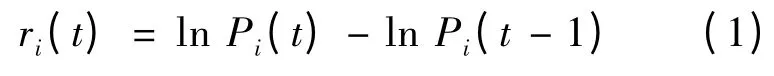
任意两只股票i和j的皮尔逊相关系数为：

其中：＜… ＞为统计平均;ρij的取值范围为［-1，1］。若两只股票完全负相关，则ρij= -1;若两只股票完全正相关，则ρij=1;若两只股票不相关，则ρij=0。利用式(1)和式(2)可以得到股票市场的股票相关系数矩阵C，其大小为N×N，其中的元素是由ρij组成的。

1.2 基于随机矩阵对相关系数进行改进

运用随机矩阵理论，计算得到随机矩阵的预测最大特征值和最小特征值为：

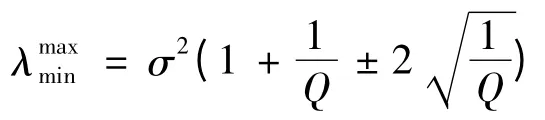
由上述分析可知，金融相关系数矩阵全部特征值中属于［λ-，λ+］的部分代表噪声。

对相关系数矩阵C进行谱分解有：C=PΛPT，其中P为正交矩阵满足条件(PPT=1 )，而Λ 为对角矩阵，PT为矩阵的转置，特征值矩阵Λ=diag{λ1，…，λK}，对特征值λ 可以按照从小到大的顺序进行重新排列，即λ1，…，λt，λt+1，…，λk，λk+1，…，λK，令λk+1＞λmax，且λt＜λ-，令：

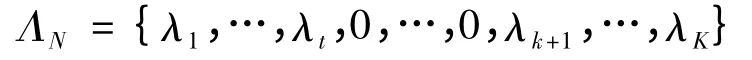
RMT 过滤相关矩阵的基本方法是将相关系数矩阵在随机矩阵理论预测范围内的特征值替换为0。同样特征值矩阵也只留下了相应的特征向量，则新的相关系数矩阵为：

其中PNew为新的特征向量矩阵，此外令对角元素

1.3 社团划分

社团结构定义为内部节点之间的连边数目比节点与外部连边数目大的网络子图，它是网络的中观结构，也是网络拓扑结构和网络组成研究的重要特征［9-10］。

NEWMAN 等首先提出模块度评价函数的概念［11］，它是用来衡量社团结构划分好坏的重要测度。模块度的定义如下：

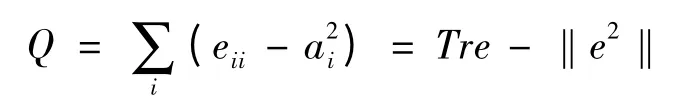
笔者选择道琼斯中国88 指数2011 年11 月1日到2013 年5 月31 日的日收盘价格数据，基于“去噪”方法对相关系数矩阵进行改进，采用边相关系数阈值法［13］，构建金融网络模型。

根据GN 算法对构建的道琼斯中国88 指数股票网络进行社团划分，划分的Q值如表1 所示，当社团个数为11 时，Q=0.004，Q值最大，因此将道琼斯中国88 指数股票网络划分为11 个社团，可以得到如图1 所示的社团结构。在图1 中可以看到该网络有一个关键的社团，它的节点数在整个网络中的比例为85%，在道琼斯中国88指数股票网络中具有影响力的行业都在该关键社团内，因此，对该关键社团进行研究是有意义的。

表1 道琼斯股票网络的Q 值

图1 道琼斯88 中国指数股票的社团结构

笔者以这个关键社团为研究对象，用关键社团的75 只股票作为构建投资组合的样本。

2 马科维茨均值-方差模型构建

2.1 马科维茨均值-方差模型

假设投资者可选择的投资资产有n种，第i种风险资产的期望收益率为Ri，期望收益率用R =(R1，R2，…，Rn)T表示;n种资产收益率的协方差矩阵为S =(δij)n×n;w =(w1，w2，…，wn)T表示一个投资组合，其中wi表示资产在第i种证券上的分配比例，且∑wi =1;n维列向量In =(1，1，…，1)T；为投资组合收益率的方差，用于衡量投资组合的风险;Rp为投资者的目标收益水平。因此Markowitz 模型可表示为：

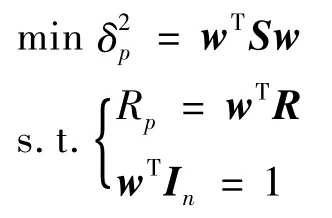
2.2 模型构建

用关键社团的75 只股票作为投资组合的研究对象。将道琼斯中国88 指数2011 年11 月1日到2013 年5 月31 日的数据等分为前后两个时期，首先利用前期数据对后期的风险和收益进行预测，然后将预测结果与后期计算出的实际风险和收益进行比较，在这个过程中，假设投资者可以对未来的平均收益进行准确的预测。具体步骤为：①将投资组合的样本数据分为两个等长记录计算相关矩阵。②应用随机矩阵理论对原始收益数据进行“去噪”。③分别使用“去噪”前后的样本收益数据构建投资组合，并求出最优投资组合。④对“去噪”前后风险分散能力进行比较。

3 投资效果分析

3.1 风险的比较

在比较投资组合优劣时，需要注意风险和收益两个方面。在投资组合收益相同的情况下，最优投资组合决策对应的方差(风险)越小，说明这种方法对风险的分散效果越好，这种方法也就越优。相反，这种方法对风险的分散效果越差，该方法也就越劣。

将风险作为收益Rp的函数，风险大小会随着收益的大小发生变化。收益风险函数可表示为：

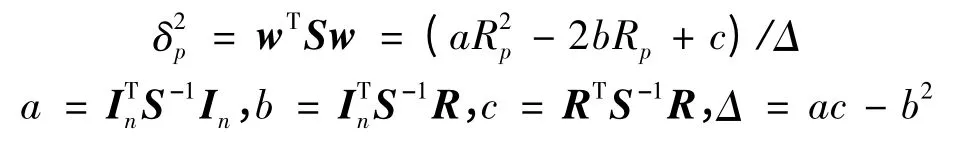
实际风险收益曲线和预测风险收益曲线如图2 和图3 所示。从图2 和图3 中可以看出，与“去噪”前相比，“去噪”后相关矩阵构建的投资组合在预测风险和实际风险方面都有明显降低。在相同的收益下，“去噪”后相关矩阵构建的最优投资组合的风险要小于“去噪”前构建的最优投资组合的风险。而在相同的风险下，“去噪”后相关矩阵构建的最优投资组合的收益要大于“去噪”前构建的最优投资组合的收益。与“去噪”前所作的投资决策方案相比，“去噪”后的投资组合最优决策风险(方差)有了显著降低，由此可见，对价格收益数据进行“去噪”处理更有利于在投资决策中分散风险。

图2 实际风险收益曲线

图3 预测的风险收益曲线

3.2 可靠性比较

从表2 中明显可以看出，用随机矩阵“去噪”后的差异系数的均值是0.059 6，而用原始矩阵得到的差异系数的均值是0. 084 8。用随机矩阵“去噪”后的投资组合的差异系数要比原始矩阵的投资组合的差异系数小，说明用随机矩阵“去噪”后构建的投资组合模型的风险小，更有利于在投资决策中分散风险。

4 结论

笔者将股票视为节点，股票间的相关性视为连边，基于“去噪”方法对相关系数矩阵进行改进，构建金融网络模型，寻找到关键社团，然后以关键社团为研究对象构建投资组合，通过对“去噪”前后构建的投资组合模型对比分析发现，基于“去噪”后相关矩阵构建的投资组合模型比原始相关矩阵构建的投资组合模型更能有效地分散风险，分散效果比较好，从而能对我国股票投资组合风险进行有效地控制。

表2 实际风险与预测风险的差异系数

［1］MARKOWITZ H. Portfolio selection［J］.The Journal of Finance，1952，7(1)：77 -91.

［2］刘红明.基于随机矩阵理论的股票收益相关矩阵分析［D］.杭州：浙江工商大学图书馆，2011.

［3］蔡冰晶.马克维茨均值方差模型在中国股票市场的应用［D］.上海：复旦大学图书馆，2012.

［4］王贞.几类投资组合优化模型及算法［D］.西安：西安电子科技大学图书馆，2012.

［5］徐绪松，宋奇，马莉莉.基于代表性偏差的行为投资组合模型及实证［J］. 系统工程理论与实践，2012，32(1)：34 -40.

［6］GUO H F，SUN B Q，JIN W Q. Fuzzy investment portfolio selection models based on interval analysis approach［J］. Mathematical Problems in Engineering，2012(12)：1 -15.

［7］TOLA V，LILLO F，GALLEGATI M，et al. Cluster analysis for portfolio optimization［J］. Journal of Economic Dynamics and Control，2008，32(1)：235 -258.

［8］RUPAK B，SAMARJIT K，DWIJESH D M. Fuzzy mean-variance-skewness portfolio selection models by interval analysis［J］. Computers ＆ Mathematics with Applications，2011，61(1)：126 -137.

［9］GULBAHCE N，LEHMANN S. The art of community dtection［J］.Bioessays，2008，30(10)：934 -938.

［10］刘晓霞，王卫华.上海证券市场股票网络的复杂网络特性研究［J］.武汉理工大学学报：信息与管理工程版，2012，34(5)：642 -645.

［11］NEWMAN M E J，GIRVAN M. Finding and evaluating community structure in networks［J］. Physical Review E，2004，69(22)：1 -15.

［12］解诌，汪小帆.复杂网络中的社团结构分析算法研究综述［J］.复杂系统与复杂性科学，2005，2(3)：1-12.

［13］蔡世民，洪磊，傅忠谦，等.基于复杂网络的金融市场网络结构市场研究［J］. 复杂系统与复杂性科学，2011，8(3)：29 -33.