时变时延混沌系统的广义函数投影同步

巩长忠，蔡晓东

（中国民航大学理学院，天津 300300）

时变时延混沌系统的广义函数投影同步

巩长忠＊，蔡晓东

（中国民航大学理学院，天津 300300）

研究两个带有时变时延混沌系统的广义函数投影同步（GFPS）问题，其中驱动系统和响应系统是基于一个变换矩阵渐近同步的.基于LaSalle不变原理和Lyapunov稳定性理论，得到使这两个系统同步的充分条件，并用Matlab软件进行数据仿真，验证了方法的有效性.

广义函数投影同步；混沌系统；时变时延；自适应控制

自从混沌同步问题提出以来，许多研究涉及到混沌同步现象，例如完全同步（CS）［1］、广义同步（GS）［2］、延迟同步（LS）［3］、投影同步（PS）［4－6］等.在一系列混沌同步现象中，投影同步由于其更快的反馈速度特征而得到广泛关注，Li Zhenbo［7］，Li Chunlai［8］，Wu Xiangjun［9］等对超混沌系统的广义函数投影同步问题进行了进一步探讨.而在实际问题中，系统中一般存在着不可忽视的时间延迟，时延会彻底改变系统中动力学行为之间的相互作用，因此，为了更好地模拟现实情况，须把时延条件加入到系统模型中.Wu Xiangjun等［10］曾对两个带有时延混沌系统的广义函数投影同步（GFPS）问题进行分析，并用合适的自适应控制器实现了两系统的同步，但其考虑的时延为定值.在本文中，笔者拟基于LaShall不变原理和Lyapunov稳定性理论，探讨两个带有时变时延混沌系统的广义函数投影同步问题，通过构造自适应控制器实现两系统的同步.

1 问题描述

假设把一个时变时延的混沌系统作为驱动系统，其模型可表示为

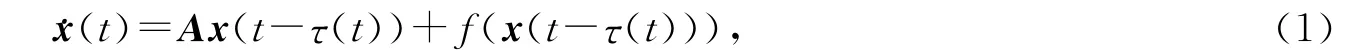
响应系统模型为

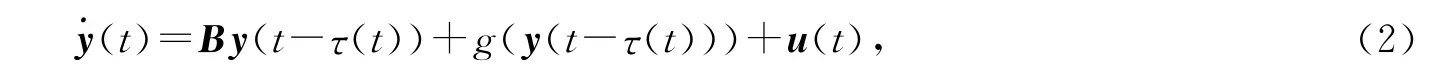
其中x（t）＝（x1，x2，…，x n）T，y（t）＝（y1，y2，…，y n）T∈Rn是相应于系统（1）和（2）的静态变量，A和B是维数适当的常数矩阵，f，g：Rn→Rn是两个非线性连续函数，时变时延τ（t）为非负函数，且满足0≤˙τ（t）≤ε＜1，ε是一常数，u（t）是控制器.

定义1（GFPS） 假设对于系统（1）和（2）中相应的变量为x（t）和y（t），存在一合适的控制器使得limt→∞‖y（t）－P（t）x（t）‖＝0成立，那么称系统（1）和（2）达到广义函数投影同步，其中P（t）＝diag（α1（t），α2（t），…，αn（t））为变换矩阵，αi（t）≠0（i＝1，2，…，n）是有界的连续可微函数.

2 主要结果

引理1 对于任意向量x，y∈Rn和可逆正定矩阵Q∈Rn×n，以下矩阵不等式成立：2xTy≤xTQx＋yTQ－1y.

定义系统（1）和（2）之间的同步轨道误差向量为

为了使系统（1）和（2）达到同步，须构造一个合适的控制器u（t），使得limt→∞‖e（t）‖＝0.

定理1 由已知的非零变换函数αi（t）（≠0）和时变时延函数τ（t），系统（1）和（2）在控制器

下可以达到广义函数投影同步，其中˙k＝μeT（t）e（t），μ是任意正常数.证明 对误差向量e（t）求导得

将式（1），（2），（4）代入式（5），得

构造Lyapunov函数

WHO调查了近年来29个发展中国家的普通孕妇中子痫前期发病率0.02%～7.67%，平均发病率为2.16%。针对正常孕妇的子痫前期试验，发病率不高。Valio等[15]研究了妊娠35～37周的3 953例单胎普通孕妇，最终只有65例发展为子痫前期。一些针对高危孕妇进行的研究中，子痫前期的发病率明显上升[11]。本研究中的研究对象为子痫前期高危孕妇，271例病人中有11例发病，明显提高了sFlt-1、PLGF对于子痫前期的预测价值。早期诊断子痫前期，尽早对于高危孕妇进行干预及监管，减少不良围产期母婴结局的发生具有重要意义。

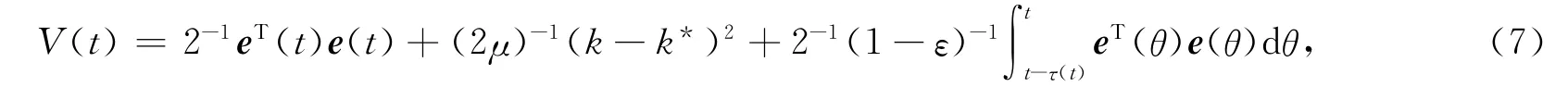
对Lyapunov函数求导，并将误差系统（6）代入其中，由引理1可得

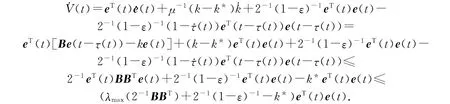
显然存在一个足够大的正常数k＊，即k＊＝λmax（2－1BBT）＋2－1（1－ε）－1＋1，使得˙V（t）≤－eT（t）e（t），即˙V（t）≤0.包含于E＝｛˙V（t）＝0｝＝｛e（t）＝0｝的最大不变集为M＝｛e（t）＝0，k＝k＊｝.由误差系统（6）可知，当t→∞时，e（t）→0，k→k＊，即两个不同的混沌系统（1）和（2）达到了广义函数投影同步.定理证毕.

由定理1可以很容易得到以下推论.

推论1 假如驱动系统（1）和响应系统（2）具有相同的动态，即A＝B，f＝g，由已知的非零变换函数αi（t）（≠0）和时变时延函数τ（t），两系统可在以下控制器作用下达到广义函数投影同步：

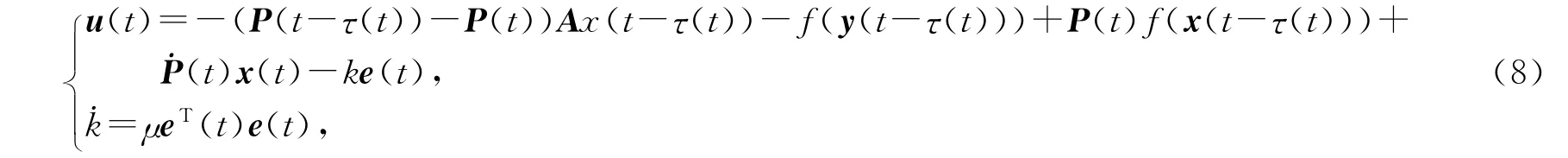
其中μ是任意正常数.

3 数据仿真

本文采用Matlab软件进行数据仿真来验证方法的有效性，混沌系统选用有时延的Lü系统，模型如下：

驱动系统和响应系统的模型分别为

其中ui（t）（i＝1，2，3）是两时变时延混沌系统实现广义函数投影同步的控制器.定义GFPS误差向量为

其中αi（t）（i＝1，2，3）为非零缩放函数.

由推论1中的公式（8）可以得到控制器为

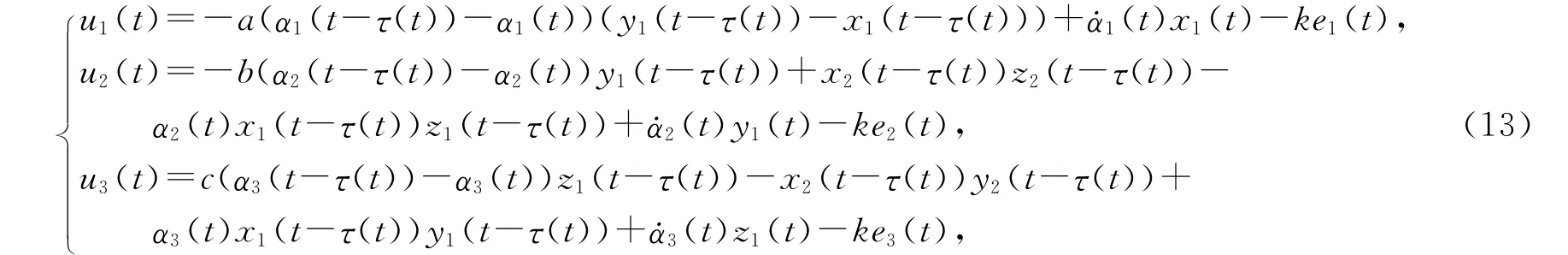
为了保证混沌行为的存在，Lü系统中a＝36，b＝20，c＝3；驱动系统（10）和响应系统（11）的初值设为0到1之间的随机值；k的初值设为k（0）＝0.01，μ的 取 值 为 2；缩 放 函 数 选 取α1（t）＝1.5＋sin（0.5t），α2（t）＝2－0.5cost，α3（t）＝ －2＋sin（5t）；时变时延函数设为τ（t）＝0.01t.

采用Matlab软件进行数据仿真，由图1可以看出，两系统的误差向量e1（t），e2（t），e3（t）迅速收敛到0，也就是说两系统达到了广义函数投影同步.

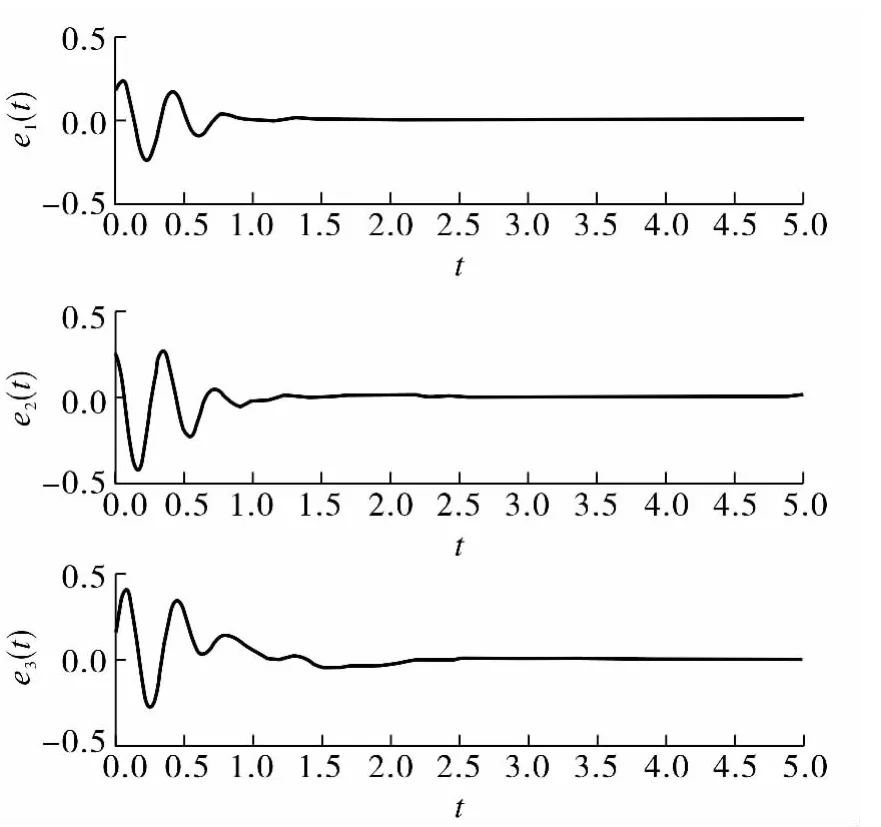
图1 Lü系统（10）和（11）的误差曲线Fig.1 Errors between Lüsystem （10）and（11）

［1］PECORA L M，CARROLL T L.Synchronization in chaotic systems［J］.Phys Rev Lett，1990，64（8）：821－824.

［2］GE Zhengming，CHANG Chingming.Generalized synchronization of chaotic systems by pure error dynamics and elaborate Lyapunov function［J］.Nonlinear Anal：Theor Meth Appl，2009，71（11）：5301－5312.

［3］LI Chuandong，LIAO Xiaofeng，WONG Kwokwo.Chaotic lag synchronization of coupled time－delayed systems and its applications in secure communication［J］.Phys D：Nonlinear Phenom，2004，194（3／4）：187－202.

［4］MAINIERI R，REHACEK J.Projective synchronization in three－dimensional chaotic systems［J］.Phys Rev Lett，1999，82（15）：3042－3045.

［5］XU Daolin.Control of projective synchronization in chaotic systems［J］.Phys Rev E，2001，63（2）：027201：1－4.

［6］赵磊，胡冯仪，郑永爱，等.不同混沌系统的自适应混合投影同步 ［J］.扬州大学学报：自然科学版，2008，11（3）：45－48.

［7］LI Zhenbo，ZHAO Xiaoshan.Generalized function projective synchronization of two different hyperchaotic systems with unknown parameters［J］.Nonlinear Anal：Real World Appl，2011，12（5）：2607－2615.

［8］LI Chunlai.Generalized function projective synchronization and tracking control of a class of hyperchaotic systems with unknown parameters and disturbance［C］／／2011 Second International Conference on Mechanic Automation and Control Engineering（MACE）.Hohhot：IEEE，2011：1336－1338.

［9］WU Xiangjun，GUO Nian.Generalized functional projective synchronization of a new hyperchaotic system based parameters identification［C］／／2011 Third Pacific－Asia Conference on Circuits，Communications and System（PACCS）.Wuhan：IEEE，2011：1－4.

［10］WU Xiangjun，WANG Hui.Generalized function projective synchronization of a class of delayed chaotic systems［C］／／2010 International Workshop on Chaos－Fractals Theories and Applications（IWCFTA）.Kunming：IEEE，2010：48－52.

Generalized function projective synchronization of a class of chaotic systems with time－varying delays

GONG Changzhong＊，CAI Xiaodong

（Coll of Sci，Civ Aviat Univ of China，Tianjin 300300，China）

Generalized function projective synchronization（GFPS）of a class of chaotic systems with time－varying delays is studied in this paper，where the drive and response systems are asymptotically synchronized up to a scaling function matrix.Based on LaSalle theory and Lyapunov stability theory，the sufficient condition is obtained to achieve GFPS between two different chaotic systems.Numerical simulations using Matlab are presented to verify the effectiveness of the proposed scheme.

generalized function projective synchronization；chaotic systems；time－varying delay；adaptive control

TP 273.2

A

1007－824X（2014）01－0056－04

2013－10－14.＊ 联系人，E－mail：g－chzh＠163.com.

中央高校基本科研业务费资助项目（ZXH2012B003，ZXH2012K002）；天津市自然科学基金青年项目（13JCQNJC－04400）.

巩长忠，蔡晓东.时变时延混沌系统的广义函数投影同步 ［J］.扬州大学学报：自然科学版，2014，17（1）：56－59.

（责任编辑 时 光）