带时间窗的多配送中心多车型车辆调度问题

高珊珊，李萌萌

(1.兰州商学院 管理科学与工程学院，甘肃 兰州730020;2.兰州商学院 统计学院，甘肃 兰州730020)

0 引 言

随着我国经济的快速发展，物流作为社会经济活动的基础，被称为企业的“第三利润源泉”［1］。物流业的发展与进步受到了越来越多的重视，因此物流产业的专业化程度也不断的提高。配送方案的合理与否对物流成本、效益、服务水平以及顾客的满意度都有着重要的影响。本文针对物流配送路径问题进行研究。合理选择最优的配送路径，以减少配送时间、节约配送成本、提高服务质量、增加经济效益以及提高顾客满意度。

车辆路径问题(Vehicle Routing Problem)是1959年由Dantzig 和Ramser 提出的［2］，该问题在现实生活中的应用相当广泛。近几年越来越多的人对其进行优化研究，然而现实路径中存在很多的约束条件，如:配送中心的多少、配送车辆的类型、客户对时间的要求、客户需求的随机性、动态道路堵车情况等，在研究模型中考虑的约束条件越多则研究结果越接近现实路径问题。

目前对多约束条件车辆调度问题的研究有:文献［4］等人用两阶段法研究了多配送中心问题;文献［1］考虑了车容量的限制，即对车型问题进行了研究;文献［10］考虑的带时间窗的约束;文献［7］在时间窗的基础上加入了非满载条件;文献［3］考虑了带时间窗的多配送中心约束条件。本文在已有研究的基础上，用改进的节约法研究了带时间窗的多配送中心多车型的车辆调度问题。(1)针对模型利用重心法把客户分配到不同的配送中心，每个配送中心的客户是确定的，然后建立多配送中心多车型的VSP 数学模型，模型基于配送费用最少为目标函数。(2)对各个分配送中心应用改进的节约算法进行求解带时间窗约束的单配送中心车辆调度路径模型。

1 路径调度问题模型建立

1.1 时间窗约束问题

带时间窗约束的车辆调度问题，即为客户对配送任务有时间的要求，要在最早时间ET 与最晚时间LT之间(ET ＜t ＜LT)进行配送活动。时间窗问题可以分为硬时间窗和软时间窗两种。对于硬时间窗问题，车辆必须在时间窗［ET，LT］内进行配送，在时间窗外客户则不接受货物配送，即得到的解为不可行解。而对于软时间窗问题。如果车辆早于ET 到达，则需等到ET 再进行配送，此时需要承担一定的成本损失，若迟于LT 到达，则要承担一定的惩罚费用，若过早或过迟，客户将不接受配送，即又变成了硬时间窗问题，此时需要一个无穷大的惩罚成本L 来表示。本文采用软时间窗约束来求解［3］。其惩罚成本可表示如下:

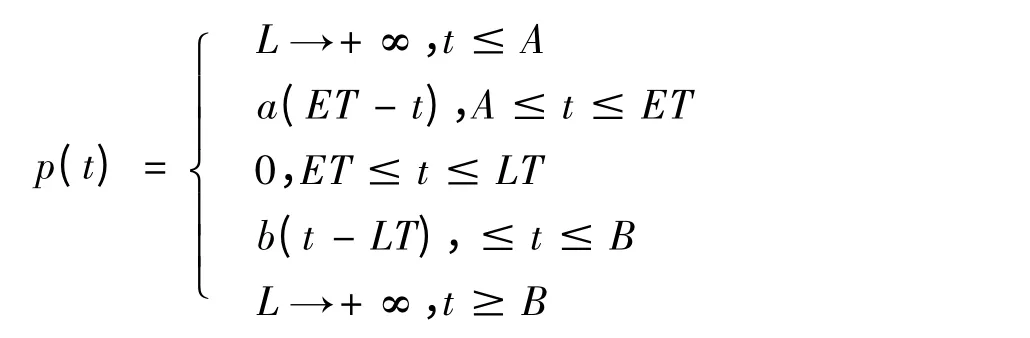
其中，p(t)是有时间窗约束所引起的惩罚成本;A 为可接受的最早等待时间，a 为等待时产生的成本系数;B 为可接受的最晚时间，b 为延迟送货需要承担的惩罚成本系数;L 为无穷大的惩罚成本。

1.2 问题与约束条件

物流配送路径优化问题可以描述为:某配送中心需要多台车向此分区的多个客户提供送货。客户和配送中心的位置确定，且每个客户对货物的需求量确定。每个配送中心有多种车型，每种车型载货量确定，最大行驶距离确定。每辆车可以为多个客户服务，每个客户只能有一辆车提供服务，车辆从配送中心出发完成配送任务后返回原配送中心。配送中心要在客户规定的时间内将货物送到。要求合理调度车辆安排配送路径，使目标函数即配送费用最小得到优化。问题的基本约束条件如下:

(1)有多个配送中心，每个配送中心有多种车型;

(2)配送中心车型不同，载重量不同，最大行驶距离不同;

(3)配送中心对客户的配送需求和位置是已知的;

(4)每个客户的实际需求量不超过每种车型的最大载货量，一次配送任务的总距离不大于配送车辆一次行驶的最大距离;

(5)每辆车仅调度一次，每个客户只能有一辆车进行配送，车辆从配送中心出发最后又回到原配送中心。

(6)客户要求在一定的时间范围内把货物送到，即考虑时间窗约束。

1.3 VSP 模型的建立

由以上的约束条件可以将多配送中心多车辆的VSP 的数学模型设计如下:

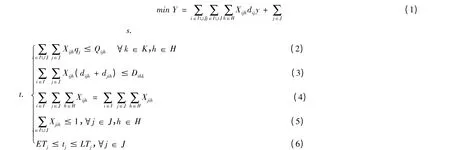
其中，I 为配送中心集合，i 为各分配送中心;J 为客户集合，j 为客户;H 为车辆集合，h 为各车辆;K 为车型集合，k 为车型;qj为j 客户的需求量，Qihk为i 配送中心的h 车辆为k 车型的最大载重量;dij为i 配送中心到j 客户的距离，Dihk为i 配送中心h 车辆为k 车型的最大行驶距离;y 为单位货物单位里程的运输费用;p(t)为时间窗约束的惩罚成本;Xijh为i 配送中心的h 车辆为j 客户提供服务，若为1 即参与配送，反之为0。

上述模型中:式(1)为目标函数，即要求配送费用最小;式(2)－－(6)为模型的约束条件。其中式(2)为j 客户的需求量不大于i 配送中心k 车型h 车辆的最大载重量;式(3)为i 配送中心h 车辆完成一次配送任务的距离不大于此配送车型的最大行驶距离;式(4)为车辆若参与配送最后要返回原配送中心;式(5)为一辆车只能从配送中心调度一次，且一个客户只能有一辆车进行配送;式(6)客户要求进行配送的时间约束。

2 重心法分区算法

2.1 重心法介绍

本文研究的是大规模的车辆配送问题，由于配送距离远，道路的动态状况，单配送中心已经不能满足货物的及时有效的配送，因此多配送中心被广泛的应用。本文将运用几何重心的分区方法将多配送中心问题分成各个单配送中心问题来解决，大大的提高了多配送中心车辆调度的效率。

重心分区法是以连接所有配送中心的几何重心和相邻两个配送中心的中点的做中垂线将配送中心分为不同的区域［4］。有几个配送中心将会得到几个分区，每个分区内的客户是确定的。各个配送中心的路径互不交叉、业务相互独立，且操作简单，大大减少了计算量，在大规模多配送中心问题中有很大优势。

2.2 算法步骤

(1)确定各个配送中心的位置，计算所有配送中心的重心位置O;

(2)将O 与两两配送中心连线的中线做中垂线;

(3)相邻两条射线围成的区域即为在此区域内配送中心的配送范围，垂线上的点归为右侧。

2.3 算例描述

设有2 个配送中心，10 个客户，其位置坐标如下表一所示。用重心法进行分区，可得配送中心I1的客户为4 个:1，3，9，10;配送中心I2的客户为6 个:2，4，5，6，7，8。

表1 客户与配送中心数据

3 节约算法解决路径优化

3.1 节约算法介绍

C－W 节约算法是1964年Clarke 和Wright 提出的［5］，是为了解决以最短路径为优化目标的问题［6］。其基本思想是:(1)将配送中心与各个客户之间进行连线构成线路Si;(2)任意两个客户之间相连接形成路径Sij，计算节约值Wij=Si+Sj－ Sij，Sij越大则连接后节约的费用约多;(3)将Sij由小到大进行排序依次连接各点，直到Sij=0，即可得到此配送路径的最小总路程［7］。

3.2 改进节约算法设计

由于节约算法最初是为了解决旅行商的问题提出的，因此对路径中的各种约束条件没有加以考虑，故无法直接用以解决VRP 问题，但可以通过改进来完善此算法，文献［8］［9］都是对节约算法的改进，本文通过模型的特点对其进行改进。

3.2.1 软时间窗设计

软时间窗约束主要考虑i 与j 进行连接后，客户i 之后各客户点的货物到达时间变化ij=Wij/v 所引起的惩罚成本P()。将惩罚成本与减少的里程费用进行比较确定是否进行此次连接。具体步骤如下:

(1)减少的里程费用:Fij=Wij* y=(Si+Sj－ Sij)* y;

(2)时间变化引起的惩罚成本:若ij＜ET，则惩罚成本P()=a(ET－ Tij);若ET ＜Tij＜LT，则P()=0;若ij＞LT，则P()=b(ij－ LT);

(3)若P()＞Fij，证明此次连接引起的惩罚成本大于连接减少的里程费用，则取消此次连接;若P()=Fij，则可连接可不连接;若P()＜Fij，则进行此次连接。

3.2.2 多车型设计

将多种车型加入进行考虑，每种车型的最大容载量Q、最大行驶里程S 以及单位公里的行驶费用y 都不同，而车辆的行驶速度v 一定。在连接Sij之前先计算连接后的车载量与行驶总里程是否超过此车型的最大容载量及最大行驶里程［10］。若不超过则进行下一个连接，若超过则不连接，结束该路径。

4 实验分析

配送中心与客户信息如表1所示，其中参数设置为:a=1/h ;b=5/h ;y 代表单位里程费用，其中包括燃油费，司机工资等，yk1=1.1/km;yk2=1/km;车型容量Ck1=8t;Ck2=4t;最大行程:Sk1=15;Sk2=10;车速v=2;卸货时间统一为10min;用节约法进行路径优化求解可得:

配送中心I1的路径L1:I1－ K1－1－3－10－ I1;L2:I1－ K2－9－ I1;

配送中心I2的路径L3:I2－ K1－4－6－2－5－ I2;L4:I2－ K2－8－7－ I2;

L1，L2表示配送中心1 派2 辆车K1，K2分别为1，3，10 和9 服务后返回配送中心1;L3，L4表示配送中心2 派2 辆车K1，K2分别为4，6，2，5 和8，7 服务后返回配送中心2。完成路径L1所需费用:F11=Si1k1* yk1=11.708* 1.1=12.879;同理可得L2，L3，L4的费用为F12=Si1k2* yk2=6.325* 1=6.325;F21=Si2k1* yk1=14.307* 1.1=15.738;F22=Si2k2* yk2=7.634* 1=7.634。

其在路径L1中K1到达客户1 的时间10:30［9:45－10:45］，即不产生惩罚成本;K1到达客户3 的时间为11:47［12:30－－13:00］，即产生等待惩罚成本P(t)=43/60* 1=0.716;客户10 的时间属于全天，即不产生惩罚成本;则路径L1产生的惩罚成本为P(t)=0.716;同理可得L2无惩罚成本;L3的延迟惩罚成本为:P(t)=17/60* 5=1.417;L4产生的等待惩罚成本为:P(t)=8/60* 1=0.133。

以上实验模型具有2 个配送中心2 种车型10 个客户数且带软时间窗约束，用节约法进行路径优化可得:整个配送网络共派出4 辆车，2 辆K1和2 辆K2;总路程长为39.974km;最小费用minY=F+P(t)=39.11+2.266=41.376。

通过以上实验分析可知，对于带软时间窗的多配送中心多种车型的车辆调度问题可以用此改进的节约算法进行优化，以实现配送车辆最少、总路程最短，从而实现配送费用最小的目标。

5 结 语

论文在研究多配送中心多车型的车辆调度问题的基础上，考虑了更接近现实情况的软时间窗约束，并结合模型特点用重心法先对多配送中心进行分区变成各个单配送中心，然后对传统节约算法进行改进，加入了多车型与软时间窗约束条件对单配送中心模型进行求解。最后用实验分析验证了此改进的节约算法对此模型的有效性。

［1］占焱发.基于遗传算法的物流配送车辆路径问题研究［D］.陕西:长安大学硕士学位论文，2010.

［2］Golden B L.Transportation planning models［M］.Amsterdam:Elsevier Science Publishers，1984:384－418.

［3］施朝春，王 旭，葛显龙.带有时间窗的多配送中心车辆调度问题研究［J］.计算机工程与应用，2009，45(33):21－24.

［4］陈诚，李正红.多配送中心车辆路径问题的两阶段算法［J］.三明学院学报，2010，27(6):517－520.

［5］Clarke G，Wright J.Scheduling of vehicles from a central depot to a number of delivery points［J］.OperationResearch，1964，12(4):12－18.

［6］李远远，刘彦，刘光前.车辆路径问题优化——基于改进节约算法［J］.社会科学家，2013，11(9):76－79.

［7］宋伟刚，张宏霞，佟 玲.有时间窗约束非满载车辆调度问题的节约算法［J］.科技导报，2006，27(1):65－68.

［8］Golden B，Assad A，Levy L，et al.The fleet size and mix vehicle routing problem［J］.Comps.Opns.Res.，1984，11:49－66.

［9］Ferland J A，Michelon P.The Vehicle scheduling problem with multiple vehicle types［J］.Operational Research Society，1988，39(6):577－583.

［10］崔宏志，龚加安.带时间窗车辆路径问题的改进节约算法［J］.纯粹数学与应用数学，2011，27(5):688－693.

［11］陈一永，许力.C－K 节约算法在配载车辆调度问题上的应用研究［J］.商场现代化，2009，56:149.

［12］张建同，冯子炎.求解车辆路径问题的改进CW 节约算法［J］.物流技术，2012，18(2):75－83.