输入状态稳定理论下的超混沌系统同步

颜闽秀 郑小帆 闫明

(沈阳化工大学信息工程学院1,辽宁 沈阳 110142;辽宁大学轻型产业学院2,辽宁 沈阳 110136)

输入状态稳定理论下的超混沌系统同步

颜闽秀1郑小帆1闫明2

(沈阳化工大学信息工程学院1,辽宁 沈阳 110142;辽宁大学轻型产业学院2,辽宁 沈阳 110136)

针对一类带不确定性和扰动输入的超混沌系统的同步问题进行了研究。基于李雅普诺夫理论和输入状态稳定理论,设计了一个线性状态反馈控制器,保证两个系统达到同步,并通过Matlab中的LMI工具箱来获得误差反馈增益矩阵。最后,通过对超混沌Lorenz系统和Chen系统同步的Matlab仿真,验证了所设计的控制器的有效性,实现了两个超混沌系统的鲁棒同步。

混沌信号 超混沌系统 鲁棒同步 输入状态稳定性(ISS) 线性矩阵不等式 李雅普诺夫理论 线性状态反馈

0 引言

混沌信号具有非周期性、类似噪声、天然隐蔽性、高度复杂性、长期不可预测性与易于实现等特性,非常适合应用于保密通信。1990年,Pecora和Carroll提出了混沌系统同步[1],实现了同一信号驱动下两个耦合混沌系统的状态同步。此后,研究者们提出了一些新的同步控制方法,如滑模控制方法[2-3]、自适应法[4-5]、主动控制法[6-7]、状态反馈法[8-9]、脉冲同步法[10-11]、观测器法[12-13]等。

1989年,Eduardo D.Sontag针对非线性系统提出了输入-状态稳定(input-to-state stability,ISS)的概念[14],用来消除外部扰动输入带来的影响。随后输入状态稳定的研究得到了广泛的重视[15-17]。然而,这一理论应用到混沌系统同步的成果很少见。

本文针对一类带不确定性和外界扰动的超混沌系统的同步问题进行了输入状态稳定控制研究,设计了线性误差反馈控制器来保证误差系统渐近稳定。最后,通过仿真验证了本文设计的控制器的有效性。

1 同步误差系统的描述

假设驱动系统和响应系统分别为:

式中:x和y∈Rn为系统的n维状态向量;A∈Rn×n为系统的线性部分;f(x),f(y)∈Rn为系统的非线性部分; ΔA∈Rn×n描述的是系统的不确定性;δ1(t)和δ2(t)∈Rn为系统的外部干扰向量;u(t)为控制输入。

同步误差系统可以写成:

则有:

2 线性状态控制器的设计与分析

定理1 对于误差系统(3),如果存在正实数ε、正定的对称矩阵X和任意的矩阵Y,满足下面的线性矩阵不等式(linear matrix inequality,LMI):

系统存在输入状态反馈控制器保证其渐近稳定,并且增益矩阵K=YX-1,证明如下。

选取Lyapunov函数为V=eT(t)Pe(t),其中P＞0且PT=P。将函数对时间求导,得到:

而2xTDF(t)Ey≤εxTDDTx+ε-1yTETEy,则有:

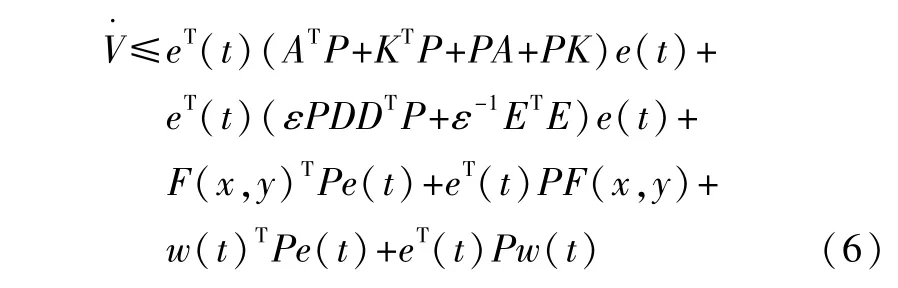
将上述不等式左乘ε,令P=εP,则有:

根据定理,得到下面的不等式:

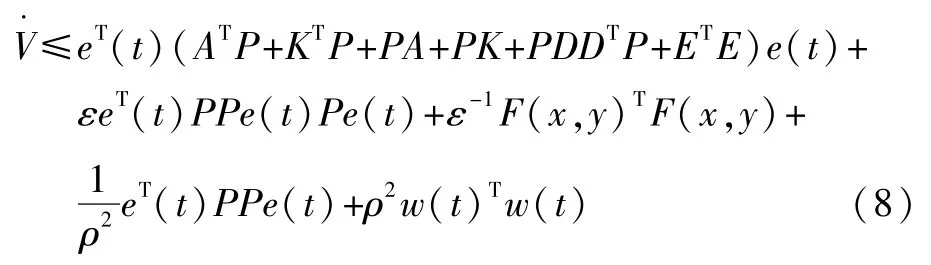
而‖f(y)-f(x)‖≤L‖y-x‖,则可得到:

如果式(10)成立,即:

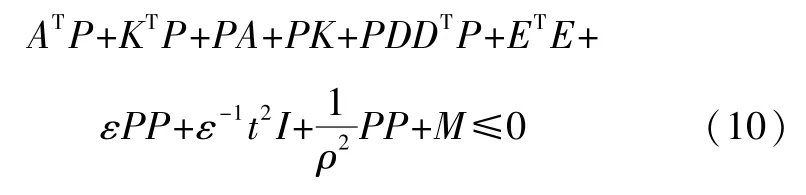
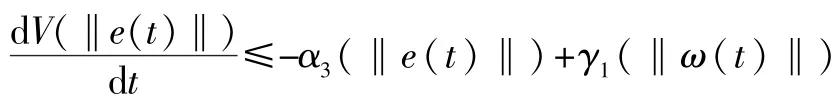
应用Schur补定理,得到下面的线性矩阵不等式:

如果存在整实数ε,正定的对称矩阵X和任意的矩阵Y满足线性矩阵不等式,那么就可实现输入状态稳定控制,并且增益矩阵K=YX-1。

3 仿真分析与讨论

为了验证所设计的同步控制器的有效性,本文选取超混沌Lorenz和Chen系统为例进行研究。超混沌Lorenz系统可以用式(13)来表示,即:

式中:a=10;b=28;c=8/3;d=1.3。

超混沌Chen系统可以用式(14)来表示:

式中:a=35;b=7;c=12;d=3;r=0.5。

3.1 超混沌Lorenz系统的同步

假设

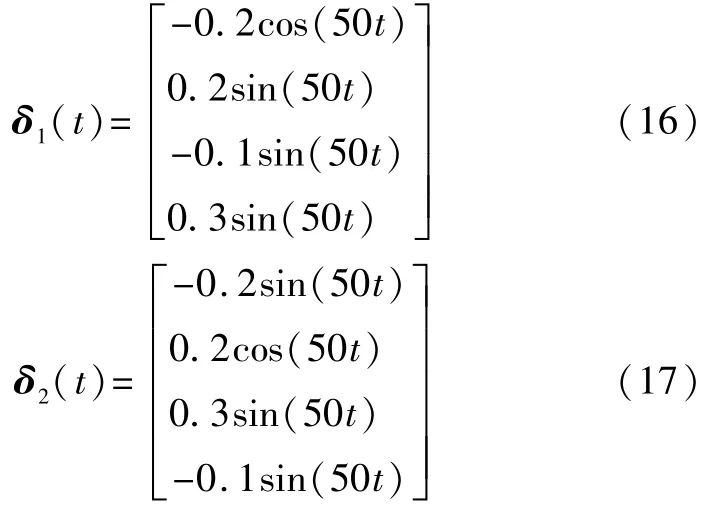
选取驱动系统和响应系统的初始值分别为: [x1(0),x2(0),x3(0),x4(0)]=(1,2,-1,2),[y1(0), y2(0),y3(0),y4(0)]=(-2,2,1,0)。令M=I,ρ=0.1,l= 87。用Matlab中LMI工具箱解线性矩阵不等式,得到增益矩阵:

通过仿真,两个超混沌Lorenz系统的同步误差曲线如图1所示。从图1可以看出,响应系统在10 s施加控制器后渐近跟踪上驱动系统,同步误差也渐近趋向于零。

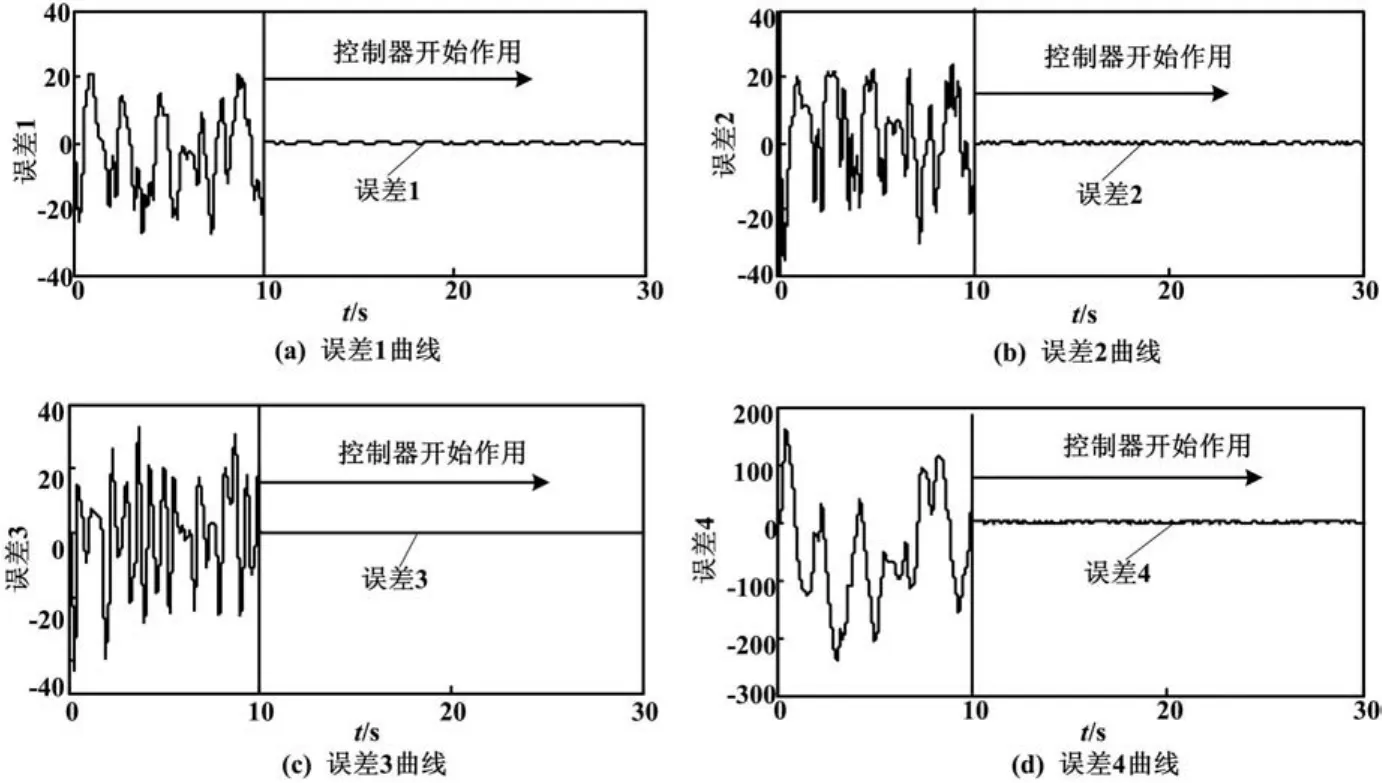
图1 Lorenz系统的同步误差曲线Fig.1 Synchronization error curves of the Lorenz system

3.2 超混沌Chen系统的同步

假设

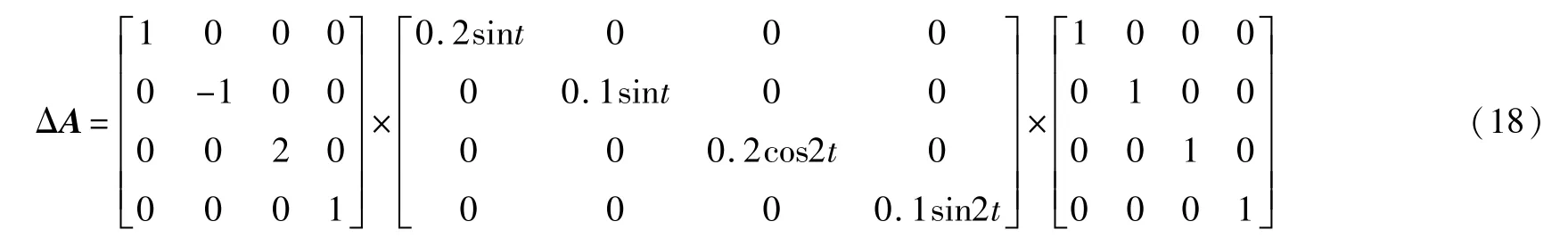
选取驱动系统和响应系统的初始值分别为:[x1(0), x2(0),x3(0),x4(0)]=(2,5,-1,2),[y1(0),y2(0),y3(0), y4(0)]=(-3,1,2,3)。令M=I,ρ=0.1,l=77.5。用Matlab中LMI工具箱得到增益矩阵:

两个超混沌Chen系统的同步误差曲线如图2所示。在外部干扰存在的情况下,未施加控制器时驱动系统不能跟踪响应系统,10 s后施加所设计的控制器,误差状态曲线渐近收敛到零。

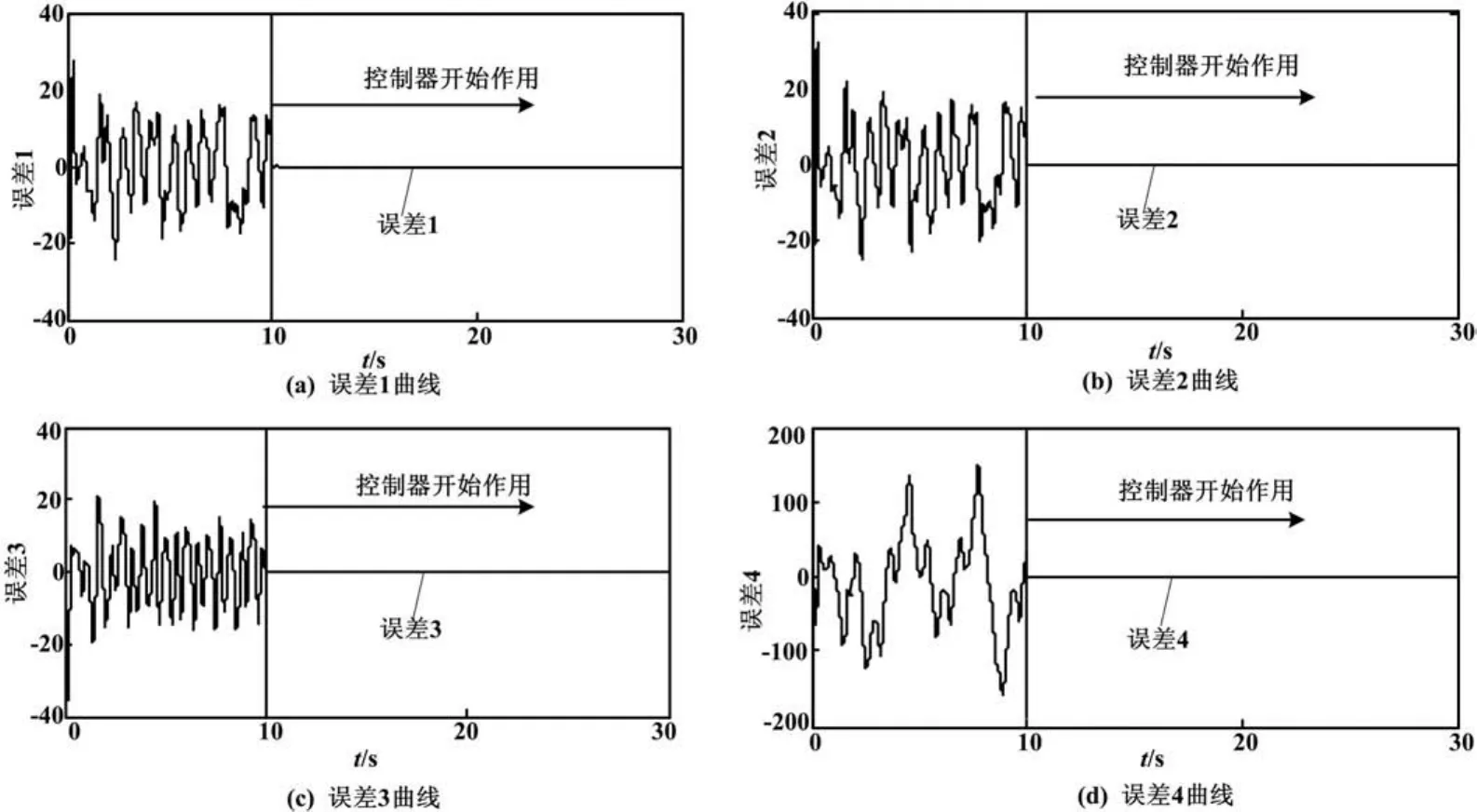
图2 驱动和响应系统的同步误差曲线Fig.2 Synchronization error curves of the slave system and the master system

4 结束语

本文主要研究了一类带不确定性和外部扰动输入的超混沌系统的同步问题。利用输入状态稳定理论和Lyapunov稳定理论,给出了线性误差反馈控制器的设计方法及求解反馈增益矩阵的线性矩阵不等式,并将这种混沌系统同步方法应用于超混沌Lorenz和Chen系统。数值仿真验证了所设计控制器的有效性。该控制器实现了两个超混沌系统的鲁棒同步。

[1] Pecora L M,Carroll T L.Synchronization in chaotic systems[J]. Physical Review Letters,1990,64(8):821-824.

[2] 高远,罗文产,戴喜生,等.不确定性超混沌系统的积分滑模同步控制研究[J].自动化仪表,2012,33(5):15-17.

[3] 李洁,吴忠强.混沌系统的快速收敛有限时间滑模自适应控制[J].自动化仪表,2009,30(11):34-37.

[4] Zhang Jian,Xu Hongbing,Wang Houjun.Adaptive synchronization of Chua's system with uncertain inputs[J].Chinese Physics,2006, 15(5):953-957.

[5] Li X F,Leung A C S,Han X P,et al.Complete(anti-)synchronization of chaotic systems with fully uncertain parameters by adaptive control[J]. Nonlinear Dynamics,2011,63(1-2):263-275.

[6] 颜闽秀,樊立萍.混沌系统的主动自适应滑模修正投影同步[J].自动化仪表,2013,34(2):23-25.

[7] Yassen M T.Chaos synchronization between two different chaotic systems using active control[J].Chaos,Solitons&Fractals,2005, 23(1):131-140.

[8] Chen H H,Sheu G J,Lin Y L,et al.Chaos synchronization between two different chaotic systems via nonlinear feedback control[J].Nonlinear Analysis:Theory,Methods&Applications,2009,70(12):4393-4401.

[9] Ahn C K.T-S fuzzy H∞synchronization for chaotic systems via delayed output feedback control[J].Nonlinear Dynamics,2010, 59(4):535-543.

[10] Jiao H,Qiao Y,Miao J,et al.Exponential synchronization of coupled neural networks with impulsive control[J].Scientific Journal of Control Engineering,2013,3(4)254-260.

[11] Yang X S,Cao J D,Lu J Q.Stochastic synchronization of complex networks withnonidentical nodes via hybrid adaptive and impulsive control[J].CircuitsandSystemsI:RegularPapers,IEEE Transactions on Circuits and Systems,2012,59(2):371-384.

[12] 姚利娜,高金峰,廖旎焕.实现混沌系统同步的非线性状态观测器方法[J].物理学报,2006,55(1):35-41.

[13] 刘虎,张树京,董德存,等.高维混沌同步控制及其在保密通信中的应用[J].自动化仪表,2001,22(10):17-18.

[14] Sontag E D.Smooth stabilization impliescoprime factorization[J]. Automatic Control,IEEE Transactions on Automatic Control,1989, 34(4):435-443.

[15] Liu J,Liu X,Xie W C.Input-to-state stability of impulsive and switching hybrid systems with time-delay[J].Automatica,2011, 47(5):899-908.

[16] Huang S,James M R,Nešic D,et al.Analysis of input-to-state stability for discrete time nonlinear systems via dynamic programming[J]. Automatica,2005,41(12):2055-2065.

[17] Jiang Z P,Wang Y.Input-to-state stability for discrete-time nonlinear systems[J].Automatica,2001,37(6):857-869.

Robust Synchronization of Hyperchaotic Systems under Input-to-state Stability Theory

The synchronization of hyperchaotic systems with uncertainty and disturbance input is investigated.Based on Lyapunov theory and input-to-state stability theory,the linear state feedback controller is designed,to guarantee synchronization of two systems and the error feedback gain matrix is obtained through the LMI toolbox in Matlab.The effectiveness of the controller designed is verified through the Matlab simulation of synchronization for hyperchoatic Lorenz system and Chen system,robust synchronization of two hyperchaotic systems can be implemented.

Chaotic signal Hyperchaotic system Robust synchronization Input-to-state stability(ISS) Linear matrix inequality(LMI) Lyapunov theory Linear state feedback

TP29

A

国家科技支撑计划基金资助项目(编号:2012BAF09B01);

辽宁省自然科学基金资助项目(编号:201202092)。

修改稿收到日期:2014-02-18。

颜闽秀(1972-),女,2009年毕业于东北大学控制理论与控制工程专业,获博士学位,副教授;主要从事变结构控制、智能控制的研究。