一种改进的Alstom气化炉预测控制
杨小龙张正刚丁维明
(东南大学能源与环境学院1,江苏 南京 210000;苏州紫兴纸业有限公司2,江苏 苏州 215011)
一种改进的Alstom气化炉预测控制
杨小龙1张正刚2丁维明1
(东南大学能源与环境学院1,江苏 南京 210000;苏州紫兴纸业有限公司2,江苏 苏州 215011)
Alstom能源技术中心给出了气化炉在全工况下的Matlab非线性模型。为了解决Alstom气化炉非线性、强耦合以及大惯性特点所带来的控制问题,设计了一种模型预测控制器。首先在局部工况点建立离线线性模型,在所建模型基础上设计控制器,应用灰色理论GM(1,1)在误差校正环节预测未来时刻由于模型不匹配产生的误差,以此来提高控制器输出的精度。仿真结果表明,在压力扰动测试中,即使各控制量受到严格的约束,各输出量的偏差仍能维持在规定的范围内,满足了Alstom气化炉的控制要求。
Alstom气化炉 非线性系统 离线建模 模型预测控制 灰色预测误差校正
0 引言
整体煤气化联合循环(integrated gasification combined cycle,IGCC)作为一种高效清洁利用煤炭的方式正日益受到重视,已经成为国内外研究的热点[1]。Alstom能源技术中心基于英国一座联合循环示范电站中的增压喷流床气化炉,建立了该气化炉在全工况范围内的模型,并发布了气化炉控制的基准问题,列出了一系列基准测试项目及其系统控制约束条件。
模型预测控制(model predictive control,MPC)由法国Adersa公司的Richalet于1978年提出,能够用于处理常规PID控制很难处理的问题[2]。模型预测控制是基于线性模型建立起来的,因此在非线性系统中并不总是有效,因为非线性系统很难建立一个偏差较小的线性模型,虽然有时可以用神经网络进行建模,但是数据的庞大使得控制变得不可实现。因此,这里考虑在各个负荷点建立局部线性模型,基于各个典型工况下设计的预测控制器的控制量的叠加,以此来实现非线性系统的全局控制。同时,通过引入灰色预测理论来预测未来时刻的误差范围,能够在扰动条件下使响应更加迅速、超调更小。
1 建模过程以及描述过程
Alstom气化炉模型是基于一台87 MW喷流床气化炉的实时运行数据建立的,因此具有很高的精度。如图1所示是Alstom气化炉简要工作流程。
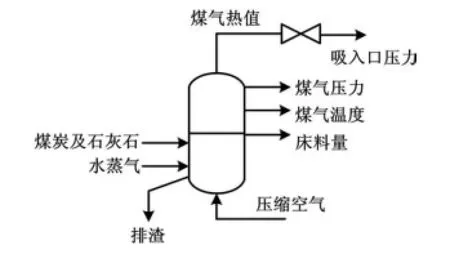
图1 Alstom气化炉的生产流程简图Fig.1 Simplified diagram of the production process of Alstom Gasifier
在该气化炉生产过程中,经过处理的煤粉与吸附剂石灰按一定比例混合,由增压空气和水蒸气运送,喷入气化炉内。在气化炉内,空气和蒸汽对固体进行流化,同时与煤中的碳发生反应,产生热值约为4.5 MJ的低热值煤气。煤气经净化后进入燃气轮机,余下的灰分、石灰以及未完全反应的碳以灰渣的形式从底部排出。可以分析得出,气化炉是一个5输入4输出的系统,由于吸附剂和煤成一定比例,因此可以简化成一个4输入4输出的强非线性和强耦合的多变量系统。控制量为进口空气流量(Qair)、进口蒸汽流量(Qstm)、煤粉流量(Qcoal)以及排渣量(Qchar);被控量为床料质量(M)、煤气热值(CVgas)、煤气温度(Tgas)以及煤气压力(Pgas)。对于气化炉而言,外界的扰动主要是工况的变化,因此,将下游燃气轮机的入口压力波动Psink作为主要的扰动量[3]。
Alstom建立的示范IGCC电站动态机理模型经过了实际数据的严格校验,具有较高的准确度。Alstom在公开动态机理模型的基础上,给出了检验控制系统的各种基准测试、输入约束以及控制目标等,如表1所示[4]。

表1 输出与输入量约束条件Tab.1 Simplified diagram of the production process of Alstom gasifier
2 控制器的设计
由于模型预测控制器是基于模型建立起来的,因此在预测控制器设计之前必须先建立气化炉局部线性化模型。文献[5]给出了子空间辨识模型的方法,在100%典型工况下稳定工作运行状态,对Alstom Simulink环境下的气化炉模型加入如图2(a)~图2(b)所示的伪随机扰动(即系统的输入量),得到如图2(e)~图2(h)所示的系统开环响应曲线。这里随机扰动输入不超过稳态输入的5%,使用子空间辨识即可得到离散状态空间模型。
激励与响应曲线如图2所示。
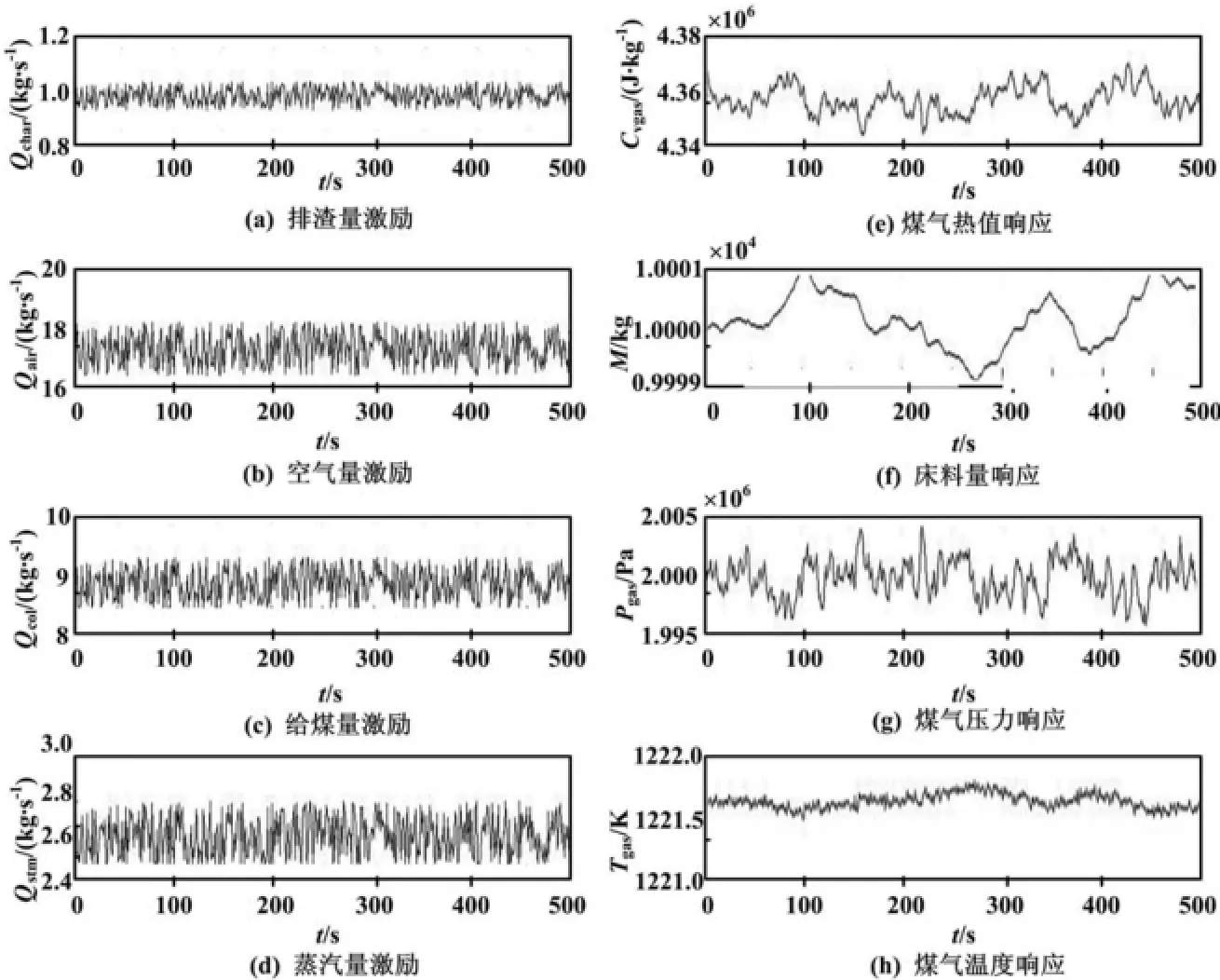
图2 激励与响应曲线Fig.2 The excitation and reponse curves
假设某一工况下,气化炉的动态特性可以用下列离散状态空间表示[6]:
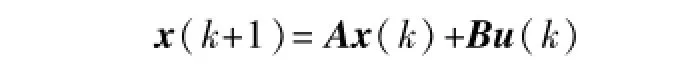
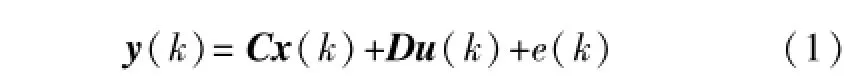
由于在辨识过程中可以使得直通矩阵D为零矩阵,因此状态空间可以表示为:
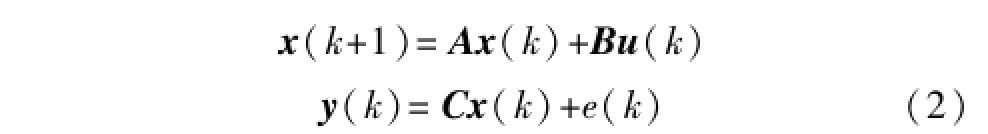
式中:k为第k个采样周期;x∈R25;u∈R4,y∈R4为相对于初始状态的偏移量;e(k)为对象与模型之间的输出偏差;A、B、C分别为系统的状态矩阵、输入矩阵和输出矩阵。
系统初始状态下认为x(0)=0,u(0)=0,y(0)=0。对于e(k)而言,在k时刻认为e(k)=ym(k)-Cx(k),并且有e(0)=0,e(k+i)=e(k)。
以离散状态空间模型为预测模型,预测系统未来的多步输出,假设没有扰动存在,有:
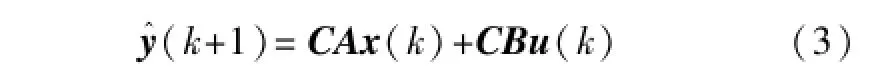
同时为了求出当前的控制增量,可以把u(k)写成u(k)=u(k-1)+Δu(k),从而可以得到:

依次迭代可以得到:
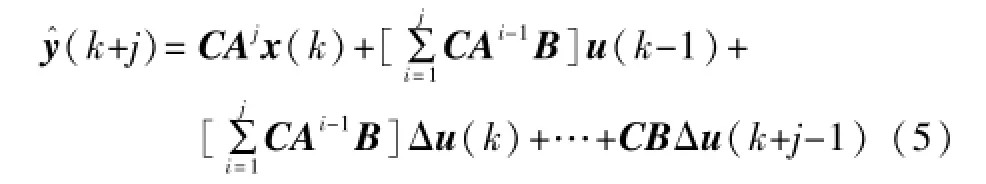
假设预测时域为P,控制时域为M,写成矩阵形式可以得到:
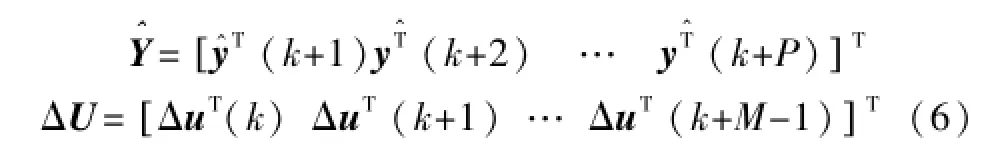
系数矩阵分别为:
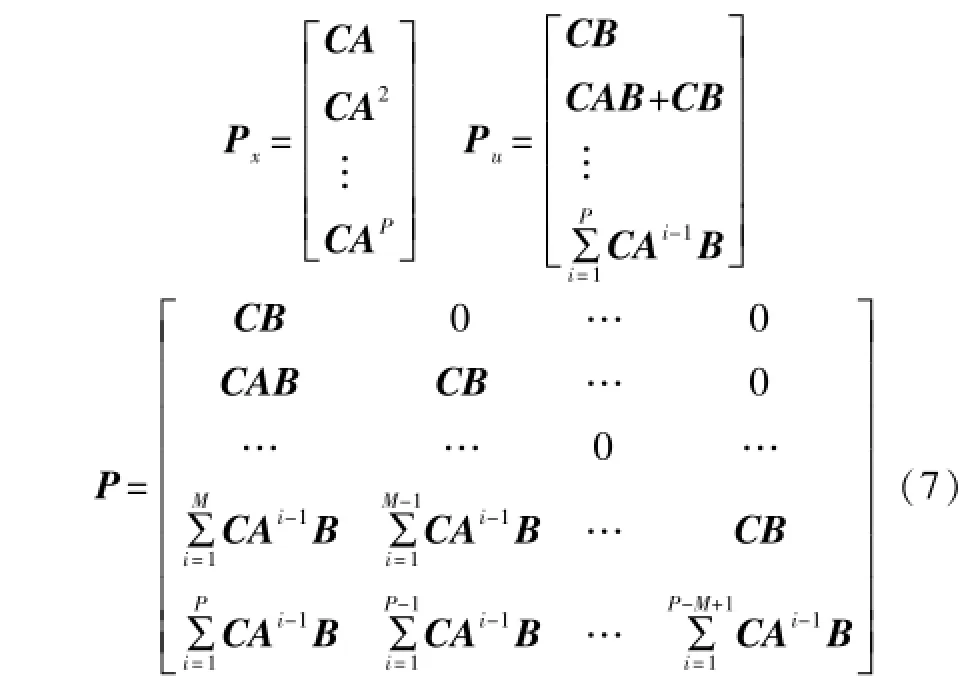
因此可以得到:
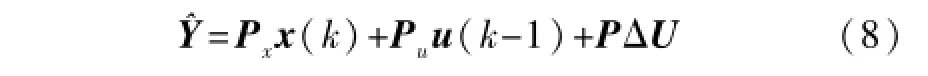
一般而言,要用k时刻的模型误差来进行校正,e(k)=y(k)-(k),其中y(k)为实测值,(k)为模型预测值,因此可以把式(8)写成:
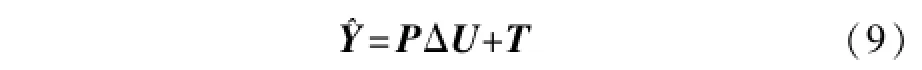
式中:T=Pxx(k)+Puu(k-1)+Ie(k)。

由表1和表2可知,气化炉的控制要受各种约束条件的限制,因此无约束情况下得到的控制输入量往往不能满足实际的控制需求。
根据基准测试要求,有以下输入速率约束与输入幅值受限。这是一个QP问题,可以通过积极集法来求解[7]。

3 灰色预测误差校正器设计
在上述预测控制器的设计中,实测值与模型的输出误差(模型的不匹配)只能知道当前k时刻误差e(k),在未来的P步预测时域内,误差e是未知的。在处理过程中,往往把k时刻的误差e(k)当做未来时刻的误差来进行校正,反馈校正的效果有限。实际上,过往的误差序列含有相当的先验知识[8],所以引入灰色预测理论,对预测时域内的误差进行多步预测,采用等维信息GM(1,1)模型。下面假设以床料量M输出量通道y1为例,设计误差校正器。设定通道y1的通道误差序列为:
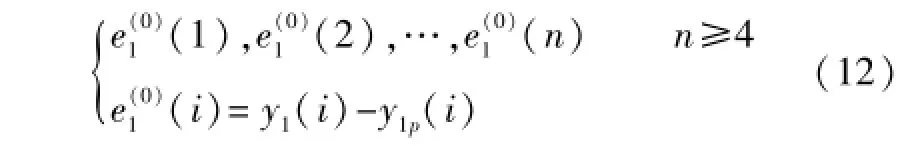
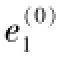
对误差序列进行一次累加,可以得到累加误差序列:
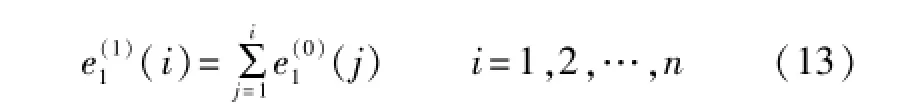
利用式(13)建立灰微分方程:
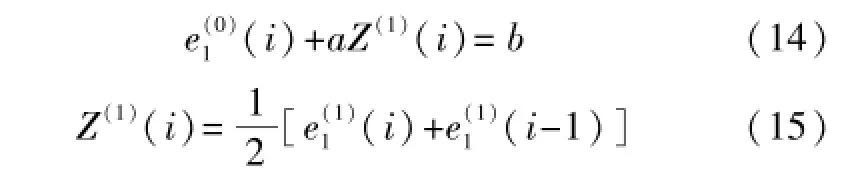
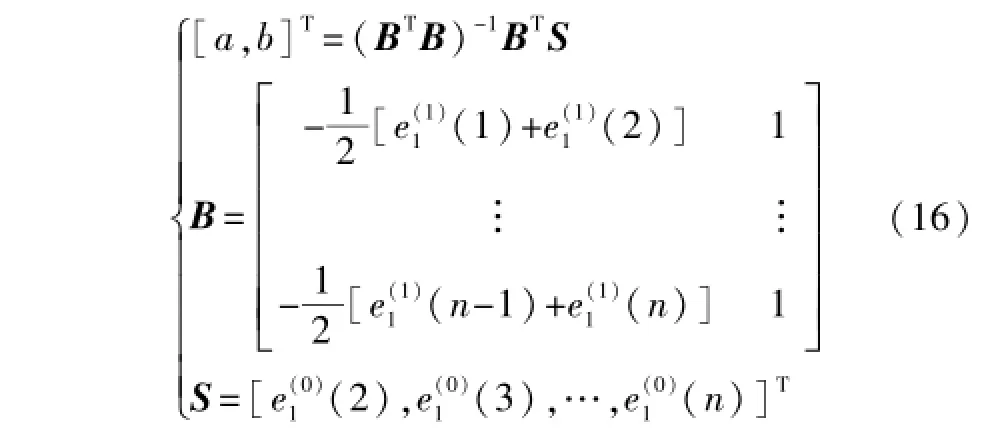
白化方程可以很容易得到解析解,如式(17)所示。
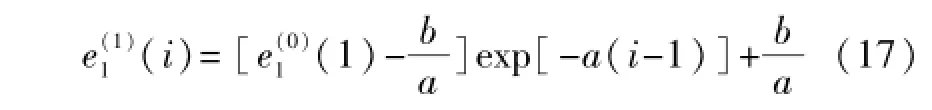
该解析解是累加误差的解析解,因此进行还原计算,最终得到:
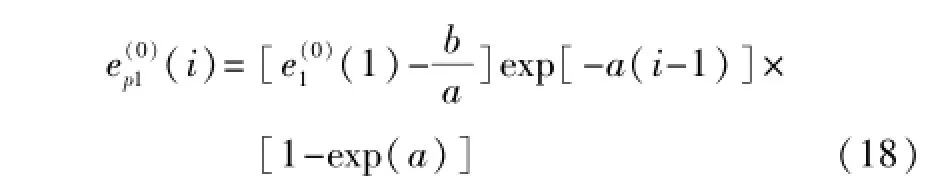
式中:i=1,2,…,n+P。
在k时刻进行预测控制器误差校正时,可以得到:

4 仿真结果
本文在Matlab Simulink环境下对所设计的控制器进行仿真,并验证所设计的控制器是否能满足Alstom能源中心所提出的约束性条件[10]。经过调试后,各个参数的选择如下:预测时域P=20,控制时域M=8,采样时间Ts=1 s,输入权矩阵Q=diag(Q0,Q0,…,Q0),R= diag(R0,R0,…,R0),Q0=diag(2,2e2,2,2e6),R0= diag(1e5,5e3,5e3,1e4)。
鉴于篇幅,这里只给出100%典型工况下的测试曲线,按照基准测试要求,分别进行以下吸入口压力扰动测试。
在系统稳定运行3 000 s后,气化炉下游吸入口压力加入-2 bar的阶跃扰动,在控制器作用下运行500 s,则吸入口压力加入-2 bar阶跃扰动后的负荷变化曲线如图3所示,输入输出变化曲线如图4所示。
在系统稳定运行3 000 s后,气化炉下游吸入口压力加入幅值为2 bar、频率为0.04 Hz的正弦扰动,仿真500 s,输入输出变化曲线如图5所示,这里略去了负荷变化曲线。
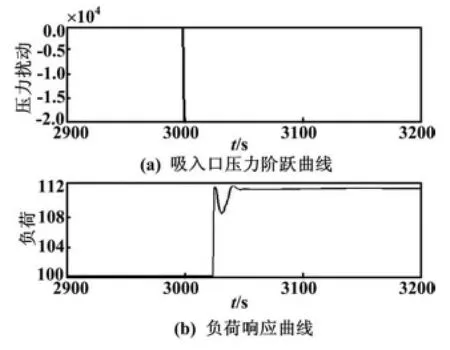
图3 吸入口压力阶跃扰动及负荷响应曲线Fig.3 Suction inlet pressure step disturbance and load response

图4 吸入口压力阶跃扰动测试仿真曲线Fig.4 Simulation test curves of suction inlet pressure step disturbance curves
另外,给出了在控制过程中输入输出量变化的最大值以及变化速率,如表2所示。
从表2可以看出,在100%典型工况下,该预测控制器能够很好地满足Alstom能源技术中心所提出的气化炉控制基准问题,可见该预测控制器具有一定的理论意义。

图5 吸入口压力正弦扰动测试仿真曲线Fig.5 Simulation test curve of suction inlet pressure sinusoidal disturbance

表2 100%典型工况下加扰动测试结果Tab.2 Disturbance test result under 100%typical operation condition
5 结束语
在Alstom能源技术中心给出的气化炉模型基础上,基于状态空间模型的预测理论设计集中化的控制器,并且在预测校正环节加入了灰色预测。该方法基于当前时刻以及以往时刻由于模型不匹配产生的误差先验序列进行未来的误差预测,并用于预测控制器的设计当中。在推导出控制规则后,在Matlab Simulink环境下通过s-function函数编写控制器模块并封装加入气化炉模块当中,在扰动测试中得到了符合基准测试下的控制效果。仿真结果产生曲线以及数据证明该方法具有较好的控制效果,因此具有一定的理论意义。
[1] 姚秀平.燃气轮机及其联合循环发电[M].北京:中国电力出版社,2004.
[2] 钱积新,赵均,徐祖华.预测控制[M].北京:化学工业出版社,2007.
[3] 薛亚丽,李东海,王军.Alstom气化炉基准问题的控制特性分析[J].清华大学学报:自然科学版,2009,49(5):80-85.
[4] Dixon R,Pike A.Introduction to the 2nd Alstom benchmark challenge on gasifier control[C]∥Control 2004.Bath,UK,2004:585-601.
[5] 吴科.联产系统煤气化过程的建模和控制研究[D].南京:东南大学,2010.
[6] Seyab R K A,Cao Y.Nonlinear model predictive control for the Alstom gasifier[J].Journal of Process Control,2006,16(8):795-808.
[7] 岳俊红.复杂工业过程多模型预测控制策略及其应用研究[D].北京:华北电力大学,2008.
[8] 郭鹏,师东娜.灰色误差校正多变量动态矩阵控制[J].电机与控制学报,2008,12(2):223-227.
[9] 杨华龙,刘金霞,郑斌.灰色预测GM(1,1)模型的改进及应用[J].数学的实践与认识,2011,41(23):39-46.
[10] 李东海,王军,薛亚丽.Alstom气化炉的适应性非线性控制[J].清华大学学报:自然科学版,2009,49(2):265-268.
Improved Predictive Control for Alstom Gasifier
Alstom Energy Technology Center has given the Matlab nonlinear model for gasifier under full operating condition.In order to solve the control problem caused by the non-linearity,tight coupling and large inertia of the gasifier from Alstom,the model predictive controller has been designed.Firstly,the off line linear model is set up under some of the local operating conditions,then on the basis of the model established,the controller is designed.By adopting grey theory GM(1,1),in the error correction stage,the error that generated due to model mismatch in future is predicted,thus the accuracy of controller output is enhanced.The simulation results indicate that in pressure disturbance tests,even control variables are given strict constraints,the deviation of each variable still keeps within a predetermined range;this satisfies the control requirements for Alstom gasifier.
Alstom gasifier Non-linear system Offline modeling Model predictive control Grey theory prediction error correction
TP323
A
国家863基金资助项目(编号:2006AA05114-2)。
修改稿收到日期:2014-02-14。
杨小龙(1989-),男,现为东南大学动力工程及工程热物理专业在读硕士研究生;主要从事热工自动控制方向的研究。

