象山港海域海洋环境监测站位优化及验证分析
曹 维,仵彦卿,唐德富,杨耀芳,沈继平,费岳军
(1.国家海洋局 宁波海洋环境监测中心站,浙江 宁波 315012;2.上海交通大学 环境科学与工程学院,上海 200240)
0 引言
象山港位于宁波市东南部,穿山半岛与象山半岛之间,东临大目洋,是一个由东北向西南深入内陆的狭长型半封闭海湾,全港纵深60km,水深为10~15 m,港湾内有西沪港、黄墩港和铁港3个支港。象山港属内陆海港,为半封闭型海湾,尽管有潮汐的作用,但其海水交换能力差,不利于污染物的降解和扩散,环境容量较小[1]。
20世纪70年代初期,宁波市卫生防疫站负责象山港水质监测任务[2];1976年起,宁波市环境监测中心站承担了象山港水质监测任务,设置了5个站位(吉奇、黄墩港、下山、黄避岙和野龙山);1983年和1985年在上述5个站位增测了沉积物样品;2002年,国家海洋局在象山港海域设置了赤潮监控区[3]。受监测能力和监测经费的影响,象山港监测站位数量有限,站位分布也不具代表性。随着我国对海洋环境保护工作的重视,港湾海域监测工作有待进一步规范和深化,因此,有必要对监测站位进行优化。本研究利用2011年度海洋环境评价项目《象山港海域海洋环境质量综合评价方法 DOMEP(MEA)-03-02》专题调查监测数据,结合同期赤潮监控区和趋势性监测资料①,进行站位优化和验证分析,希望通过优化后的监测站位全面掌握港湾环境质量,更好地为海洋环境保护管理提供决策依据。
1 站位优化方法
目前关于监测站位优化的新方法,主要有物元分析法[4]、灰色局势决策分析法[5]、序贯数论法[6]、模糊优选法[7]、密切值法[8]、模糊聚类法[9]和人工神经网络优选法[10]等,但上述方法在一定程度上存在缺陷。
克立金方法(Kriging)[11]是 G.Matheron教授以南非矿山地质工程师D.G.Krige的名字命名的一种方法。从数学上讲,克立金法是一种对空间分布数据
①宁波市海洋与渔业局.2011年宁波市海洋与渔业环境监测成果汇编(内部资料)[G].宁波:宁波市海洋与渔业局,2012.求最优、线性、无偏内插估计量的方法。从海洋环境研究角度讲,它是根据已知监测站位点上的环境要素变量,如某种污染物浓度的实测数据,对环境要素变量进行结构性分析(变差函数模型的确定)之后,为了对待估点作出一种线性、无偏、最小方差的估计,而对周围已知站位点的测量值赋予一定权系数,进行加权平均来估计待估点环境要素变量的方法。
本次站位优化设计运用普通Kriging方差分析法,采用下式计算研究区海洋环境要素的估计误差标准差,同时结合研究区污染现状,进行海洋环境监测站位优化分析:
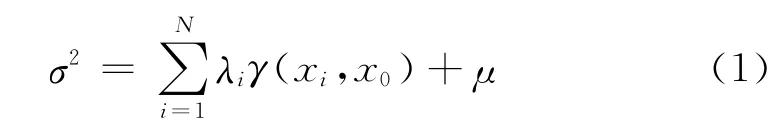
式中:σ为估计误差的标准差;λi(i=1,2,...,N)为克立金权系数;N为已知监测点总数;μ是拉格朗日乘子;xi=(xi,yi),为已知监测i点的坐标;x0=(x0,y0),为待插值点的坐标;γ(xi,x0)=γ(h)为变差函数,h为(x0,y0)到(xi,yi)之间的距离矢量,于是,γ(h)可用下列公式计算:
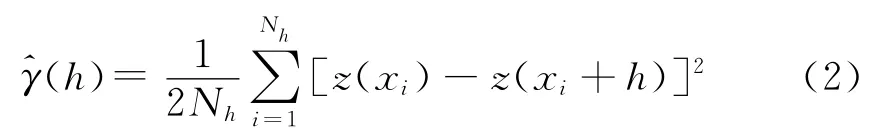
求得变差函数后,代入下式可以计算权系数λi(i=1,2,...,N)和拉格朗日乘子μ:
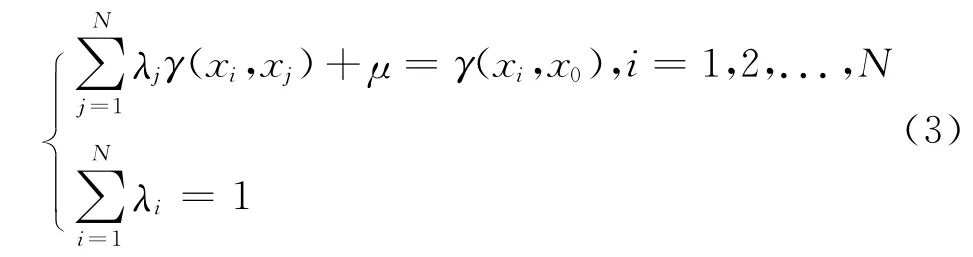
将式(3)求得λi(i=1,2,...,N)和μ代入到式(1),可以得到所有未知点的方差值。该方差的大小可反映已有监测站位质量的优劣。
利用方差减少法,进行现有监测站位的优化分析,站位优化调整的原则为:
(1)污染物扩散浓度梯度大的区域,加大监测站位密度,否则,减少站位密度;
(2)考虑到海洋水动力条件,在流速梯度大的区域,加大监测站位密度,否则,减少站位密度;
(3)污染源分布的地区,需要加密站位;
(4)对于有长序列的站位,尽可能保留;
(5)对海洋近岸地区,加大站位密度,远海区域减少站位密度;
(6)监测站位优化是一个过程,与经费投入和环境信息提取精度有关,因此,在站位优化时,还要考虑目前的海洋环境研究状况和经费投入。
2 站位优化实例
2.1 数据来源
研究采用的水质、沉积物质量、生物生态数据主要来源于2011年度海洋环境评价项目专题监测数据,结合同期象山港赤潮监控区和趋势性监测数据;水文(水温和盐度)、沉积物类型采用2011年度海洋环境评价项目专题调查数据。
2.2 现有监测站位
象山港现有13个赤潮监控区站位、6个趋势性监测站位、31个专题调查站位(港口7个、港中11个、港底13个),共有50个监测站位(图1)。
2.3 站位优化结果
根据普通Kriging方差分析法,计算得到象山港现有监测站位水质要素估计误差标准差平均值为0.190(图2),湾底和湾中部的估计误差标准差较小,而在湾口区域的估计误差标准差较大。此外,在观测点较密的区域,估计误差标准差小;反之,估计误差标准差大。
同时,通过象山港海域水质各监测要素值的标准化和归一化处理,进行现有水质污染状况分析。考虑到不同时期数据的差异性,采用31个专题调查站位的水质监测数据进行水质污染状况分析(图3)。可以得出,象山港湾底污染程度较严重,湾中部区域次严重,湾口区域较轻。
结合象山港现有监测站位水质估计误差标准差和象山港现有水质监测污染程度(图2和图3),对象山港水质监测站位进行优化。优化后象山港有38个水质测点(图4),删减了12个近岸站点,优化后的水质要素平均估计误差标准差为0.168(图5),增加了11.6%,删减的监测站位包括5个赤潮监测站位(XS05、XS07、XS08、XS09和XS12)、2个趋势性监测站位(D33ZQ037和D33ZQ038)以及5个专题调查站监测站位(QS2、QS6、QS10、QS22和 QS27)。
水质站位设置:根据象山港丰水期和枯水期水体中各类污染物分布特点(图6),充分考虑能监测各类污染物重点分布区域,同时统筹考虑象山港水团(图7)和水动力[12](图8)分布区域,优化后得到38个水质监测站位(图4)。
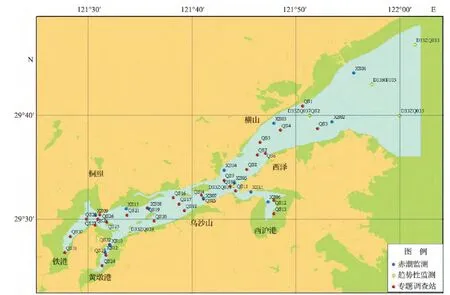
图1 象山港现有监测站位Fig.1 Present monitoring stations in Xiangshangang Bay
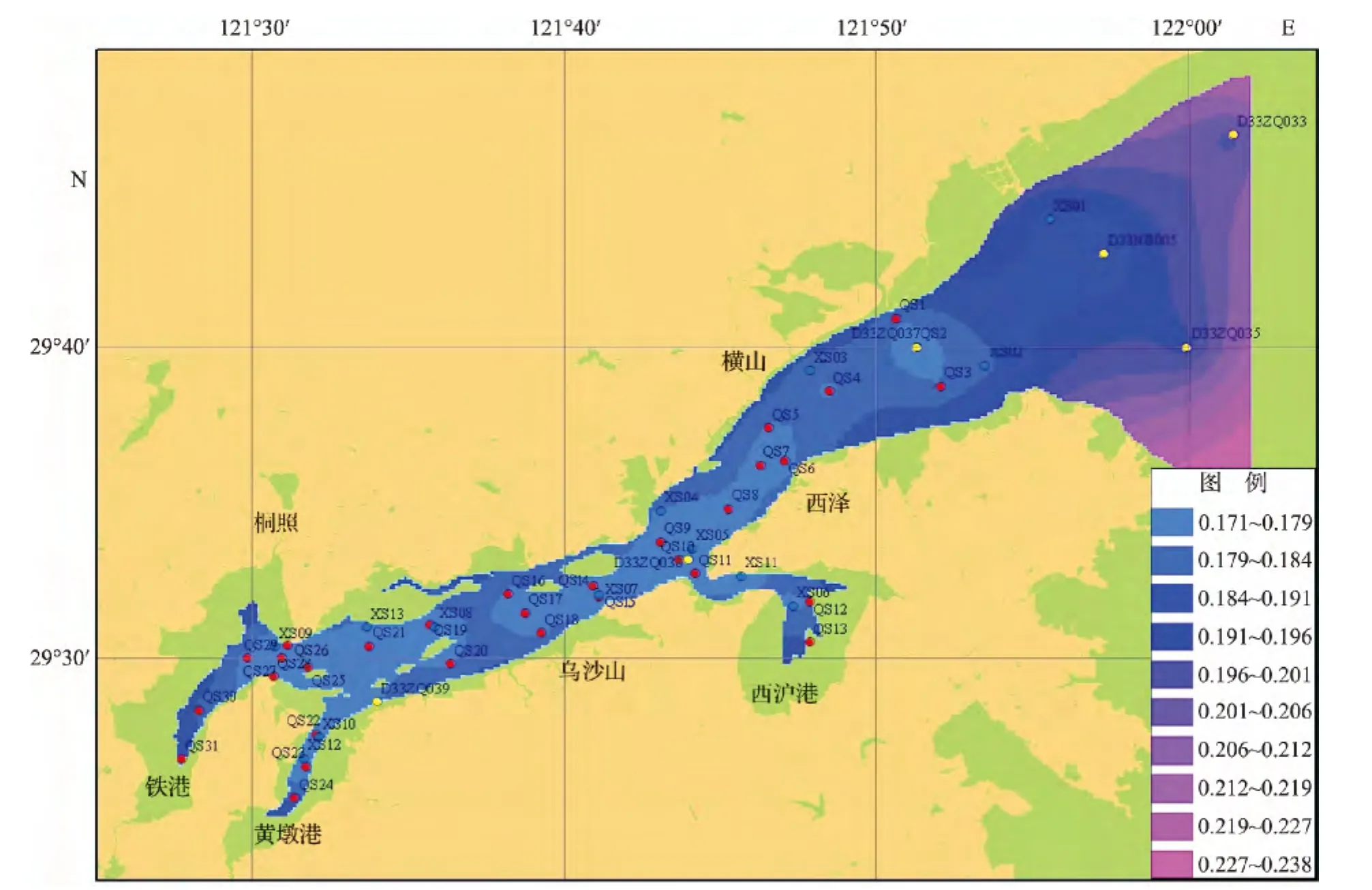
图2 现有站位水质估计误差标准差Fig.2 Water quality estimated standard deviation of present stations
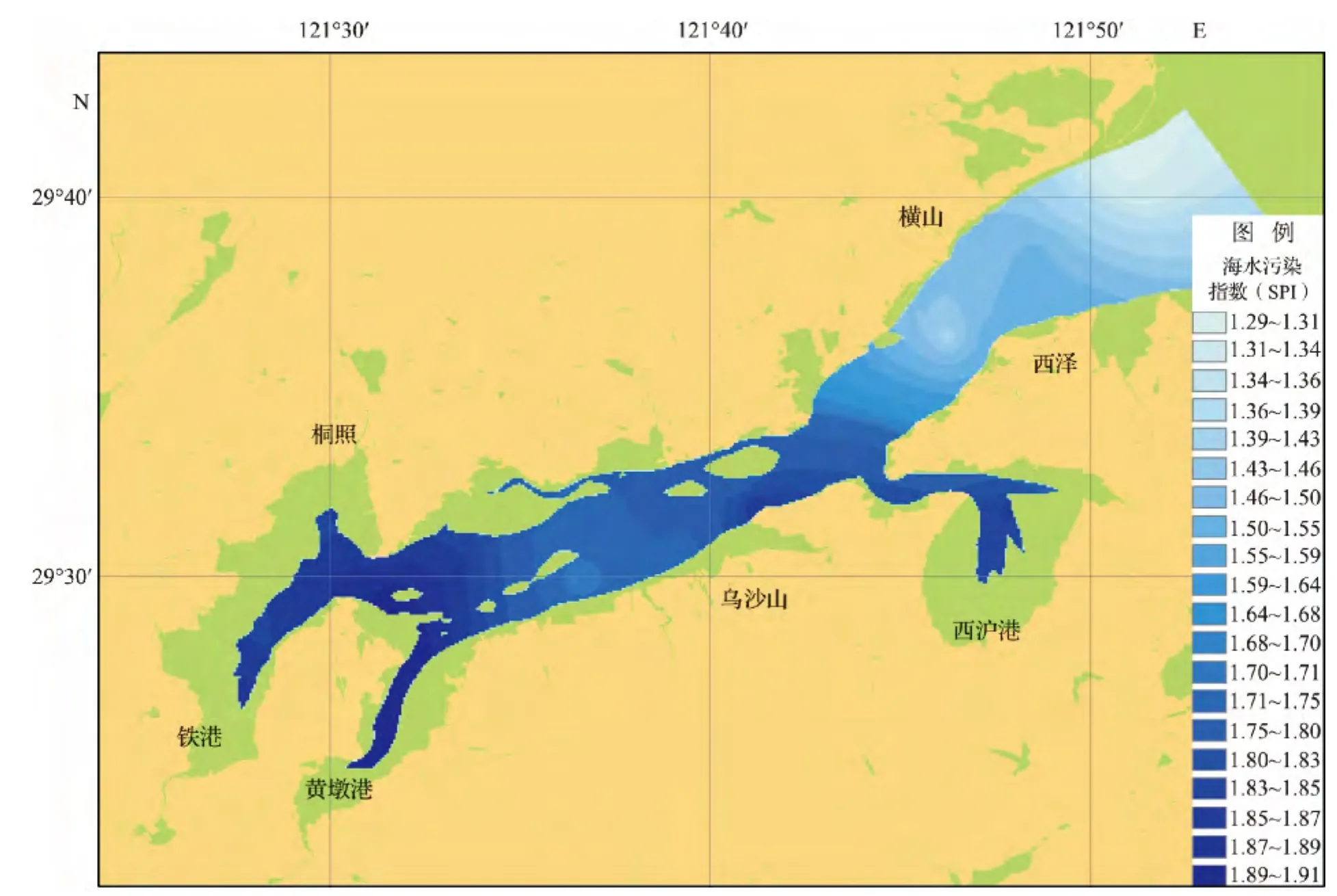
图3 现有水质污染状况Fig.3 Present pollution condition of water quality
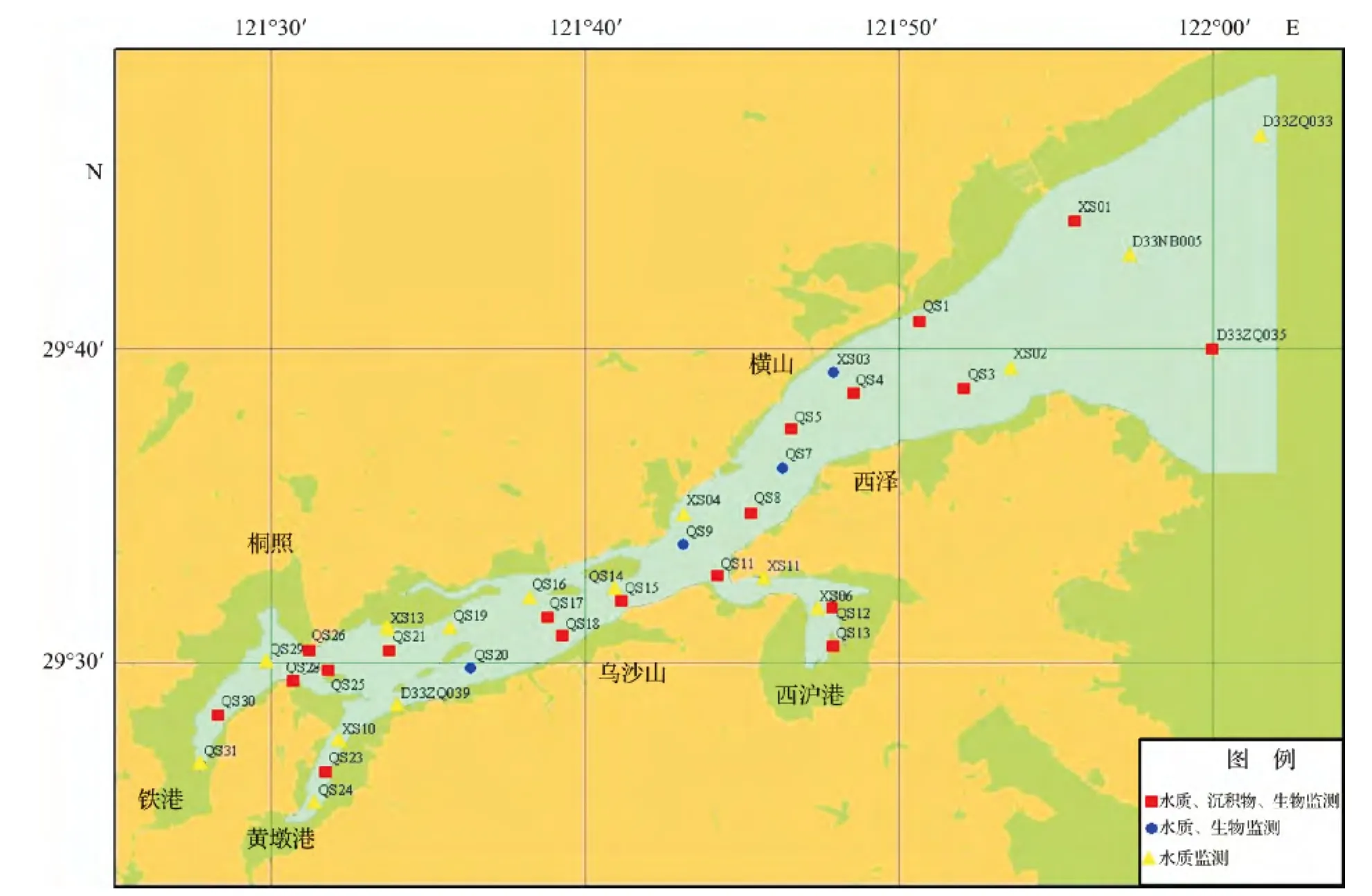
图4 优化后的监测站位Fig.4 Optimized monitoring stations
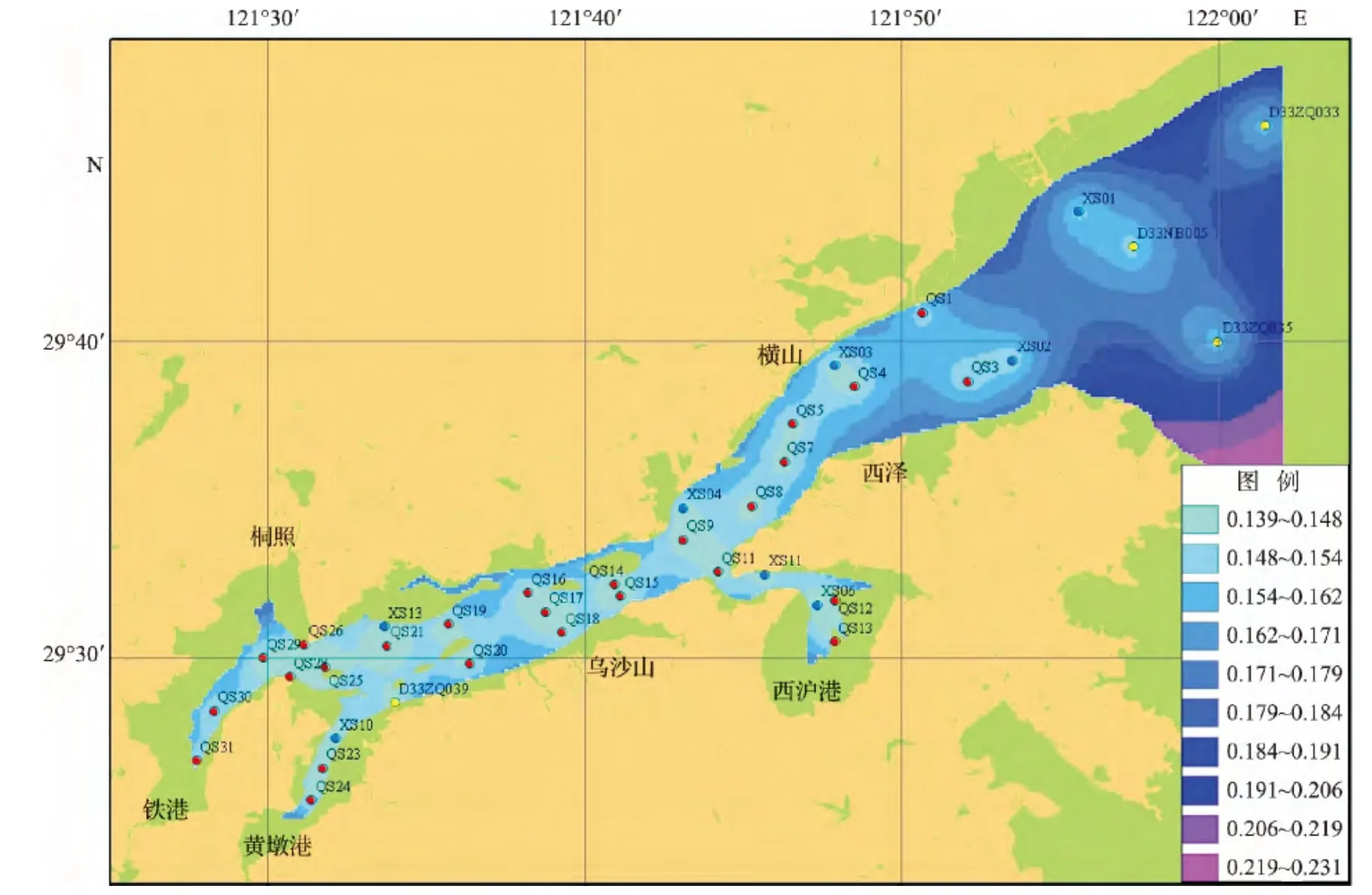
图5 优化站位水质估计误差标准差Fig.5 Water quality estimated standard deviation of optimized stations
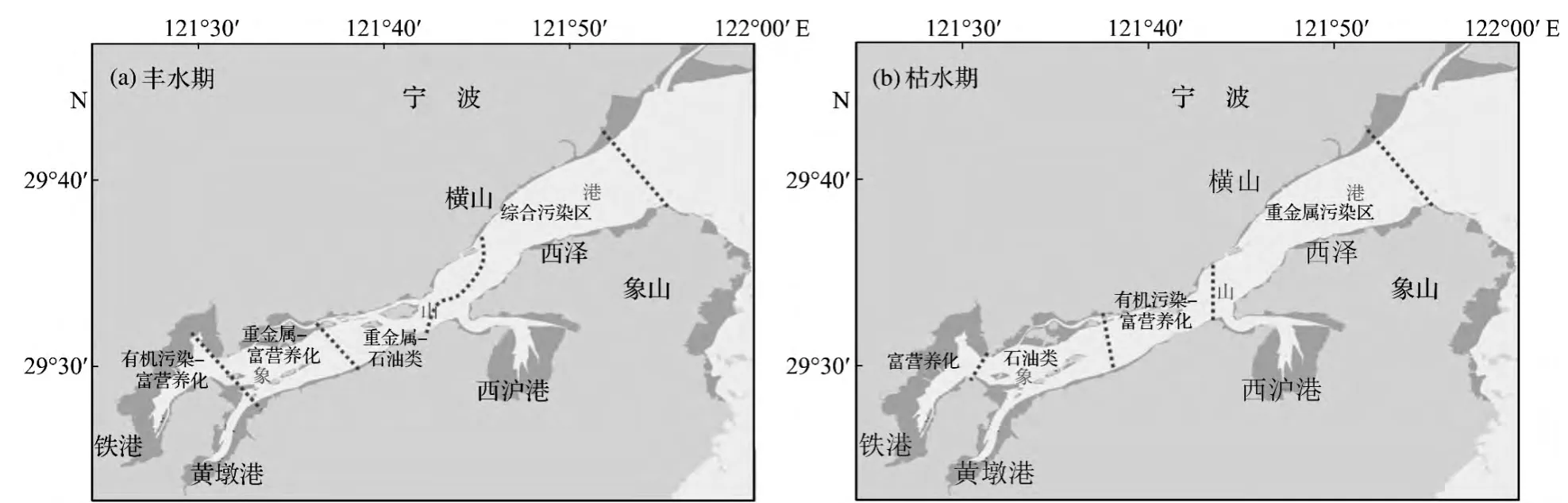
图6 水质污染物分布Fig.6 Water pollutant distribution
图7 水团分布Fig.7 Water mass distribution
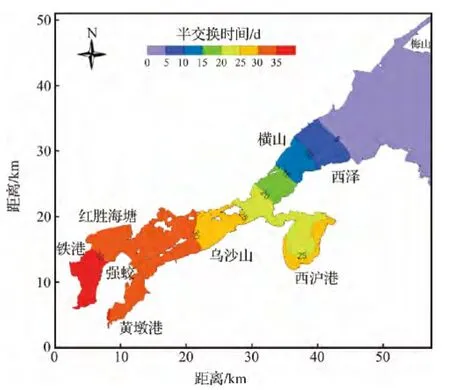
图8 水体半交换时间Fig.8 Half exchange time of water
沉积物站位设置:原则上沉积物站位数为优化后水质监测站位数的50%,合理布局,均匀分布。同时,充分考虑布点覆盖所有沉积物类型(图9),且各沉积物类型上设点密度基本保持一致,尤其是狮子口北面的QS26号站位因其仅有的贝壳-砂沉积物类型,故予以保留。对于有长序列的站位,尽可能保留,在站位设置中保留了具有多年沉积物监测数据的趋势性监测站位(D33ZQ035)。优化后共得到19个沉积物监测站位(图4)。
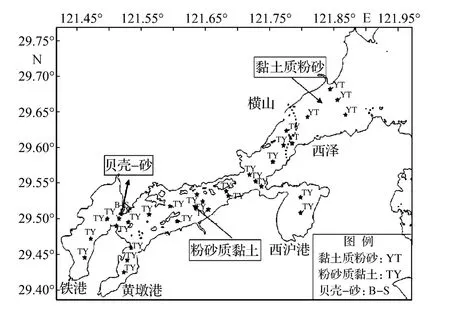
图9 沉积物类型分布Fig.9 Distribution of sediment types
生物生态站位设置:充分考虑象山港水团分布特征,浮游生物和底栖生物的群落分布特征,使站位覆盖各类型水团和各生物群落类型。根据水质优化站位来看,已覆盖所有类型的水团和浮游生物、底栖生物群落,生物生态站位数在取60%水质站位数的过程中,做到均匀、有序地删减。根据浮游植物优势种类的生态类型和分布特点,将象山港浮游植物进行生态类型划分。夏季象山港可划分为沿岸种分布区、近岸温带种分布区和半咸水种分布区3个主分布区,在狮子口海域有少量热带种出现(图10a)。冬季象山港可分为外洋广温种分布区、近岸暖海种分布区、广温广布种分布区和半咸水种分布区4个区域(图10b)。底栖生物站位应充分考虑布点覆盖所有沉积物类型,且各沉积物类型上设点密度基本保持一致,根据此原则,在狮子口北面的贝壳-砂沉积物类型中,保留QS26号站位,以充分覆盖和均匀分布各底质类型。为了尽可能保留长序列的站位,在站位设置中保留了具有多年生物监测数据的趋势性监测站位(D33ZQ035)。优化后共为23个生物生态监测站位(图4)。
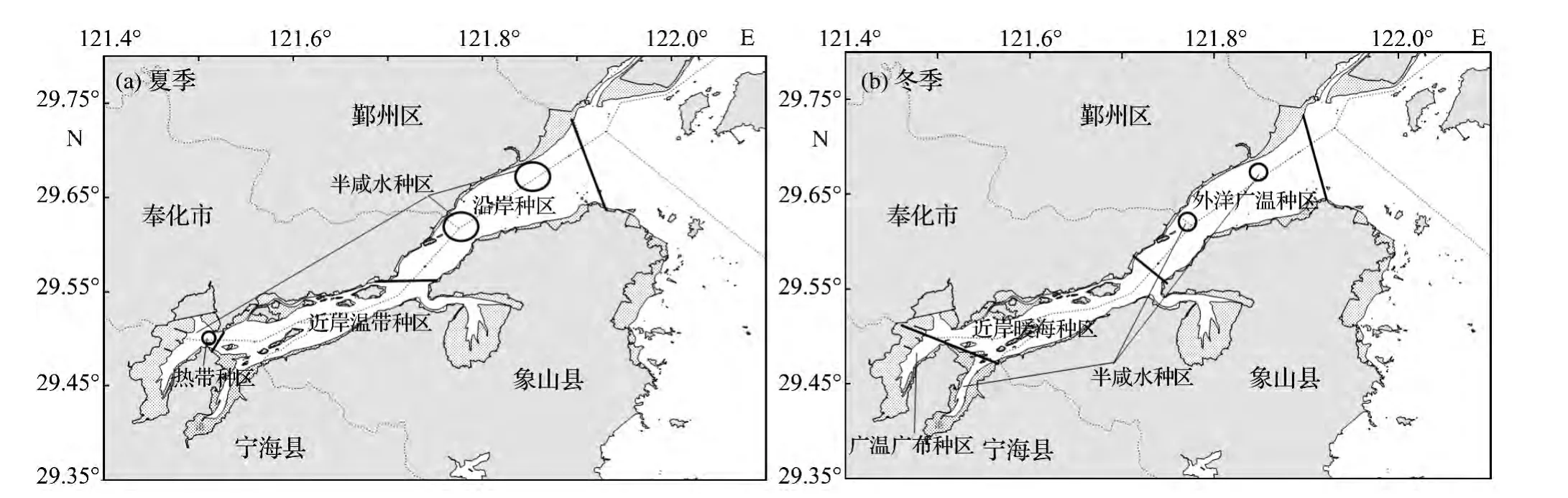
图10 浮游植物类型分布Fig.10 Distribution of phytoplankton communities
3 验证分析
为了验证优化后监测站位所反映的生态环境质量与现有监测站位所反映的生态环境质量之间是否存在差异,需对2组数据进行显著性检验。在数理统计中一般以概率(P)0.05作为显著评定标准,即在100次试验中,由于偶然因素造成差异的可能性在5次以上,其差异被认为是不显著。如果两者差异在概率为5%的范围内,出现这样概率的机会非常小而出现了,那么我们就认为此差数具有显著差异程度。
根据2011年象山港生态环境专题调查结果,结合同年在象山港开展的赤潮监控区、趋势性监测等相关资料,采用统计学中的T检验方法,对站位优化前、后象山港海域的水质、沉积物和生物生态监测数据进行显著性检验。其中,水质采用溶解氧、化学需氧量、活性磷酸盐、无机氮、石油类、重金属(汞、砷、铜、铅、锌、镉、铬)等12个指标的监测值;沉积物采用石油类、滴滴涕、多氯联苯、重金属(汞、砷、铜、铅、锌、镉、铬)等10个指标的监测数据;生物生态采用浮游植物、浮游动物和底栖生物的多样性指数。经统计检验(表1),站位优化前、后的2组数据之间无显著性差异,说明优化后的监测站位(38个水质站位、19个沉积物站位、23个生物生态站位)所表征的监测信息量与现有50个监测站位的信息量等效,可作为今后的常规监测站位。
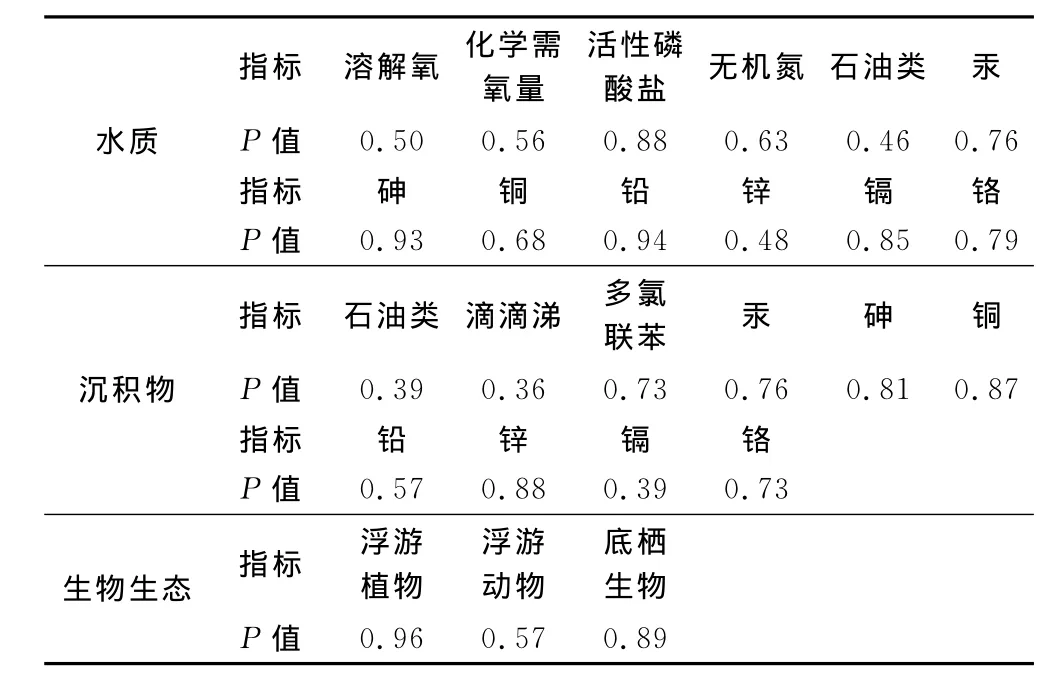
表1 站位优化前、后监测数据显著性检验Tab.1 Significant testing of original and optimized monitoring data
4 小结
根据2011年象山港海域生态环境监测资料,运用普通Kriging方差分析法进行海洋环境监测站位优化,再采用统计学中的T检验方法,对站位优化前、后象山港海域生态监测数据进行方差分析,经统计检验,2组数据之间无显著性差异,说明优化后的38个监测站位能较好地代表象山港海域的生态环境质量,其所表征的监测信息量与现有50个监测站位的信息量等效,故可作为今后的常规监测站位。
(References):
[1]LI Nai-fang,LI Ying-bao.Discussion on resource characteristics and development mode of Xiangshan port[J].Ningbo Teachers College:Social Science Edition,1986(4):101-104.
李乃芳,李英保.试论象山港的资源特征和开发方式[J].宁波师范学院:社会科学版,1986(4):101-104.
[2]HU Wen-xiang,CHEN Tie-rong,XIN Ying,et al.The assessment on the environment monitoring of XiangSanPort[J].Marine Environmental Science,1995,14(4):57-63.
胡文翔,陈铁熔,忻颖,等.象山港环境监测总结评价[J].海洋环境科学,1995,14(4):57-63.
[3]ZHANG Li-xu,JIANG Xiao-shan,CAI Yan-hong.Variations on nutrients and the characteristic of their structure in the red tidemonitoring area of Xiangshan Habor in recent four years[J].Marine Sciences Bulletin,2006,25(6):1-9.
张丽旭,蒋晓山,蔡燕红.近4年来象山港赤潮监控区营养盐变化及其结构特征[J].海洋通报,2006,25(6):1-9.
[4]GAO Ming-hui.Reseach on optimized selection in water quality environmental monitoring by substance elemant analysis[J].Environmental Science and Technology,1997,20(4):26-27.
高明慧.物元分析用于水质环境监测优化布点的研究[J].环境科学与技术,1997,20(4):26-27.
[5]ZHANG Yong,HUANG Xing-qun,YI Zhi-wei,et al.Optimized selection in river monitoring points by grey situation substance elemant analysis[J].Environmental Monitoring in China,1996,15(3):24-26.
张勇,黄醒群,易志伟,等.灰色局势物元分析进行河流优化布点[J].中国环境监测,1996,15(3):24-26.
[6]LI Feng,LI Yong-gan.Optimized selection in river monitoring sites by sequential number-theoretic optimization method and silhouette graph[J].Environmental Monitoring in China,2000,16(4):15-17.
李峰,李永干.序贯数论优化法和侧影图进行河流优化布点[J].中国环境监测,2000,16(4):15-17.
[7]DOU Su-zhen,WANG Li-hong,HOU Cun-dong,et al.A fuzzy optimization model of preferential location in urban air environmental monitoring and case study[J].Ubran Environment & Ubran Ecology,2001,14(5):55-58.
窦素珍,王黎虹,侯存东,等.城市大气环境监测优化布点模糊优选模型及应用实例[J].城市环境与城市生态,2001,14(5):55-58.
[8]XU Li-zhong,ZHANG Jiang-shan.Optimization of atmospheric environmental monitoring sites with modified intimate value method[J].Environmental Engineering,2000,18(2):50-53.
许丽忠,张江山.改进密切值法优化大气环境监测布点[J].环境工程.2000,18(2):50-53.
[9]LIANG Wei-zhen,YE Jin-run,YANG Jing.Optimized selection in water quality monitoring by fuzzy cluster analysis method[J].Environmental Monitoring Management and Technology,2002,14(3):6-7.
梁伟臻,叶锦润,杨静.模糊聚类分析法优化城市河涌水质监测点[J].环境监测管理与技术,2002,14(3):6-7.
[10]LI Zou-yong,XU Ting-ting,DING Jing.Application of artificial neural network to optimize groundwater quality monitoring sites[J].Ubran Environment & Ubran Ecology,2003,16(6):169-171.
李祚泳,徐婷婷,丁晶.地下水环境监测优化布点的人工神经网络模型[J].城市环境与城市生态,2003,16(6):169-171.
[11]KANG Yong-shang,SHEN Jin-song,CHEN Zhuo-heng.Modern mathematics geology[M].Beijing:Petroleum Industry Press,2005:114-131.
康永尚,沈金松,谌卓恒.现代数学地质[M].北京:石油工业出版社,2005:114-131.
[12]PENG Hui,YAO Yan-ming,LIU Lian.Study on the features of water exchange in Xiangshangang Bay[J].Journal of Marine Sciences,2012,30(4):1-12.
彭辉,姚炎明,刘莲.象山港水体交换特征研究[J].海洋学研究,2012,30(4):1-12.

