并行输电线路工频电磁场的叠加算法研究

曹红英 张 翼 白永祥 唐 波 彭友仙

（1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.河南省电力公司 三门峡供电公司，河南 三门峡 210098）

目前随着全球用电量的增加，并行输电线路受到国内外越来越多输电线路设计者的青睐.随之而来的并行线路的电磁环境问题也受到更多的关注.我国是一个能源分布不均衡的国家，一次能源的存储主要集中在经济相对落后的区域，而这些区域的用电负荷相对较少，这就促使国家采取措施对电力资源进行合理的利用，其中西电东送、南北互供的方法在很大程度上解决了这一问题，但是这也使得我国的输电线路大部分采用了并行和交叉的方式，采用这种方式下的输电线路的电磁环境相对比较复杂［1-4］.

根据我国环保总局对超高压送变电工程中所产生的电磁辐射环境影响的规定，我国将居民区内的工频电场评价标准暂定为4kV／m，将磁感应强度的评价标准暂定为0.1mT.目前主要是以单行输电线路为基础来研究工频电磁场，其值要符合国家对工频电磁场的要求，对于并行输电线路工频电磁场的极大值仍要满足国家规定，故本文对并行输电线路进行研究.

对于并行方式运行的线路，文献［5］提出以有限元为原理进行计算电场强度，但该方法对于所占空间数百米的线路来说，理论方法复杂，计算量极大，在工程应用中存在局限性.对于并行方式运行的线路，亦可采用有限差分的原理进行计算，但是该方法在边界复杂的情况下精度不高.本文以等效电荷为原理，以三峡大学南苑的并行线路为例，对并行输电线路的工频电磁场进行了研究.本文提出了矢量叠加原理的算法，运用此算法对三峡大学南苑输电线路的工频电场强度和工频磁场强度进行计算，并对现场进行实际测量，将两者所得结果进行比较，验证了算法的正确性.

1 并行线路工频电磁场的求解方法

1.1 并行输电线路工频电场的求解方法

1.1.1 传统工频电场的求解方法

等效电荷法［6］：由于在实际工程计算中，束缚电荷在介质分界面上连续分布，而自由电荷也在导体表面上连续分布，但是目前对于这两种电荷的具体分布情况是未知的，不能直接由给定的边界条件解出.如果在计算的场域之外将这些待求的连续分布的电荷用n个被称为模拟电荷的离散电荷来代替，根据等值替代中前后边界条件不变的原则来对各模拟电荷的量值进行求解，这就使得场域内任意一点的电位与场强均可由各模拟电荷所产生的场量（φ，E）叠加而获得，并将此值作为原场的逼近解.

静电场的数学模型可以归结为以电位函数φ为待求量的泊松方程或拉普拉斯方程的定解问题［7-8］.

基本电位方程为

电位系数可表示为

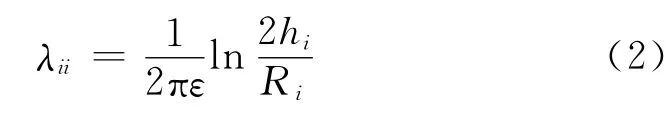
式中，ε为空气介电常数；Ri为输电导线半径.

由此得到相应的电位系数矩阵［p］，由输电线路的电压等级可以得到电压矩阵［U］.多导线线路中单位导线上的等效电荷［Q］主要与电压［U］和麦克斯韦电位系数［p］有关，即

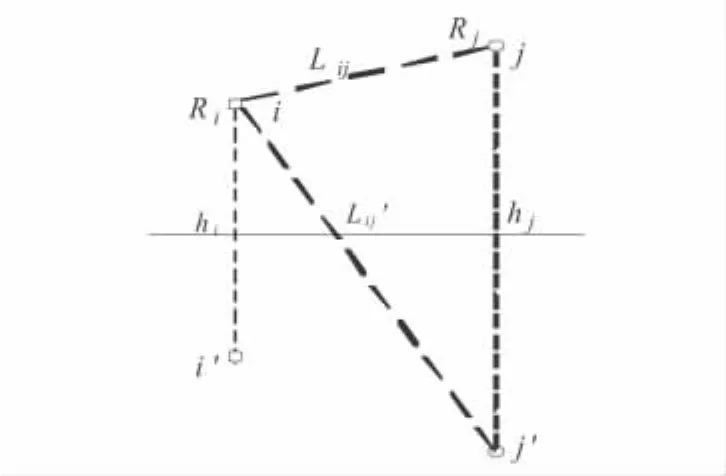
图1 电位系数矩阵示意图

对于三相交流线路，空间中任一点的电场强度如图2所示，可根据叠加原理计算得出，在（x，y）点处的电场强度分量：

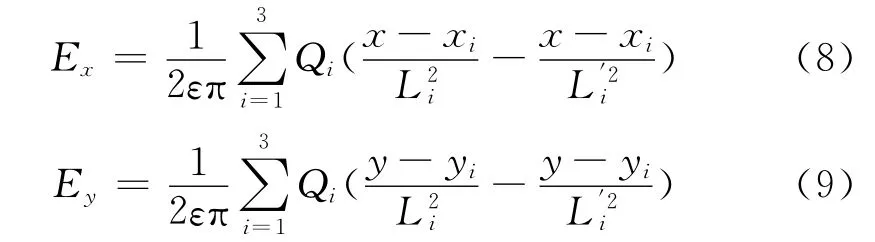
式中，ε为空气介电常数；Qi为等效电荷；m为导线数；xi、yi分别为导线的横纵坐标；Li、分别为导线及其镜像到计算点的距离.

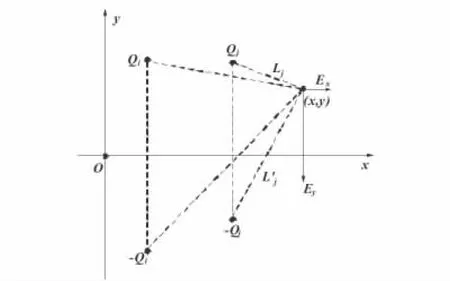
图2 求空间场强的示意图

1.1.2 并行输电线路工频电场的求解方法

按照等效电荷法原理，并行输电线路的计算分两个步骤：1）由输电线路的电压和电位系数矩阵，计算单位长度导线上的电荷；2）计算由这些电荷产生的电场.

计算出线路各相导线所产生的空间电场强度，并分别在平行于地面和垂直于地面进行投影，从而可采用矢量叠加进行并行线路的空间电场的计算；并行输电线路的电场强度模型为

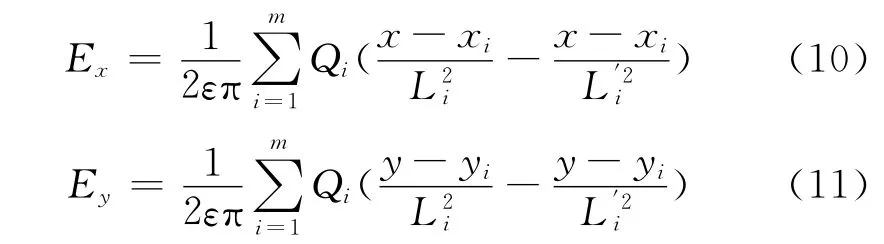
式中，m为导线数；xi、yi分别为导线的横纵坐标；Li、分别为导线及其镜像到计算点的距离.

在并行输电线路中，电压作为一个时间变量，在计算时通常要用复数来表示各相导线的电压，相应的电荷也是复数来表示.

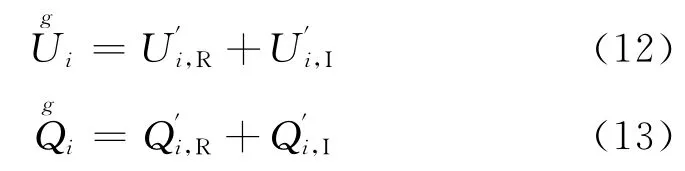
所得电场强度的分量是复数，即

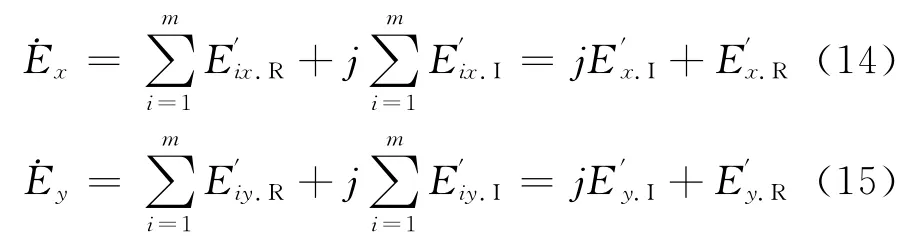
空间中该点的合成场强为

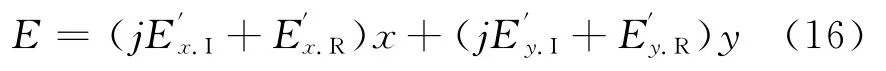
1.2 并行输电线路工频磁场的求解方法

1.2.1 传统工频磁场的求解方法

线路的磁场可以看作仅由电流产生，按照安培环路定理在载流导体中运用即可得到磁场强度.在计算时忽略它的镜像对结果的影响，所得到的计算值与实际值相差不大，故工频磁场强度可用以下公式计算：

磁感应强度B和磁场强度H 存在的关系：

式中，空气磁导率为μ；故可只研究磁场强度H.

对于单根导线磁场强度的求解，空间中任意一点的坐标为（x，y），导线的坐标为（xi，yi），通过导线的电流为I，则求解空间任一点的磁场强度的公式为

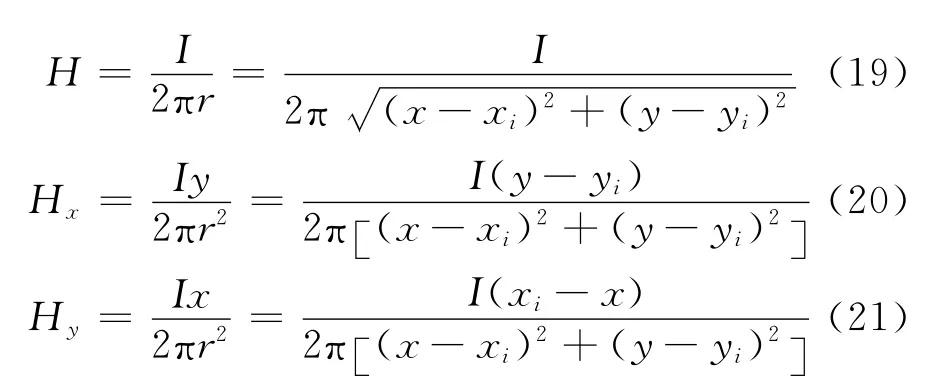
对于三相交流线路，三相对称电流IA、IB、IC的瞬时值为

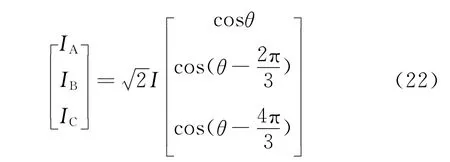
式中，I为电流的有效值，θ为A相电流的相位角.

三相对称电流IA、IB、IC在空间合成磁场分量：

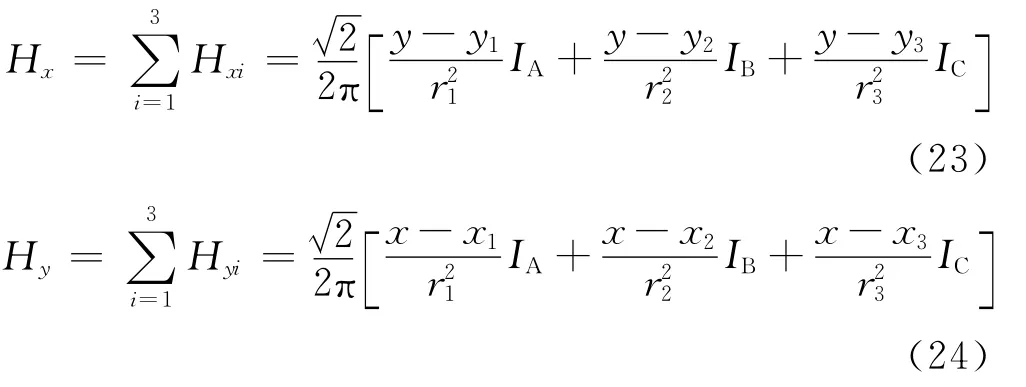
空间任一点的磁场强度：

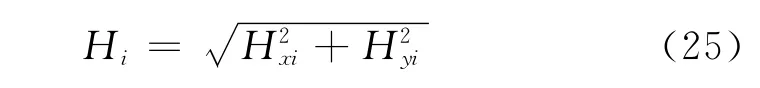
1.2.2 并行输电线路工频磁场的求解方法

由矢量叠加原理知多根导线在空间任一点产生的磁场强度等于每一根导线单独作用时在这一点产生磁场强度的叠加，即计算出线路各相导线所产生的空间磁场强度，并分别在平行于地面和垂直于地面进行投影，从而可采用矢量叠加进行并行线路的空间磁场的计算.

并行线路m根导线产生的磁场强度由叠加原理可得：

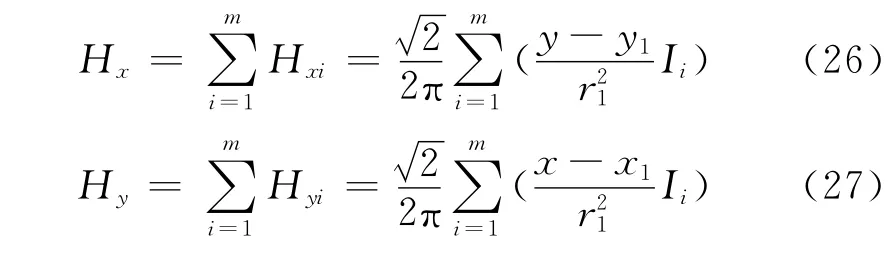
式中，Ii为第i根导线的电流瞬时值；ri为第i根导线到空间点的距离即

并行线路的磁场强度：

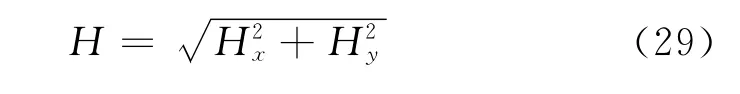
2 工频电磁场的结果分析

2.1 并行输电线路模型

三峡大学南苑并行输电线路包括2条电压等级均为110kV的同塔双回线路及1条电压等级为35 kV的单回输电线路，共3条线路并行，如图3所示.

图3 并行输电线路的塔型图片

三峡大学南苑并行输电线路参数的模型如图4所示，共计15条相导线.

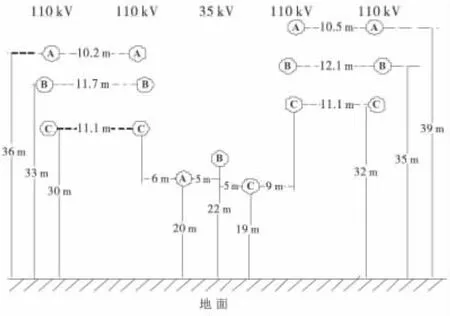
图4 三峡大学并行输电线路模型

2.2 工频电磁场测量试验

对工频电磁场进行的测量试验包括两部分：第一部分是对线路参数的测量，第二部分是对工频电磁场的测量.测量时间为2013年12月20日14：00，天气晴朗，风速1级.测量地点为三峡大学南苑，离公路较近.

2.2.1 线路参数的测量试验

试验测量各并行线路各相导线的对地距离，以及15条相导线之间各自的相对距离.为得到精确值，分别选择5个基准点进行5次重复测量，取平均值即可得到图4所示模型的距离参数值.测量仪器选用Bushnell 2－1000型号激光测距仪，该仪器误差为0.01m.

2.2.2 工频电磁场的测量试验

根据文献［9］对交流高压架空送电线路和变电站工频电场、磁场的测量仪器及测量方法的规定，以边相导线为基准，垂直于线路路径方向，测量工频电磁场的横向衰减特性.测量时，以5m为间隔，逐点测量距线路边导线50m内的工频电磁场强度.试验采用HI－3604型号工频电磁场强度测量仪，电场强度的测量精度为±0.05kV／m，磁场强度的测量精度为±0.01A／m.图5分别为型号 HI－3604的工频电磁场的测量仪图片及工频电磁场的现场实测图片.

图5 并行输电线路工频电磁场的测量图片

2.3 理论值与测量值的分析比较

2.3.1 工频电场理论值与测量值的分析比较

并行线路电场强度的测量结果与计算结果的对比如图6所示.由图6可知，电场强度横向分布的测量值与计算值变化趋势相同，但数据存在一定的误差.误差最大值为0.45kV／m，最小值为0.15kV／m.

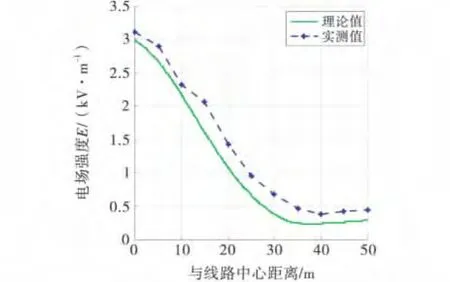
图6 电场强度的测量值与计算结果对比

误差产生的原因如下：1）线路模型的参数测量存在一定的误差，虽激光测距仪精度较高，但测量时由于导线在视距数十米外，激光测距时很难对准，因此存在人为操作误差；2）工频电场测量仪器存在一定的精度误差；3）由于电场是由电荷产生的，而电荷除了存在于导线中，还广泛存在于自然界中，空气、人体、动植物及邻近线路公路汽车通过都会引起测量点的电场变化，因此，电场测量受外界的影响较大，而这也是测量误差的主要来源.

2.3.2 工频磁场理论值与测量值的分析比较

图7为并行线路磁场强度的测量结果与计算结果的对比.由图7可知，磁场强度横向分布的测量值与计算值变化趋势相同，但数据存在一定的误差.磁场强度的误差最大值为0.25A／m，最小值为0.01A／m即磁感应强度误差的最大值为0.0003mT，最小值为0.00001mT.工频磁场的实测值比工频电场的精度要高.

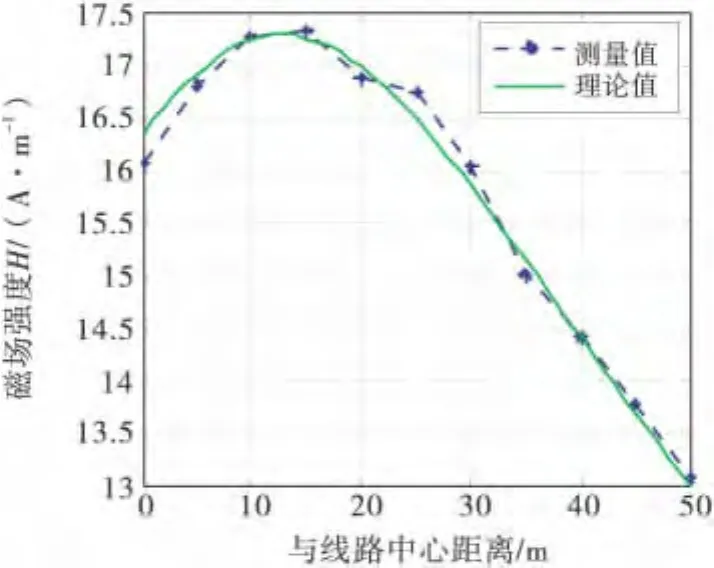
图7 磁场强度的测量值与计算结果对比

主要原因如下：1）工频磁场是由载流导体即电流产生，载流导体存在于导线中，受外界的干扰较小；2）工频磁场测量仪器的精度较高.因此，磁场测量较电场的测量更精确.

2.4 测量值与国际标准极限值的分析比较

1998年ICNIRP出版的《限制时变电场、磁场和电磁场暴露的导则》（300GHz以下的），对电磁辐射的暴露水平做了严格规定，根据ICNIRP的规定，一般民众的工频电场的极限值为5kV／m，工频磁场的极限值为100μT.由图6可知测量工频电场的极值为3kV／m，由图7可知工频磁场的极值为17.3A／m，由B＝μH可得工频磁场的测量极值为21.7μT，均在规定的范围之内.故三峡大学南苑的并行输电线路对人造成的危害可以忽略.

3 结 论

1）计算出线路各相导线所产生的空间电场、磁场强度，并分别在平行于地面和垂直于地面进行投影，从而可采用矢量叠加进行并行线路的空间电磁场计算.

2）以三峡大学南苑并行线路为例，采用叠加算法，工频电场最大误差值为0.45kV／m，工频磁场最大误差值为0.0003mT.

［1］赵建国，牛 林.日本特高压交流输电技术的研究与实践［J］.电力系统及其自动化学报，2007，19（1）：28－33.

［2］周 浩，余宇红.我国发展特高压输电中一些重要问题的讨论［J］.电网技术，2005，29（12）：1－9.

［3］中村秋夫，冈本浩，曹祥膦.东京电力公司的特高压输电技术应用现状［J］.电网技术，2005，29（6）：1－5.

［4］邬 雄，张文亮.电力系统电磁环境问题［J］.高电压技术，1997，23（4）：1－46.

［5］季道广.交直流并行输电线路电磁环境的研究［D］.济南：山东大学，2012.

［6］Sarma Maruvada P，Turgeon A，Goulet D L，et al.An Experimental Study of Residential Magnetic Fields in the Vicinity of Transmission Lines［J］.Power Delivery，IEEE Trans on，1998：1328－1334.

［7］倪光正.钱秀英.电磁场数值计算［M］.北京：北京高等教育出版社，1996.

［8］盛剑霓.工程电磁场数值分析［M］.西安：西安交通大学出版社，1991.

［9］刘华麟.高压输电线、变电站电磁场环境测量方法研究［D］.重庆：重庆大学，2005.