声波在室内的传播

赵其昌

（南京大学声学研究所，江苏 南京 210093）

声波在室内的传播

赵其昌

（南京大学声学研究所，江苏 南京 210093）

本文介绍了声源辐射的声波在室内传播时，因界面引起的简正振动模式，大房间的下限频率，室内声场的分布和混响、干涉对音质的影响。

简正振动模式；大房间下限频率；混响；干涉

剧院、音乐厅、会议厅和多功能厅等场所经常用到扩声系统。声波在室内的传播不同于室外，受到室内壁面的限制。声波传播到壁面上时，因为界面条件的不同会发生吸收、反射、扩散和透射等现象。那些返回的声波与入射的声波发生作用，于是出现了在室外传播中没有的现象，如驻波、声场的起伏和混响等。本文主要介绍声源辐射的声波在室内传播中出现的简正振动模式，声场的起伏，大房间的下限频率，室内声场的分布和稳态声压级，以及混响、干涉对音质的影响。

1 房间的简正频率

在室内传播的声音，我们只能听到，却看不见。图1是笔者在南京大学声学所审听室（改造前）测量的某扬声器的频率特性（扫频信号）。图2 是德累斯顿国家剧院用脉冲测试的结果。声音在室内传播出现很多紧挨的峰谷是怎么回事？而我们耳朵根本就没有感觉到这些“毛刺”的存在。这些峰谷是由于室内的简正振动模式引起的。声波在室内传播，可以用波在弦中的传播来类比。在一根绷直而两端固定的琴弦上拨一下，弦中出现各种频率的波，但是只有弦的两端为波节的波可以在弦中传播，否则很快就会衰减掉。这是因为弦的两端是固定的，不允许振动。假设弦的长度为l，弦中的张力为T，弦的线密度为，则在弦中允许传播的波的频率为：

其中，n为正整数，n=1,2,3……，fn称为弦的固有频率，如图3所示。

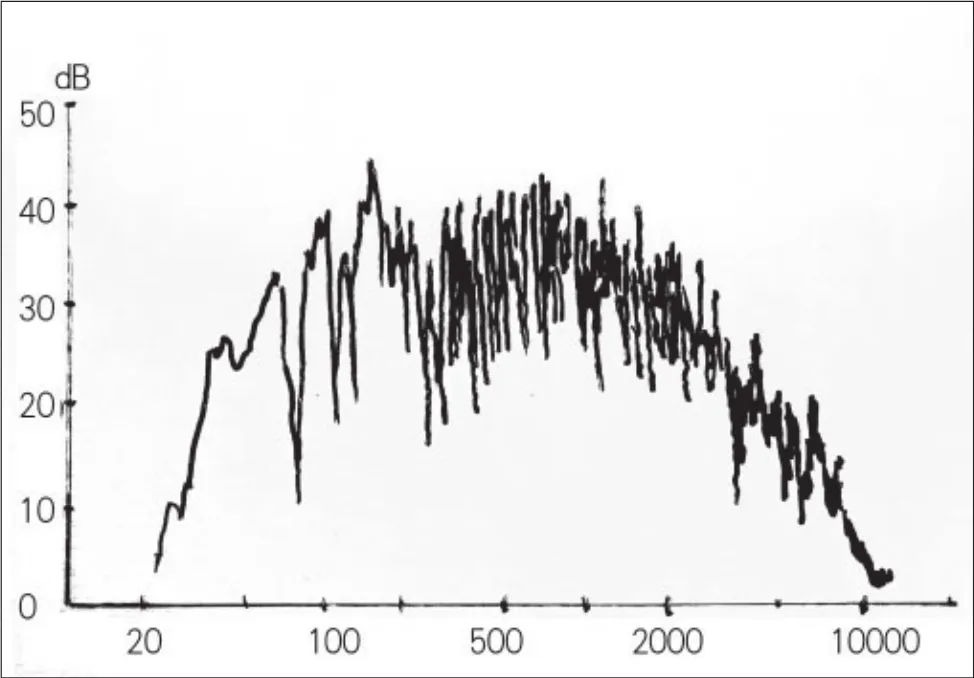
图1 扬声器的频率特性

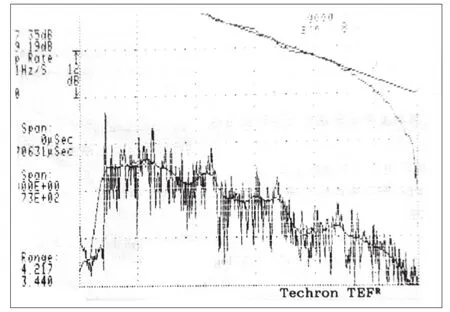
图2 德累斯顿国家大剧院的脉冲响应

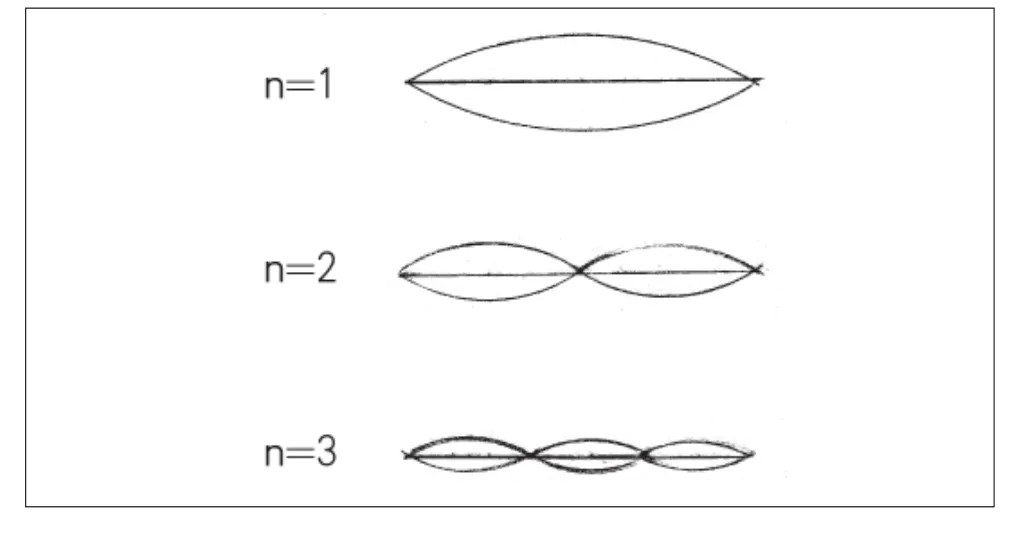
图3 弦的振动

在室内传播的波与弦中传播的波类似。在壁面坚硬的室内，只有在壁面处声压为极大的波才可以在两个平行且坚硬的壁面之间传播，否则就会很快衰减掉。图4为在一间尺寸为5 m×4 m×3 m的坚硬壁面的矩形房间内，在相对的两个顶角点上测得的传输响应和相应的计算结果。测量值与计算值非常接近。在房间内允许传播的波的频率，称为房间的简正振动频率，由式（2）决定：

式中：

室内的振动模式常以nx，ny，nz的取值来命名，

图4（1） 一间矩形房间的简正频率和传输特性

为什么人耳没有听出这些峰谷？这是因为人耳听觉的反应没有那么快。人耳的感觉是一个平均效果，平均时间大约为25 ms～30 ms。国家标准GB/T 12069.5-2011中规定，用纯音测量扬声器的频率响应时，小于1/9倍频程的峰谷不计，也正是这个原因，人耳听不出来。

如果希望知道在室内某一频率以下有多少个简正振动模式，可以用式（3）计算：

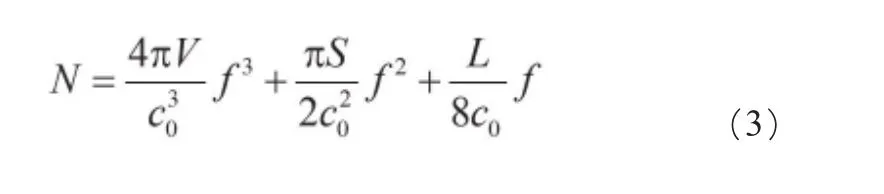
式中：

N——简正振动模式数；V——房间的体积；

式中第一项与频率的三次方成正比，所以总体上，某个频率的简正振动模式的个数与第一项的关系最大，即空间越大，简正振动模式越多；频率越高，简正振动模式也越多；空间小、频率低，则简正振动模式少，因此声场的起伏也大。如卡拉OK厅内声场一般起伏比较大，就是这个原因。

2 大房间的下限频率

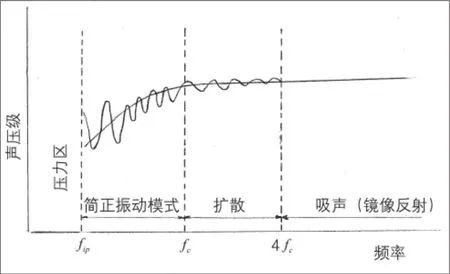
图5 室内声场随简正频率的变化

式中：

T60——混响时间；

V——房间体积。

这个公式可用于估算房间的大小。认为大于fc的那些频率将有大量的房间简正振动模式被声源的频率所激励振动。fc实际上是一个过渡区，并没有绝对意义上的频率分界线，但是可以估算出房间的基本要求。例如，设语言系统的下限频率为80 Hz，混响时间为1 s，则由式（4）计算可以得到房间的最小体积为625 m3。设音乐系统的下限频率为30 Hz，混响时间为1.8 s，用式（4）计算得到房间的最小体积为8 000 m3。当频率大于fc时，室内的简正振动模式数较多，到达空间某一点的声波的叠加使声场的起伏变小，这时可以用统计声学或几何声学来处理室内的声学问题。

对于小于fc的房间，一般声场的起伏比较大。这时可以改变房间的形状，增加室内声波的散射和加大壁面的阻尼来减小声场的起伏。最新的技术是通过数字声系统处理技术，对声场中的某些点采用合适的算法。如粒子群优化算法，提高小型房间内低频重放优化的计算效率，通过算法得出系统优化系数、增益、滤波中心频率、Q值、均衡量和延时等，可以切实有效地改善小型房间内的声场特性。

3 室内声场分布

假设将扬声器置于室内的一个墙角处，则室内某一点的声压来自于扬声器的直接辐射和壁面的反射两部分。在扬声器的远场区域，直接辐射部分的声波以离开声源的距离每增加一倍即衰减6 dB的规律传播。离声源的距离越近，声压级越高，这时壁面的反射波与直达声波相比较小，该区域以直达声波为主。当离开声源的距离较远时，直达声波衰减较快，小于壁面反射声波，该区域以反射声波为主。声压随距离的变化见图6。直达声能与反射声能之比，随离开声源的距离的增加是逐步变化的，当直达声能等于反射声能时，离开声源的距离称为混响半径（有的书上对于点声源称为混响半径，对于有指向性的声源称为临界距离）。混响半径的表达式为：

图6 室内声压随距离的变化

式中：

Q——声源的指向性因数；

V——室内体积，单位为m3；

T60——混响时间，单位为s。

混响半径与声源的指向性因数有关。对于点声源，Q=1，指向性因数越大，则混响半径越大，直达声的区域也越大。直达声区域还与室内体积有关，空间越大，直达声区域也越大。此外，混响半径还与混响时间有关，混响时间越长，则混响半径越小，直达声区域也越小。在扩声工程中，直达声区域大一些的听音效果较好。在直达声为主的区域听音，声音清晰、层次分明、声像感好。当然，如果调试不好，声干涉也越大。对于一个建好的厅堂（体积确定，混响时间一定），直达声区域取决于声源的指向特性。例如，某厅堂V=10 000 m3， T60=1 s，如选用Q=5的扬声器，则混响半径rc=13.4 m；如选用Q=20的扬声器，则rc=26.8 m。所以，在厅堂内扩声常选用指向性较好的扩声系统。另外，声源的指向特性还与室内语言清晰度的重要指标——辅音损失有关。

在大于混响半径的区域，因为直达声随距离的增加衰减很快，而反射声比较强，该区域以混响声为主。混响声的主要特点是，到达观众位置的声音来自各个方向，相位无规，因此，声波之间不会发生干涉，声场也比较均匀，但是声音的清晰度和层次感会受到影响。

在室内的壁面附近，对声波而言是界面的干涉区，有入射声波和反射声波。在一般没有经过声处理的墙面上，反射波声压与入射波声压是同相的，叠加相干，故在离界面1/4波长的范围内是声压级比中间平均值要高的界面干涉区，壁面处声压级比中间平均值高3 dB，棱线比中间高6 dB，顶角比中间高9 dB。因此，在测量声场不均匀度时，要求测点必须离开壁面1/2波长，避开壁面干涉区。

4 稳态声压级

声源在室内发声达到稳定以后，室内的声能量由两部分组成：直达声能与混响声能。直达声的强度与传播距离r的平方成反比，混响声能在每一处都是多次反射的叠加。按统计声学，可认为各处都是相等的，由此可以计算得到在距离声源r处的声压级Lp。当然，室内的声能量与声源的辐射声功率密切相关。因此，室内的稳态声压级为：

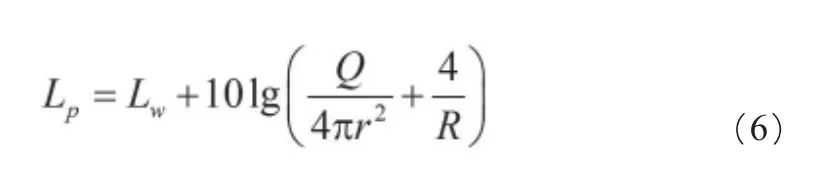
式中：

LW——声源的声功率级；

Q——声源的指向性因数，是方向的函数；

r——离开声源的距离；

R——房间常数，它与房间界面的内表面积S和界面的平均吸声系数有关，。

式（6）括号中的第一项是直达声的贡献，随着离开声源的距离r的增加，直达声能以r2的速度下降，同时随声源的指向性因数的增加而增加。Q是频率的函数，一般声源在低频时无指向Q ≈1，随着频率的增加Q会增加，不同的声源变化不一样。Q同样是方向的函数，常用声源主轴方向的指向性因数来估算。第二项是混响声能的贡献，它与房间的内表面积和平均吸声系数有关。空间越大，内表面积的平均吸声系数越大，则房间常数越大，混响声能对总声压级的贡献就越小。

例如，已知某厅堂V=10 000 m3，T60=1 s，扬声器系统的Q=10，特性灵敏度L1m,1w=103 dB，额定功率为300 W，要求估算厅堂内的稳态声压级 。

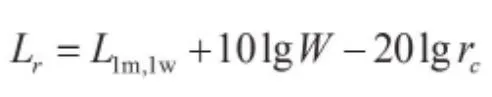
5 混响

至今判断室内声场音质的主要参数仍然是混响时间。混响时间的概念是1900年W.C.Sabine（赛宾）在美国《建筑》杂志上发表的《混响》一文中首先提出的，开创了建筑声学的研究。经过4年的研究，赛宾给出了厅堂混响时间的经验公式：

式中：

V——室内的体积；

A——该空间的声吸收总量；，

S——内总表面积；

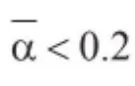
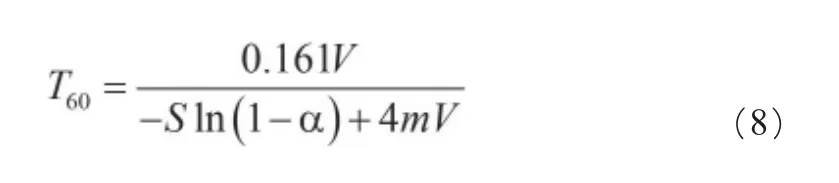
式中：

m——声波在空气中传播的衰减系数，它是温度、湿度和频率的函数。

从赛宾开始经历了一百多年，建筑声学有了很大发展。但是混响时间仍然是室内音质设计的最基本量。对于一定容积的厅堂，混响时间决定于室内所用的材料的吸声性能和总的吸声量。经进一步的研究，E.N.Gilbert在原理上说明混响时间与房间形状、材料分布和不同接收点位置都有关系。同样吸声性能和面积的吸声材料放在房间的一面墙上和放在墙角上，它的吸声效果是不同的，因此，混响时间也不一样。这是在混响理论上的重大进展。所以，在室内声学设计时，除了要考虑材料的吸声系数本身有一定误差外，还要考虑材料铺设在不同位置时其吸声效果也会有所不同。

在建筑设计上，对音质不利的声音，如多次反射形成过长的混响声，原先的方法是将其吸收掉，而最新的观点是通过结构的设计将其反射掉，从而避免对听众区起作用，可以大大地节省吸声处理的费用。如，在机场的候机大厅或火车站的候车室，一般空间都比较大，壁面又多采用玻璃结构，吸声性能很差。传统的做法是在玻璃表面铺设微穿孔的透明薄膜吸声，造价很高。新的做法是将玻璃墙面做成斜面，让不需要的反射声经过壁面而不会反射到乘客区，避免多次反射形成混响，影响声音的清晰度。

6 声波的干涉

在自由空间传播的声波，其相干的条件是两列波的频率要相同、相位差要固定。满足该条件的两列波在空间相遇，其叠加的结果是可能相消为零，也可能相加，增加6 dB。相消还是相加取决于相位，相位相反则相消或减弱，相位相同则相加或增强。其减弱或增强的程度取决于声的振幅。图7是两列强度不同的波的干涉图形。一条是声压、时间差为0.1 ms时的曲线，幅度变化比较大，即声场干涉比较厉害。一条是声压、时间差为0.2 ms时的曲线，幅度变化比较小。很显然，两列波的声压级差不多时的干涉最大，对声场的影响也大。所以声场调试时，要求寻找两扬声器声压级相等的辐射区，在该区域进行补偿，取得的效果最好。

（4）声音大多是复合音，对于空间某一点到达的两列波的相位差为180 °时两列波相消，干涉结果为一谷点，满足该条件的不同频率都会形成谷点，将代入式（11），则：

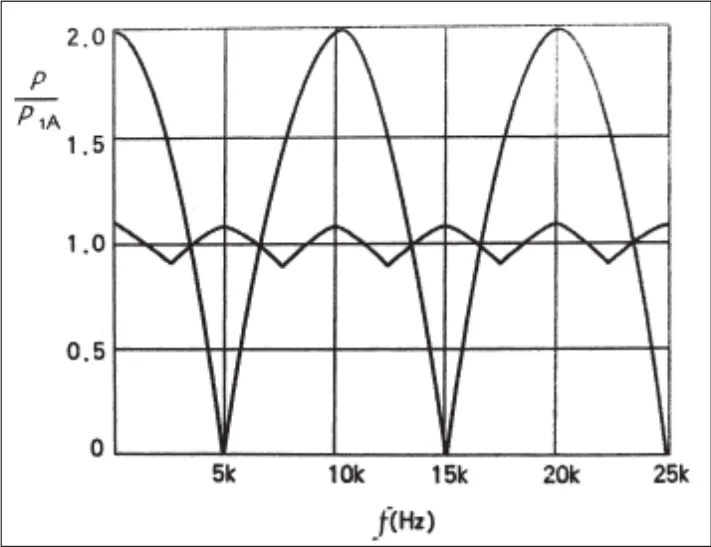
图7 梳状滤波效应

表1 第一个零点出现的频率与时间差的关系以及两零点的频率间隔与的关系

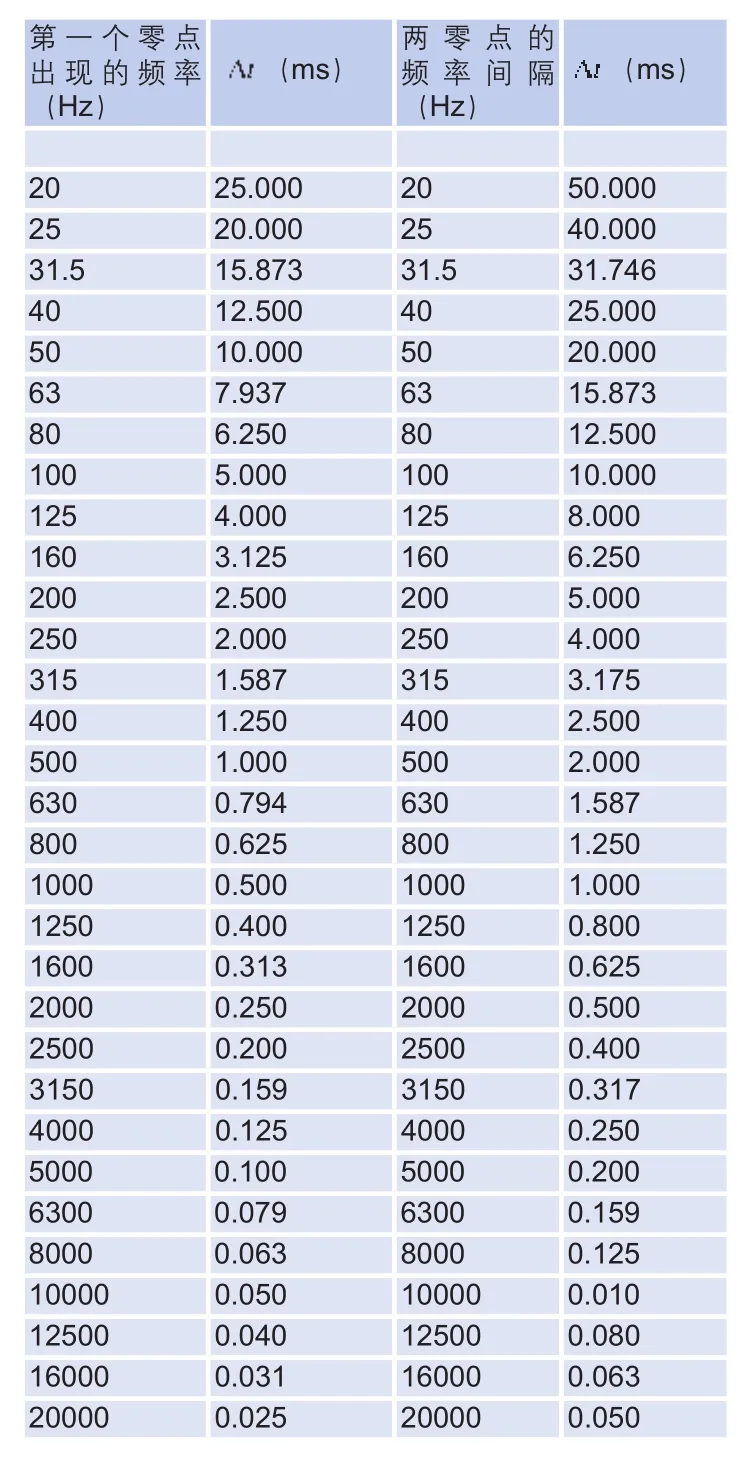
表1 第一个零点出现的频率与时间差的关系以及两零点的频率间隔与的关系

第一个零点出现的频率（H z）（m s）两零点的频率间隔（H z）（m s ）2 0 2 5 . 0 0 0 2 0 5 0 . 0 0 0 2 5 2 0 . 0 0 0 2 5 4 0 . 0 0 0 3 1 . 5 1 5 . 8 7 3 3 1 . 5 3 1 . 7 4 6 4 0 1 2 . 5 0 0 4 0 2 5 . 0 0 0 5 0 1 0 . 0 0 0 5 0 2 0 . 0 0 0 6 3 7 . 9 3 7 6 3 1 5 . 8 7 3 8 0 6 . 2 5 0 8 0 1 2 . 5 0 0 1 0 0 5 . 0 0 0 1 0 0 1 0 . 0 0 0 1 2 5 4 . 0 0 0 1 2 5 8 . 0 0 0 1 6 0 3 . 1 2 5 1 6 0 6 . 2 5 0 2 0 0 2 . 5 0 0 2 0 0 5 . 0 0 0 2 5 0 2 . 0 0 0 2 5 0 4 . 0 0 0 3 1 5 1 . 5 8 7 3 1 5 3 . 1 7 5 4 0 0 1 . 2 5 0 4 0 0 2 . 5 0 0 5 0 0 1 . 0 0 0 5 0 0 2 . 0 0 0 6 3 0 0 . 7 9 4 6 3 0 1 . 5 8 7 8 0 0 0 . 6 2 5 8 0 0 1 . 2 5 0 1 0 0 0 0 . 5 0 0 1 0 0 0 1 . 0 0 0 1 2 5 0 0 . 4 0 0 1 2 5 0 0 . 8 0 0 1 6 0 0 0 . 3 1 3 1 6 0 0 0 . 6 2 5 2 0 0 0 0 . 2 5 0 2 0 0 0 0 . 5 0 0 2 5 0 0 0 . 2 0 0 2 5 0 0 0 . 4 0 0 3 1 5 0 0 . 1 5 9 3 1 5 0 0 . 3 1 7 4 0 0 0 0 . 1 2 5 4 0 0 0 0 . 2 5 0 5 0 0 0 0 . 1 0 0 5 0 0 0 0 . 2 0 0 6 3 0 0 0 . 0 7 9 6 3 0 0 0 . 1 5 9 8 0 0 0 0 . 0 6 3 8 0 0 0 0 . 1 2 5 1 0 0 0 0 0 . 0 5 0 1 0 0 0 0 0 . 0 1 0 1 2 5 0 0 0 . 0 4 0 1 2 5 0 0 0 . 0 8 0 1 6 0 0 0 0 . 0 3 1 1 6 0 0 0 0 . 0 6 3 2 0 0 0 0 0 . 0 2 5 2 0 0 0 0 0 . 0 5 0

图8 典型的梳状滤波曲线

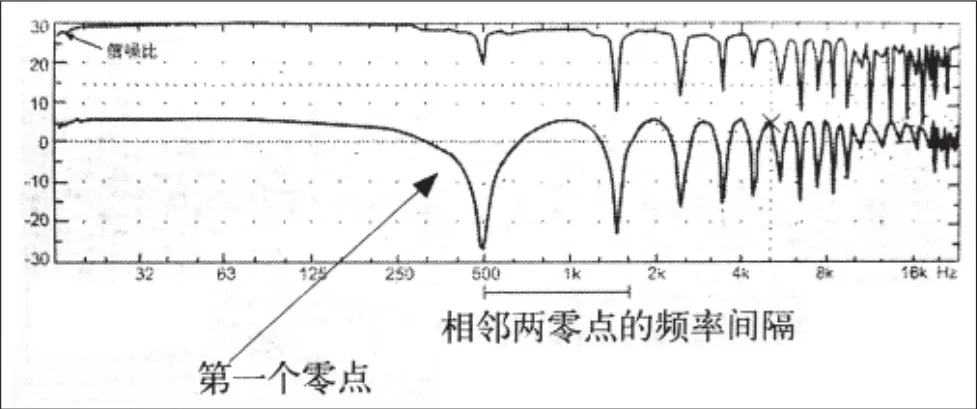
图9 直达声与反射声干涉的图形

两列相干波在空间某一位置发生干涉，在频率域上随频率的变化，声压变化出现一系列的峰谷，这一现象称为梳状滤波效应。图8给出了典型的梳状滤波曲线。图9是用SIM测试仪实测的直达声与反射声干涉的图形。反射声与直达声时间上滞后1 ms，强度上中频、高频有吸收。SIM测试仪可以现场直接观察干涉的幅频响应和相频响应，为现场调试提供指导。

笔者在广州励丰声光科技有限公司（简称“励丰”）的实验室看到的消声室，可以模拟剧场安装的扬声器系统的声干涉。在剧场中扬声器系统安装好后，需要调试。工程效果的好坏很大程度上取决于调试，这是我国扩声工程的一个薄弱环节。往往会出现这边调好、那边变坏的情况，单凭主观经验，缺少客观手段。声波的干涉主要在直达声区域，这是听音最好的区域，也是干涉最厉害的区域。“励丰”在实验室内做模拟试验，为现场调试提供依据，不失为一个好方法。

[1]赵其昌等. 现代音响技术和工程基础[M]. 南京：南京大学出版社，1999.

[2]杜功焕等. 声学基础[M]. 南京：南京大学出版社，2001.

[3]W·阿诺德，F·斯蒂芬. 扩声技术原理及其应用[M]. 王季卿，赵其昌，译. 北京：北京电子工业出版社，2003.

[4][德]赫尔姆特·富克斯. 噪声控制与声舒适[M]. 汪涛，查雪琴，译.北京：中国科学技术出版社，2012.

[5]赵其昌. 声场的干涉与时间延迟[J]. 演艺设备与科技，2004（5）.

[6]孙广荣. 室内声学解析[J]. 电声技术，2012（8）.

[7]刘紫赟. 小型房间内的低频声重放优化研究[D]. 南京：南京大学声学所，2012.

[8]D·戴维斯等. 声系统工程（内部资料）. 丁永生，翁泰来，崔广中，译.

（编辑 薛云霞）

The Transmission of Sound Wave in the Indoors

ZHAO Qi-chang
(Institute of Acoustics of Nanjing University, Nanjing Jiangsu 210093, China)

The normal mode of vibration，the low limited freguency of a room and the distribution of sound field were introduced in the paper. In addition, the influence on the tone quality by the reverberation and the inter-ference were expounded.

normal mode of vibration; low limited frequency of a room; reverberation; interference

10.3969/j.issn.1674-8239.2014.02.004