城市商业中心区机械式立体车库规划模型与算法

陈 莉，王同洲，宋结焱，王 娜，段 刚

（1.兰州城市学院，数学学院，兰州 730070；2.中铁集装箱运输有限责任公司，兰州分公司，兰州 730070；3.兰州交通大学，交通运输学院，兰州 730070）

1 引言

国家统计局的统计公报显示[1]，2012年末全国民用汽车保有量达到12089万辆，比上一年末增长14.3%，其中私人车9309万辆，增长率为18.3%.汽车保有量的快速增长产生了巨大的停车需求.一般情况下，机动车（出租车除外）只有10%-20%的时间是在路上行驶，80%-90%的时间需要停泊，而现有停车场车位远远满足不了需求.《中国城市发展报告2011》指出[2]，若按照“一车一基本车位，15辆车一公共停车场”的国际惯例，我国城市停车位缺口将高达50%以上.因此，加快我国城市公共停车场的建设步伐刻不容缓.

传统停车场占地面积大，平均需10平方米停一辆车，这对城市商业中心区等车辆集中且寸土寸金的区域来说，难以提供足够的车位.而机械式立体车库停一辆车平均只需1-2平方米，占地少，容量大，泊车与取车全自动化，节能环保，减少了车辆在车库内的尾气排放和噪声污染.所以建立机械式立体停车库是未来城市停车场发展的必然趋势.

停车场规划以城市规划和城市道路交通规划为依据，主要考虑停车场的选址、规模和收费标准等因素.众多学者对此进行了研究，文献[3,4]建立了城市公共停车场选址优化模型.目前，对立体车库选址问题的研究尚不多见，文献[5]和[6]分别利用粗糙集和GIS空间分析的方法对其进行了探索.文献[7]考虑了停车场规模问题，文献[8]对路内停车定价问题进行了优化，文献[9]同时对停车场选址和收费问题进行了优化，文献[10]则研究了停车场停车费和规模问题.但同时考虑这三种影响因素的文献还不多见.本文针对商业中心区用地紧张，传统停车场车位不足的情况，计划建立机械式立体车库，并同时考虑车库的选址、车位数量及收费这三个因素，建立综合优化模型，为市政部门提供决策依据.

2 模 型

2.1 问题描述

在一个商业中心区中包含一些商业点，由于大量驾车出行者到达这些商业点导致停车需求过大，需要在给定的候选地点中新建若干立体车库，且每个候选地点最多只能建一个.由于受到资金、土地及运营等方面的限制，还需要确定立体车库的规模（停车车位数量）及收费标准.将商业中心区产生的停车需求按出行者出行目的不同分为两种：一种是由于雇员上班引起的长时间停车需求，另一种是由于购物、娱乐等商业活动引起的短时间停车需求.出行目的不同的出行者会根据立体车库距离其目的地（商业点）的远近、收费和停车时间选择不同的立体车库存取车.目标是在投资回报期限内，使得立体车库运营总收入与投资成本之差（即利润）最大化.

2.2 参数与变量设置

（1）参数设置.

K——商业点集合；

L——出行目的集合；

I——立体车库候选地址集合；

J——立体车库规模集合；

T——投资回报期（年）；

Nkl——到商业点k出行目的为l的出行者数，即停车需求，k∈K,l∈L；

tkl——商业点k出行目的l的出行者的平均停车时间，k∈K,l∈L；

dik——候选地点i到商业点k的距离，i∈I,l∈L；

aj——立体车库规模为j时的投资（可变）成本，j∈J；

bj——规模为j的车库的可用车位数，j∈J；

cj——规模为j的立体车库层数，j∈J；

sj——规模为j的车库每层每个车位的平均面积，j∈J；

Ri——候选地址i的可利用土地面积，i∈I；

f——资金预算；

Ci——在候选地点i修建一个车库的固定成本；

eu,ed——分别为最高和最低收费标准；

αu,αd——立体车库的利用率上下限；

v——平均步行速度；

θl——出行目的l的出行者的时间价值转换参数，l∈L；

β1,β2——效用调节参数.

（2）变量设置.

yi=新建立体车库i的收费，i∈I，元/小时辆；

qikl=到达商业点k且出行目的为l的驾车出行者选择立体车库i的数量，i∈I,k∈K,l∈L

2.3 目标函数

停车费为立体车库的唯一收入来源，收费标准以小时为单位，通常有两种计费方法：一是与停车时间成正比；二是分段计费，且停车时间越长费用增加越多，比如停车1小时内费用为10元，2小时内第2小时为15元，3小时内第3小时为20元，以此类推.分段计费的目的是为了减少停车时间，高效的利用停车设施，主要是限制到商业中心区购物休闲的这部分出行者的停车时间.但对商业中心区内的工作人员来说，其停车时间往往是一天（按8小时计算），所以分段计费的方式对他们很不公平，而且难以根据停车时间的长短来区分出行目的，因此我们采用第一种计费方式.

以一年365天计算，在投资回报期T内，新建车库的总收费为 365T，而总成本为固定成本与可变成本之和，所以，目标为利润F最大：

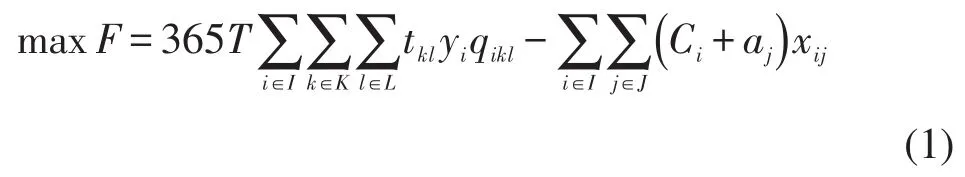
2.4 约束条件

(1)每个候选地点最多只能建立一种规模的立体车库.

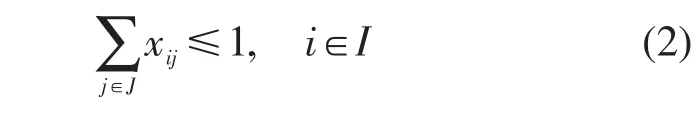
(2)收费限制.

式中 M为非常大的正数，式(3)表示只有在候选地点新建立体车库才能收费.

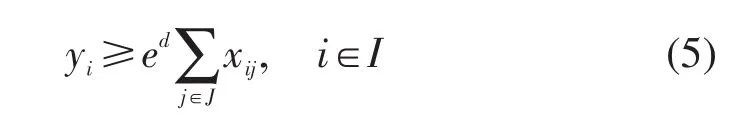
式(6)和式(7)表示分别表示收费上下限.

(3)资金预算限制.

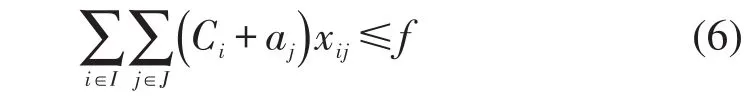
(4)可利用土地面积限制.

(5)所有新建立体车库提供的车位数应满足总停车需求.

(6)新建立体车库利用率要求.

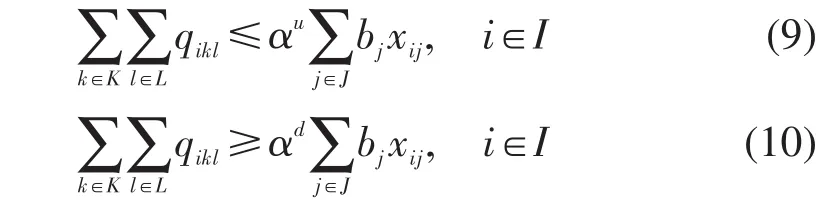
(7)出行者对立体车库的选择.

出行者通过步行到达立体车库的时间和停车费（停车时间乘以单位费用）来选择立体车库，并通过时间价值转化参数θl将步行时间转化为费用，将两者单位统一，应用Logit分担率计算每个立体车库吸引出行者停车的数量.

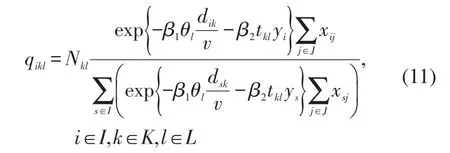
(8)变量声明.

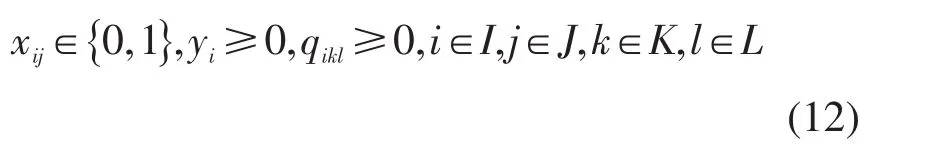
3 求解算法

我们采用遗传算法进行求解.虽然遗传算法具有简单、鲁棒性好和并行计算等优点，但其最大的不足之处在于早熟，即搜索过程过早地陷入局部最优解.克服该缺点的方法有很多，比如在搜索过程中嵌入禁忌搜索、模拟退火[11]等算法.遗传算法是建立在种群多样性基础上的启发式方法，在计算过程中，一旦种群多样性遭到破坏，便会陷入早熟，因此本文设计了基于种群多样性控制策略的遗传算法.

3.1 种群多样性

本文采用的遗传算法将解分为可行解与不可行解两种，并分别放入两个子种群中，在运算过程中始终保持一定数量的不可行解，这样无疑可以扩大种群多样性.通过对可行解与不可行解的交叉、变异等运算，能够得到更接近搜索空间边界的解，这也是高质量解经常出现的地方.

当迭代一定代数后，当前最优个体仍没有改变，说明有可能陷入局部最优，此时通过引入一定数量的新个体以代替部分当前个体，从而扩大种群多样性.为提高计算效率，我们将当前种群中评价值最好的那部分个体保留，替代的都是那些评价值差的个体.其中，新个体的产生与后面介绍的初始化种群的方法相同.

3.2 染色体编码与解码

采用整数编码，由数量不同的基因组构成，每个基因组包含新建立体车库地址、规模及收费三个信息.由于每个染色体的长度不同，为便于后续操作，我们将新建立体车库的总数统计后放在每个染色体的最前方.在图1的染色体P中，第一组基因(3,2,15)表示在候选地3建立规模为2的立体车库，收费为15元，后两组基因含义与此相同.由于一共建立了3个立体车库，所以我们将3放在染色体中0的位置.因此该染色体的长度为4.

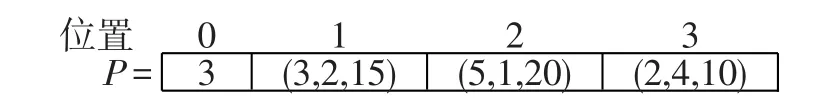
图1 染色体的表示方法Fig.1 The representation scheme of chromosome

显然，该染色体对应的解为：x32=1,x51=1,x24=1,y3=15,y5=20,y2=10 ，而 qikl则由式(11)计算得到.

3.3 个体评价值

为使种群多样化，我们扩大搜索空间，通过放松约束条件将不可行解包含进来.令γh(h=1,2)和(h=1,2,3,i∈I)为惩罚因子，并定义函数

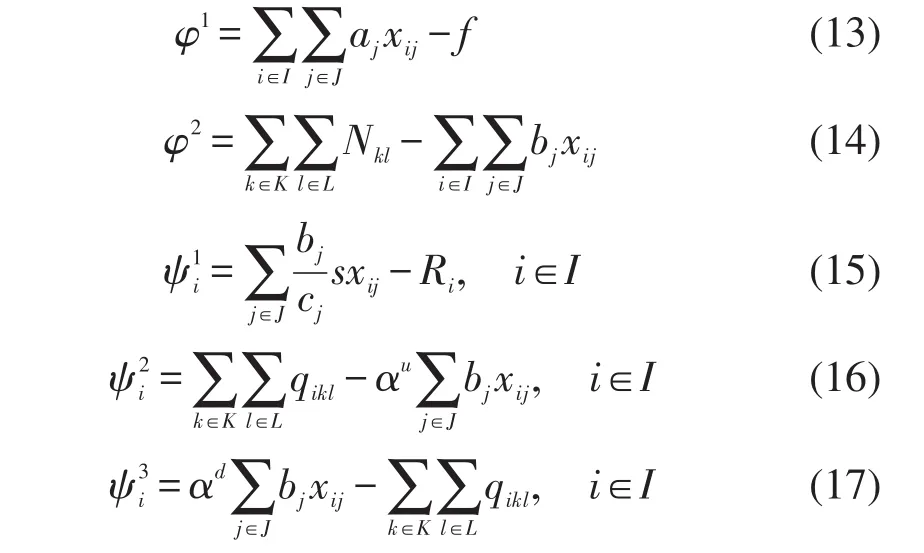
于是，我们将惩罚因子和上述定义的函数进行加权，并同模型中的目标函数求代数和，得到个体P的评价函数为

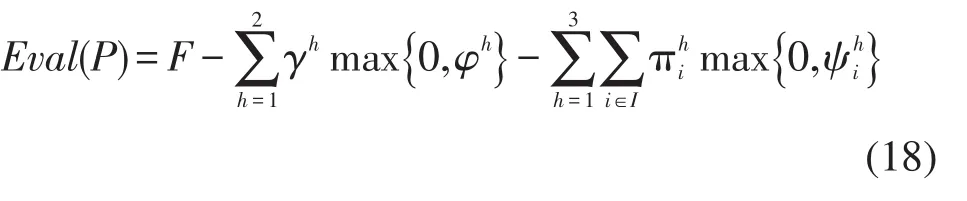
3.4 交叉与变异

交叉操作采用下面的方法.分别令n1和n2为父染色体P1和P2的新建车库数，即两个染色体第0个位置的值.随机产生两个整数n3∈[1 ,n1]和n4∈[1 ,n2]，然后将染色体P1的n3到n1位基因组和染色体P2的n4到n2位基因组进行交换，得到两个子染色体C1和C2，它们的新建车库数分别为n3+n2-n4和n4+n1-n3.为使交叉操作有效进行，n3和n4不同时为1.例如当n1=3,n2=5,n3=1,n4=4时，两个染色体的交叉操作如图2所示.

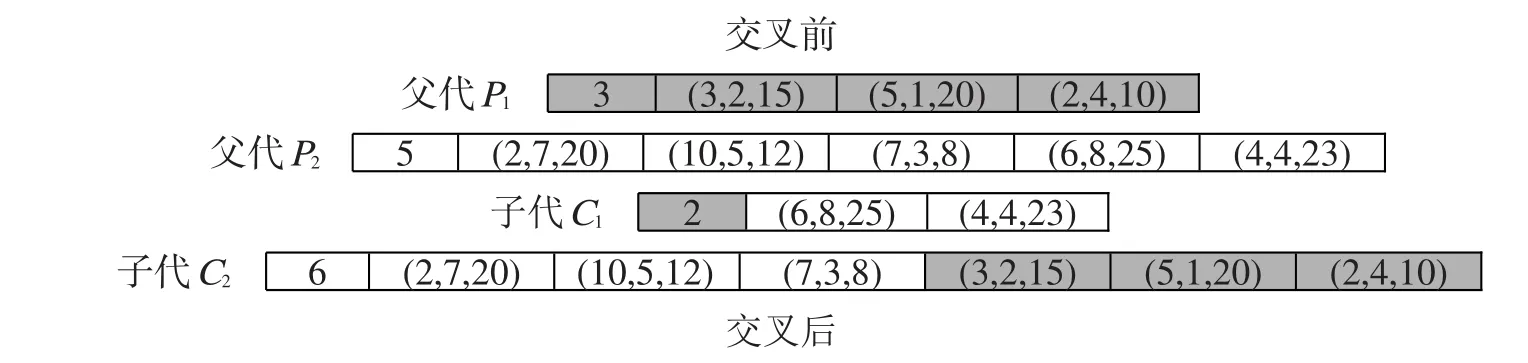
图2 染色体交叉操作Fig.2 Crossover of two chromosomes

由于子代染色体C2包含相同的候选地点，所以需要调整，只需删去任意一个候选地点相同的基因组即可，并同时对新建车库数量进行调整.调整后的染色体C3如图3所示.

图3 染色体的调整Fig.3 Repair of the chromosome

采用三种方式进行变异操作，分别为：

(1)对候选地址进行调整，随机选择一个在染色体中没有出现的候选地点，替换该地点；

(2)对车库规模进行调整，随机产生一个不同的车库规模替换该规模；

(3)对收费进行调整，随机产生一个收费替换该费用.

在染色体的所有基因组中（不包括第0位）随机产生一个位置，在三种变异方式中随机选择一个，对相应基因进行调整.

3.5 种群初始化及管理

采用下面的方法产生染色体：随机生成一个整数n，1≤n≤ ||I，其中 ||I为候选地点个数，染色体的长度为n+1.然后随机产生n个不同的整数（范围在1到 ||I之间），作为建立车库的地点依次放入染色体的每个基因组中；再从车库规模集合中随机选择n个整数，依次放入染色体的每个基因组中；最后为每个基因组随机产生一个费用.共产生PS个染色体作为初始种群.

得到的解根据其可行性分别归入可行解子种群和不可行解子种群，并记录可行解种群中评价值最好的个体.在交叉和变异后可能导致解的不可行性，这样会减少可行解的数量，为保持两个子种群的合理比例，我们通过变化罚因子的大小来调节种群的数量.令Nf表示当前迭代可行解子种群中染色体数量，Ninf表示当前迭代不可行解子种群中染色体数量，则二者的比例σ为

定义一个目标比例σ0，当迭代若干代后，比较二者的大小，若相差过大，则对3.3节中的罚因子γh进行如下调整：罚因子πhi的调整与之相同.

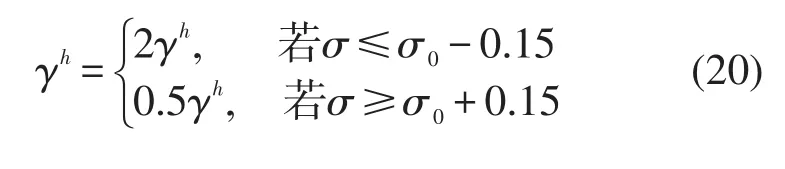
4 算例分析

我们以一个商业中心区为例，对本文建立的模型和设计的算法进行验证.根据该中心商业布局特点，我们将其划分为6个商业点，将出行目的分为上班和购物两种，计划在10个候选地点进行选址，共有12种规模的立体车库可供选择.商业点及候选地点位置如图4所示.修建一个立体车库的投资回报期限为20年，收费最低和最高标准分别为5元/小时和30元/小时，资金预算为4千万元.假定每个立体车库的利用率上限为95%，下限为70%.上班出行者的平均停车时间为8小时，购物休闲出行者的平均停车时间为3小时，平均步行速度为5 km/h.上班出行者的时间价值转换参数为2，购物休闲出行者的时间价值转换参数为1，效用调节参数 β1=1,β2=0.005.其余信息如表1—表4所示.

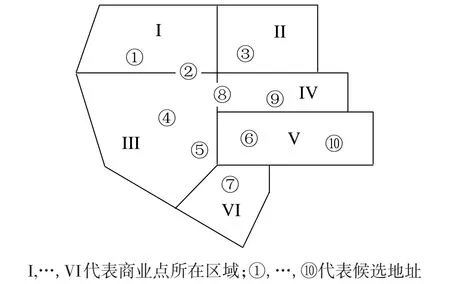
图4 商业中心区示意图Fig.4 The central business district diagram

表1 停车需求（辆）Table 1 Parking demand（vehicle）

表2 候选地点与商业点距离（公里）Table 2 The distance between candidate location and business site（kilometer）

表3 车位信息Table 3 Berth information

由于遗传算法对交叉概率和变异概率的选取较为敏感，因此为了寻求二者的最佳取值，我们采用VC++6.0编程，在配置为AMD速龙™II×4645(3.1GHz)、2G DDR3 SDRM台式机上，对两种概率组合分别做20次测试.首先取变异概率为0.1，交叉概率每次变化0.05，评价值的平均值如图5所示，得到交叉概率的最优值为0.9.在此概率下，变异概率每次变化0.1，得到评价值的平均值如图6所示，变异概率的最优值为0.6.其余参数分别为遗传代数1000，种群规模PS=40，目标比例σ0=60%，初始罚因子γh=10=1.每经过50代对罚因子进行一次调整，每运算100代调整一次种群多样性，每次调整替换种群中70%的个体.

表4 候选地点信息Table 4 Candidate location information

为说明上述提高种群多样性所采取的多种方法的有效性，我们将一般的遗传算法（没有区分可行解与不可行解并调整二者比例，也没有对种群的部分个体进行替换）与本文提出的基于种群多样性控制的遗传算法进行对比，结果如图7所示.前者在450代就已经收敛，充分说明了其早熟性，而本文提出的方法在迭代的最后阶段（870代）评价值仍有改善.

在得到的方案中，一共新建8个立体车库，分别在候选地点4，5和7建立一个25层150个车位的车库，在地点3和9分别建立一个20层160个车位的车库，在地点2，6和8分别建立一个25层200个车位的车库，总共提供1370个车位（总需求为1228个）.

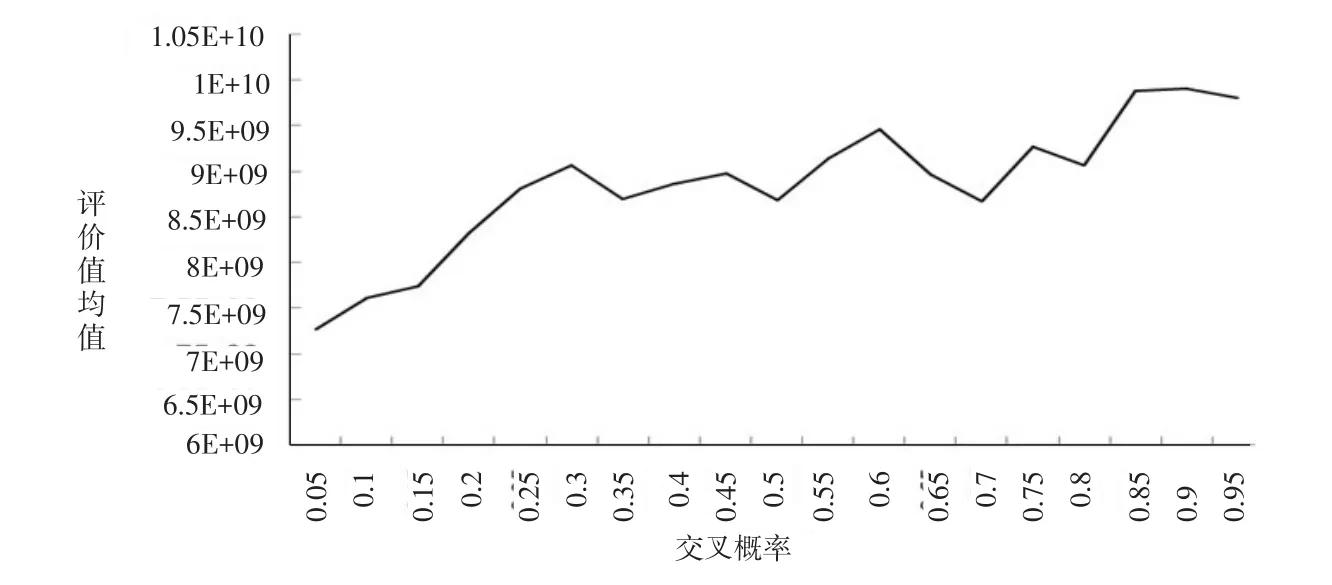
图5 交叉概率测试Fig.5 The test of crossover probability

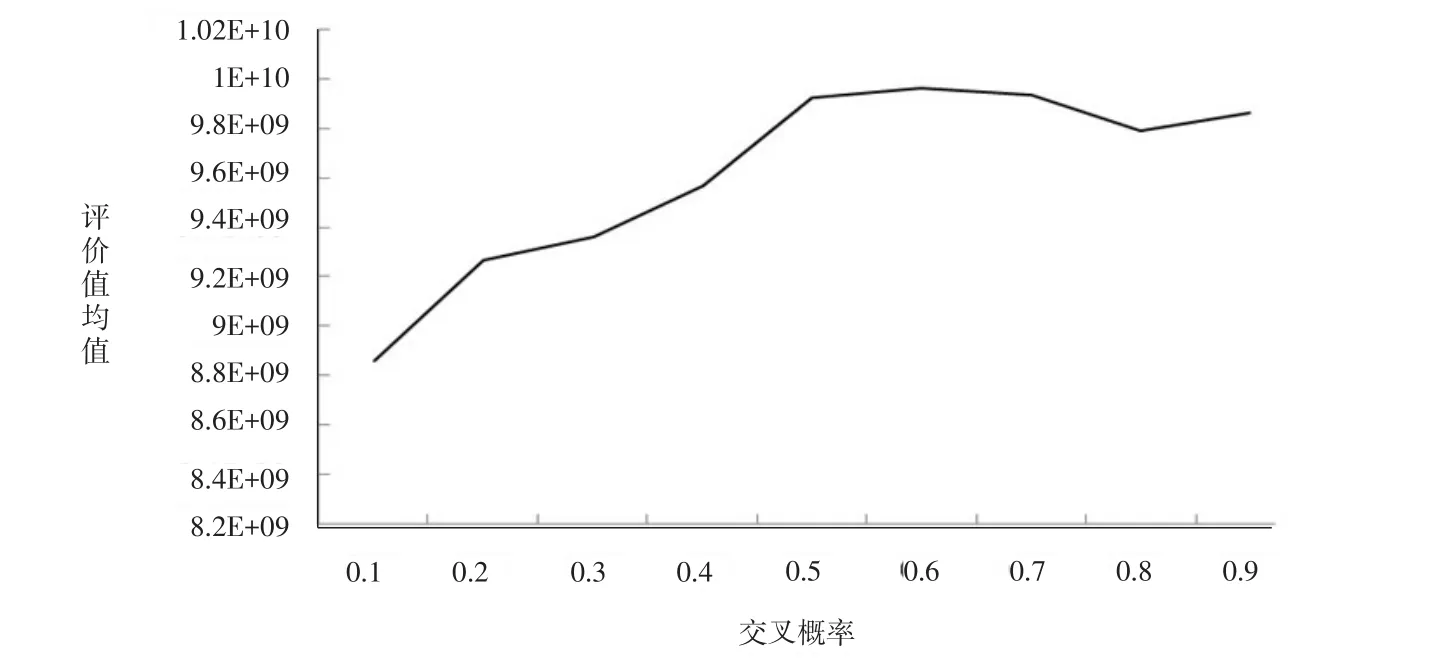
图6 变异概率测试Fig.6 The test of mutation probability

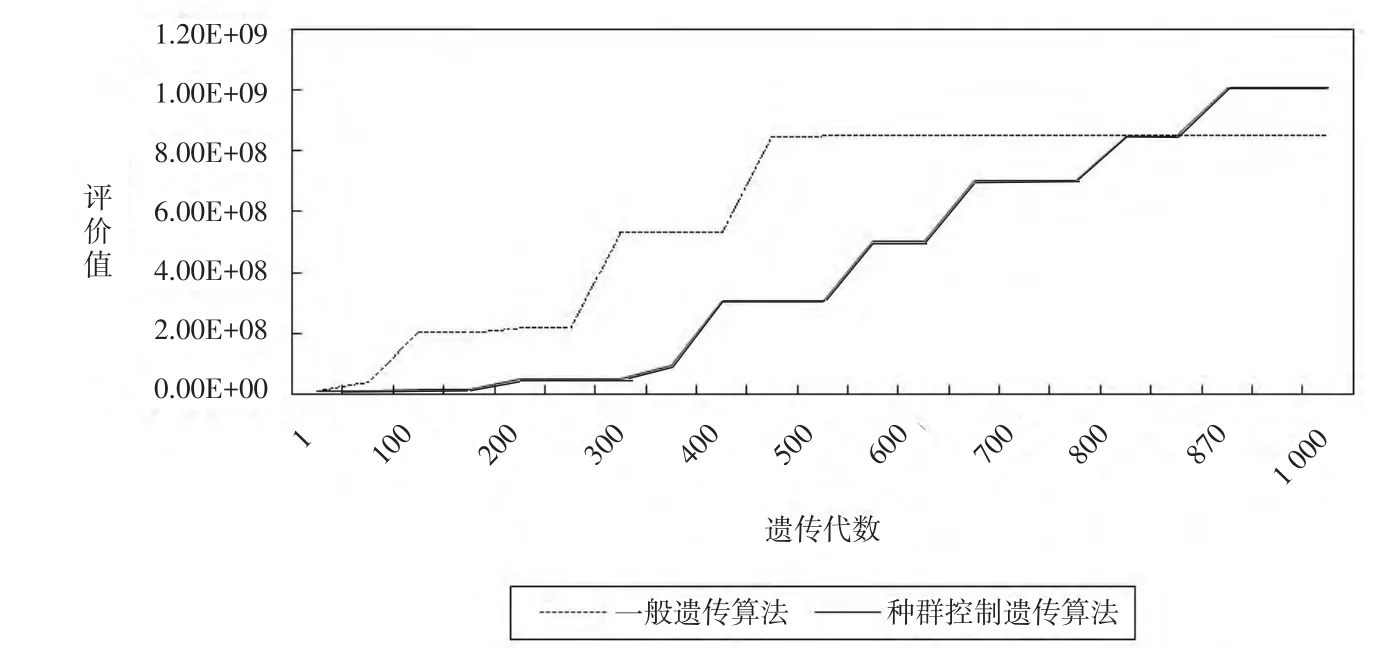
图7 两种算法收敛性对比Fig.7 Comparison of two algorithms convergence

按出行目的划分，到达同一商业点的出行者选择每个停车场的人数如表5所示.例如到商业点II上班的出行者共有45人，选择在新建车库地点2和8停车的人最多，各有7人，而各有4人选择新建车库地点5和7，是最少的.从表5停车总数统计一栏不难看出，选择在新建车库地点的出行者人数与该地所建车库规模正相关，即车库规模越大吸引的出行者越多.但车库利用率却正好相反，规模最大的三个车库地点2，6和8的利用率最高为83.5%，规模最小的三个车库地点4，5和7的利用率基本为95%，中间规模的二个车库利用率则接近95%.

表5 停车需求分配方案Table 5 The distribution of parking demand

每个新建立体车库的收费标准如表6所示，总利润为100396.6万元，其中停车收费为104336.6万元，修建车库成本为3940万元，包括固定成本115万元和可变成本3825万元.我们看到，吸引较多出行者的地点2，6和8收费反而最低，都不超过25元/小时辆，而其余地点收费则较高，地点4和5达到了上限30元/小时辆.由此我们得出一个规律：收费与停车数之间存在相反的关系，即收费越低，停车数越多.这与薄利多销的营销策略相吻合，而为收回成本，停车数少的车库只能采取提高收费单价的办法.

表6 收费方案Table 6 Charging scheme

5 研究结论

立体车库是解决城市尤其是商业中心区停车难的一个重要手段，车库规划应根据区域商业布局特点和出行需求做到统筹规划.本文建立的综合优化模型为车库选址、建设规模和收费标准的合理决策提供了科学依据.本文提出的控制种群多样性的遗传算法，通过调节可行解与不可行解子种群的规模，保留较优个体淘汰较差个体，维持种群多样性，克服了一般遗传算法早熟的缺陷.算例表明了模型和算法的正确性和实用性.

本文尚存在一些不足之处，如收费标准的制定比较单一，没有针对不同出行目的人群进行细分，比如可以对上班族实行月卡制度，实行一定的优惠；商业点的划分是人为确定的，尚缺乏定量依据.商业点的数量和位置划分是车库选址的前提，对决策有很大影响，过细不利于计算，过粗又失去意义.这些将是我们下一步要进行研究的内容.

[1]中华人民共和国国家统计局.2012年国民经济和社会发展统计公报,(2013-2-22)[2013-6-20].http://www.stats.gov.cn/tjgb/ndtjgb/qgndtjgb/t20130221_402874525.htm.[National Bureau of Statistics of China.Statistical Communique of the People's Republic of Chi⁃na National Economic and Social Development in 2012,(2013-2-22)[2013-6-20].http://www.stats.gov.cn/tjgb/ndtjgb/qgndtjgb/t20130221_402874525.htm.]

[2]《中国城市发展报告》编委会.中国城市发展报告(2011)[M].北京：中国城市出版社,2012.[“Urban De⁃velopment Report in China”Editorial Board.Urban De⁃velopment Report in China(2011)[M].Beijing:China City Press,2012.]

[3]Aros-Vera F,Marianov V,Mitchell J E.P-Hub ap⁃proach for the optimal park-and-ride facility location problem[J].European Journal of Operational Research,2013,226(2):277-285.

[4]Tang J X,Tang L X,Wang X P.Solution method for the location planning problem of logistics park with variable capacity[J].Computers&Operations Research,2013,40(1):406-417.

[5]牛国鹏,李建国,蒋兆远.基于粗糙集的立体停车库选址决策研究[J].兰州交通大学学报,2008,27(4):87-89.[NIU G P,LI J G,JIANG Z Y.Study on location decision of solid garage based on rough set[J].Journal of Lanzhou Jiaotong University,2008,27(4):87-89.]

[6]汤旻安,任恩恩,闫军,等.以兰州市为例的城市中心区立体车库选址分析及评价[J].兰州交通大学学报,2009,28(3):109-114.[TANG M A,REN E E,YAN J,et al.A study of site selecting analysis and evaluation of urban centers’shared mechanical parking garage in Lanzhou[J].Journal of Lanzhou Jiaotong University,2009,28(3):109-114.]

[7]梅振宇,陈峻,王炜.城市路内停车设置规模非线性优化模型及其算法[J].交通运输工程学报,2007,7(2):89-93.[MEI Z Y,CHEN J,WANG W.Nonlinear opti⁃mization model and algorithm of urban curb parking set⁃ting scale[J].Journal of Traffic and Transportation Engi⁃neering,2007,7(2):89-93.]

[8]MEI Z Y,XIANG Y Q,CHEN J,et al.Optimizing model of curb parking pricing based on parking choice behavior[J].Journal of Transportation Systems Engineering and Information Technology,2010,10(1):99-104.

[9]Hensher D A,King J.Parking demand and responsive⁃ness to supply,pricing and location in the Sydney cen⁃tral business district[J].Transportation Research Part A,2001,35(3):177-196.

[10] 郑士源.信息不完全时公共停车场停车费和规模优化[J].交通运输工程学报,2010,10(5):81-89.[ZHENG S Y.Parking fee and scale optimization of pub⁃lic parking lot with incomplete information[J].Journal of Traffic and Transportation Engineering,2010,10(5):81-89.]

[11]段刚,李引珍,田丽娜.基于技术站中转作业的集装箱空箱动态调运优化模型与算法[J].交通运输系统工程与信息,2012,12(2):111-118.[DUAN G,LI Y Z,TIAN L N.Dynamic empty container allocation model and algorithm based on technique station transfer opera⁃tion[J].Journal of Transportation Systems Engineering and Information Technology,2012,12(2):111-118.]