基于SLRF2005全球板块运动参数的求解

李春晓，李语强，熊耀恒

(1.中国科学院云南天文台，云南 昆明 650011；2.中国科学院大学，北京 100049)

基于SLRF2005全球板块运动参数的求解

李春晓1，2，李语强1，熊耀恒1

(1.中国科学院云南天文台，云南 昆明 650011；2.中国科学院大学，北京 100049)

基于由卫星激光测距(Satellite Laser Ranging，SLR)资料建立的国际地球参考架SLRF2005，利用SLR测站的坐标和速度场解算了全球5大板块的运动参数，并与地质模型NNR-NUVEL-1A作比较和分析，结果表明基于现代空间测量技术的欧拉极与地质模型基本一致，说明近几百万年板块的运动是稳定的，同时数据显示两者之间仍存在一定差异。

激光测距；板块运动；空间大地测量

CN53－1189/P ISSN1672－7673

20世纪70年代末美国航空航天局(National Aeronautics and Space Administration，NASA)最先发起了地壳动力学计划旨在用空间测地技术测量板块的运动，随后基于卫星激光测距数据的圣安德烈亚斯断层实验(SAFE)对空间大地测量技术探测地壳形变进行了首次尝试。文[1]作者通过分析1979－1982年的Lageos卫星资料计算了卫星激光测距测站之间的34个基线变化率，计算结果与Minster和Jordan建立的地质模型表现出总体的一致性，两者之间的线性交叉相关系数为0.61。文[2]作者则利用1978－1988年的Lageos测距资料对分布于全球7大板块的22个跟踪站的基线变化率进行了估计，结果与NUVEL-1模型表现出良好的一致性且两者之间的相关系数高达0.989，另外尺度上的微小差异可能是由最近站间基线速率的变化和地质时间尺度的不确定性引起的。文[3]作者联合全球SLR和VLBI数据求解了全球4大板块的欧拉极，结果表明基于空间技术的欧拉矢量的旋转速率普遍小于NUVEL-1模型下的转动速率。文[4]作者利用41个卫星激光测距测站的速度场对全球5大板块的欧拉极进行解算，并与地质板块模型RM-2和NUVEL-1作出比较，同时还分析了各板块上卫星激光测距站的局部形变特征。文[5]作者利用8年的Ajisai测距资料估计了卫星激光测距测站的速度并与之前Lageos的解算结果作出一致性检验。

在过去的十几年里，伴随着软件系统的提高和处理方法的改善，无论是在数据的覆盖范围，还是在数据的精度和质量上，空间大地测量技术一直在不断地发展，这主要包括甚长基线干涉(VLBI)、卫星激光测距(SLR)、全球定位系统(GPS)、多普勒定轨和卫星无线电定位(DORIS)等技术。由单一的空间大地测量建立的坐标架存在一定的局限性，这主要表现在测量技术的系统误差上。微波技术(GPS和DORIS)和VLBI受对流层的影响比较敏感，全球定位系统在模拟天线相位中心变化的过程中存在局限性，甚长基线干涉是获取地球定向的重要技术手段，但只能局限在相对位置的测量上，卫星激光测距对地球质心的变化是最敏感的并且对尺度的测定起着重要作用，但测站在全球的不均匀分布和测距资料的相对稀少以及可能存在的距离偏差限定了SLRF的精度[6]。

近几年随着空间大地测量技术的不断发展，卫星激光测距精度得到了进一步提高，同时全球范围内测站数量也随之增加以及测站的几何分布合理性也在逐渐改善，这使得基于激光测距数据建立起来的参考架成为可能。SLRF2005是通过结合ITRF2000和ITFR2005以及从1993－2007年的全球测距资料而建立的参考框架，该参考架包含了全球154个卫星激光测距站点，其中大部分测站位于欧亚板块和北美板块。

全球的卫星激光测距测站共分布于8个板块，其中阿拉伯板块(ARAB)上共有两个测站，而测站7530位于ARAB与AFRC的交界地带；纳兹卡板块(NAZC)上只有一个测站7097，而南美板块(SOAM)上的测站都位于NAZC与SOAM板块的交界区域，存在明显的区域性地壳形变。根据上述情况，本文利用了SLRF2005参考架下测站在历元2 000.0的速度场对AFRC(非洲板块)、AUST(澳大利亚板块)、EURA(欧亚板块)、NOAM(北美板块)、PCFC(太平洋板块)等5个板块的运动参数进行求解，并与地质模型进行比较，结果表明用激光测距求解的现时板块运动欧拉极与基于几百万年地球物理资料的NNR-NUVEL-1A模型的欧拉矢量基本一致，说明几百万年以来板块的运动是稳定的。

1 测站的筛选

测站筛选在求解板块运动参数的过程中起着至关重要的作用，如何进行测站的选择将直接影响得出的结论。本文对测站的筛选遵循以下3个原则[7]:(1)剔除位于板块边界及板内构造形变区域的测站；(2)剔除速度场精度低于2 mm/yr的测站；(3)通过与NNR-NUVEL-1A模型进行7参数拟合，按残差小于1个中误差的原则进行测站的筛选。

位于构造形变区域的测站将会对筛选结果产生很大影响，这直接关系到欧拉矢量的正确与否，例如位于北美板块与欧亚板块交界地区的几个日本测站(7308、7328、7335、7337、7339)直接导致所求解的欧拉极相对于地质模型产生较大的偏移，主要原因是位于环太平洋火山地震带的这几个测站的速度场精度均在2 mm/yr以上，而测站的权重是由速度场精度决定的，从而导致用加权最小二乘平差时，测站占有很大权重，单独用7参数拟合很难剔除这些测站，所以会出现错误的结果。文[8]作者利用Lageos测地卫星连续4年以上的跟踪数据对地中海地区的测站运动做出分析，其研究结果支持了阿拉伯板块相对于欧亚板块的北向运动，土耳其境内沿东北方向安那托利亚的滑动断层以及爱琴海盆地的拉伸，同时位于意大利和法国南部的几个测站的运动表现出局部形变与这些测站位于欧亚板块和非洲板块的交界地带是一致的。测站距离边界多远才算是靠近板块边界至今没有确切的标准，文[9]作者提出不需要确定板块边界和速度场精度，直接利用7参数变换通过1σ原则筛选VLBI测站的统计方法，随后文[10]作者利用ITRF2000下的GPS和VLBI测站通过7参数变换进行了测站的筛选。

对于速度场精度的选取也要视所用参考框架以及相关测量技术综合决定，目前ITRF2008、ITFR2005在精度上都较以前的参考架有了进一步提高，本文结合SLRF2005参考架，按照尽量保留大部分测站的原则选取速度场精度优于2 mm/yr作为筛选标准。

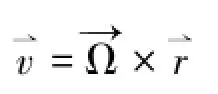
7参数变换实现了两种参考框架之间的坐标变换，同时通过两个参考框架之间的速度场变换可以得到7个参数的变化率，也即两个参考架需要用14个拟合参数统一。本文主要用了两个参考框架下测站的速度场资料，因此所拟合的7个参数应为变化率。两个参考架之间的变换方程[11]为:

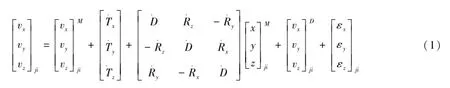
(1)式左边为SLRF2005参考架下板块j上测站i的速度场，右边依次为NNR-NUVEL-1A模型下测站的速度场、3个平移参数的变化率、矩阵由一个尺度因子D的变化率和3个旋转参数的变化率组成，最后两项分别为测站由局部形变引起的速度项和测量误差项。因为所选的测站要满足远离构造形变区域的要求，因此上式中由局部形变引起的速度相对于测站的刚性运动为小量，在满足一定精度的情况下可以忽略该项。为了方便计算将上式简化为矩阵形式，并利用最小二乘法拟合出7个参数。

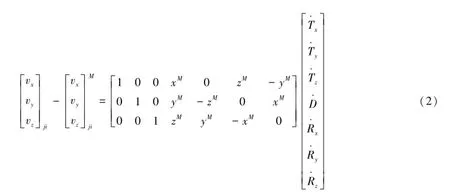
从(2)式可以看出要拟合出7个参数至少需要3个测站，对于参考框架下的测站坐标及速度场可直接从国际激光测距网和国际地球参考架等相关网站获取。对应于模型的测站坐标可以根据WGS84定义的参考椭球进行解算，若已知测站的地表纬度φ和经度θ以及高程H，通过下面的计算公式即可求出测站在该参考系下三维笛卡尔坐标。

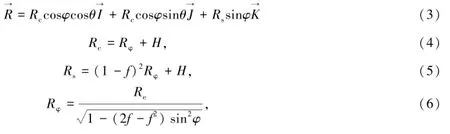
式中，f为参考椭球的扁率；Re为椭球的半长径。速度场可由欧拉运动定律得到，即:

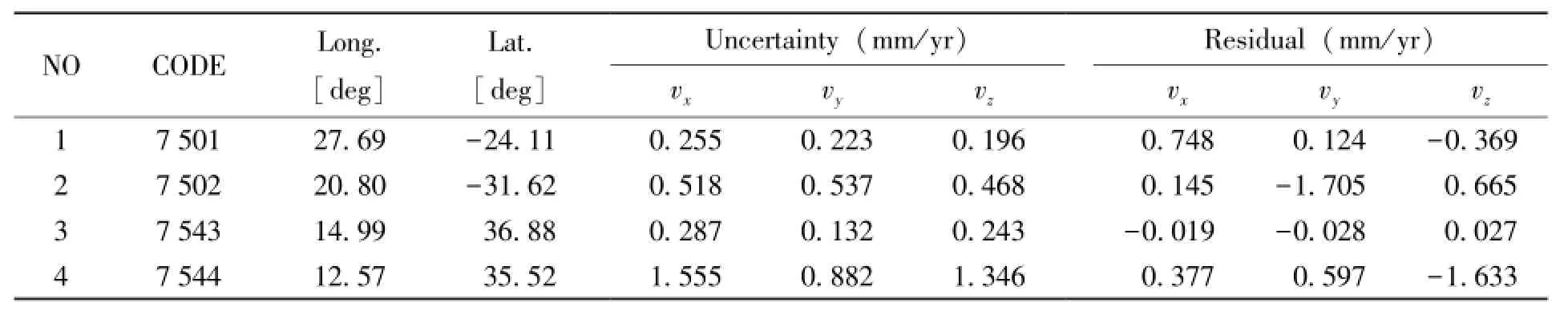
表1 非洲板块(AFRC)保留的测站及残差Table 1 Information about retained stations on the African plate(AFRC) and measurement error residuals of plate motions there

表2 澳洲板块(AUST)保留的测站及残差Table 2 Information about retained stations on the Australian plate(AUST) and measurement error residuals of plate motions there

2 板块运动参数的求解

基于板块是围绕通过地球质心的欧拉矢量作旋转运动的假设，测站的运动主要是沿球面运动，通常由冰期后地壳回弹引起的测站沿水平方向的速度项为小量，因此这部分水平运动可以忽略，同时前面已经筛选出位于板块稳定区域的测站，所以区域性地壳形变引起的测站水平速度场的变化量可以不予考虑。

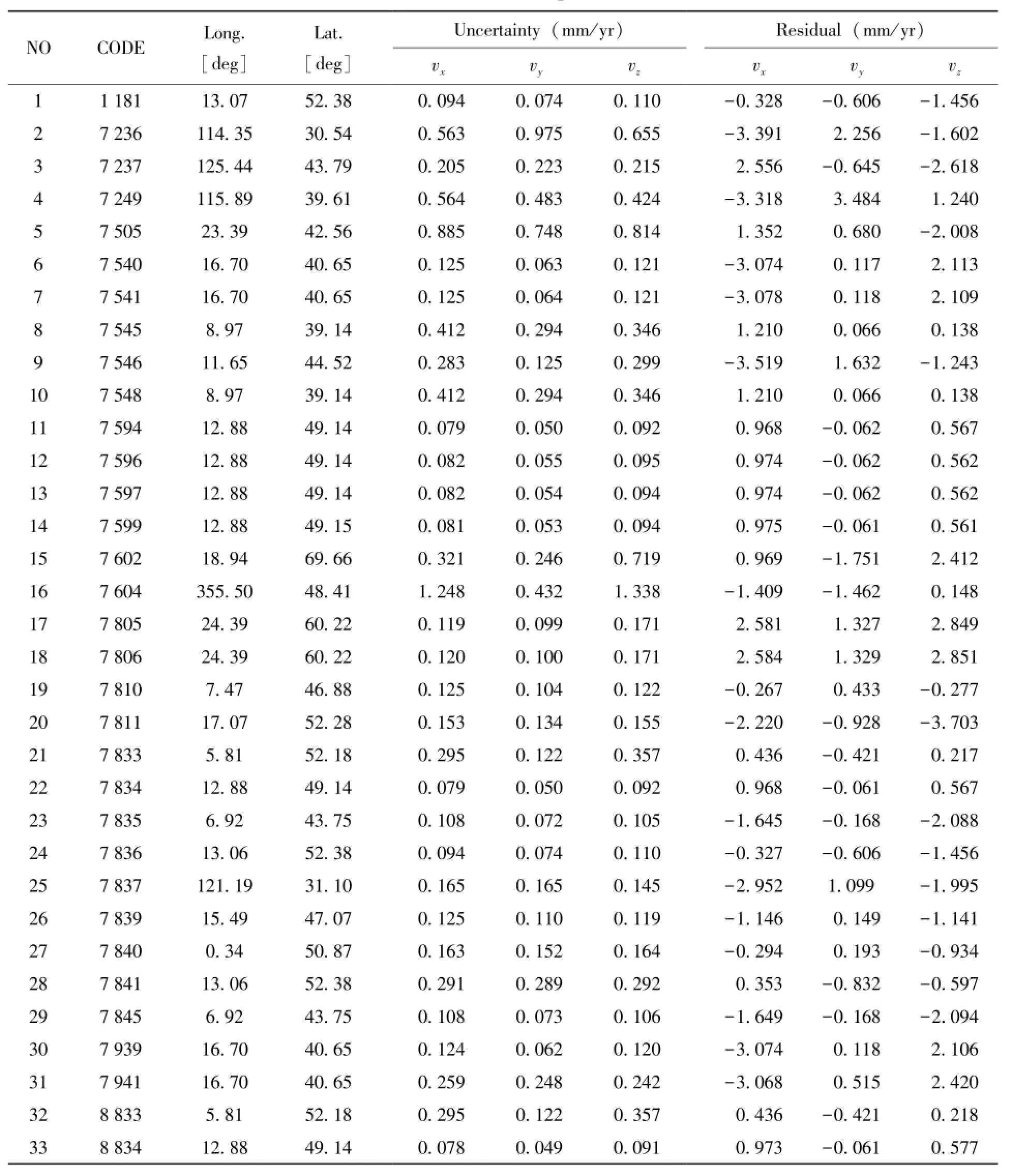
表3 欧亚板块(EURA)保留的测站及残差Table 3 Information about retained stations on the Eurasian plate(EURA) and measurement error residuals of plate motions there

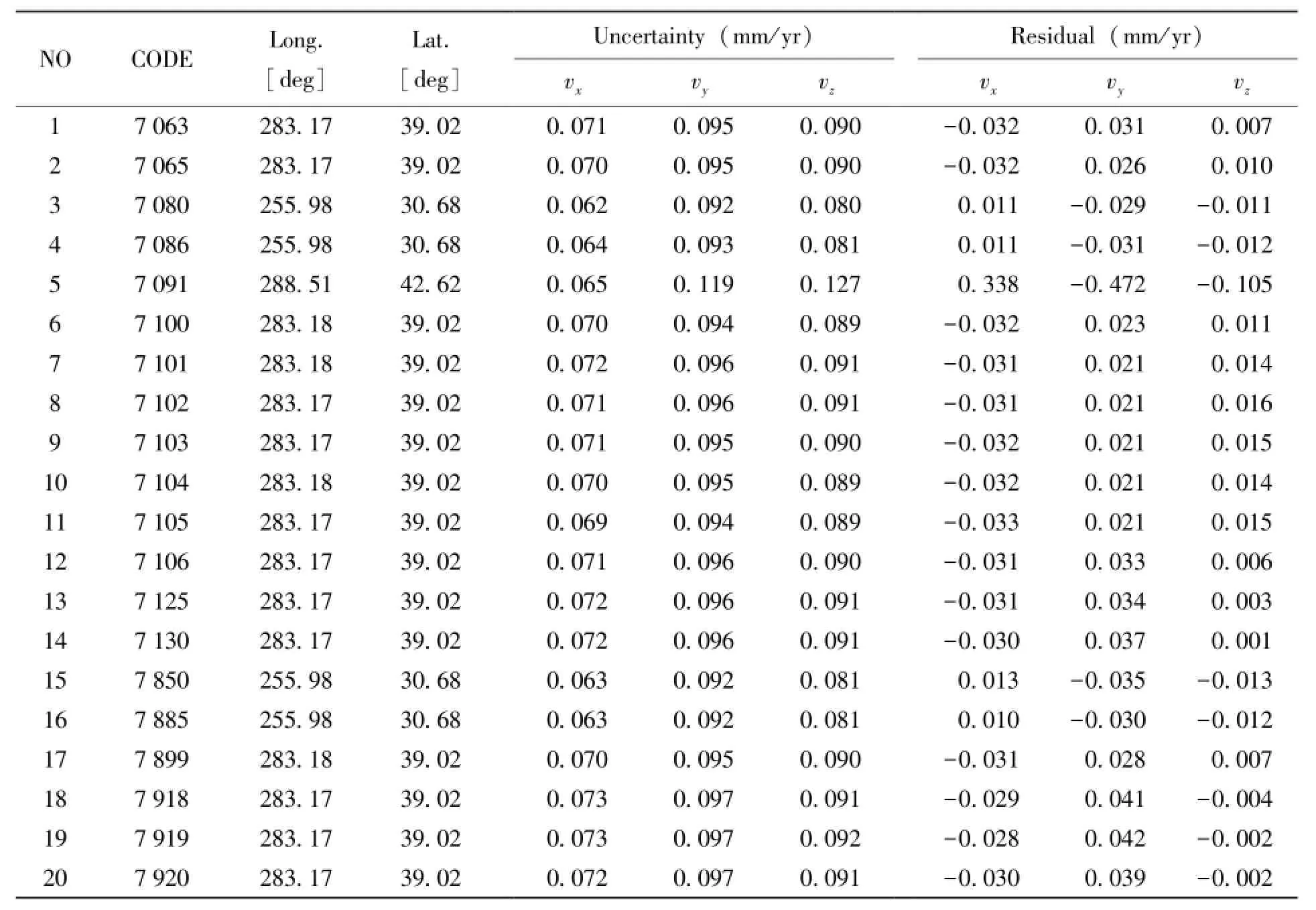
表4 北美板块(NOAM)保留的测站及残差Table 4 Information about retained stations on the North American plate(NOAM) and measurement error residuals of plate motions there

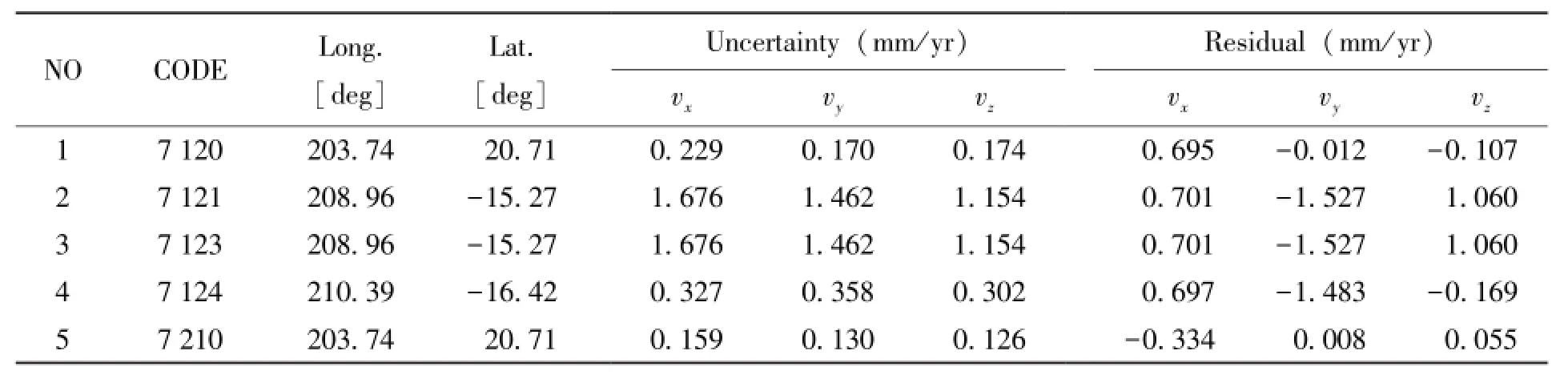
表5 太平洋板块(PCFC)保留的测站及残差Table 5 Information about retained stations on the Pacific plate(PCFC) and measurement error residuals of plate motions there

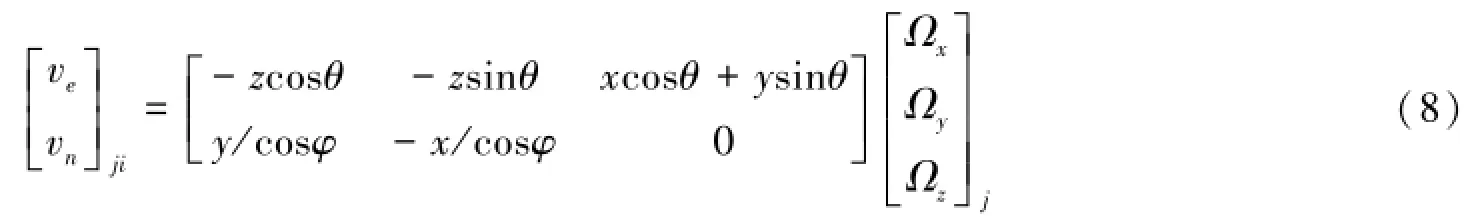
式中，ve、vn分别为测站j沿东向和北向的速度；θ、φ分别为测站j的经度和纬度，Ωx、Ωy、Ωz分别为板块i的欧拉极分量。为了便于比较，将欧拉矢量的直角坐标分量转换为球面坐标形式，有:

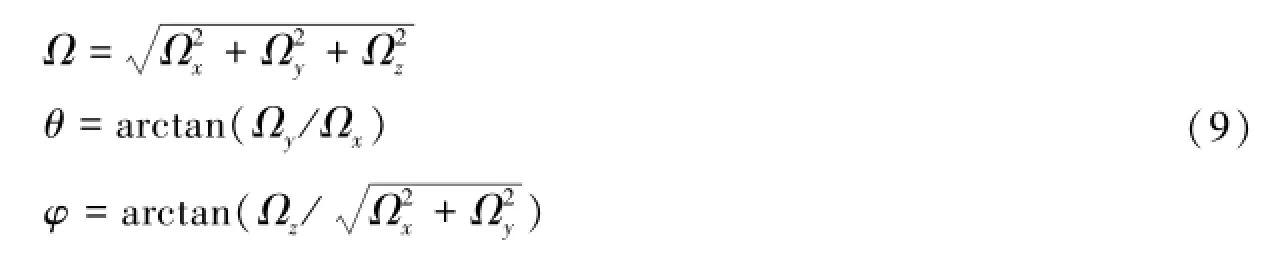
其相应的中误差可以用误差传递公式计算:

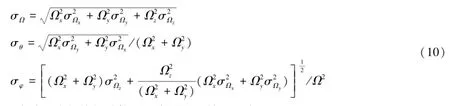
通过上述方法，计算了全球5个板块的欧拉极和中误差，结果见表6。

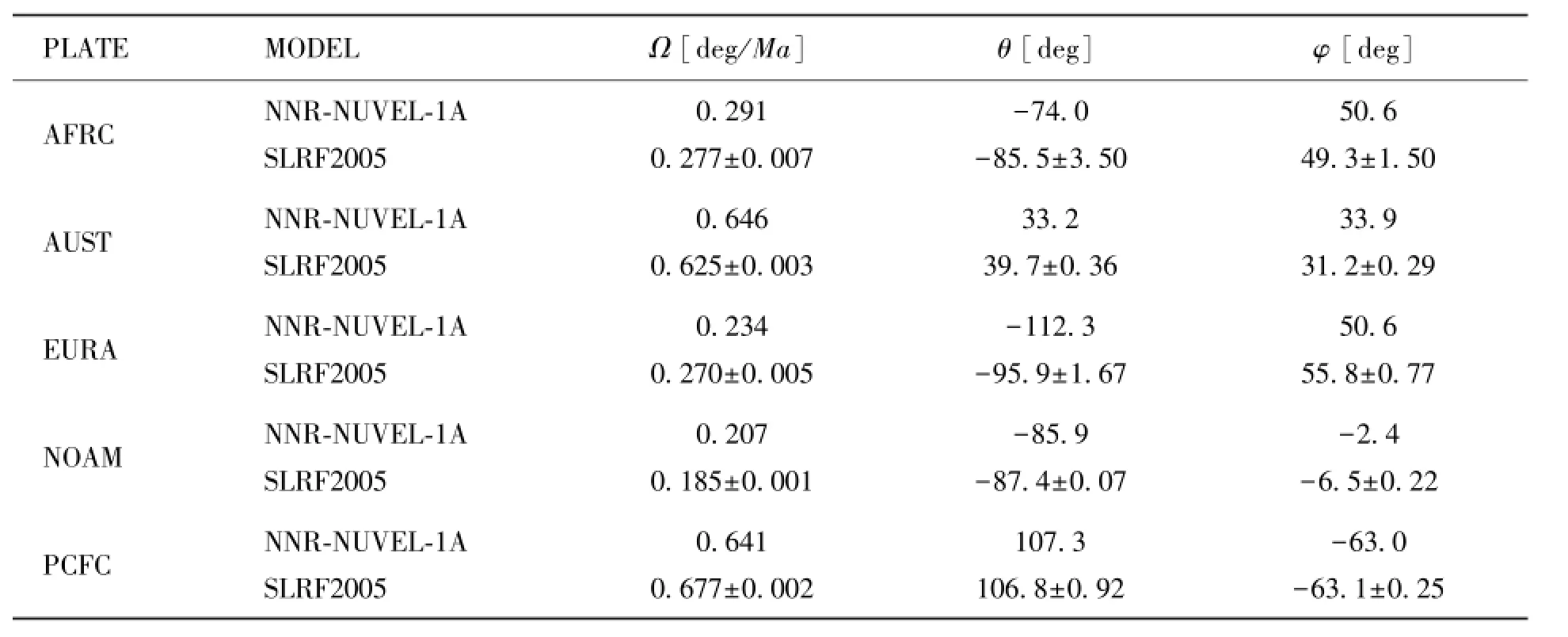
表6 全球5大板块的欧拉极及中误差Table 6 Derived parameters of Euler vectors and their rms errors for the five continental plates

3 讨 论

基于SLRF2005参考架下的测站速度场，利用7个参数变换使其向地质模型逼近，解算出全球5大板块的运动参数，从表6可以看出用现代空间测量技术解算的近几十年的板块运动参数与地质模型NNR-NUVEL-1A有较好的一致性，说明几百万年以来板块的运动是稳定的。同时两者之间存在一定的差异，其原因有如下几种:NNR-NUVEL-1A模型反映的是板块在几百万年内的平均运动，而近几十年板块的运动存在非线性因素，相对于百万年尺度反映了短期内板块的平均运动；测站在筛选过程中存在不确定性也会给欧拉极的求解带来一定影响，如测站到板块边界距离的不确定性，测站速度场精度选择的不确定性等；SLRF2005参考架的测站分布不均匀也会引起所求欧拉极的偏移，如欧亚板块上的测站大部分集中在欧洲，北美板块上的测站大都集中在北美大陆，因北美板块上的几个日本测站处于板块交界地带，测站剔除后导致测站的几何分布不均。由单一激光测距资料建立的国际地球参考架与由多种空间大地测量技术建立的ITRF2005之间的差异也会导致欧拉矢量的偏移，即不同的参考架会得到不同的结果。

随着ITRF2013即将建立，测站的精度不断提高，无论全球测站的数量还是几何分布都会比之前的参考架有进一步的提升，由此解算的欧拉极会更加精确以完善当今的板块运动模型。

[1] Christodoulidis D C，Smith D E，Kolenkiewicz R，et al.Observing tectonic plate motions and deformations from satellite laser ranging[J].Journal of Geophysical Research:Solid Earth，1985，90(B11):9249－9263.

[2] Smith D E，Kolenkiewicz R，Dunn P J，et al.Tectonic motion and deformation from satellitelaser ranging to LAGEOS[J].Journal of Geophysical Research:Solid Earth，1990，95(B13): 22013－22041.

[3] Robaudo S，Harrison C G A.Plate tectonics from SLR and VLBI global data[J].Geodynamics Series，1993，23:51－71.

[4] 孙付平，赵铭.全球5大板块的运动和形变－用卫星激光测距数据导出的站速度分析[J].地球物理学报，1994，37(5):596－605.

Sun Fuping，Zhao Ming.Study of plate motion and crustal deformation from satellite laser ranging site velocities[J].Acta Geophysica Sinica，1994，37(5):596－605.

[5] Sengoku A.A plate motion study using Ajisai SLR data[J].Earth Planets Space，1998，50: 611－627.

[6] Angermann D，Gerstl M，Kelm R，et al.Time evolution of an SLR reference frame[J].Advances in Space Research，2002，30(2):201－206.

[7] 柴洪州，明锋，段婷婷，等.全球板块运动背景场及ITRF2005VEL的建立[J].测绘科学技术学报，2009，26(2):79－85.

Chai Hongzhou，Ming Feng，Duan Tingting，et al.Establishing of background field of global plate motion and ITRF2005VEL[J].Journal of Geomatics Science and Technology，2009，26 (2):79－85.

[8] Noomen R，Ambrosius B A C，Wakker K F.Crustal motions in the Mediterranean Region determined from Laser ranging to LAGEOS[J].Geodynamics Series，1993，23:331－346.

[9] Li Jinling，Zhang Bo，Zhao Ming，et al.A statistical selection of on-plate sites based on a VLBI global solution[J].Earth Planets Space，2001，53:1111－1119.

[10] 金双根，朱文耀.确定板块运动学模型的台站选取[J].大地测量与地球动力学，2003，23 (3):56－60.

Jin Shuanggen，Zhu Wenyao.Choice of stations for kinematic plate model[J].Journal of Geodesy and Geodynamics，2003，23(3):56－60.

[11] Altamimi Z，Collilieux X，Legrand J，et al.ITRF2005:A new release of the international terrestrial reference frame based on time series of station positions and Earth orientation parameters[J].Journal of Geophysical Research:Solid Earth，2007，112(B9):B09401.

[12] 叶叔华.天文地球动力学[M].济南:山东科学技术出版社，2000:300－301.

Parameters of Global Plate Motions based on the SLRF2005

Li Chunxiao1，2，Li Yuqiang1，Xiong Yaoheng1
(1.Yunnan Observatories，Chinese Academy of Sciences，Kunming 650011，China，Email:lcx＠ynao.ac.cn；2.University of Chinese Academy of Sciences，Beijing 100049，China)

We solve parameters of motions of the five continental plates(i.e.，Pacific Plate，Australian Plate，African Plate，Eurasian Plate，and the North American plate)with Satellite Laser Ranging(SLR) station coordinates and measured velocity fields based on the SLRF2005.The SLRF2005 was established using global SLR data.We compare our results to the geological model NNR-NUVEL-1A and find that the Euler vectors according to measurements with modern space technologies agree precisely with those given by the geological model.This indicates that plate motions have been stable in millions of years.However，there are small yet noticeable differences between the Euler vectors evaluated from the two sources.

Satellite Laser Ranging；Plate Motions；Space geodetic measurement

P3

A

1672－7673(2014)02－0127－07

2013－04－28，

2013－05－28

李春晓，男，硕士.研究方向:全球板块运动.Email:lcx＠ynao.ac.cn