偏心受压风力机基础的倾斜计算

杨丽，韩彦宝

（北京木联能工程科技有限公司，北京 100096）

《FD003—2007风电机组地基基础设计规定（试行）》规定倾斜率系指基础倾斜方向实际受压区域两边缘的沉降差与其距离的比值。风力机基础受风荷载作用或土层不均匀的影响偏心受压，会产生倾斜。基础的倾斜对风力机上部结构会产生不利影响，造成后果很难处理，纠偏困难。规范中要求计算风力机基础的倾斜量，但未给出明确的计算方法，如何准确地计算风力机基础的倾斜成为风机设计人员急需解决的问题。本文以实际工程为例，给出偏心受压风力机基础正常运行工况及极端荷载工况下的倾斜计算的具体算法，希望能为广大风力机基础设计人员提供有益帮助。

1 计算公式

设计规范中规定倾斜率按下式计算：

式中，s1、s2为基础倾斜方向实际受压区域两边缘的最终沉降量，mm；bs为基础倾斜方向实际受压区域的宽度。

基础在偏心荷载作用下，基底压力分布图形有梯形分布和三角形分布，梯形分布时，基础未脱开，三角形分布时，基础部分脱开，但脱开的面积符合规范要求。

沉降量计算公式如下：

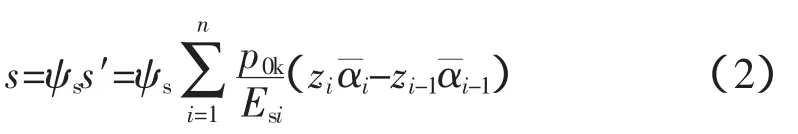
式中，s为地基最终沉降量；s′为按分层总和法计算出的地基沉降值；ψs为沉降计算经验系数，根据地区沉降观测资料及经验确定，无地区经验时可查与土层当量压缩模量Es有关的沉降计算经验系数表选用。

压缩模量计算公式为：

式中，Ai为第i层土附加应力系数沿土层厚度的积分值；Esi为扩展基础底面下第i层土的压缩模量，应取自自重压力至土的自重压力与附加压力之和的压力段计算；n为地基沉降计算深度范围内所划分的土层数；p0k为荷载效应标准组合下，扩展基础底面处的附加压力；αi、α軍i－1为扩展基础底面计算点至第i、i－1层土底面范围内平均附加应力系数，圆形扩展基础可参考《建筑桩基技术规范》2008附录D.0.3。

1.1 基底附加应力为梯形分布时s2和s1的计算

规定s2为基础边缘最大压力pmax所对应端点2的沉降量，s1为基础边缘最小压力pmin所对应端点1的沉降量。参考GB50135—2006《高耸结构设计规范》，可知

基底边缘处最大压力：

基底边缘处最小压力：

基底附加应力为梯形分布时，可将荷载分为均布荷载和三角形荷载两部分，分别计算其相应的沉降量再进行叠加，如图1所示。

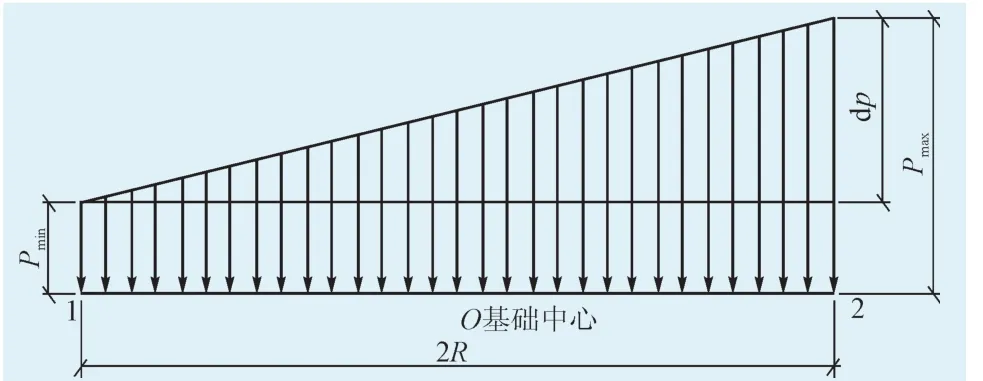
图1 梯形分布荷载作用下计算示意图Fig.1 Calculation diagram under the trapezoidal distribution load

由图1可以看出，均布荷载部分的沉降量计算的基底附加压力

三角形荷载部分的沉降量计算的基底附加压力

由此得出，端点2的合计沉降量=三角形分布的2点的沉降量+均布荷载部分的沉降量

同理，端点1的合计沉降量=三角形分布的1点的沉降量+均布荷载部分的沉降量

1.2 基底附加应力为三角形分布时s2和s1的计算

基底附加应力为三角形分布时，说明基础底面部分脱开，此时可将荷载换算为作用在整个基础宽度上的相似大三角形荷载和均布荷载两部分，分别计算其相应的沉降量再进行叠加，如图2所示。

基底边缘处最大压力

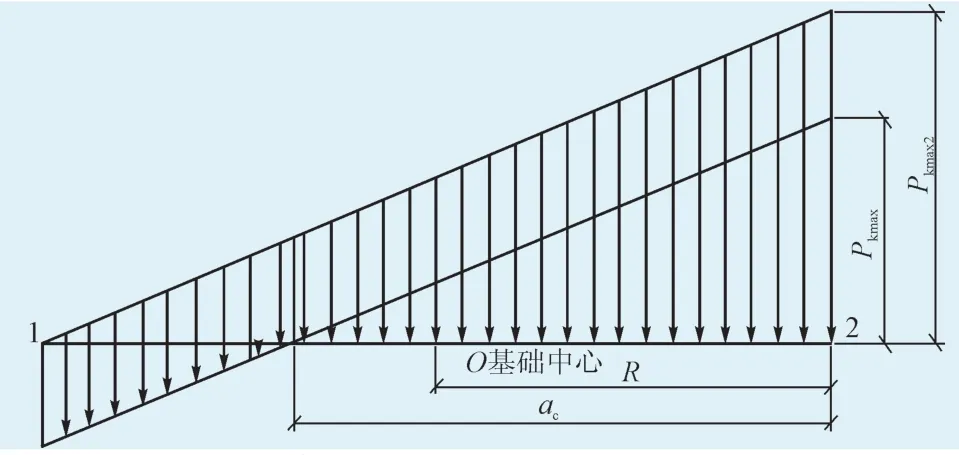
图2 三角形分布荷载作用下计算示意图Fig.2 Calculation diagram under the triangular distribution load

基底受压面积宽度

式中，ξ、τ为计算系数，根据e/R按《高耸结构设计规范》GB50135—2006附录C确定。

由几何关系推导可得，

由图2可以看出，均布荷载部分的沉降量计算的基底附加压力

三角形荷载部分的沉降量计算的基底附加压力

由此得出，端点2的合计沉降量=三角形分布的2点的沉降量-均布荷载部分的沉降量

同理，端点1的合计沉降量=三角形分布的1点的沉降量-均布荷载部分的沉降量。

2 工程实例

2.1 工程概况

某中型风电场，采用某厂家单机容量2.5 MW的风力发电机组，风轮直径106 m，轮毂高度80 m，50年极端风速52.5 m/s，风场类型为IECIII=3，上部结构传至塔筒底部的内力标准值见表1，地基土岩土力学参数见表2。

风电机组基础选用圆形扩展基础，安全等级为二级，基础底板半径R=10.6 m；基础底板外缘高度H1=1 m；基础棱台顶面半径R1=3.3 m；基础底板棱台高度H2=1.5 m；基础台柱半径R2=3.3 m；台柱高度H3=0.7 m；塔筒直径D=4.7 m；上部荷载作用力标高Hb=0.9 m；基础埋深Hd=3.1 m；地下水埋深Hw=10 m。

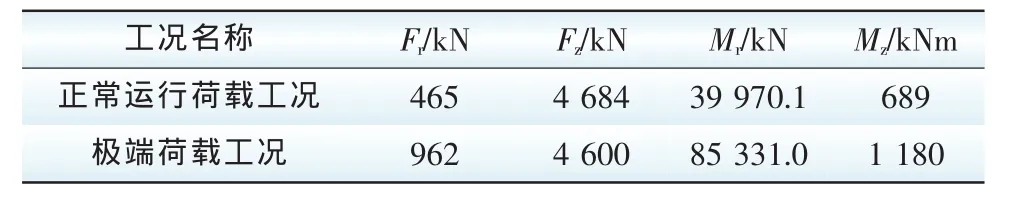
表1 上部结构传至塔筒底部的内力标准值Tab.1 Standard load from super structure to the tower bottom

表2 地基土岩土力学参数Tab.2 Mechanical parameters of rock and soil

2.2 倾斜计算

2.2.1 正常运行荷载工况

基础底面的抵抗矩计算公式

由式（13）可得：

偏心距计算公式

由式（14）可得：

根据《高耸结构设计规范》GB50135-2006中附录C，可知基础面积未脱开，基底压力分布图为梯形。

基底边缘处最大压力，由式（4）可得：

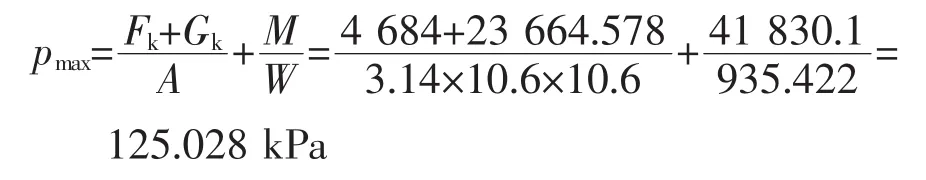
基底边缘处最小压力，由式（5）可得：

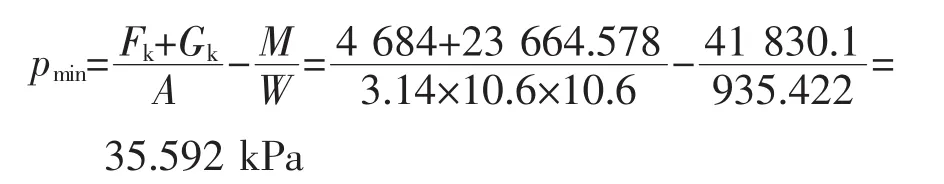
由倾斜计算的计算原理可知，基底附加应力为梯形分布时，可将荷载分为均布荷载和三角形荷载两部分，分别计算其相应的沉降量再进行叠加。

均布荷载部分的沉降量计算的附加压力，由式（6）可得：p0k=pmin=35.592 kPa；

三角形荷载部分的沉降量计算的附加压力，由式（7）可得：

p0k=pmax－pmin=125.028－35.592=89.436 kPa；均布荷载部分的沉降量计算结果见表3。

表3 均布荷载引起的沉降量计算表Tab.3 Settlement calculation table due to the uniform distribution load

z=13.3 m ～14.3 m，土层计算沉降量

由式（3）可得，

查《设计规定》中表8.4.3，p0k=35.592 kPa<0.75fak=0.75×140=105 kPa，

则由式（2）可得，采用内插法计算得到沉降计算经验系数ψs=0.7056。

均布荷载引起的最终的沉降量为：

s=ψss′=ψs∑Δs′i=0.7056×47.813=33.74 mm。

三角形分布荷载2点部分引起的沉降量计算结果见表4。

z=13.3 m至14.3 m，土层计算沉降量

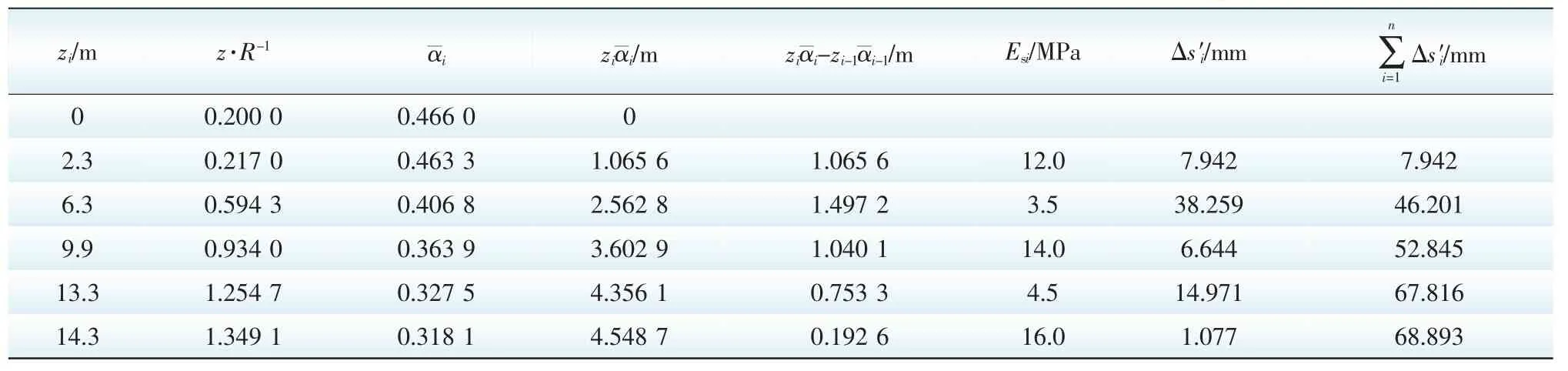
表4 三角形分布荷载2点部分引起的沉降量计算表Tab.4 Settlement calculation table due to triangular distribution load two points

由沉降计算深度范围内压缩模量的当量值E軍s可查表1得ψs系数

由式（3）可得：

查《设计规定》中表8.4.3，p0k=89.436 kPa<0.75fak=0.75×140 kPa=105 kPa，

则采用内插法计算得到沉降计算经验系数ψs=0.7077。

则由式（2）可得，三角形分布2点的荷载引起的最终沉降量为：

s=ψsψs∑Δ=0.7077×68.893 mm=48.76 mm。

同理，三角形分布荷载1点部分引起的沉降量计算结果见表5。

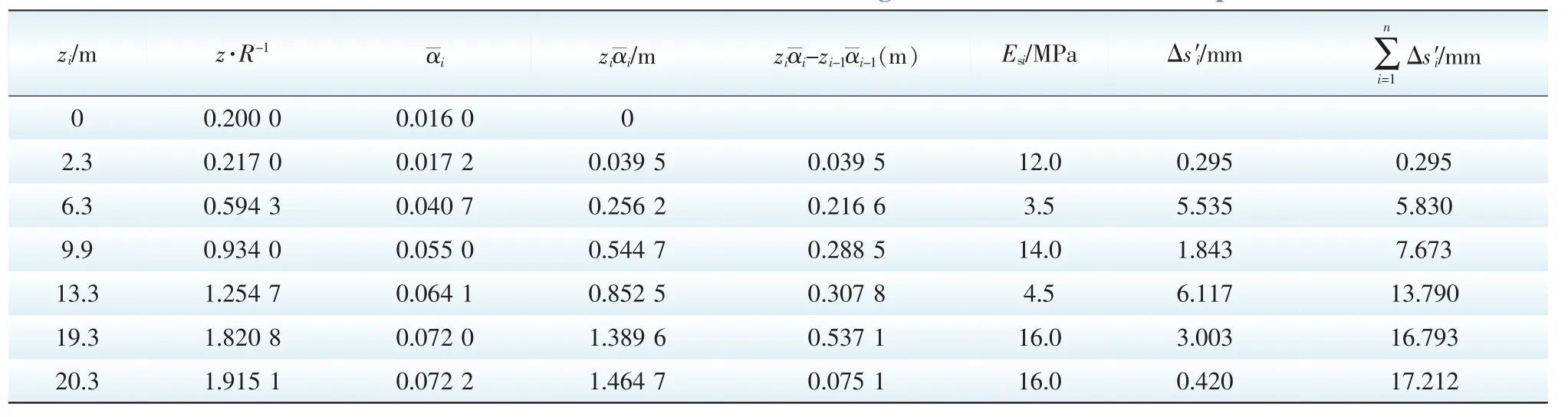
表5 三角形分布荷载1点部分引起的沉降量计算表Tab.5 Settlement calculation table due to triangular distribution load one point

z=19.3 m ～20.3 m，土层计算沉降量

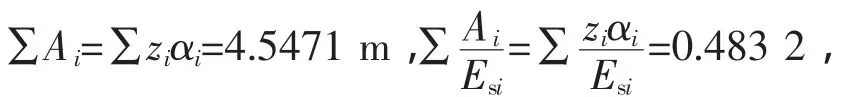
用内插法计算得沉降计算经验系数ψs=0.6096。

则由式（2）可得，三角形分布1点的荷载引起的最终沉降量为：

端点2的合计沉降量s2=48.76+33.74=82.5（mm）

端点1的合计沉降量s1=10.49+33.74=44.23（mm）

则由式（1）可得，正常运行荷载工况下基础的倾斜率为

2.2.2 极端荷载工况

根据《高耸结构设计规范》GB50135-2006中附录C，可知基础底已有脱开，脱开面积未超过全面积的1/4。基底附加压力为三角形分布时，可将荷载换算为作用在整个基础宽度上的相似大三角形荷载和均布荷载两部分，分别计算其相应的沉降量再进行叠加，得出倾斜率。

根据e/R的值查表C用内插法计算得基底压力计算系数τ=1.828，ξ=1.428，由式（9）可得，基底实际受压宽度ac=τR=1.828×10.6 m=19.376 m，由此可得出基础底面实际受压面积As=338.268 m2。

由式（8）可得，边缘处最大基底压力：

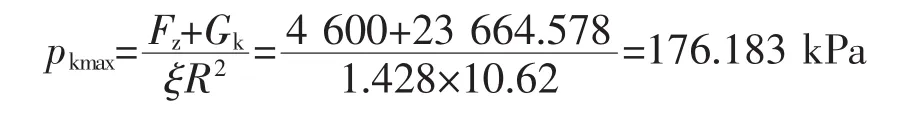
由式（11）可得，均布荷载部分沉降量计算的基底附加压力：

p0k=pkmax2－pkmax=192.763－176.183=16.580 kPa

由式（12）可得，三角形荷载部分沉降量计算的基底附加压力：

p0k=pkmax2=192.763 kPa

均布荷载部分的沉降量计算方法同正常工况下均布荷载的计算方法一致，结果如下：

均布荷载引起的最终的沉降量为：

s=ψss′=ψs∑Δs′i=0.7056×32.327=22.81 mm。

三角形分布荷载2点部分引起的沉降量计算方法同正常工况，结果如下：

三角形分布2点的荷载引起的最终沉降量为：

s=ψss′=ψs∑Δs′i=1.0077×148.486=149.63 mm。

同理，三角形分布荷载1点部分引起的沉降量计算结果为：

s=ψss′=ψs∑Δs′i=0.8192×37.098=30.39 mm。

综上可得，端点2的合计沉降量s2=149.63-22.81=126.82 mm

端点1的合计沉降量s1=30.39-22.81=7.58 mm

由式（1）可得，极端荷载工况下基础的倾斜率：

说明设置的基础底板半径偏小，需要调整，经试算当基础半径设计为11.3 m时，极端荷载工况下的倾斜率满足规范的要求，详细计算过程略。

3 结语

综上所述，该工程实例中，当风力机在正常运行荷载作用下，基础底面未脱开，基础倾斜率为0.002，小于规范值0.005，满足规范要求；当风力机在极端荷载作用下，基础底面部分脱开，基础倾斜率为0.0056，大于规范值0.005，不满足规范要求，需要调大基础底板的半径。从本文提供的偏心受压风力机基础倾斜计算方法来看，计算过程符合国家现行规范，计算原理简单，实用性较强，通过本文希望能为广大风电场风力机基础设计人员在计算基础变形方面提供有益帮助。

[1] 水利水电规划设计总院.FD003-2007风电机组地基基础设计规定（试行）[S].北京：中国水利水电出版社，2008.

[2] 中华人民共和国建设部，中华人民共和国国家质量监督检验检疫总局.GB50135-2006高耸结构设计规范[S].北京：中国计划出版社，2007.

[3] 中华人民共和国住房和城乡建设部.GB5007-2011建筑地基基础设计规范[S].北京：中国建筑工业出版社，2012.