同波束VLBI差分时延率研究

贺庆宝，刘庆会，郑 鑫，吴亚军，唐明乐

(1.中国科学院上海天文台，上海 200030；2.中国科学院大学，北京 100049)

同波束VLBI差分时延率研究

贺庆宝1，2，刘庆会1，郑 鑫1，2，吴亚军1，2，唐明乐1，2

(1.中国科学院上海天文台，上海 200030；2.中国科学院大学，北京 100049)

通过分析SELENE的两颗小卫星Rstar和Vstar的同波束VLBI数据，发现两卫星间差分时延率中由中性大气和电离层引起的长周期变化已被去除，且在小角距时，短周期变化也能绝大部分被去除。但角距离越大，去除部分越小。通过将2008年一年中8个台站组成的所有基线的相关相位拟合残差数据分别平滑积分30 s与60 s后，再通过5点直线拟合求得时延率，得出单卫星时延率随机误差分别约为0.32 ps/s RMS与0.20 ps/s RMS，而差分时延率随机误差分别为0.19 ps/s～0.32 ps/s RMS与0.09 ps/s～0.17 ps/s RMS。单卫星的时延率随机误差在秋季最大，春季最小，而差分时延率的随机误差在全年基本稳定。

VLBI；时延率；差分时延率；同波束

CN53－1189/P ISSN1672－7673

甚长基线干涉测量(Very Long Baseline Interferometry，VLBI)技术诞生于20世纪60年代后期[1]，具备高精度的测角能力，对与视线垂直方向上的轨道变化有较高灵敏度[2]。而传统的测速测距在视线方向上灵敏度较高，VLBI和测速测距的同时利用可以极大地提高深空探测器的测定轨精度[2]。我国的嫦娥一号与嫦娥二号卫星就是采用测速测距与VLBI的综合测量体制，共同完成月球卫星的定位定轨测量。利用VLBI系统对卫星进行测定轨主要是利用卫星的时延及时延率数据。目前利用单卫星的时延及时延率数据进行测定轨已经开展过很多研究，双卫星的差分时延数据也已被研究并利用到测定轨上，如日本的SELENE利用差分时延和测速测距数据把两颗小卫星的定轨精度提高至10 m[3]。但是双卫星间的同波束VLBI的差分时延率研究尚不深入，比如，差分时延率的随机误差在什么范围?比单卫星的时延率随机误差低多少?在多大角距离下能有效消除中性大气与电离层引起的误差?针对这些疑问，利用SELENE的数据进行了差分时延率的研究。

SELENE由3颗卫星组成，即绕100 km极轨圆轨道飞行的三轴稳定主卫星和绕椭圆轨道飞行的两颗自旋稳定的小卫星Rstar和Vstar[2，4－5]。两颗小卫星分别发送S频段的3个点频信号(f1，f2，f3)，频率分别为2 212、2 218、2 287 MHz[5]。在两卫星角距离小于0.56°时让天线主波束对准Rstar与Vstar的中间点进行跟踪观测[2]，角距离越大，天线接收的信号的信噪比越低。对其进行同波束观测的VLBI网主要包括日本国立天文台VERA的4个20 m观测站(水泽MZSW、入来IRIK、小笠原OGSW、石垣岛ISGK)以及中国上海(25 m)、乌鲁木齐(25 m)、澳大利亚Hobart(26 m)和德国Wettzell(20 m)4个观测站[6]。

利用任意一频点信号的相关相位都可求解时延率和差分时延率，本文利用f1频点进行求解，并分析了差分时延率在大角距与小角距(小于0.1°)情况下的差别。结果表明，在小角距时的差分时延率的随机误差远小于大角距时的差分时延率随机误差。其次，通过处理2008年一年中所有基线的数据，统计了在30 s、60 s积分时不同角距离情况下的单卫星时延率以及差分时延率的随机误差，并得出单卫星的时延率随机误差在秋季最大、春季最小，而差分时延率的随机误差在全年基本稳定的结论。

1 大角距与小角距的差分时延率比较

时延率是时延的时间微分，反映时延随时间变化的趋势。单卫星的时延率计算公式为:

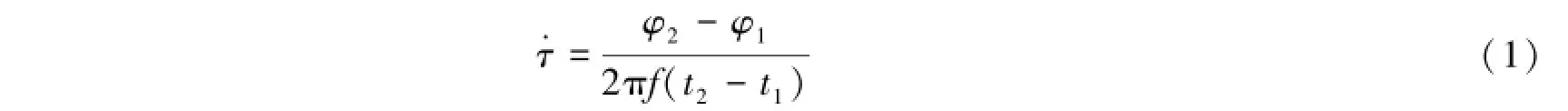
其中φ2、φ1分别是t2、t1时刻的相关相位；f是接收信号的频率。以SELENE为例，差分时延率的计算公式可写为:

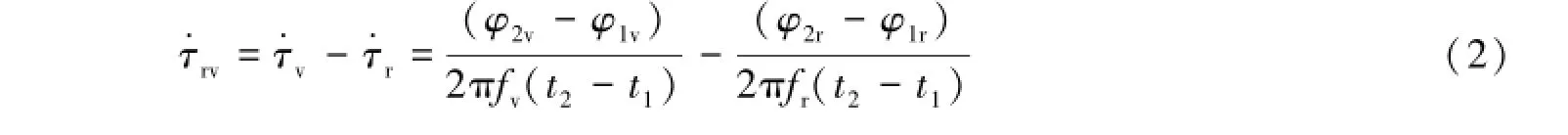
为了区别中性大气与电离层引起的长周期与短周期变化，对单卫星的时延率，先对每个弧段(约30 min)的f1频点的相关相位进行9次多项式拟合，然后对拟合相位与拟合残差相位分别求时延率，最后将Rstar与Vstar的时延率相减即得到差分时延率。同时，为了表明大角距与小角距时差分时延率的区别，随机选择了IRIK-OGSW基线在2008年5月23日一天中两个时段作比较。图1与图2分别反应大角距与小角距时段由中性大气和电离层引起的长周期变化。图1和图2中的时延率都是用前点相位减去后点相位再除以频率得到。在图1和图2的(c)图，可看到Rstar与Vstar由拟合相位得到的时延率的抖动比较相似，说明不管在大角距还是小角距时，两卫星发射的信号受中性大气与电离层的长周期变化影响一致，而它们的差分时延率能消除这种长周期变化的影响。由图1、2的(b)图可知，Rstar与Vstar的拟合相位残差的相似度在小角距时比大角距时要高得多。

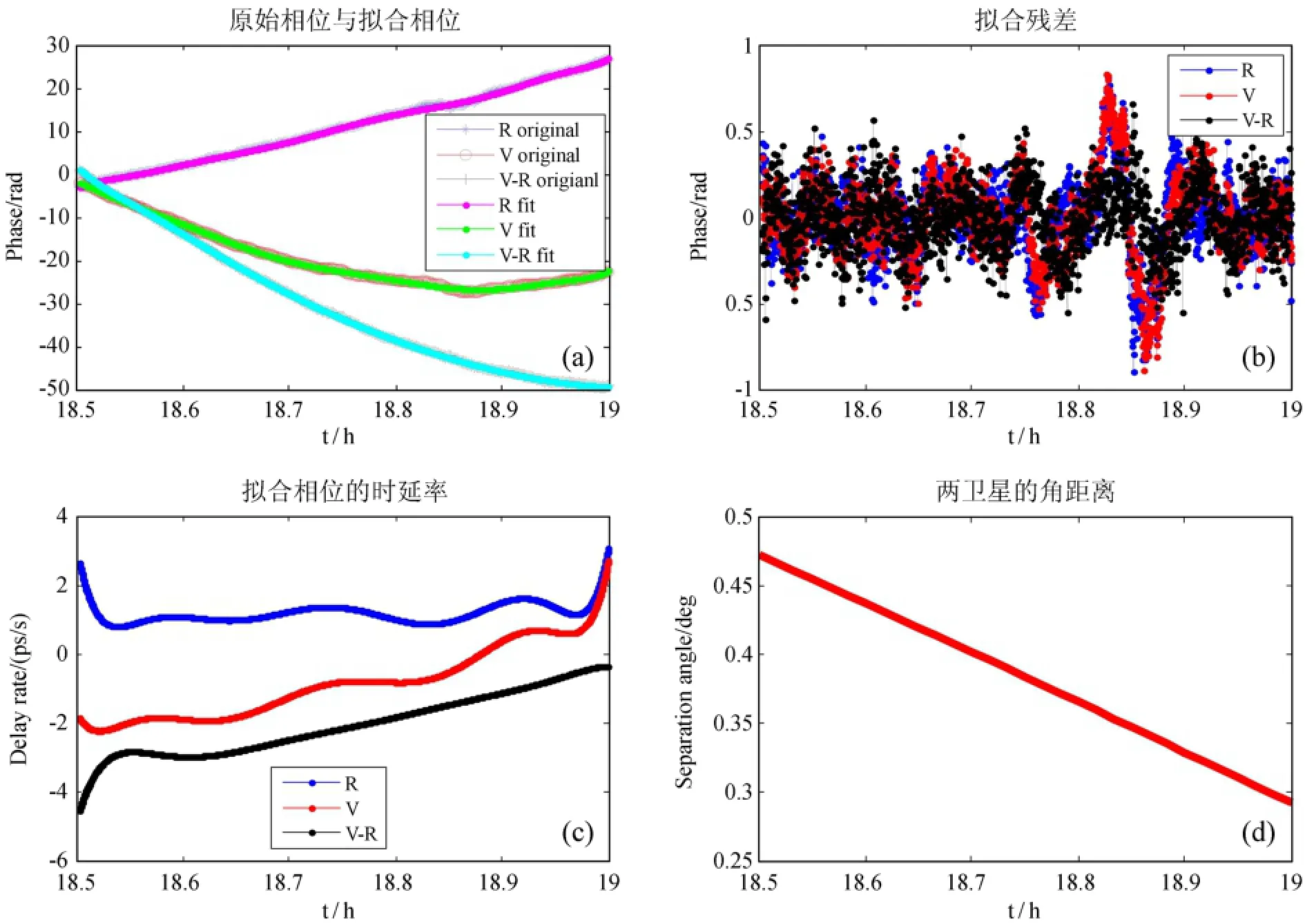
图1 大角距时的结果。(a)原始相关相位与拟合后的相关相位；(b)拟合相位残差；(c)用拟合相位求得的时延率与差分时延率；(d)两卫星的角距离Fig.1 Results for large separation angles between two satellites.(a)Correlation-phase data and fits to these.(b) Residuals of the correlation-phase data after subtracted by the fits.(c)Delay rates and difference delay rates obtained by using the fits of the correlation-phase data.(d)Separation angles

图2 小角距时的结果。(a)原始相关相位与拟合后的相关相位；(b)拟合相位残差；(c)用拟合相位求得的时延率与差分时延率；(d)两卫星的角距离Fig.2 Results for small separation angles between two satellites.(a)Correlation-phase data and fits to these.(b) Residuals of the correlation-phase data after subtracted by the fits.(c)Delay rates and difference delay rates obtained by using the fits of the correlation-phase data.(d)Separation angles

图3与图4分别是大角距和小角距时段由拟合相位残差通过5点直线拟合求得的时延率残差，分别反应大角距与小角距时段由中性大气与电离层引起的短周期变化。图3和图4中的时延率求解方法如下:先对拟合相位残差分别进行5 s、30 s、60 s、100 s的滑动平均，然后再用5点直线拟合法求Vstar和Rstar的时延率残差，及两卫星的差分时延率残差。

用拟合相位残差求得的单卫星的时延率残差包含有中性大气、电离层、观测装置、热噪声等影响。由于装置的影响在同一时刻对接收的两个卫星的信号几乎相同，所以差分时延率残差基本消除了装置的影响。在图3中，5 s积分时差分时延率残差的RMS值最大。其原因为在5 s积分时，单卫星时延率残差的热噪声影响较大，而差分时延率残差中的热噪声影响是单卫星时延率残差的2倍。再加上角距离较大时，两卫星的信号传播路径不同，中性大气与电离层对两卫星信号的影响不一致，差分处理并不能把它们消除。随着积分时间的增加，热噪声影响变小，使得差分时延率残差的RMS变为最小。尽管如此，在积分100 s时，差分时延率残差仍然有±0.4 ps/s的波动。图4中，由于是小角距时段，两卫星的信号传播路径相离较近，中性大气与电离层的影响基本一致，尽管差分时延率残差中噪声含量是单卫星时延率残差中的倍，但由于中性大气与电离层的影响绝大部分因差分处理而消除，使得差分时延率残差的RMS最小。在100 s积分时，差分时延率残差RMS值为0.05 ps/s，单卫星时延率残差RMS为0.38 ps/s，这充分显示了小角距时差分时延率的优势。

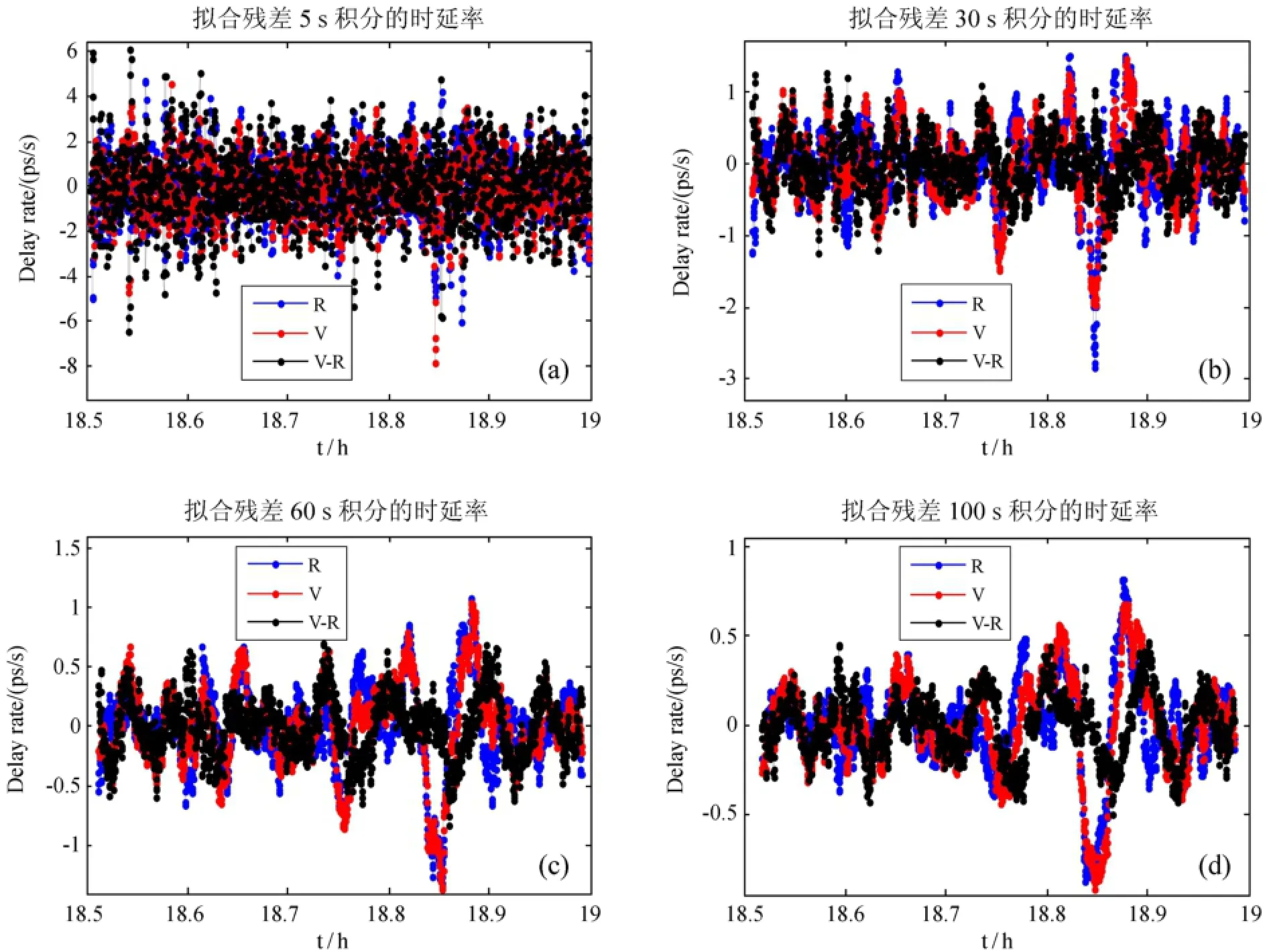
图3 大角距观测弧段，用5点直线拟合求得的Rstar和Vstar时延率残差以及差分时延率残差。拟合相位残差积分时间为(a)5 s；(b)30 s；(c)60 s；(d)100 sFig.3 Delay rates and difference delay rates in an orbital period of large seperation angles between two satellites，as derived by integrating residual correlation phases over time intervals of four values:(a)5s，(b)30s，(c)60s，and(d)100s

为了分析大角距与小角距时的差分时延率残差的主要影响因素，对5s积分的相位拟合残差进行Allan方差分析，结果如图5和图6。

由图5可知，大角距时，差分相位拟合残差的Allan方差走势与单卫星相位拟合残差的Allan方差走势有一定的相似性，说明它含有一定的中性大气与电离层的影响；同时它的走势又不同于单卫星相位的Allan方差，它偏向于热噪声的Allan方差走势，说明它也有热噪声的影响。图6中的差分相位拟合残差的Allan方差走势与热噪声的Allan方差走势十分相似，说明此时的差分相位拟合残差中基本只有热噪声的影响，而中性大气和电离层的影响基本被去除。

2 时延率和差分时延率的统计分析

利用2008年一年中日本VERA的4个台站以及国际4个台站组成的所有基线的数据，对拟合相位残差求得的时延率残差和差分时延率残差进行了统计分析，结果如表1和表2。表1与表2给出了不同积分时间、不同点数直线拟合得到的时延率残差以及差分时延率残差的RMS值，即为时延率以及差分时延率的随机误差，其中V代表Vstar，R代表Rstar，V-R代表两者的差分。

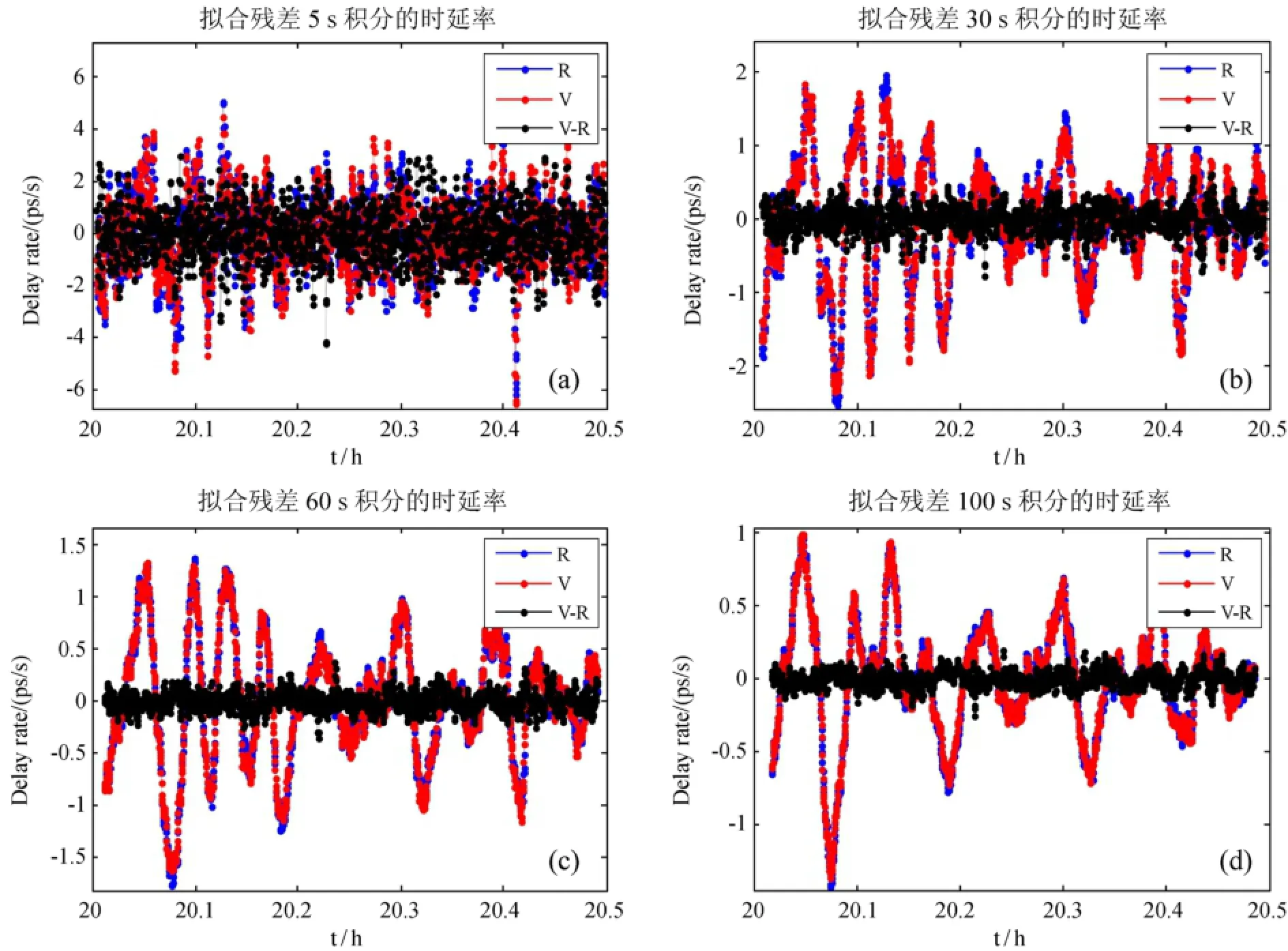
图4 小角距观测弧段，用5点直线拟合求得的Rstar和Vstar时延率残差以及差分时延率残差。拟合相位残差积分时间为(a)5 s；(b)30 s；(c)60 s；(d)100 sFig.4 Delay rates and difference delay rates in an orbital period of small seperation angles between two satellites，as derived by integrating residual correlation phases over time intervals of four values:(a)5s，(b)30s，(c)60s，and(d)100s

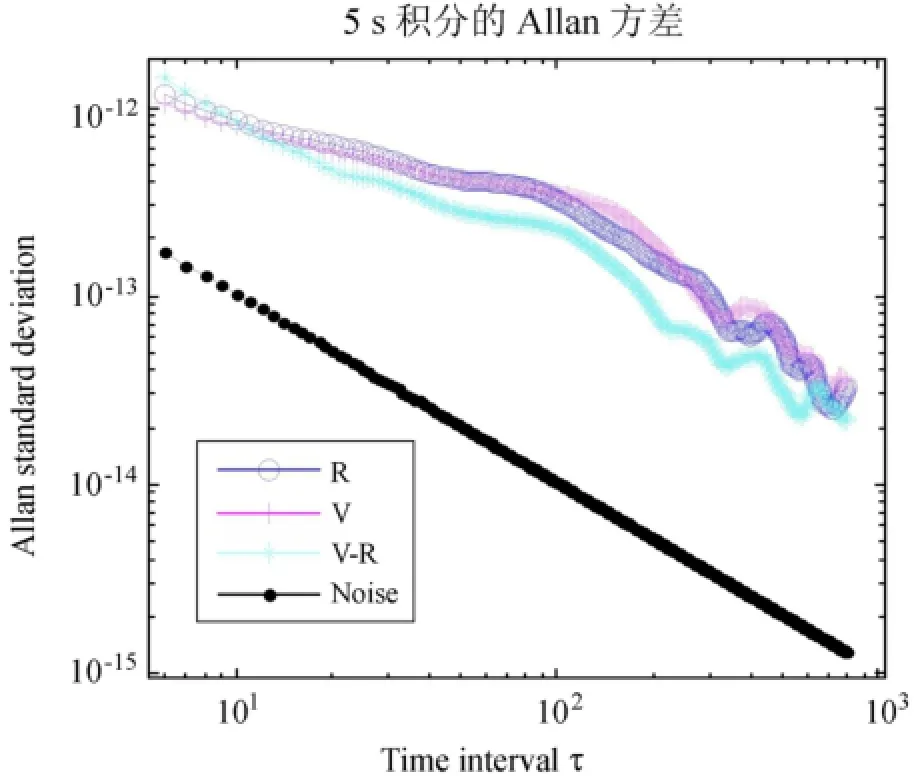
图5 大角距时的差分相位拟合残差的Allan方差Fig.5 Allan variances of correlation-phase residuals in an orbital period of large separation angles between two satellites

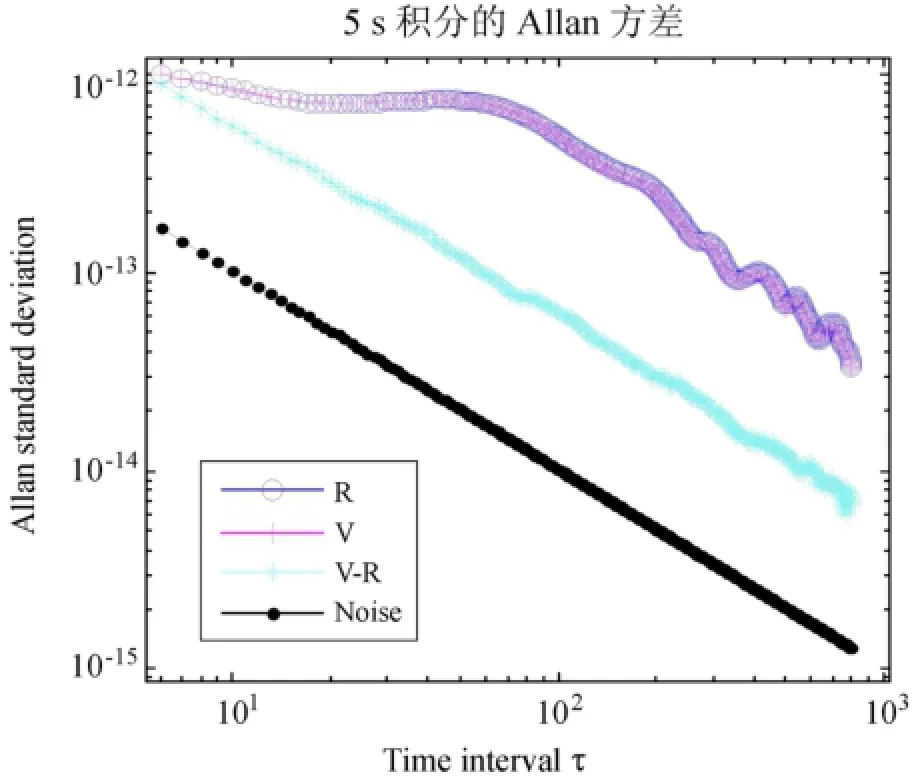
图6 小角距时的差分相位拟合残差的Allan方差Fig.6 Allan variances of correlation-phase residuals in an orbital period of small separation angles between two satellites

表1中的数据按照如下方法求得:先对Rstar与Vstar每个弧段(约30 min)的f1频点的相关相位进行9次多项式拟合后得到拟合相位残差，然后对拟合相位残差进行60 s平滑积分后分别用2、5、9点直线拟合求取时延率残差和差分时延率残差，最后将时延率残差和差分时延率残差按两卫星的角距离分组，并求它们的RMS值。表2中的数据按同样方法求得，只是将60 s平滑积分改为30 s平滑积分。

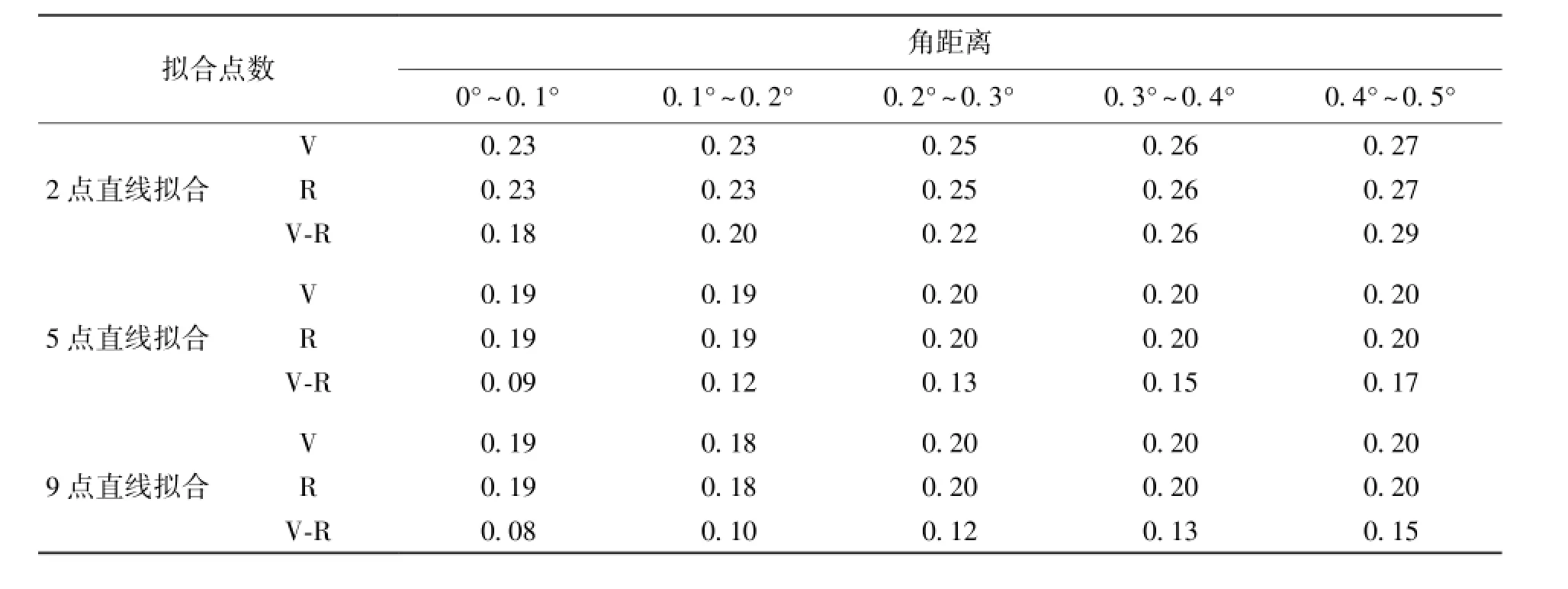
表1 60 s积分以不同点数直线拟合得到的时延率和差分时延率随机误差的统计结果(单位:ps/s)Table 1 Statistical results of random errors(in units of ps/s)of delay rates and difference delay rates derived through linear fitting to various numbers of points each with an integration time of 60s

表2 30 s积分以不同点数直线拟合得到的时延率和差分时延率随机误差的统计结果(单位:ps/s)Table 2 Statistical results of random errors(in units of ps/s)of delay rates and difference delay rates derived through linear fitting to various numbers of points each with an integration time of 30s

由表1和表2可得出下述结论:

(1)时延率和差分时延率的随机误差随拟合点数或积分时间的增加而减小。

(2)Rstar与Vstar的单卫星时延率的随机误差基本保持一致。在60 s积分2点直线拟合时，单卫星时延率随机误差随着角距离的增大而增大，这与角距离越大，天线接收信号的信噪比越低有关，说明随机误差受热噪声影响显著。在60 s积分5点和9点直线拟合时，单卫星时延率随机误差基本稳定在0.2 ps/s的水平，说明此时的热噪声影响已很小；在30 s积分2、5、9点直线拟合时，单卫星时延率随机误差都随着角距离的增大而增大，其中以2点直线拟合时最为明显，说明它们的结果都含有明显热噪声成分，意味着30 s积分并不能把热噪声限制在一个低水平。

(3)单卫星时延率的随机误差在积分30 s时是积分60 s时的1.5倍左右。

(4)差分时延率随机误差随角距离增大而增大，且差分时延率的随机误差在积分60 s时是积分30 s时的一半左右。

(5)在5点、9点直线拟合情况下，当角距离小于0.1°时，差分时延率随机误差是单卫星时延率随机误差的一半以下；当角距离大于0.1°时，差分时延率随机误差仍然小于单卫星时延率随机误差。

时延率的随机误差会因不同季度的不同降水量、不同日照时间等因素而不同，而由表1数据已得知，在60 s积分5点直线拟合时，已能把热噪声降到一个较低水平，所以把2008年的数据按不同季节，在60 s积分5点直线拟合情况下分别处理，得到了表3的结果。需说明的是，由于没有九月份的观测数据，所以秋季只包含七、八两月。

由表3可知，单卫星时延率随机误差在秋季最大、春季最小，而差分时延率随机误差在不同季节基本相当。分析原因认为，在1、2、3月份，由于天气较干燥，雨水较少，所以信号传播受中性大气的影响较小。但在7、8月份，水汽较多，使得信号传播受中性大气的影响加大，从而使单卫星时延率随机误差比春季大。但是差分时延率，不管水汽多少，总是能把相同部分去除，所以使得其随机误差在全年没有大的波动。

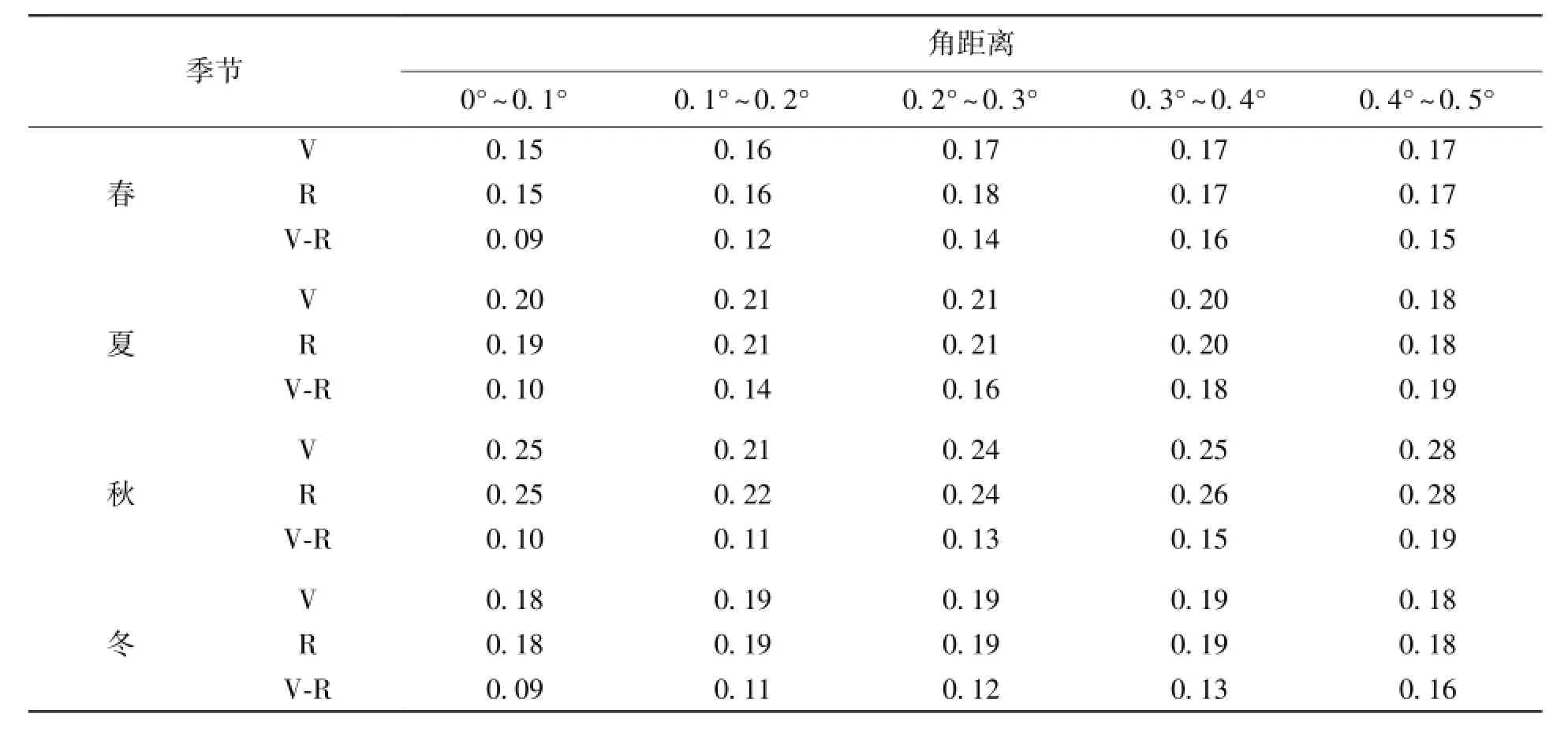
表3 60 s积分5点直线拟合得到的时延率和差分时延率随机误差在不同季节的统计结果(单位:ps/s)Table 3 Statistical results of random errors(in units of ps/s)of seasonal delay rates and difference delay rates derived through linear fitting to 5 points each with an integration time of 60s

另外，差分时延率在积分时间多长时，它的随机误差等于单卫星时延率的随机误差，也是尚未研究的课题。为此，把2008年的数据按不同季节，使用5点直线拟合分别处理，得到了表4的结果。表4显示，差分时延率随机误差等于单卫星时延率随机误差所用的积分时间，随着角距离的增大而增大，在角距离小于0.1°时，基本小于10 s，并且在秋季所用的积分时间最短。

表4 差分时延率随机误差等于单卫星时延率随机误差时所用的积分时间(单位:秒)Table 4 Integration times(in units of seconds)used when random errors of delay rates equal to those of difference delay rates

3 结 论

在角距离小于0.1°时，差分时延率的随机误差已基本不受中性大气和电离层的影响，主要由热噪声引起。在角距较大时，差分时延率的随机误差中能除去一部分中性大气和电离层的影响，其随机误差仍比单卫星时延率的随机误差要小。2008年全年的统计结果表明，在60 s积分5点直线拟合情况下，单卫星时延率的随机误差约为0.2 ps/s，且在秋季时最大。差分时延率的随机误差在0.09 ps/s～0.17 ps/s之间，在不同季节基本稳定。最后，在角距离为0°～0.1°时，差分时延率随机误差等于单卫星时延率随机误差时所用积分时间基本小于10 s。

[1] 钱志瀚.VLBI起步经历及探月工程[EB/OL].(2012-07-20)[2013-11-12].http://www.shao.ac.cn/tq/zgxy/201207/t20120726＿3621782.html.

[2] Liu Q H，Shi X，Kikuchi F，et al.High-accuracy same-beam VLBI observations using Shanghai and Urumqi telescopes[J].Science in China Series G:Physics，Mechanics and Astronomy，2009，52(12):1858－1866.

[3] Liu Q，Kikuchi F，Matsumoto K，et al.Same-beam VLBI observations of SELENE for improving lunar gravity field model[J].Radio Science，2010，45(2):1－16.

[4] Iwata T，Takahashi M，Namiki N，et al.Mission instruments for lunar gravity field measurements using SELENE sub-satellites[J].Journal of the Geodetic Society of Japan，2001，47(1):558－563.

[5] Liu Q H，Chen M，Goossens S，et al.Applications of same-beam VLBI in the orbit determination of multi-spacecrafts in a lunar sample-return mission[J].Science China Physics，Mechanics and Astronomy，2010，53(6):1153－1161.

[6] Hanada H，Iwata T，Kikuchi F，et al.Differential VLBI observations of two sub-satellites of SELENE(KAGUYA)，OKINA and OUNA for lunar gravimetry[J].Journal of the Geodetic Society of Japan，2009，55(2):203－221.

A Study of Difference Delay Rates Derived from Processing of Same-Beam VLBI Data

He Qingbao1，2，Liu Qinghui1，Zheng Xin1，2，Wu Yajun1，2，Tang Mingle1，2
(1.ShanghaiAstronomical Observatory，Chinese Academy of Sciences，Shanghai 200030，China，Email:qbhe＠shao.ac.cn；2.University of Chinese Academy of Sciences，Beijing 100049，China)

As shown by our analyses difference delay rates from SELENE same-beam VLBI data are almost not influenced by long-term effects on radio signals from the ionosphere and neutral atmosphere.The short-term effects on radio signals from the atmosphere can be mostly eliminated if the separation angle between two satellites is small(＜0.1°)，but becomes more appreciable and more difficult to be eliminated as the separation angle increases.We further integrate the residuals of correlation phases for a set of data after fits to their systematic trends are subtracted.The data were observed with all baselines of 8 VLBI stations through 2008.Some integrations are over time intervals of 60s or 30s，and each integration generates a data point for detailed analyses.We apply linear fits to every 5 data points to find delay rates and difference delay rates. Statistics of these show that rms values of random errors of delay rates of two satellites are about 0.20ps/s and 0.32ps/s，respectively.Our statistics also show that rms values of random errors of difference delay rates of two satellites are 0.09ps/s to 0.17ps/s and 0.19ps/s to 0.32ps/s，respectively.Random errors of delay rates are statistically small in the spring and larger in the autumn，but those of difference delay rates are stable throughout the year.

VLBI；Delay rate；Difference delay rate；Same-beam

V557＋.5

A

1672－7673(2014)03－0247－08

2013－10－23；

2013－11－08

贺庆宝，男，硕士研究生.研究方向:同波束VLBI时延解算.Email:qbhe＠shao.ac.cn