金属固体材料杨氏模量的静态拉伸法测量改进

(湖南科技学院 电子工程系,湖南 永州 425199)

杨氏模量是表征材料性质的一个重要的物理量，是工程技术设计中常用的参数，通常只与材料的性质、温度及其加工制造的方法有关，而与外力及物体的几何形状无关，对它的准确测量具有很重要的工程实践意义。测量材料杨氏模量的方法有很多，如拉伸法、压入法[1]、弯曲法[2][3]和游标法[4]等等。拉伸法是最常用的方法之一，这是因为金属丝的伸长量非常小，一般的实验仪器及实验方法很难精确测量，故通常都是采用光学放大法(即光杠杆放大法)实现微小伸长量的测量。但实验室现有的实验仪器在调节、测量读数等方面均存在一些不便，本文对实验室现有实验仪器和测试方法进行改进，从而简化实验操作、减小误差，能有利于提高杨氏模量的测量精度。

1 测量原理

1.1 胡克定律和杨氏弹性模量

当固体受外力作用时，它的体积和形状将要发生改变，这种改变，称之为形变。物体的形变一般可分为弹性形变和塑性形变。当外力不太大时，物体的形变与外力成正比，且外力停止作用物体立即恢复原来的形状和体积，这种形变称弹性形变。当外力较大时，物体的形变与外力不成比例，且当外力停止作用后，物体形变不能完全消失，这种形变称为范性形变。范性形变的产生，是由于物体形变而产生的内应力(大小等于单位面积上的作用力)超过了物体的弹性限度(屈服极限)的缘故。如果再继续增大外力，当物体内产生的内应力超过物体的强度极限时，物体便被破坏了。胡克定律指出：在物体的弹性限度内，胁强与胁变成正比，其比例系数称为杨氏模量(记为E)。

在数值上等于产生单位胁变时的胁强。它的单位与胁强的单位相同。

设有一根长为L，横截面积为S的金属固体材料(如：钢丝)，在外力F作用下伸长了，则：

(1)

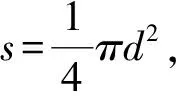
(2)

式(2)表明，对于长度为L、直径为d和所加外力为F相同的情况下，杨氏模量E大的金属丝而其伸长量却比较小。因而，杨氏模量是表征材料性质的一个重要的物理量，是工程技术设计中常需涉及的重要参数之一，通常只与材料的性质和温度有关，而与外力及物体的几何形状无关。对一定材料而言，E通常可以看作是一个常数，它只与材料的构造、化学成分等方面有关。杨氏模量的大小标志了材料的刚性。

为能测出金属丝的杨氏模量E，必须准确测出上式中右边各量。其中L、d、F都可用一般方法测得，唯有△L是一个微小的变化量，用一般量具难以测准，为了测准细小钢丝的微小长度变化，实验中采用了光杠杆放大法进行测量。因为光杠杆放大法具有稳定性高、易操作、受环境的干扰小等特点，所以在许多科研生产和生活等领域都得到广泛应用。

1.2 光杠杆和镜尺系统是测量微小长度变化的装置[3]

光杠杆基本组成如图1(a)所示，它实际上就是一块附有三个足尖的平面镜。三个足尖的边线可连成一等腰三角形。前两足尖刀口与平面镜应在同一平面内(平面镜俯仰角可以调节)，后足尖在前两足尖刀口的中垂线上。镜尺系统实际上就是一把竖立的毫米刻度尺和在尺子旁的一台望远镜组成。光杠杆与镜尺系统组成如图1(b) 所示的测量系统。

图1 (a) 光杠杆 图1 (b) 杨氏模量测量系统

将光杠杆和镜尺系统按图1(b) 安装好，并按仪器调节步骤调节好全部装置之后，就会在望远镜中看到由镜面M反射的直尺(标尺)的像。标尺是一般的米尺，但中间刻度为0。其光路部分如图2。图中M1表示钢丝处于伸直情况下，光杠杆小镜的位置。从望远镜的目镜中可以看见水平叉丝对准标尺的某一刻度线n0，当在钩码上增加砝码(第i块)时，因钢丝伸长致使置于钢丝下端附着在平台上的光杠杆后足P跟随下降到P′，PP′即为钢丝的伸长△Li，于是平面镜的法线方向转过一角度θ，此时平面镜处于位置M2。在固定不动的望远镜中会看到水平叉丝对准标尺上的另一刻线ni，ni-n0就是放大后的钢丝伸长量△ni(即△ni=ni-n0)，常称作视伸长。假设开始时对光杠杆的入射和反射光线相重合，当平面镜转一角度θ，则入射到光杠杆镜面的光线方向就要偏转2θ，故∠n0Oni=2θ，因θ甚小，OO′也很小，故可认为平面镜到标尺的距离D≈On0，并有：

(3)

(4)

式中b为后足至前足连线的垂直距离，称为光杠杆常数。从以上两式得：

(5)

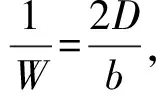
(6)

常用单位是：N/m2或Pa。式中d为钢丝的直径。

图2 光杠杆放大原理图

2 实验改进

2.1 测量钢丝长度L的改进[5]

在测量钢丝长度L时，由于钢丝上下端装有紧固夹头，同时钢丝处于竖直拉长状态，这给测量带来很大不便。一来由于紧固夹头的阻碍，很难将钢卷尺贴近钢丝，而必须将钢卷尺放置在距离钢丝有一定距离的位置进行测量，这样由于人眼读数的视差，必然会减低读数准确度；二来由于钢丝处于竖直拉长状态，测量者要将钢卷尺竖直拉长后再去读数，这样就很难保证视线与刻度对齐，从而产生视差，降低读数精度。针对这个问题，可以考虑将钢卷尺和固定钢丝的装置的一端固连在一起，并使得钢卷尺尽量靠近细钢丝。需要读数的时候，将钢卷尺拉出，由于钢卷尺的一端固定，这将大大降低了单人操作时的难度，可以提高测量精度。

2.2 测量镜尺间距D的改进

在测量镜尺间距D时，由于距离较远，很难保证钢卷尺水平放置、不弯曲而且两端对齐，显然这样带来的误差将会相当大。为了减少该误差，可以参考光学实验中测量光学元件间距时采用带刻度的光具座的方法，将望远镜、钢丝固定装置置于一个带有刻度的导轨上，从而简化测量和提高精度。

2.3 测量光杠杆前后足间距b的改进[6]

在测量光杠杆前后足间距b时，不能保证完全是垂直距离，同时由于光杠杆的尺寸和形状问题，也会使得游标卡尺不能很好地卡紧前后足。可以考虑将光杠杆置于白纸上，用铅笔描出光杠杆三足位置，然后连接两个后足，再过前足作后足的垂线，测量前足到垂足的距离，则可以比较简便地测出前后足间距。但是这样操作则不能用游标卡尺测量前后足间距，故而将会损失一定测量精度。

2.4 测量视伸长△ni的改进

由于采用了光杠杆多次成像的方法放大了微小位移，故而对原来位移的微小扰动，也会同时放大成相当大的干扰，从而影响读取视伸长数值的精确度。在实验中发现，望远镜中的标尺像总是在晃动，很难保证叉丝保持对齐某个刻度线，严重的时候叉丝对准的刻度甚至会有一个相当大的变动范围，大大超过仪器本身的测量误差限度。考虑到视伸长△ni对本实验精确度的影响极大，应该着重改善这个问题。

首先应该尽可能地减少钢丝受到的扰动。实验时应该尽量小心，保持桌面的平稳，并且尽量在标尺像晃动不太剧烈的时候迅速读数。

其次应该通过多次读取数值来消减误差。在加砝码和减砝码后，应该在标尺晃动不太剧烈时，读取几组数据，然后再求平均，通过平均的作用消减读取位置偏离真实位置的误差。

再次应该在条件允许下改善实验设备。由于标尺像在不断晃动，要在它晃动的时候看清对齐的刻度并估读数字是很困难的，所以如果条件允许，可以将望远镜改进为带有摄像功能的摄像望远镜。在标尺像晃动不太剧烈时，拍摄几组照片，之后再读取静止的照片中的读数，此时就能获得更好的精确度。

3 数据记录与处理

3.1 计算钢丝弹性模量

按着改进后的实验装置和方法进行实验，记录数据如下：

钢丝长度L=39.60cm，平面镜到标尺的距离D=102.20cm，光杠杆前后足间距b=8.500cm

表1 钢丝直径d测量结果(螺旋测微器零点误差x0=-0.320mm)

表2 加砝码后标尺的读数n

表3 用逐差法求标尺读数改变量△n

3.2 计算钢丝弹性模量的不确定度

L、D、b只测量一次，只有B类不确定度，估计其误差限为△L=0.3cm，△D=0.5cm，△b=0.02cm，故：

d的不确定度：

△n的不确定度：

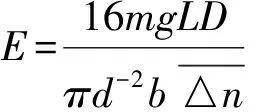
∴ lnE=lnL+lnD-2lnd-lnb-ln △n+ln 16+lnm+lng-lnπ

两边同时求微分，得到：

将上式中d改为u，并取平方和的根：

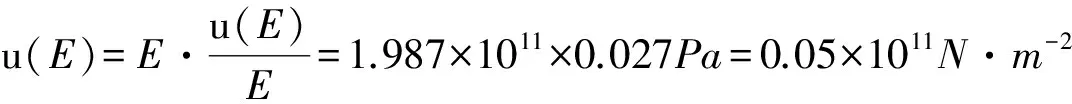
最终结果为：E±u(E)=(1.99±0.05)×1011N·m-2

4 分析与结论

通过查阅相关资料可得，钢丝的弹性模量理论值约为1.92×1011～2.16×1011N·m-2[7]，不妨取E真=2.04×1011N·m-2作为真值的估计值，并以此计算绝对误差与相对误差：

△N=E-E真=(1.99-2.04)×1011N·m-2=-0.05×1011N·m-2

可以看出，实验的误差是比较小的。

下面估算各测量值不确定度对最终结果的不确定度的贡献为：

表4 各测量值的相对不确定度分量

可见，u(△n)和u(d)的影响均很大，其贡献主要来自uA(△n)/△n、uB(△n)/△n和2uB(d)/d。实际上只考虑这三项的方差合成就可达2.6%，与u(E)/E=2.7%相差很小。表4所述不确定度分量主要来自仪器误差，一般只能通过仪器校正来减小，因此很难再通过改善测量方法来提高其准确度。反之也说明了本次实验在测量方法的选择上是恰当的。△n、d的测量中采取了多次重复测量的方式，实验中对d的测量没有给E带入很大的误差，但△n的测量则带入了很大的误差，故而在对△n的测量可能存在较大问题。下面对△n带来的误差可能性进行分析：

i/测量次数12345△ni/标尺读数改变量(CM)1．8951．9401．9401．8301．745

图3 △n1(标尺读数改变量)的散点图

散点图显示，第五个数据波动相当大，很可能是由于测量有误而读出的坏数。由于测量次数只有五次，故而不能用拉依达法则判断其是否坏数，而应该用检验准则来判断。

=0.05202163

先将△n5剔除，计算剩余数据的平均值和单次测量标准偏差：

根据测量次数n=5，查表得到若选置信概率为0.99和0.95时的对应K值为：

K(5,0.99)=6.53，K(5,0.95)=3.56，分别设为X、Y，则有：

∵X·S=6.53×0.05202163=0.33970,Y·S=3.56×0.05202163=0.18520

∴Z

故而△n5并不是坏数，只是多次测量中的一次比较极端的情况，应该保留。重新考虑△n的测量带来的随机误差，发现测量次数仅有5次，故而多次测量中的极端情况△n5带来的随机误差使得测量结果的A类不确定分量特别大。为了消减误差，在测量△n的时候，应当进行次数更多的测量，获取更为平均的结果。但应该注意，测量次数不宜过多，否则可能会带来新的测量误差和粗大误差。

由以上分析可得，对实验装置和方法改进后的测量结果稳定可靠，与理论值吻合较好，测量精度有较大提高，误差控制在2.45%左右，基本能满足对钢丝杨氏模量的测量要求。

参考文献：

[1] 侯君达,潘澍.压入法测定金属材料的杨氏模量[J].理化检验, 1999,(9):396-398.

[2] 梁霄, 田源等.横梁弯曲衍射法测杨氏模量实验仪的研制[J].物理实验,2011,(8):31-33.

[3] 李文斌,刘旺东.大学物理实验[M].湘潭:湘潭大学出版社,2009:56-65.

[4] J H Avery, A W Klngram.MondernLaboratoryPhysics[M].London: Heinmann Educational Books Ltd,1976.55-57.

[5] 陈薇薇,刘艳凤.拉伸法测量金属丝杨氏模量的实验改进[J].牡丹江师范学院学报,2007,(1):13-14.

[6] 庄建,青莉.关于实验“拉伸法测杨氏模量”的思考[J].实验科学与技术,2006,(3):69-71.

[7] 万志龙.利用螺旋测微器测量金属丝的杨氏模量[J].德州学院学报,2007,(6):22-24.