等离子体参数对中性束注入下快离子自举电流影响

黄千红，龚学余，曹锦佳，杨 磊

（南华大学 核科学技术学院，衡阳421001）

托卡马克要稳态运行在高性能状态，等离 子体电流绝大部分应由自举电流产生。在通常情况下等离子体自举电流是由背景等离子体压强分布的各向异性产生［1－8］，除此之外，在聚变装置中通过聚变反应或由辅助加热和电流驱动等产生的高能量粒子也将引起等离子体压强的各向异性，进而产生附加的自举电流，因此对这部分高能量粒子产生的自举电流进行进一步研究，对完善自举电流研究及等离子体电流的产生和控制研究，具有极其重要的意义。

中性束加热和电流驱动被广泛应用于聚变装置中。在高能量中性粒子注入等离子体过程中，中性粒子与背景等离子体通过电荷交换和离子化过程产生离化并与背景等离子体交换能量产生快离子，中性粒子注入后产生的快离子也会产生压强分布的各向异性，从而产生自举电流。不少人研究了由于核反应产生的α粒子自举电流，计算表明其产生的自举电流不到背景等离子体产生的自举电流的10%［9，10］，且由于处理α粒子产生的自举电流仅限于各向同性源，不能应用于由中性束注入和射频波加热产生的高能离子产生的自举电流情形。Taguchi［11］研究了环截面大纵横比情况下由中性束注入产生的高能离子产生的自举电流，给出了理论表达式和输运系数的数值计算，并没有计算给出自举电流的大小和分布。在文献［12］中，数值计算了中性束注入加热下产生的快离子自举电流密度的分布并讨论了由快离子平行动量输运引起的电子回流效应的影响，分析了中性束参数对净电流密度分布和大小的影响。本文进一步研究了大纵横比托卡马克中背景等离子体参数对中性束注入产生的快离子自举电流净电流密度的影响。

1 物理模型

考虑轴对称磁场中等离子体，磁场B＝I（ψ）Δφ＋ Δφ× Δψ，φ 是环向角，2πψ 是极向通量。高能中性束粒子注入等离子体中通过与背景等离子体电荷交换和离子化形成快离子，快离子与背景等离子体通过库伦碰撞而逐渐慢化，在速度空间形成一定的分布所产生的附加压强的各向异性引起快离子自举电流的产生。忽略空间轨道损失，考虑稳定状态中性束注入产生的快离子回旋平均分布函数由漂移动力学方程决定［8］：

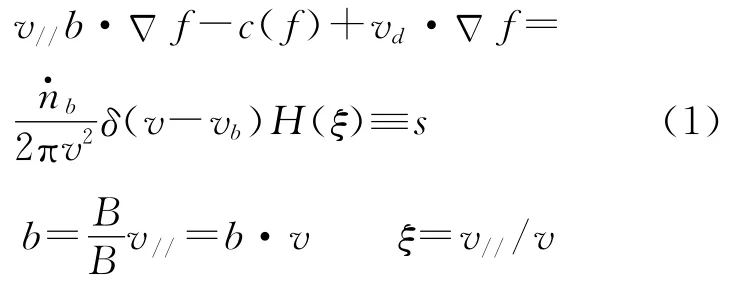
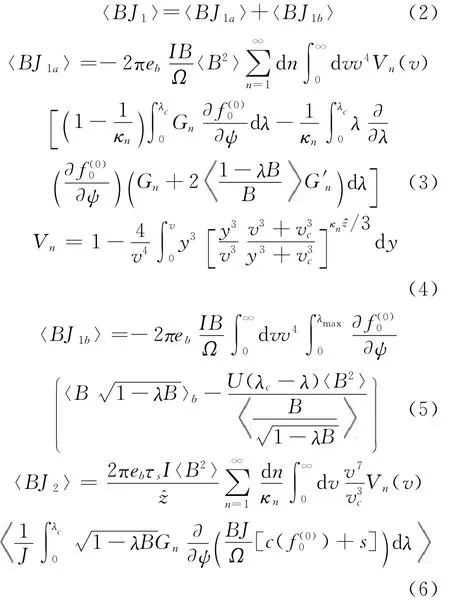
在忽略回旋角散射情况下快离子自举电流主要由J1b决定［11］，式（3）～式（6）可以用来计算由于中性束注入或射频波加热等离子体产生的快离子自举电流。

在大纵横比托卡马克中环磁面情况下，环向磁场：B＝B0／（1＋εcos（θ）），其中ε＝r／R0，R0是环大半径，r、θ分别是小半径和极向角。在均匀磁场极限条件下，特征函数Gn（λ）（n＝1，2…）和（m＝0，1，2…）为勒让德多项式和它们的特征值为κn＝2n（2n－1）和κm＝2m（2m＋1）。可得到。

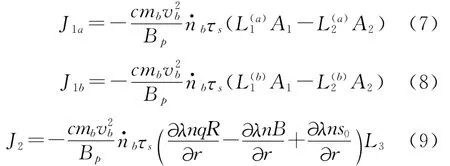
式中：Bp是极向磁场，A1，A2是径向梯度驱动力，输运系数和回旋角散射函数H（ξ）具体形式参考文献［11］。总自举电流可表示为［16］：

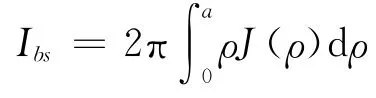
快离子产生率［17］。

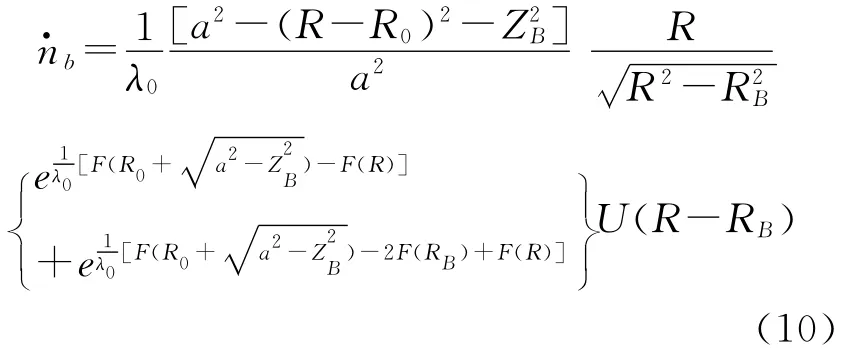
其中：

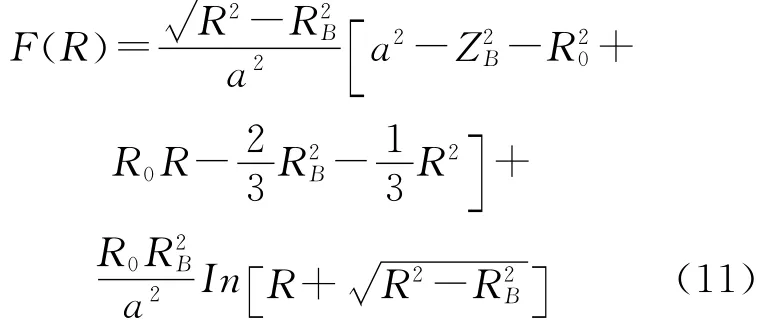
式中，λ0是最大质子密度处的中性束粒子的吸收平均自由程，ZB是中性束注入点在中心轴Z方向坐标，RB是注入点到中心轴距离。

考虑由于快离子平行动量的输运，束自举电流伴随有电子的回流效应，净电流密度为：，F表示快离子自举电流屏蔽因子［18］：

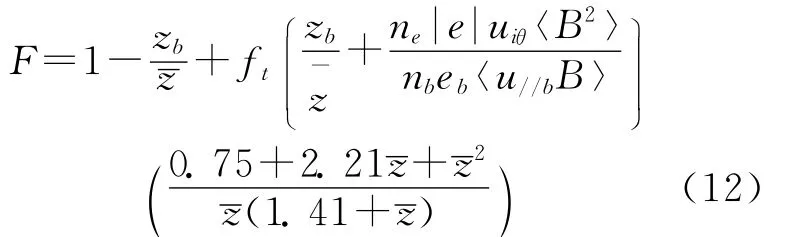
z是有效电荷数，zb是快离子电荷数。根据平行方向离子动量平衡，方程（12）中正比于uiθ的项约为0（me／mi）⅟2［18］，可以忽略，进而可以得到：

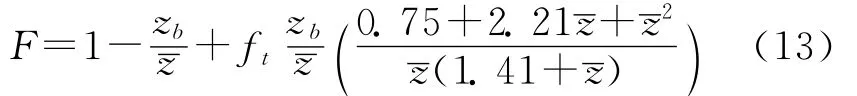
2 计算结果和讨论

计算中采用的托卡马克等离子体和中性束参数为 HL－2A参数：大半径：R0＝1.64m；小半径：a＝0.45m；环向中心磁场：Bt＝2.8 T；环向等离子体电流：Ip＝450KA，中性束采用垂直注入，相关参数：能量E＝25keV，等效流强IB＝2.3A。为简化计算，设中性束从中平面注入，即ZB＝0，并取中性束为氢中性束。

密度和温度分布如下：

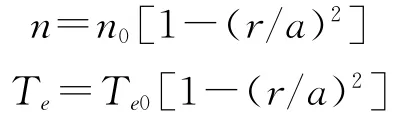
图1给出了中性束垂直注入时净电流密度随等离子体电子温度变化曲线，中心温度分别取Te0＝0.8、0.7和0.6keV，中心密度取n0＝5.0×1020m－3。从图中可以看到，净电流密度随等离子体电子中心温度的增大而增大，与背景等离子体自举电流和聚变产生的α粒子自举电流变化是相同的［4，5，19］。

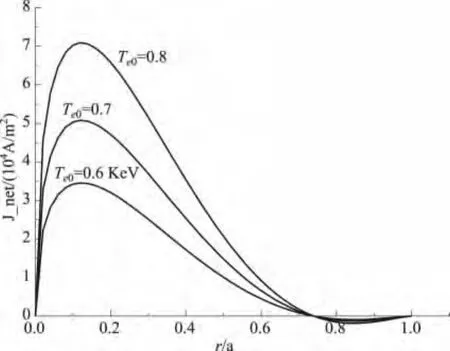
图1 净电流密度随等离子体温度变化，Te0＝0.8，0.7，0.6KeV，n0＝5.0×1020 m－3Fig.1 The profile of net current density changes for different plasma temperature，Te0＝0.8，0.7，0.6keV，n0＝5.0×1020 m－3

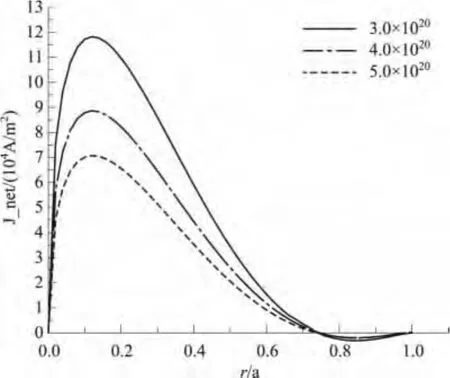
图2 净电流密度随等离子体密度变化，n0＝3.0，4.0，5.0×1020 m－3，Te0＝0.8keVFig.2 The profile of net current density changes for different plasma density，n0＝3.0，4.0，5.0×1020 m－3，Te0＝0.8keV

图2给出了中性束垂直注入时净电流密度随等离子体密度的变化情况，图中三条曲线分别对应于n0＝3.0，4.0，5.0×1020m－3，这里的电子温度均为Te0＝0.8KeV。由图可知，净电流密度随等离子体密度的增大而减小，这主要是因为随着背景等离子体密度的增大，束与背景等离子体碰撞作用的有效截面增大，束的透入减少。

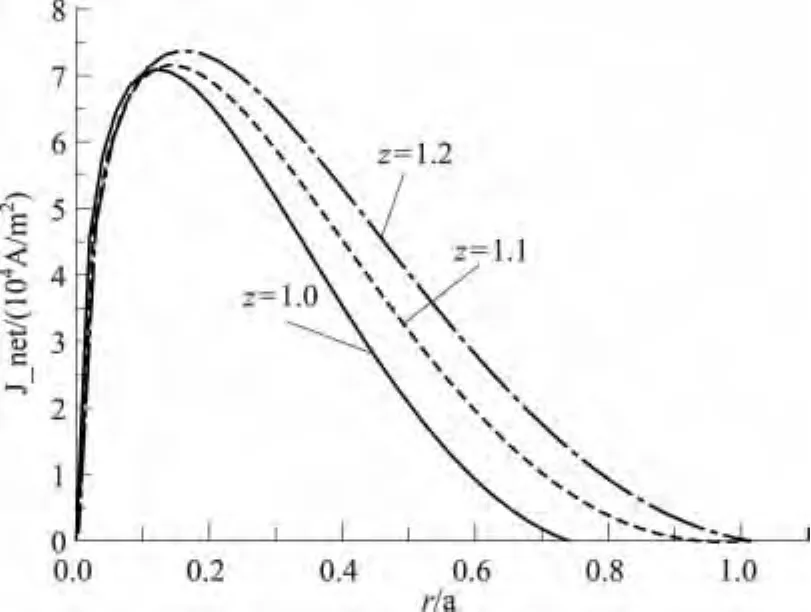
图3 净电流分布随有效电荷数变化，Z＝1.0，1.1，1.2，Te0＝0.8keV，ne0＝5.0×1020 m－3Fig.3 The profile of the net current density changes for different effective charge numbers，Z＝1.0，1.1，1.2，Te0＝0.8keV，ne0＝5.0×1020 m－3

图3给出快离子净电流密度随有效电荷变化曲线，有效电荷分别对应于Z＝1.0，1.1，1.2，密度和温度均取为ne0＝5.0×1020m－3，Te0＝0.8keV。由图可知，有效电荷对净电流大小影响不大，但随有效电荷增大，净电流密度峰值向等离子体边缘偏移。

3 结论

本文在文献［12］的基础上进一步研究了由于中性束注入轴对称磁场托卡马克装置产生的快离子自举电流净电流密度的分布随背景等离子体参数变化的关系。计算结果表明：快离子净电流的大小随背景等离子体温度的升高而增大，随等离子体密度的增大而减小，等离子体有效电荷对净电流密度大小影响较小，但随有效电荷的增大快离子净电流密度的峰值向等离子体边缘偏移。

［1］ Bickerton R J，Connor J W and Taylor J B，Diffusion Driven Plasma Currents and Bootstrap Tokamak，Nature Phys.Sci.1971，229（25），110.

［2］ Zarnstorff M C，Bell M G，Bitter M，Bootstrap current in TFTR，Phys.RevLett.60，1988，1306.

［3］ Hirshman S P and Jardin S C，Two－dimensional transport of Tokamak plasmas，Phys.Fluids，1979，22，731.

［4］ Kessel C E，Bootstrap current in a tokamak，Nucl.Fusion，1994，34，1221.

［5］ 龚学余，谢安平，彭晓炜，等.Tokamak等离子体不同运行模式下产生的自举电流，南华大学学报（自然科学版），2005，19（1）：1.

［6］ Wang Zhong－tian and Wang Long，Bootstrap current in spherical tokamaks，Plasma Sci.Technol，2003，5（3），1767.

［7］ Andrade M C R and Ludwig G O，First estimate of bootstrap current in the ETE small aspect ratio tokamak，Plasma Phys.Control.Fusion，1997，39，1041.

［8］ Kikuchi M，Azumi M，Tsuji S，et al，Bootstrap current during perpendicular neutral injection in JT－60，Nucl.Fusion，1990，30（2），343.

［9］ Hsu C T，Shaing K C，Gormley R P and Sigmar D J，Bootstrap current induced by fusion born alpha particles，Phys.Fluids，B4，1992，4023.

［10］ Kolesnichenko Ya I，The role of alpha particles in tokamak reactors，Nucl.Fusion，1980，20（6），727.

［11］ Taguchi M，Bootstrap current in NBI heated plasmas，Nucl.Fusion，1996，36，657.

［12］ Qian－hong Huang，Xue－yu Gong，Jun Yu，et al，Bootstrap current of fast ions in neutral beam injection heating，Phys.Scr.85，2012，055503.

［13］ Cordey J G，Effects of particle trapping on the slowingdown of fast ions in a toroidal plasma，Nucl.Fusion，1976，16（3），499.

［14］ Taguchi M，Approximate expression for beam driven current in tokamak plasmas，Nucl.Fusion，1992，32（1），143.

［15］ Hsu C T，Catto P J and Sigmar D J，Neoclassical transport of isotropic fast ions，Phys.Fluids B2（2），1990，280.

［16］ Shi Bing－Ren，Analytic description of tokamak equilibrium sustained by high fraction bootstrap current，Chinese Phys.2003，12，626.

［17］ Rome J A，Callen J D and Clarke J F，Neutral－beam injection into a tokamak：PartⅠ：Fast－ion spatial distribution for tangential injection，Nucl.Fusion，1974，14，141.

［18］ Hirshman S P and Sigmar D J，Neoclassical transport of impurities in tokamak plasmas，Nucl.Fusion，1981，21，1079.

［19］ 黄千红，谢安平，刘柏青，等.聚变反应中产生的α粒子的自举电流，南华大学学报（自然科学版），2008，22（2）：19.