黑名单快速匹配算法的研究
戴琳琳,张晨阳,苗 凡,阎志远
(中国铁道科学研究院 电子计算技术研究所,北京 100081)
随着互联网技术的深入发展,中国铁路客票系统也实现了互联网在线售票,目前中国铁路互联网注册用户达7 000多万,每天用户的平均登录数达数百万,高峰时可达千万。在互联网售票中,恶意购票者或被政府管理机构定义为恶意用户,将被列入黑名单。如何实现在百万级乃至千万级的黑名单中,快速定位给定的用户信息成为影响用户体验至关重要的环节。黑名单(Blacklist)指记录恶意用户的信息列表,用户信息可以是电话号码、身份证号、IP地址或用户名等,本文以电话号码黑名单的快速匹配为例,阐述其相应的实现算法。
1 问题引入
问题假设给定了电话号码黑名单集合,需要判定一个给定号码是否落在黑名单中。
黑名单的输入有以下3种形式:
(1)给定1个完整号码,如13500001234。
(2)给定1个号码前缀,如1381010XXXX。
(3)给定1个号码区间,如[15901015555,15901023333]。
每秒钟可能有几十万次的匹配请求。每次请求的输入是一个完整的电话号码,系统输出‘是’或‘否’,表示该号码是否在黑名单中。
2 二分查找定位算法
2.1 黑名单描述
如何在系统里存储和表示黑名单,是解决黑名单问题的关键之一。一个最简单的想法是用位图来描述所有可能的电话号码。假定最大的电话号码是19999999999,那么它需要内存、空间开销很大。不同国家的电话号码长度不一样,采用位图的算法很难保持通用性。
更形象的做法是把黑名单表示为数轴上一些区间的集合。对于数轴上给定的一个点,问题转化一个穿刺查询(Stabbing Query);若该点落在任意一个区间里,则返回‘是’,否则返回‘否’。
很明显,第2种描述方式将会使用更少的空间。对于黑名单输入的3种方式都能很容易地换化为区间,为保持通用性,使用64位整数表示电话号码。使用C++描述黑名单区间数据结构如下:


2.2 区间扁平化
在开始查询前对区间数据进行预处理能够有效提高查询效率。下面的算法能将原始输入中所有相交的或者相邻的区间合并,并按照顺序排列。这里使用到的算法是采用特化的模板less用于对黑名单区间集合进行排序,排序的标准是黑名单区间的左端点的比较,那么相交或相邻的区间就会依序排序到一起,方便合并,使用C++描述黑名单区间扁平化算法如下:


例如:
输入区间:[100, 500] [300, 600] [100, 150][601, 601] [700, 900]
输出区间:[100, 601] [700, 900]
2.3 算法实现
算法基本思路是:需要查找的黑名单已经处理为既不相交、也不相邻、并按顺序排列的区间集合,用二分查找可以较快定位待查询的号码。使用C++描述二分查找定位算法如下,其中,disjoint为黑名单区间集合,q为待查询的号码数值。

算法优点:实现简单。目前C++标准std库的组件都支持二分查找法,实现更为方便。
算法缺点:
(1)比较次数为O(logN),其中N为区间的数目。
(2)无法有效支持黑名单的动态增加或删除,如果需要增加新的黑名单,需要重新生成黑名单。
(3)若给出的待查号码为字符串,没有考虑将串转化为UINT64的开销。
3 字典树算法
3.1 黑名单描述
算法基本思路是:将黑名单转化为前缀集合,使用字典树(Trie)进行最长前缀匹配(Longest Prefix Match)。
构造5位数字电话号码前缀字典树的例子如图1所示,包括95588,9526X,766XX。其中X表示任意一个数字。
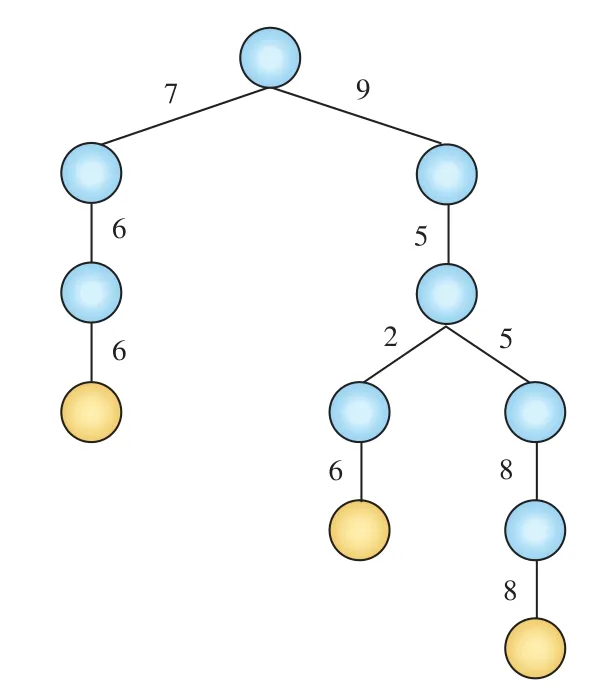
图1 构造5位数字电话号码前缀字典树示例
从图1可以看出,对于号码前缀的公共部分,其存储空间是共享的。匹配时,从根节点出发,沿着边的指示前进,如果遇到叶子节点(橘色),说明匹配成功,号码属于黑名单;否则匹配失败。
3.2 构建前缀集合
对于黑名单输入中给定完整号码和前缀的情况很容易构建前缀集合,但如果给定号码区间,需要用下面的算法将其转化为一系列前缀。

例如输入[95588, 96600],输出结果如下:

[95589, 95589] Prefix = 95589
[95590, 95599] Prefix = 9559
[95600, 95699] Prefix = 956
[95700, 95799] Prefix = 957
[95800, 95899] Prefix = 958
[95900, 95999] Prefix = 959
[96000, 96099] Prefix = 960
[96100, 96199] Prefix = 961
[96200, 96299] Prefix = 962
[96300, 96399] Prefix = 963
[96400, 96499] Prefix = 964
[96500, 96599] Prefix = 965
[96600, 96600] Prefix = 96600
3.3 算法实现
传统字典树的实现主要考虑以下2种情况:
(1)对于树节点的分支比较少的情况,可以在每个节点中分配固定数目的分支指针。这样做的好处是查询快速,但是空间浪费大。
(2)对于节点的分支比较多的情况,可以将分支组织成链表甚至散列表,目的是节省空间,但是查询分支效率受到影响。
在电话号码黑名单匹配的这种应用中,其分支数目为10,以上2种实现方式都有很大缺点。
采用三叉树(TST,Ternary Search Tree)可以比较好地解决这个问题。三叉树结合了查找二叉树(BST)和字典树(trie)的优点,能够实现前缀匹配操作,并保持较小的空间消耗。在效率方面,可以理解为TST在节点中寻找下一路径指针时进行了一次二分查找。平均而言,由于实际的分支因子(Branching Factor)远小于10,因此查询的效率仍然很高。
三叉树与传统的二叉树相比,区别是三叉树有3个字节点,分别是左节点(left),中间节点(mid),右节点(right)。插入关键字(key) 的时候,从树根作为当前节点开始(树为空的时候树根为nil),一个字符一个字符的递归执行下面过程:
(1)如果当前节点为 nil,则创建一个新的节点,将当前字符保存在节点中,将其设置为当前节点。
(2)如果当前字符和当前节点保存的字符都为‘/0’,将数据存于当前节点,终止调用。
(3)如果当前字符小于当前节点保存的字符,那么递归将当前字符插入节点的左子节点,大于则插入右子节点;相等则将下一个字符插入当前节点的中间子节点。
搜索的过程和插入类似,把关键字一个字符一个字符的和树中节点保存的字符进行比较,同样从树根开始递归执行。
(1)如果当前节点为 nil,则查找失败。
(2)如果当前字符比节点中的小,递归对左子节点查找,依然比较当前字符。
(3)如果当前字符比节点中的大,递归对右子节点查找,依然比较当前字符。
(4)如果当前字符与节点中的相等且都为‘/0’,则这个节点中就存着关键字对应的值,终止调用。如果相等但是不是‘/0’,则递归对中间子节点查找,比较字符为下一个字符。
存储 ‘42’,‘766’,‘767’,‘9526’,‘95588’串的TST树如图2所示。

图2 TST树示例图
类似于其他字典树数据结构,三叉树里每个节点代表存储串的一个前缀,所有存储在一个节点的中间树的串都以该节点的字符为前缀。
类似于二叉树,三叉树依赖于存储串的插入次序,可以是平衡的或非平衡的。在一个存储n个串的平衡三叉树中查找一个m长度的串,需要O(m+log n)次字符的比较。同时,TST也可以使用节点压缩方法来减少节点数,比如节点‘4-2’,‘7-6’,‘9-5’,‘5-8-8’,在压缩的三叉树中,每当插入一个新节点,最多一个现有的节点需要分裂。
算法优点:
(1)时间复杂度O(m+log n),节点访问次数不会超过电话号码的长度。
(2)对于匹配失败的情况(号码不在黑名单中),数字比较次数往往远小于号码长度。
(3)能够有效支持黑名单的动态增加和删除。
(4)若给出的待查号码为字符串,无须将其显式转化为UINT64。
算法缺点:
(1)实现复杂。
(2)每匹配一个数字都要进行一次内存访问。克服的办法是采用路径压缩,将无分支的路径压缩成一条边,只有真正产生区分的数字才分裂出节点,如图3所示。

图3 路径压缩示例图
4 结束语
虽然在理论上使用字典树数据结构进行前缀查找非常有效,但实际应用中由于其实现的复杂性,同时由于需要分配大量固定长度的节点,会使标准的堆空间分配(如C++中的new)遭受性能和空间上的双重损失,因此如果在查找时间要求不是太苛刻的情况下,二分查找法是比较通用和简便的算法,该算法目前已在实验系统中实现,查询效率比较理想,在1 000多万条电话号码的黑名单中,查询给定的号码所需时间小于0.5 s,但还需要在实际应用中继续完善。本文所述的算法还可以应用在IP地址前缀匹配、身份证号码前缀匹配等问题中。
[1] 刘春煌. 铁道部客票中心系统的设计与关键技术的实现[J].中国铁道科学,2001,22(2):15-22.
[2] 唐 堃.中间件技术在客票系统中的实现及应用[J].中国铁道科学,2004,25(3):103-107.

