基于L2性能准则的双目视觉伺服控制器设计

邹立颖，苗凤娟，陶佰睿，朱 磊

（1.齐齐哈尔大学 通信与电子工程学院，齐齐哈尔 161006；2.齐齐哈尔大学 计算中心，齐齐哈尔 161006）

基于L2性能准则的双目视觉伺服控制器设计

邹立颖1，苗凤娟1，陶佰睿2，朱 磊1

（1.齐齐哈尔大学 通信与电子工程学院，齐齐哈尔 161006；2.齐齐哈尔大学 计算中心，齐齐哈尔 161006）

视觉伺服是利用视觉传感器获得目标物体的图像信息作为反馈信号，对机器人进行闭环控制[1]。与传统的机器人控制相比，视觉伺服控制具有较高的灵活性、精确度以及较强的鲁棒性[2]，使得机器人的智能化程度得到较大幅度的提高。目前，它已成为机器人研究领域的热点之一[3]，并且在很多领域得到了成功的应用。

一般来说，摄像机参数标定误差、摄像机径向畸变、机器人模型误差等不确定性对视觉伺服系统的控制性能会产生不利的影响[4]。

为解决上述不确定性对图像特征产生的影响，考虑手眼机器人双目视觉伺服系统控制对象，本文利用L2性能准则设计理论提出一种新的控制方法。对于文[5]中双目视觉模型，提出了具有L2性能的双目视觉伺服控制器，使得机械手能够渐近收敛到期望位置，同时保证系统全局渐近稳定，使系统对于干扰具有鲁棒性，此外，采用的双目视觉模型无需获取视觉系统的深度信息[3]，也不需要物体的几何模型知识，改善了系统的控制性能，给出的仿真结果验证了该方法的优越性。

1 双目视觉模型

令CP= [X,Y,Z]T为物点坐标，u= [vTΩT]T为机械手末端速度，f为摄像机焦距，B为两摄像机光轴距离，双目立体视觉模型为[5]：

物体上特征点mi=[xyq]T的图像速度，与控制u=[vTΩT]T的关系为：

其中Ji(mi)为特征点mi的图像雅可比矩阵；

具有n个特征点的物体的不确定性双目视觉伺服系统状态方程

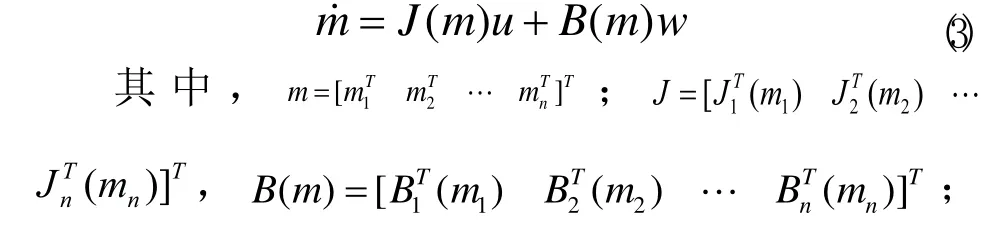
w—等值干扰输入信号，w∈L2。

定义输出评价方程：

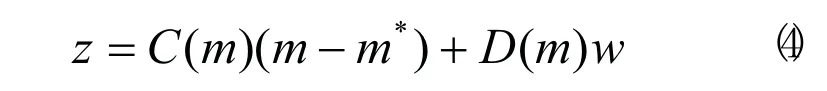
式中：z—输出向量，C(m)、D(m)—系数矩阵。

由式(3)、式(4)得到系统状态方程：

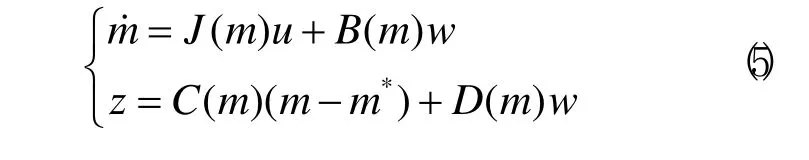
2 具有L2性能的视觉伺服控制器设计

2.1 g耗散的定义

2.2 L2性能准则设计

由于系统的g耗散性与L2性能之间关系是等价的[8]。L2性能准则设计问题可以叙述如下：对于给定的系统(5)，设计控制器u，使得闭环系统对任意正数g，满足如下性能准则：

1)当w= 0时，闭环系统在m=m*是渐近稳定的。

2)存在半正定的光滑存储函数U满足式(6)。

3)闭环系统在图像平面期望特征点m*是可检测的，即当z→ 0 时，m→m*。

那么系统是g耗散的，系统具有L2性能。

定理1：考虑系统式(5)，假设w= 0，给定半

证明：w= 0时，式(5)变为：

由式(5)和式(8)可知，当u=0，z= 0时，必有m→m*，则m*是可检测的。

对于给定的V(m)，沿着系统(9)的状态轨迹，有：

由于J(m)JT(m)是正定的，则V˙≤0，根据La Salle不变集原理得，m*是该系统渐近稳定的平衡点。

定理2：考虑由系统(5)和控制律(7)构成的闭环系统，对于给定的正数g，存在光滑存储函数U(m)使得系统是g耗散的充要条件是：

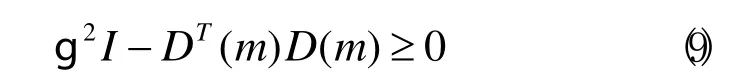
成立，且存在函数向量和矩阵l(m)=G(m)(m−m*)、F(m)满足：

证明： 充分性：考虑如下定义的存储函数：

假设存在l(m)=G(m)(m−m*)、F(m)满足式(10)，对 ()U m进行微分，有：

必要性：设系统式(5)对于光滑可微的存储函数式(11)是g耗散的，即：

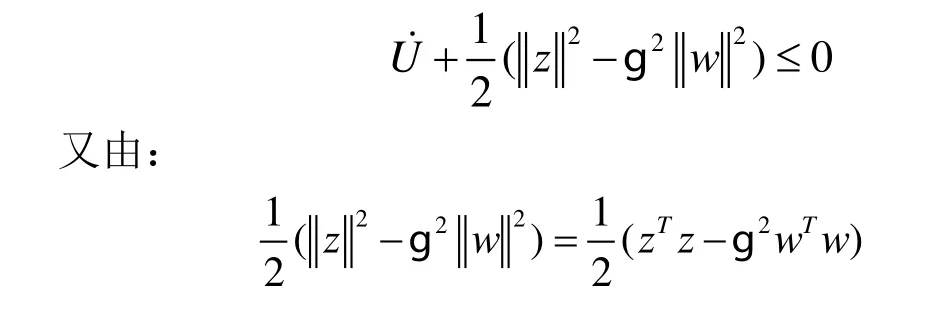
把式(4)代入上式，有：

因此，沿系统的任意轨迹有：

上式的右端是关于w的二次函数，故存在适当的函数矩阵或向量F(m)和l(m)=G(m)(m−m*)，使得：

成立。比较上式等号两端，可知式（10）成立。必要性得证。因此，系统是g耗散的，系统具有小于等于g的L2增益。

以上理论分析表明由本文提出的设计方法能够使机械手稳定地收敛到期望位置，解决了视觉伺服系统的干扰抑制问题。

3 仿真实验

选取一个立方体的八个顶点作为特征点，起点的刚体原点坐标为[22cm;22cm;120cm]，终点坐标为[-6cm;-6cm;60cm]， g = 1，噪声干扰假设为w(t)= 0.002sin(10t)，采样周期为0.1s，图像特征点初始坐标为：

对应的期望坐标为：

仿真结果如图1-图3所示，图1为特征点的图像平面运动轨迹，图2为机械手末端速度曲线，图3为特征点图像误差曲线。可以看出，在存在不确定性干扰的前提下，所设计的控制器能够使当前图像特征渐近收敛于期望图像特征，图像误差逐渐趋近于零，即机器人运动到期望位置。机器人末端速度曲线快速稳定收敛。

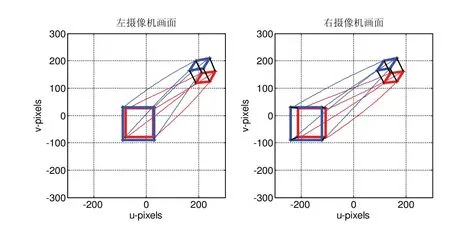
图1 左右摄像机平面特征点运动轨迹

图2 机械手末端速度曲线

图3 图像特征点误差曲线

4 结论

针对基于双目视觉的手眼机器人视觉伺服系统定位问题，考虑不确定性对图像特征产生的影响，首次将非线性理论中L2性能准则理论与双目视觉模型相结合，提出了视觉伺服控制器，能够使机械手稳定地收敛到期望位置，解决了视觉伺服系统的干扰抑制问题。理论分析和实验均证明了该方法具有全局渐近稳定性和鲁棒性，快速性等控制性能。此外，由于所采用双目模型无需获取视觉系统的深度信息，也不需要物体的几何模型知识，改善了系统的动态性能。

[1]Seth Hutchinson, Gregory D. Hager, and Peter I. Corke.A tutorial on visual servo control[J].IEEE Trans.Robot.Automat.,1996,12(10): 651-670.

[2]王麟琨,徐德,谭民.机器人视觉伺服研究进展[J].机器人,2004,26(3):277-282.

[3]邹立颖,李惠光.基于新双目模型的变结构视觉伺服控制方法[J].武汉理工大学学报,2009,31(10):117-120.

[4]C.Wang,Y.Shen,Y.Liu,and Y.Wang. Robust Visual Tracking of Robot Manipulators with Uncertain Dynamics and Uncalibrated Camera.7th Int. Conf. on Automation,Robotics and Vision, Singapore,2002:1144-1149.

[5]Huiguang Li, Mei Jin, Liying Zou.A New Binocular Stereo Visual Servoing Model[C].IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application,2008:461-465.

[6]Kiihnlenz, K.;Buss,M.Towards multi-focal visual servoing.Intelligent Robots and Systems,2005.(IROS 2005). 2005 IEEE/RSJ International Conference on. 2-6 Aug. 2005 Page(s):3289-3294.

[7]Comport,A.I; Marchand, E; Chaumette, F. Statistically Robust 2-D Visual Servoing. Robotics, IEEE Transactions on.Volume 22,Issue 2,April 2006 Page(s):415-420.

[8]金梅,李惠光,邹丽颖,武波.具有L2性能的视觉伺服控制器设计[J].系统仿真学报,2009,21(13):4101-4105.

Design of binocular visual servoing controller based on L2performance rule

ZOU Li-ying1，MIAO Feng-juan1，TAO Bai-rui2，ZHU Lei1

考虑手眼机器人双目视觉伺服控制干扰抑制问题，本文利用L2性能准则设计方法提出一种新的控制方法。针对手眼机器人双目视觉伺服系统控制对象，提出了具有L2性能的双目视觉伺服控制器，使得机械手能够渐近收敛到期望位置，使系统对于不确定性具有鲁棒性。同时，证明了系统具有全局渐近稳定性，采用的双目视觉模型无需获取视觉系统的深度信息，改善了系统的动态性能。最后，给出的仿真结果验证了所提出方法的优良性能。

视觉伺服；L2性能准则；双目视觉；手眼系统；全局稳定

邹立颖（1980 -），女，黑龙江林甸人，讲师，硕士，研究方向为机器人视觉伺服控制、智能控制和非线性控制。

book=16,ebook=76

TP242

A

1009-0134(2014)04(下)-0039-03

10.3969/j.issn.1009-0134.2014.04(下).11

0 引言

2014-01-23

黑龙江省自然科学基金（F201332）；黑龙江省普通高等学校新世纪优秀人才培养计划（1253-NECT025）