机车牵引齿轮齿根强度有限元分析

董淑婧

（大连科技学院 机械工程系，大连 116052）

机车牵引齿轮齿根强度有限元分析

董淑婧

（大连科技学院 机械工程系，大连 116052）

0 引言

渐开线齿轮传动作为一种重要的机械传动方式，广泛应用于车辆、矿山及纺织等领域，在机车上常被用作牵引装置，作为整个传动装置的核心部分，机车牵引齿轮是使机车通过牵引电机电枢轴传递动力而使车轮转动的重要部件[1]。随着机车向高速、重载方向发展，对机车牵引齿轮提出了越来越高的要求，不仅要求牵引齿轮所传递的功率越来越大，转速越来越高，而且又要具有尽可能高的使用寿命和承载能力，为了满足上述要求就必须对齿轮的各项强度指标进行准确的分析计算。但是对于运行于高速重载条件下的机车牵引齿轮若只采用传统的的计算方法已不能满足其计算精度要求，因此本文采用有限元方法对主从动齿轮的齿根强度进行了计算和分析。

1 机车牵引齿轮的有限元模型

1.1 机车牵引齿轮基本参数

机车牵引齿轮主从动轮的基本几何参数如表1所示，机车牵引齿轮的在各工况下的载荷大小如表2所示。

表1 齿轮基本参数表

1.2 齿轮传动系统结构参数

根据主从动齿轮的基本几何参数及其对应轴段的结构尺寸，所建立主从动齿轮的实体模型分别如图1和2所示。

1.3 有限元网格的划分

分别对主动齿轮、从动齿轮进行有限元网格的划分[2]。如图3～图4所示，其求解规模为：

主动齿轮：空间块体单元总数474840；结点总数569037；

表2 机车牵引齿轮载荷参数

图1 主动齿轮实体模型

图2 从动齿轮实体模型

图3 主动齿轮有限元网格图

图4 大齿轮局部结构有限元网格图

从动齿轮：空间块体单元总数 522451，结点总数554646。

1.4 设置分析条件

1）分别对大小齿轮在三种工况条件下的载荷大小进行了计算，具体载荷计算数据如表2所示。

2）加载节点位置分析：通过综合分析，在进行加载节点位置的确定上，主要考虑两种载荷危险情况，具体分析结果如下。

（1）方案一：啮合齿对接触线经过齿轮端面齿顶加载方案

加载节点的位置确定主要考虑使齿根危险截面上的弯曲应力最大；由一对齿轮啮合过程可知，当其中一对轮齿的接触线经过某个轮齿端面齿顶时，此时，对应的弯曲力臂最长，可作为一种危险工况进行加载。

由斜齿轮的啮合原理可知：一对斜齿圆柱齿轮在啮合过程中，其齿面间的接触线为一组位于两轮啮合面内相互平行的斜直线，接触线的倾斜方向与两轮轴线的夹角为基圆螺旋角bβ。根据几何关系，绘制出加载节点位置尺寸确定示意图如图5所示。图中所示的矩形区域 B1B2B′2B1′为一对齿轮的实际啮合区，建立以终止啮合点B1为原点，以端面实际啮合线B1B2方向为X轴，齿宽b方向为Y轴的坐标系，其正方向如图5所示。根据计算，当一对轮齿在齿顶接触时，齿轮工作在图5阴影部分所示的双齿区，两对轮齿均为全齿宽接触，而且，两对轮齿在端面上相距一个基圆齿距Pbt。以确定主动轮加载下节点半径；而此时，两轮齿加载上节点均为各自齿顶圆。

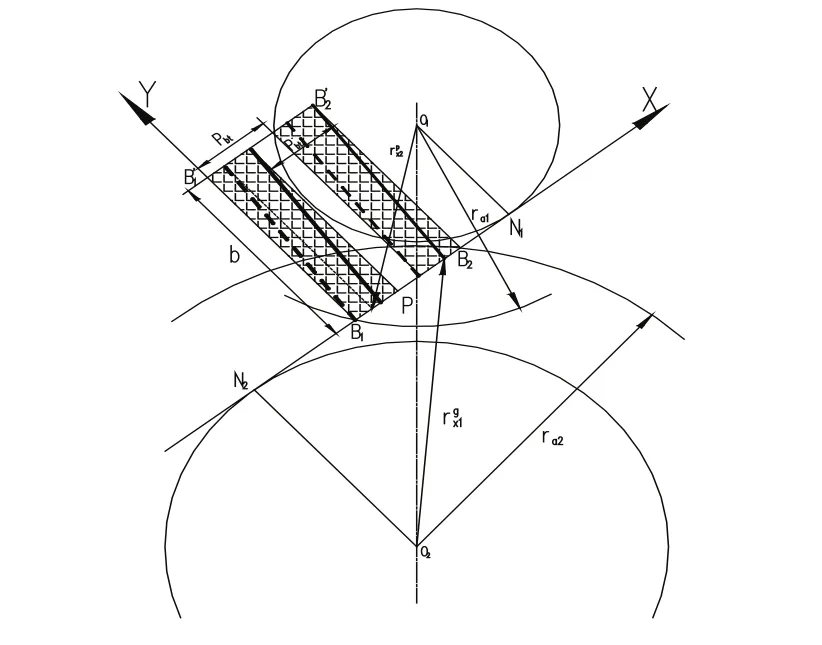
图5 方案一接触线分布及加载节点半径范围确定图

在此种条件下，由于两对齿均为全齿宽参与啮合，所以在分配载荷时，可以认为单对齿轮的啮合力为总载荷的一半，即取总载荷的50%作为计算载荷进行节点力的施加。

（2）方案二：接触线总长度最短工况对应加载方案

由于齿向倾斜，主从动齿轮在啮合过程中的接触线总长度随着啮合位置的变化而变化。当接触线总长度最短，既单位齿宽上的载荷最大时，此种情形为两轮齿啮合过程中的另一危险工况。

由计算结果可知，齿轮的总重合度大于2，所以至少有两对齿同时参与啮合，即存在双齿和三齿啮合区。啮合区1221BBBB′′内轮齿间的啮合情况简要概述为：根据实际计算和理论分析结果，两齿轮在啮合过程中接触线总长度虽然发生变化但并不连续。当两对齿全为全齿宽接触时接触线总长度最长；此后，随着各对轮齿沿图5中X轴负方向逐渐通过啮合区的过程中，靠近啮合终点B1的一对齿（第一对齿）逐渐退出啮合区，接触线总长逐渐变短；直到第二对齿到达小齿轮的端面单齿啮合区的上界点D时，第三对齿开始逐渐进入啮合区，从此，第一对齿缩短的接触线长度与第三对齿增加的接触线长度相等，接触线的总长度保持不变，并且在整个啮合过程中最短，如图6中虚线所示；最后，当第一对齿完全退出啮合，第二对齿完全进入大齿轮端面单齿啮合区上界点E时，如

图6 方案二接触线分布及加载节点半径范围确定图

通过软件编程计算，当啮合点分别经过两齿轮端面单齿啮合区的上界点D、E时接触线长度最短，其中一对轮齿为全齿宽接触，其余接触轮齿只有部分齿宽接触，通过计算接触线总长度为233.8449mm，全齿接触的一对齿的接触线长度占总接触线长度的72.85%，所以载荷分配时按此比例进行节点载荷的施加。具体加载位置如表3所示。

3）约束的施加，对于小齿轮由于结构尺寸较小，所以采用整个齿轮进行有限元计算。因此，约束的施加为：对图3中的齿轮伸出轴段端面上的所有节点施加三个坐标轴的位移约束，形成小齿轮的悬臂梁受力结构。

对于大齿轮：由于齿轮的模型较大，所以对模型进行了简化。选择了大约对应30o圆心角范围内的10个轮齿进行建模，并导入到软件中形成有限元模型，如图4所示。约束的施加：在齿轮轴心处生成刚性节点单元然后与齿轮轴孔内表面的所有节点进行刚性耦合，并在该刚性节点上施加所有方向上的约束。

2 有限元计算结果

在有限元分析软件ANSYS中通过对所建立的主从动齿轮的有限元模型进行分析计算，得到主从动齿轮齿根部的第一主应力的最大值，第二主应力的最大值，第三主应力的最大值以及von Mises应力最大值如表4所示。

表3 加载节点位置参数

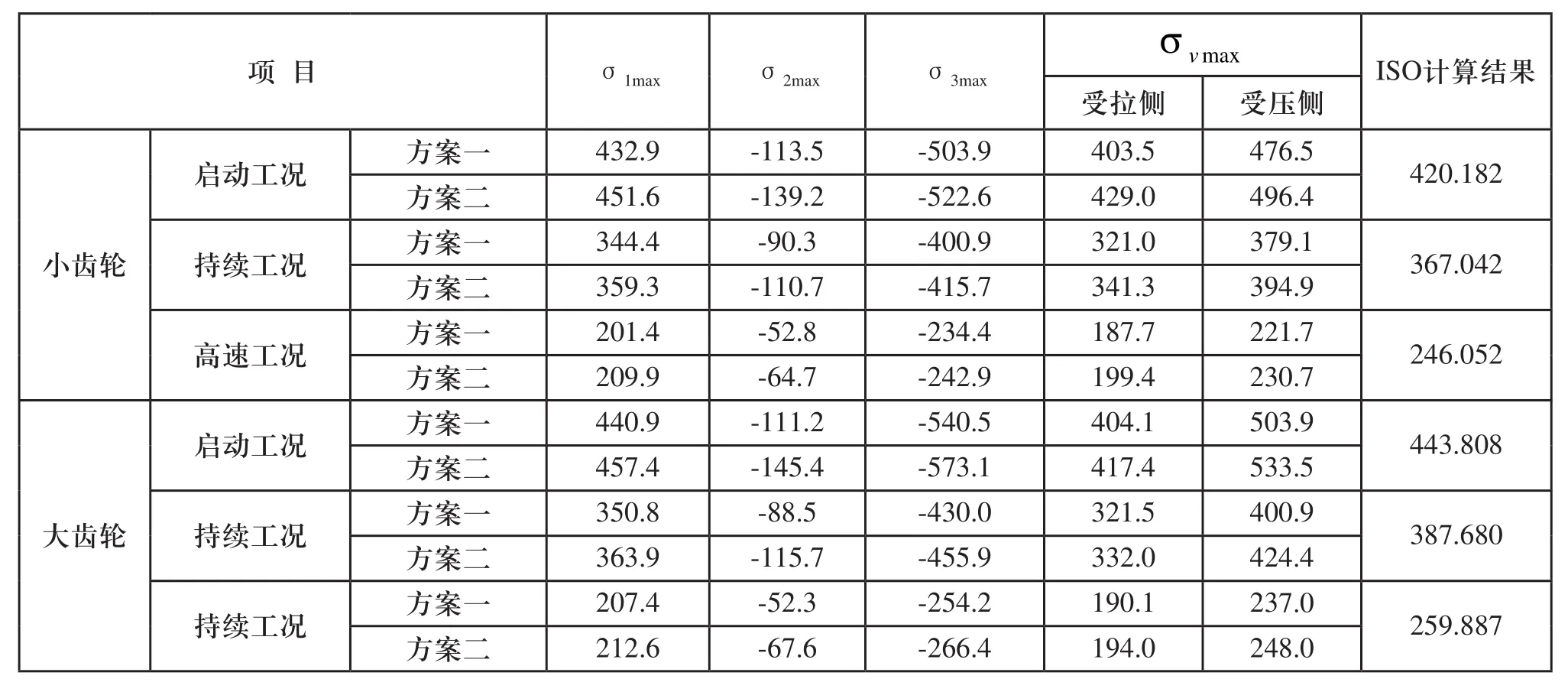
表4 交流传动电力机车牵引齿轮齿根应力有限元计算结果(MPa)

主从动齿轮在启动工况下对应加载方案一的应力分布情况如图7、图8所示，其他工况条件下，应力分布规律基本相同，只是数值上逐渐减小。

图7 小齿轮启动工况总体应力云图

3 结论

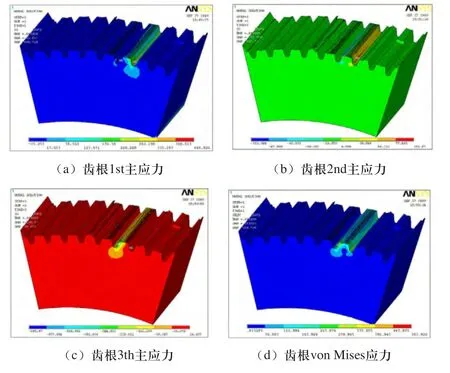
图8 大齿轮启动工况总体应力云图

分析主从动齿轮齿根强度有限元计算结果及ISO[3]计算结果，大齿轮的齿根应力均比小齿轮应力值大，主要原因为小齿轮采用正变位，而大齿轮采用负变位，同时对于方案二的计算结果，虽然加载位置有所降低，但施加在节点上的载荷较方案一增加了45.7%，所以计算得到的应力值均较方案一有所增加。

[1]鲍君华,何卫东,李力行.高速机车牵引齿轮的参数化实体建模及其动力学分析[J].机械传动,2009:70-72.

[2]龚曙光.ANSYS工程应用实例解析[M].北京:机械工业出版社,2003.

[3]闻邦椿.机械设计手册[M].北京:机械工业出版社.2010.

Finite element analysis of the traction gear tooth root intensity

DONG Shu-jing

本文基于有限元分析软件ANSYS建立了机车牵引齿轮主从动齿轮的有限元模型，通过两种加载方案对模型进行了分析计算，得到主从动齿轮的弯曲应力，为了验证模型的正确性，通过ISO标准对主从动齿轮的弯曲强度进行了理论计算，并对最终的有限元计算结果进行了静态分析。

齿轮；有限元；强度

董淑婧（1981 -），女，山西省应县人，讲师，硕士，研究方向为机械设计。

TH132

A

1009-0134(2014)06(上)-0034-04

10.3969/j.issn.1009-0134.2014.06(上).09

2014-03-18