动态负压计算模型建立及其相关因素分析

常鹏刚, 王永清, 范生林, 蒋睿, 张彦杰

(1.西南石油大学油气藏地质及开发工程国家重点实验室, 四川 成都 610500;2.中国石油川庆钻探工程有限公司钻采工程技术研究院, 四川 广汉 618300)

0 引 言

随着大量特殊油气藏的开发,如低压力、低渗透率、致密性油气藏,采用常规静态负压射孔技术无法得到理想的产能。为了解决这一难题,斯伦贝谢公司提出了动态负压射孔技术,该技术在射孔爆轰时,能够在井筒内快速形成负压差[1-4],瞬间释放地层能量,使射孔孔眼产生幅度更高、持续时间相对更长的泄流,从而有效清除射孔污染,提高油气井的产能。

但是,到目前为止,人们对动态负压作用机理及其变化特征的认识还存在较大争议,无法使其量化成为一个动态负压计算模型,有必要进行相关因素对比分析[5-16]。据此,本文运用相关数学推演方法建立一个考虑因素较为全面的动态负压计算模型。利用相关数据,对模型的正确性和实用性进行了验证,并且利用该模型对相关影响因素进行了对比分析。

1 动态负压计算模型建立

通过研究发现,动态负压值的大小与井筒初始压力、射孔枪装药量、泄压腔体积大小、储层泄流幅度等因素相关。设原始地层压力为pi;井筒射孔段初始压力为p1;地层泄流引起的井筒压力回升为p2;泄压腔泄流引起的井筒压力降落为p3;爆轰之后气体膨胀引起的井筒压力波动为p4,则可以列出某一时刻计算动态负压值的基本公式

pD(t)=p1+p2-p3+p4

(1)

1.1 地层泄流引起的压力回升值p2的计算

动态负压射孔射孔枪起爆后,井筒与储层之间的压力差引起储层瞬间泄流,泄流的幅度刚开始逐渐增大,达到最大值之后又逐渐减小,泄流流量随时间的变化关系近似满足

Q(t)=-at2+bt(a>0)

(2)

则在某一时刻t,则有

Q(t)t=-at3+bt2

(3)

(4)

通过上面的推导,可以得到地层泄流引起的井筒压力变化率的表达式。在单纯储层泄流作用的影响下,井底压力随时间的变化关系为

(5)

又因为t=0时,p2=p1,所以,通过积分可得

(6)

按照实际情况,当地层泄流流量变为0时,井筒压力应该保持某一恒定值,不再发生变化。但是,在公式(6)中,当储层泄流流量变为0时,井筒压力反而有一个明显的下降趋势,这与实际情况不相符,所以有必要对上述公式进行修正。为此引入泄流截止时间的概念。为了得到泄流截止时间,令Q(t)=0,即有

-at2+bt=0

(7)

解该一元二次方程,可以得到泄流截止时间有意义的解为t=b/a。

利用泄流截止时间将上述公式进行分段表示,以使其与实际工况相符合

(8)

式中,p1为井筒初始压力;ρo为原油密度;h为泄流体积在相同井筒体积内的液柱高度;rw为井筒半径;t为泄流时间;a、b分别为与储层渗透率有关的实验常数。

通过这样的一个修正,就得到了储层泄流引起的井筒压力随时间变化的表达式,在泄流结束之后,井筒压力变化轨迹将始终保持不变。

1.2 泄压腔泄流引起的压力降p3的计算

动态负压射孔时,在泄压腔泄流的过程中可以选择合适的流体截面,运用伯努利方程得到泄压腔泄流引起的压力降p3与时间的变化关系。具体推导过程,首先,选择截面1与2之间的流体为一个系统(见图1),运用伯努利方程则有

(9)

由于,v1A1=v2A2且A1≫A2;所以,v1≈0,vm≈v2。

图1 泄压原理图

如果所选用的泄压腔是真空密封的,那么,p3=0,伯努利方程变为

(10)

化简,得

(11)

(12)

为了增进该计算公式的实用性,将Vo用sV代替,其中s是一个关于时间、枪套间隙、泄压孔孔径等因素的函数,将其命名为降压因子,式(12)变为

(13)

式中,s为降压因子;ρ为射孔液密度;g为重力加速度;A为开孔面积;Vo为某一时刻进入泄压腔内的流体体积;V为泄压腔体积;H为井筒内射孔液柱高度;t为时间;vm为平均流速;dc为冲孔弹冲孔直径;p0为井口压力。

因此,在泄压器单纯作用下,井筒压力随时间变化的完整表达式为

(14)

式中,ζ为局部损失系数,取0.05。

1.3 爆轰气体膨胀引起的压力回升值p4的计算

为了进一步了解枪内爆炸与燃烧过程,中国某学者利用实验室单发射孔单元模拟套管试验装置及动态测试技术的方法,对装有某种火药的102复合射孔器进行了枪内和环空p-t测试。通过对其试验结果的分析,利用Matlab软件进行了数据拟合,得到公式

p(t)=68.96e-0.1471t-68.77e-3.148t

(15)

通过换算得到了单位质量装药量下井筒环空压力随时间的变化关系。当装药量为mg时,又因为复合射孔器与一般常规射孔器相比,二者在结构上存在较大差异,所以,再应该给p(t)乘以一个比例系数c,才能较真实地反映在动态负压射孔条件下,井筒压力随时间变化的情况。即在动态负压射孔时,井筒环空压力随时间变化的关系式

(16)

至此,将p1、p2、p3、p4代入式(1)中,通过相应的化简计算,就建立了计算动态负压大小的基本数学模型。

当t=0时,

pD(t)=p1

(17)

(18)

(19)

式中,a、b、c为常数,

2 动态负压计算模型的验证

为了进一步分析所建立的动态负压计算模型的正确性,假设了1组合理的数据并进行了一次验证和分析。假定pi=30 MPa;rw=6 cm;p1=8.0 MPa;ρo=0.8 g/cm3;g=9.8 m/s2;a=515;b=1.6×104;c=0.4;ds=0.8 cm;ρ=1.1 g/cm3;Ns=36孔/m;Ls=12 m;s=0.1;dc=2.4 cm;dq=8.9 cm;Nc=12个;Lc=12 m;dx=8.9 cm;m=400 g。其中,dq为射孔枪端口直径;dx为泄压腔端口直径;Ls为射孔枪长度;Lc为泄压腔长度;ds为枪身孔眼直径;dc为泄压孔直径;Nc为泄压孔个数;Ns为孔密。

在上述各参数假定值下,首先绘制了单因素条件作用下井筒压力的变化曲线(见图2),各曲线趋势以及大小幅度都符合当初的设想。图3为动态负压变化曲线。从图3中可以看到,在17 ms左右,实现了最大动态负压差8 MPa。

该计算结果充分证明了我们所建立的动态负压计算模型的正确性和实用性。

图2 单因素条件作用下井筒压力变化曲线

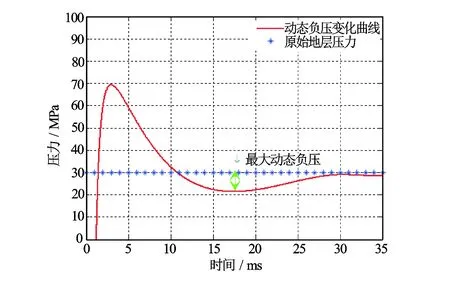
图3 动态负压变化曲线

3 动态负压相关影响因素对比分析

3.1 降压因子对动态负压大小及其持续时间的影响

降压因子本身是一个影响因素非常繁杂的多元函数,在短时间内无法获得其因素考虑较为全面的解析表达式,并且,降压因子也不是本文讨论的重点,所以,近似地将降压因子看作一个常数,分析其对动态负压幅度大小及其持续时间的影响。不同降压因子下的动态负压变化曲线如图4所示。从图4中可以直观看到,随着降压因子的增大,动态负压幅度及其持续时间都将增大。这也间接说明了合适的枪套间隙、泄压孔直径、布孔方式等因素对动态负压大小及其持续时间的重要影响。

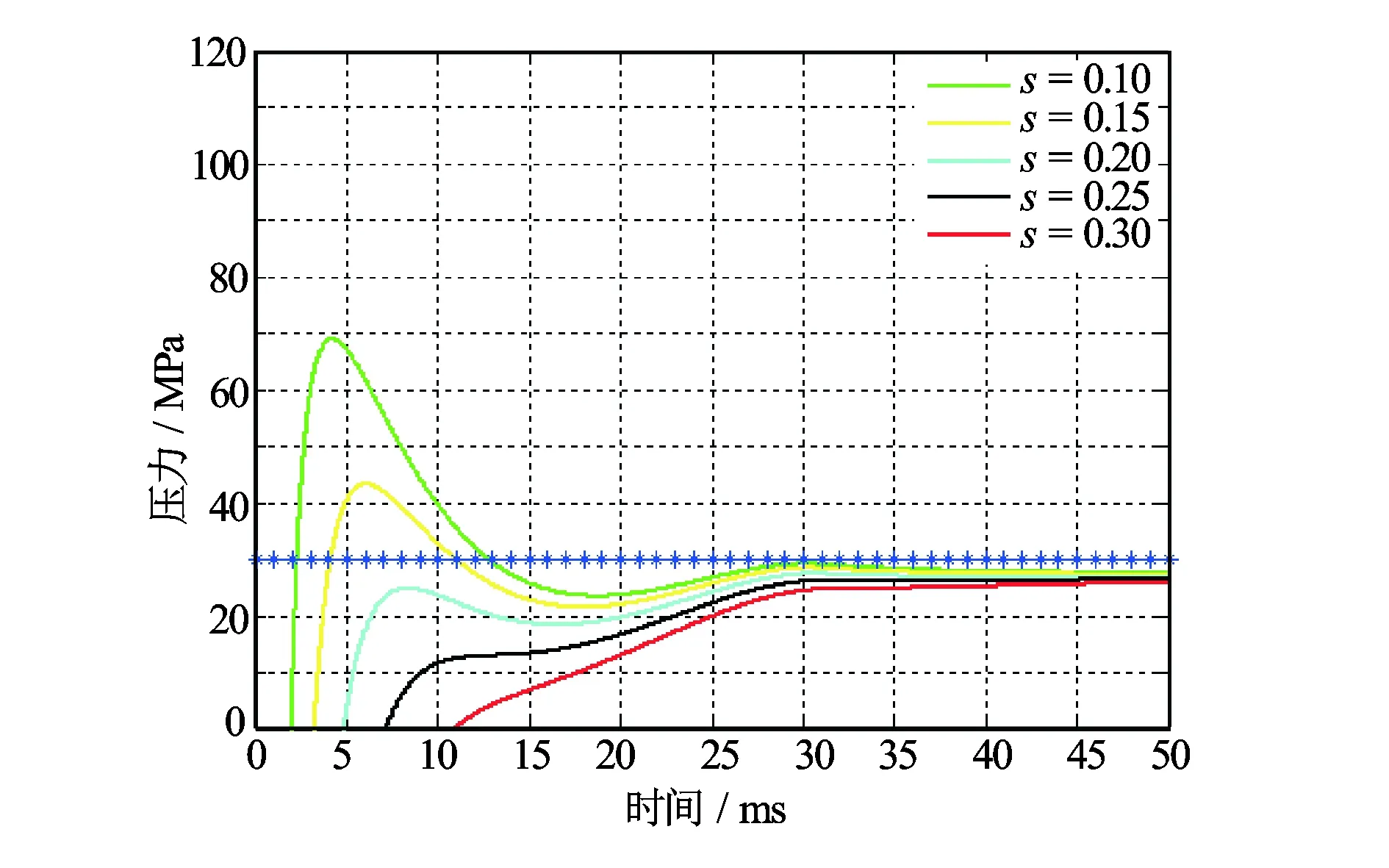
图4 不同降压因子时动态负压变化曲线

3.2 系数c对动态负压大小及其持续时间的影响

比例系数c体现的是常规动态负压射孔器与复合射孔器之间的差异程度,不同的c对动态负压幅度大小及其持续时间的影响见图5。从图5中可以看到,随着c的增大,动态负压幅度及其持续时间都将大幅下降。所以,在特定的井筒条件下,选择合适的c值,对成功进行动态负压射孔将产生重要的影响。

图5 不同c时动态负压随时间的变化曲线

3.3 装药量对动态负压大小及其持续时间的影响

不同的装药量对动态负压幅度大小及其持续时间有着巨大的影响(见图6)。随着枪身装药量的增加,射孔爆轰时的正压幅度及其持续时间都将增大,这大大减弱了动态负压幅度的大小及其持续时间。

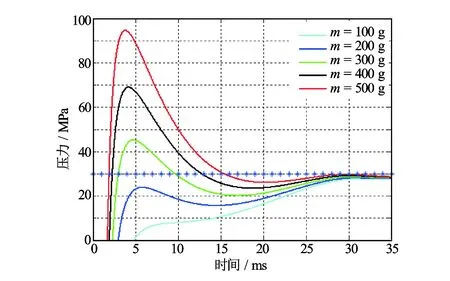
图6 不同装药量时动态负压变化曲线

3.4 泄压器长度对动态负压大小及其持续时间的影响

不同的泄压器长度对动态负压幅度大小及其持续时间也有显著的影响(见图7),随着泄压器长度的增加,动态负压幅度及其持续时间都将相应的增大。在相同的装药量下,随着泄压器长度的增加,其最显著的特点是大大减弱了井筒残余爆轰能量的幅度和持续时间。

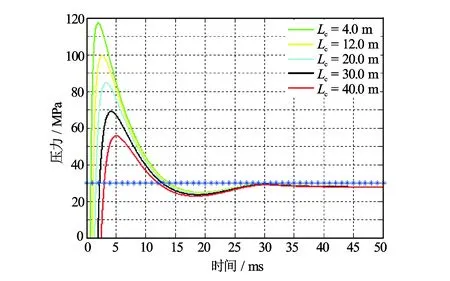
图7 不同泄压器长度时动态负压变化曲线

3.5 孔密对动态负压大小及其持续时间的影响

射孔孔密是一个重要的射孔参数,其对动态负压幅度大小及其持续时间也有着较大的影响(见图8)。随着射孔孔密的增加,动态负压幅度及其持续时间都会减小。随着孔密的增加,泄压面积增加,这在一定程度上会增大动态负压幅度及其持续时间,但是,它也增大了射孔枪内残余爆轰能量向井筒转移的面积,二者综合作用的结果,表现出来的为动态负压幅度及其持续时间的减小。这个结论与不同泄压面积时的动态负压变化规律完全一致(见图9)。而与射孔孔密相对应的泄压孔个数则对动态负压大小及其持续时间的影响较小。

图8 不同孔密时动态负压变化曲线

图9 不同泄压面积时动态负压变化曲线

3.6 孔径对动态负压大小及其持续时间的影响

图10为不同孔径下的动态负压变化曲线,从图10可见,孔径对动态负压幅度大小及其持续时间的影响较小,但是,孔径对射孔爆轰之后井筒正压幅度的影响却很大。这也从另一方面证明了泄压面积的增大,使动态负压幅度及其持续时间减小的结论。而与其相对应的泄压孔孔径则对动态负压大小及其持续时间的影响较小。

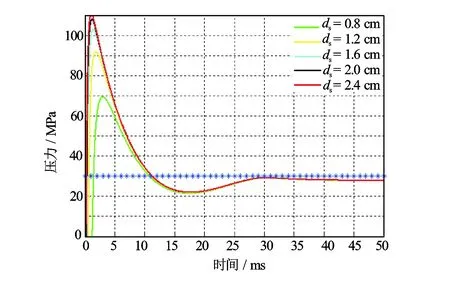
图10 不同孔径下动态负压变化曲线

3.7 泄压面积和泄压体积对动态负压大小及其持续时间的影响

泄压面积和泄压体积是2个宏观因素,它们本身包含了诸如孔密、孔径、枪身长度等单因素。分析其对动态负压幅度大小及其持续时间的影响,实际上是分析在多因素共同作用下动态负压幅度大小及其持续时间的变化规律。由图9和图11可知,随着泄压面积的增加动态负压幅度及其持续时间均相应的减小,随着泄压体积的增加动态负压幅度及其持续时间均相应的增大。

在后续的进一步研究中,我们还发现动态负压射孔时井筒内射孔液密度对动态负压幅度大小及其持续时间基本没有影响。

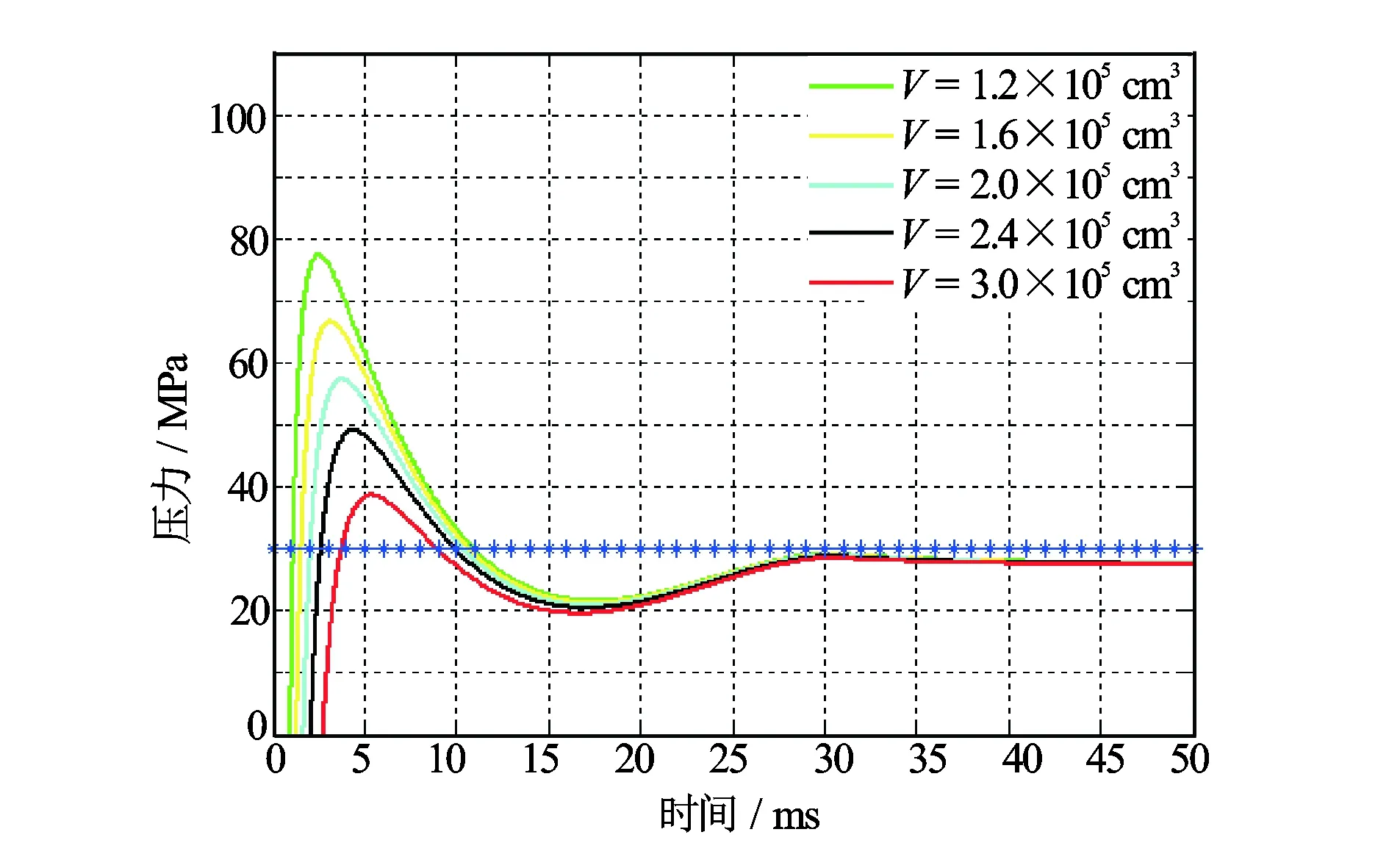
图11 不同泄压体积时动态负压变化曲线

4 动态负压射孔与静态负压射孔井筒动态对比

如果将建立的动态负压计算模型作稍微改动,就得到了静态负压射孔时井筒压力变化的计算模型,见式(20)和式(21)。在相同的设计参数假定值下,绘制动态负压射孔与静态负压射孔井筒动态对比曲线(见图12)。

图12 动态负压与静态负压对比曲线

从图12中可以看到,动态负压射孔时的井筒负压幅度及其持续时间均比静态负压射孔时的井筒负压幅度及其持续时间大得多。在射孔爆轰瞬间,静态负压射孔时的井筒正压幅度远远高于动态负压射孔时的井筒正压幅度,而且静态负压射孔还可能出现使井筒压力始终为正的状态。这充分证明了动态负压射孔技术的优越性和合理性。

(20)

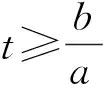
(21)

式中,a、b、c为常数。

5 结 论

(1) 利用相关数学方法建立了动态负压计算模型和静态负压计算模型。

(2) 提出了泄流截止时间和降压因子的概念,并且分别对其进行了系统的分析与计算。

(3) 对比分析了各相关因素对动态负压大小及其持续时间的影响程度。随着降压因子的增大,动态负压幅度及其持续时间都将增大;选择合适的c值,对成功进行动态负压射孔将产生重要的影响;装药量对动态负压幅度大小及其持续时间有着巨大的影响;随着泄压器长度的增加,动态负压幅度及其持续时间都将相应的增大,并且增加泄压器长度也减弱了井筒残余爆轰能量的正压幅度;泄压孔孔径对动态负压幅度大小及其持续时间的影响较小;随着射孔孔密的增加,动态负压幅度及其持续时间都会减小;孔眼孔径对动态负压幅度大小及其持续时间的影响较小,但是,孔径对射孔爆轰之后井筒正压幅度的影响却很大;射孔液密度对动态负压幅度大小及其持续时间基本没有影响;随着泄压面积的增加动态负压幅度及其持续时间均相应的减小,随着泄压体积的增加动态负压幅度及其持续时间均相应的增大。

(4) 进行了动态负压射孔与静态负压射孔井筒动态的对比,证明了动态负压射孔的优越性和合理性。

参考文献:

[1] Eelco Bakker, Kees Veeken, Lamy Behrmann. 动态负压射孔新技术 [J]. 国外测井技术, 2004, 19(5): 48-60.

[2] 刘桥. PURE动态负压射孔技术在大庆油田的应用 [J]. 应用科学, 2009, 18: 150.

[3] 刘方玉, 刘桥, 蔡山. 动态负压射孔技术研究 [J]. 测井技术, 2010, 34(2): 193-195.

[4] 李东传, 金成福, 刘桥等. 聚能射孔器爆炸气体损害机理研究 [J]. 测井技术, 2011, 35(5): 494-496.

[5] Humberto Campos, Sergio Martinez. Geomechanical Applications for Near-balance and Dynamic Underbalance Perforating Technique in Overpressured Gas Zones in Burgos Basin [C]∥SPE108480, 2007.

[6] Martin A J, Clark D, et al. Dynamic Underbalanced Perforating on a Mature North Sea Field [C]∥SPE93638, 2005.

[7] Medina M, Moranes G, et al. Dynamic Underbalanced Perforating Application Increases Productivity in the Mature High-permeability Gas Reservoirs of Santa Ana Field, Venezuela [C]∥SPE112488, 2008.

[8] Tovar J, Appleby R. Design and Evaluation of Perforation Performance Using Dynamic Under Balance-North Sea Case Histories [C]∥SPE135712, 2010.

[9] Minto D, Falxa P, Manalu D. Dynamic Underbalanced Perforating System Increases Productivity and Reduces Cost in East Kalimantan Gas Field: A Case Study [C]∥SPE97363, 2005.

[10] Al-Marri Faisal, Hassan Ibrahim Khalil. New Perforating Technique Improves Well Productivity and Operational Efficiency [C]∥SPE101278, 2006.

[11] Dennis Baxter, et al. Overcoming Environmental Challenges Using Innovative Approach of Dynamic Underbalance Perforating [C]∥SPE108167, 2007.

[12] Bahrami H, Siavoshi J, Sheikh Veisi M. Numerical Simulation of Wellbore Dynamics During Underbalanced Perforation [C]∥SPE120162, 2009.

[13] Bolchover P, Walton I C. Perforation Damage Removal by Underbalance Surge Flow [C]∥SPE98220, 2006.

[14] Walton I C. Optium Underbalance for the Removal of Perforation Damage [C]∥SPE63108, 2000.

[15] Grove B, Harvey J, Zhan L. Perforation Cleanup via Dynamic Underbalance: New Understandings [C]∥SPE 143997, 2011.

[16] Russell L Detwiler, Joseph P Morris, Ozgen Karacan C. Evaluation of the Relative Importance of Parameters Influencing Perforation Cleanup [C]∥SPE 86538, 2004.