EMD与ICA在故障诊断中的应用研究

宋玉标，许宝杰，吴国新，左云波

（北京信息科技大学 现代测控教育部重点实验室，北京 100192）

0 引言

信号是信息传递的载体，为了从现实测量的振动信号中提取各种有用信息，必须采取各种有效的信号处理方法进行处理，从而进行后期信号的状态监测和故障诊断等内容，振动信号的处理方法已成为科学研究的热点之一[1]。但是通过现有数据采集系统所得到的振动信号包含各种噪声，必须经过有效方法处理噪声信号，提高信噪比，提取淹没在噪声信号中的有用信息，才能够获取正确的特性信息。在过去的信号处理方法中，特征向量的准确提取往往依赖于采集信号的平稳性，信号的固有特性只能从时域或者频域中表示出来，不能在时域和频域的同一时间内反映出信号的局部化特点。机电装备的复杂机械运转信号往往多是非线性和非平稳性的，针对这些特征信息的处理方法一直是国内外研究的难题。而对于机电设备故障频发和外部干扰很强时，针对微弱特征信号的提取传统方法更是力不从心。

近年来，一些专家和学者提出了各种处理信号的现代方法。Wigner-Ville分布Wigner-Ville distribution，WVD) 是一种重要的双线性时频分布，具有高的时频分辨率能量集中性和满足时频边缘特性等许多优良特性，在一定程度上解决了短时傅里叶变换存在的问题。但是由于Wigner-Ville时频分布为双线性，对于多分量信号而言，WVD存在严重的交叉项干扰，阻碍了其对信号的有效分析和各分量参数的提取，严重影响了信号的检测性能[2]。Donoho等提出了一种基于阈值处理思想的小波降噪方法，小波分析方法是一种窗口大小固定但其形状改变，时间窗和频率窗都可改变的时频局域化分析方法，这种特性使小波变换具有对信号的自适应性，这也正克服了傅里叶变换不能在时域和频域上局域化的缺点[3,4]。但是小波变换和傅里叶变换是有一定的联系的，还是存在窗函数的局限性，频率和时间之间的变化，不能够准确的得到描述。

Nordeng E．Huang等人认为，如果信号是由许多不同的固有模态组成的，每个模态可以是线性的或非线性的; 如果模态之间混叠，它们形成了一个复合信号。固有模态对应的函数称为固有模态函数( intrinsic mode function，IMF) ，浙江大学的杨世锡等人利用基于经验模态分解的希尔伯特变换，证明在旋转机械时频分析中有效性[5,6]。盲源分离问题的提出产生于80年代，随之也产生多种盲源分离算法，其中独立分量分析便是一种新方法。它可以从混合信号中分离出各个单一信号的特征，实现对各信号分量进行分离[7]。本文结合EMD和ICA的优势，提出了一种利用EMD-ICA联合进行特征信号处理的方法，对滚动轴承故障数据进行特征信号提取分析，实验结果验证了该方法的有效性。

1 EMD方法基本思想

EMD方法就是对复杂信号进行筛选的过程，通过对采集的非平稳和非线性数据信息逐级分解，形成一系列稳态的和线性的数据阵列，即固有模态对应的函数，即本征模函数（intrinsic mode function，IMF）。IMF必须满足以下两个条件[8]：

1) 信号时间轴对称性。即在上下两条包络线之间的信号要在任何时候，信号的平均值是0；

2) 信号的极点和零点的轮流交换出现。即零点数和极值点数最多相差1个或者是相等，分解后在每一时刻只有一个频率成分，这样对于瞬时频率来说便拥有了真实的物理意义。

下面给出时间序列数据s(t) 的经验模式分解算法[9]：

1) 初始化：r0(t) = x(t)，i = 1

2) 得到第i个IMF;

(1)初始化：h0(t) = r i (t)，j = 1；

(2)找出hj-1(t)的局部极值点；

(3)对hj-1(t)的极大值和极小值点分别进行 差值处理，形成上下包络线；

(4)计算上下包络线的平均值mj-1(t)；

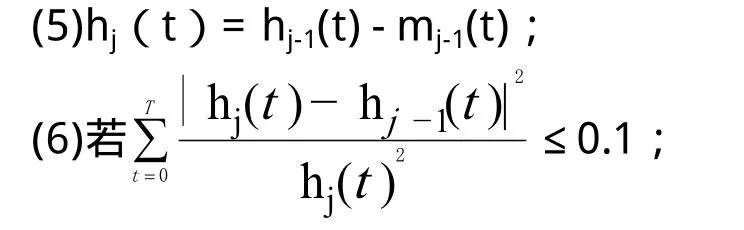
则Iimfi(t) = hj（t）；否则，j = j+1，转到(2)。

3) ri(t) = ri-1(t) - Iimfi(t)，

4) 若ri(t) 极值点数不少于2个，则继续计算，i=i+1，转到2；否则，分解结束，ri(t) 是残余分量。

该算法最后得到的公式为：

即为原始数据可表示为本征模函数分量和一个残余分量。

2 ICA方法基本思想

假设信号源为s(t)它经过未知的混合矩阵A，x(t)为传感器观测到的信号，则盲源分离的模型可以表示为[10]：

上面公式中，x(t) = [x1(t)，x2(t),...,xm(t)]T为M维观测向量，s(t) = [s1(t)，s2(t),...,sn(t)]T，是N维的源信号，它是不可知的，n(t)为M维的噪声信号。基于统计学上相互独立性的源信号满足要求，并且采集信号的维数M同样也满足与源信号s的维数N之间的关系，则盲源分离的整个过程就可表示如下，其关系为：

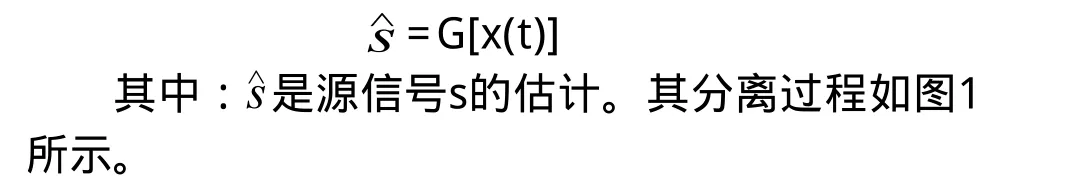
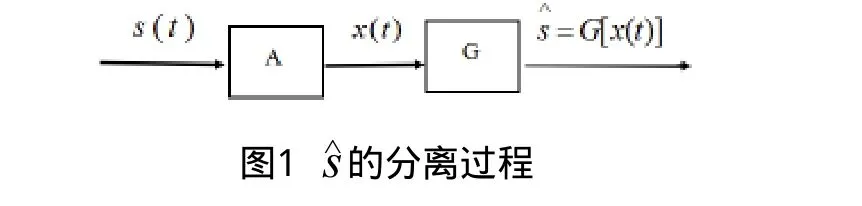
3 基于EMD-ICA信号处理思想

根据以上分析得出，EMD信号处理方法不受傅里叶分析限制，在信号的局部化领域进行EMD特殊的自适应时频分解，可以完成信号时频域图形的绘制，是一个比较有效的时频分析算法，适应于非平稳信号分析处理。ICA信号处理具有对信号通道和虚拟噪声通道进行多维度分析处理的能力，具备明显优势，但其存在检测信号数目必须大于等于源信号数目的局限性，通过少量的采集通道，往往难以达到特征信息准确分析的效果。为了弥补各自的缺陷，发挥他们各自的优势。提出了EMD-ICA联合信号处理步骤如下：

1）利用经验模式分解对监测信号进行分解，得到本征模分量（IMFS）；

2）然后对本征模分量利用相关性法则进行分析，利用较大相关性系数的分量函数构造虚拟的噪声通道；

3）利用Fast ICA对信号通道和虚拟噪声通道进行分析处理，实现各分量信号的分离，并进行后续的分析。过程如图2所示。

图2 信号分离过程

4 数据仿真分析

本文首先利用数据仿真来验证此方法的有效性。构建三个基本的正弦信号作为源信号的基信号，混合信号是随机产生的，并且为3×3矩阵，通过混合矩阵与基信号的作用产生混合信号，EMD无法完全分解这三个混合信号，结合EMDICA方法的应用，恢复分解得到的IMF分量所丢失信号，让其与基信号一个一个的比较，从而验证此种方法的有效性。

在仿真阶段设计的三个正弦基信号是比较简单的信号，其参数分别为：频率10Hz，20Hz，50Hz，相位差值为0，与频率对应的信号幅值分别为1mm，2mm，0.5mm。时域和频域波形图如图3～图5所示。

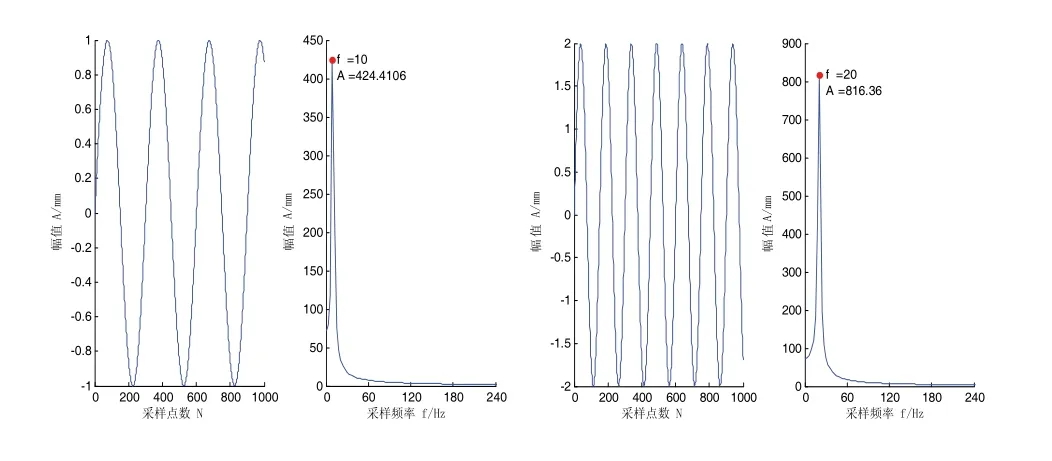
图3 频率10 Hz 图4 频率20 Hz

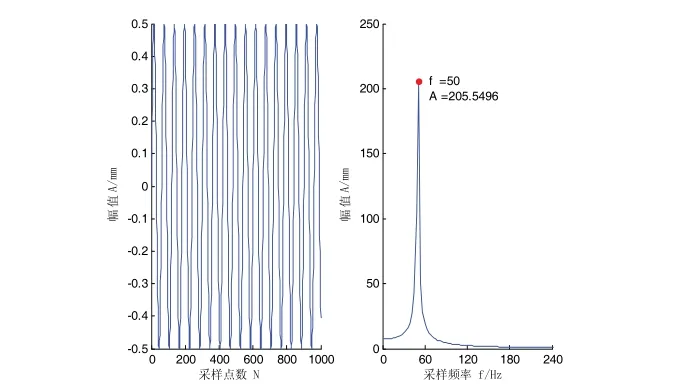
图5 频率50 Hz

经过矩阵作用后，其混合信号时域和频域波形如图6、图7所示。

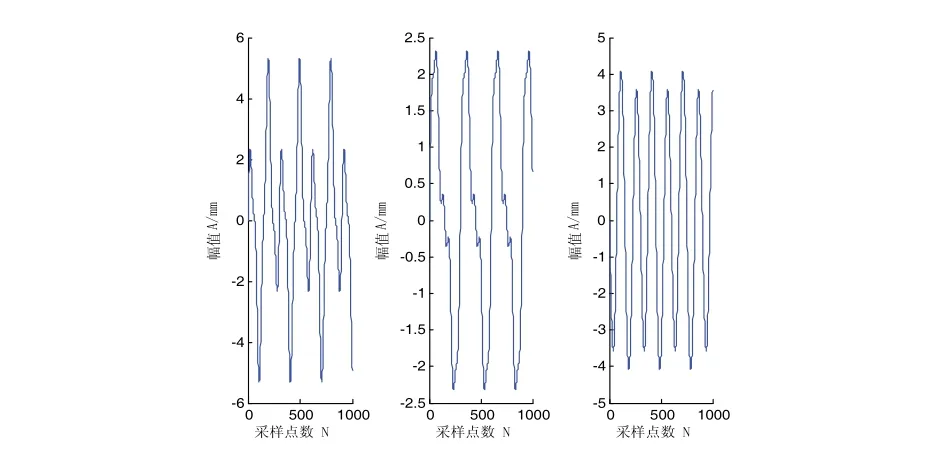
图6 混合后时域图

图7 混合后频域图

对混合信号按照EMD分解后处理，得出的IMF分量结果如图8～图10所示。

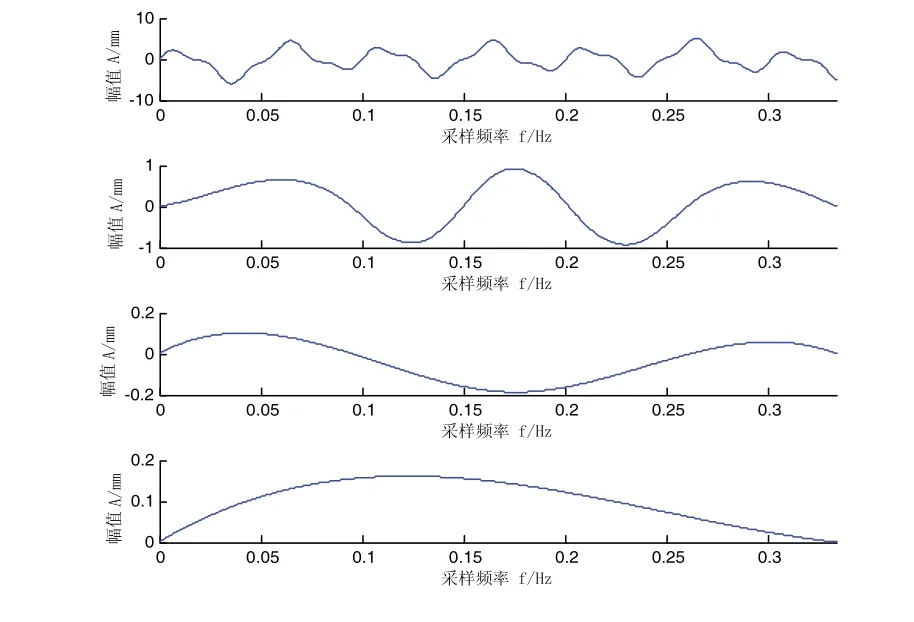
图8 混合信号1

图9 混合信号2

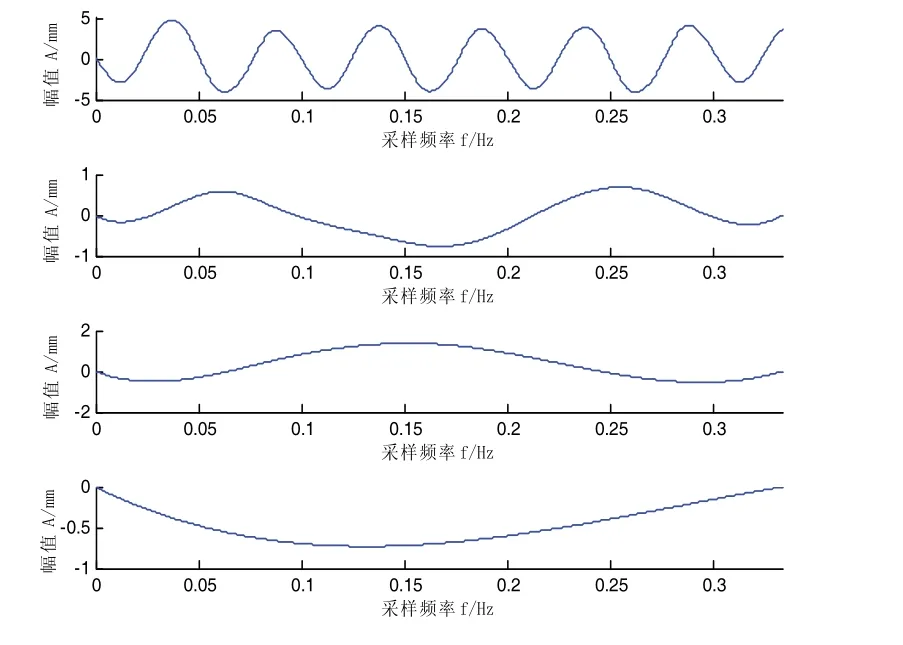
图10 混合信号3

从图中可以看出，虽然EMD对混合信号有一定的分解能力，这三幅图的第一个图均能表现出原来某个基信号的一些基本特征，但是其它的两个基信号都没有表现出来。下面经过相关系数处理，分别获得每个混合信号的IMF分量与各自混合信号的相互关系。如表1所示，为三个信号各IMF分量与各自混合信号的相关系数。

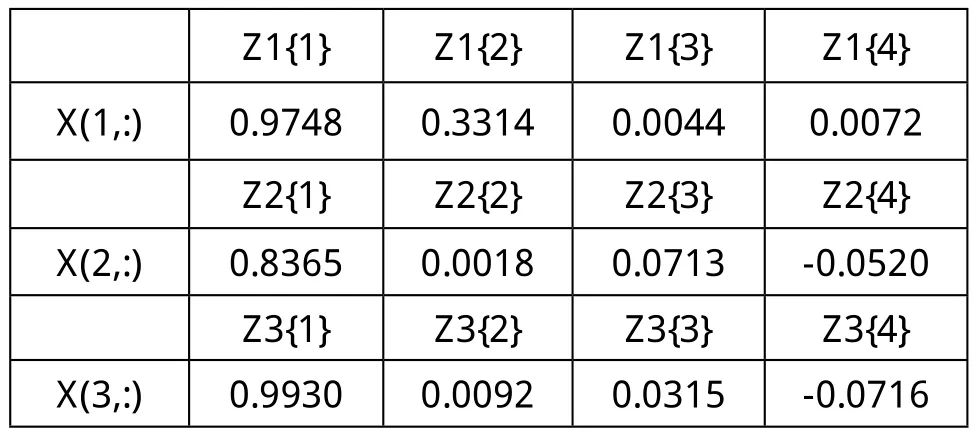
表1 仿真数据相关系数

将其中相关系数较大的几个分量进行求和处理，与各自混合信号一起作为ICA输入矩阵，进行Fast ICA处理，得到图谱如图11～图13所示。

图11 频率10 Hz

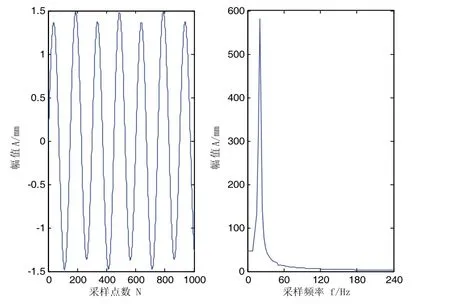
图12 频率20 Hz

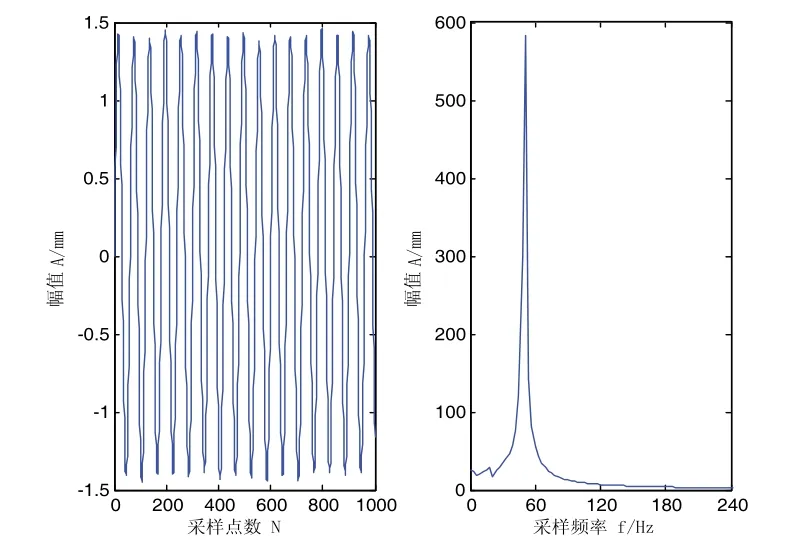
图13 频率50 Hz

从以上图中可以明显看出：经过EMD-ICA分解后，这三个图谱与基信号图谱基本一致，恢复了经EMD分解后所丢失的特征信息，还原了各信号的固有特征。

5 实验验证

下面再利用故障转子实验台来模拟机械设备旋转产生故障，对设备正常运行和碰摩故障信号进行分析。轴承型号为NSK6025ZZ，实验时故障转子运行转速为1750r/min，采样频率为12KHz，采样点数为2048。轴承的通常状态包括内圈故障、外圈故障、滚动体故障和正常，根据已有公式计算轴承每个部分的故障频率。外圈故障频率，内圈故障频率，滚动体故障频率分别为104.57Hz、157.94Hz、137.48Hz。实验得到时域波形数据如图14所示。

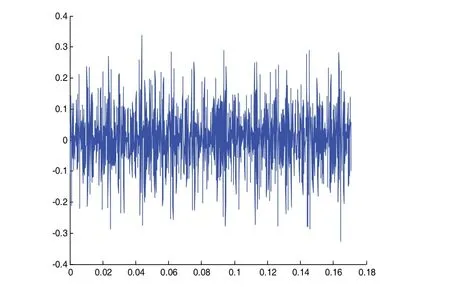
图14 时域图

经EMD分解后得到的各个IMF分量如图15所示。

图15 IMF图

相关系数如表2所示。

表2 实验数据相关系数

经过Fast ICA计算，结果如图16所示。

图16 时域和频域图

根据计算，得出故障特征频率fs = 157.2Hz，准确反应出了模拟的轴承内圈故障实验。

6 结束语

通过数据仿真以及实验台实验分析，采用EMD与ICA相结合的特征信号提取方法可以分离出各个IMF分量本身所固有的特性，消除EMD分解过后IMF之间的信息混叠现象，在一定程度上克服了盲目取舍本征模式函数而造成的信息成分丢失的缺点，同时解决了ICA输入源个数限制的要求，能够较理想的实现旋转设备振动信号的故障特征提取。该方法具有有效性。

[1] 丁康,陈健林,苏向荣. 平稳和非平稳振动信号的若干处理方法及发展[J].振动工程学报,2003,01:5-14.

[2] 李舜酩,郭海东,李殿荣.振动信号处理方法综述[J].仪器仪表学报,2013,08:1907-1915.

[3] Donoho D L,Johnstone I M.Adapting to Unknown Smoothness via Wavelet Shrinkage[J].Journal of the American Statiscal Association,1995,90(432):1200-1224.

[4] Donoho D L.De-Noising by Soft-Thresholding[J]. IEEE Transactions on information Theory.1995.41(3):613-627.

[5] 杨世锡,胡劲松,吴昭同,严拱标.旋转机械振动信号基于EMD的希尔伯特变换和小波变换时频分析比较[J].中国电机工程学报,2003,06:102-107.

[6] 周晓峰,杨世锡,甘春标.一种旋转机械振动信号的盲源分离消噪方法[J].振动.测试与诊断,2012,05:714-717,858-859.

[7] 季忠,金涛,杨炯明,秦树人.基于独立分量分析的消噪方法在旋转机械特征提取中的应用[J].中国机械工程,2005,01:52-55.

[8] Huang N E,Shen Z.The empirical mode decompos ition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences,1998, 454:903-995.

[9] 焦卫东,杨世锡,吴昭同.基于独立分量分析的噪声消除技术研究[J]. 浙江大学学报,2004,07:79-83,137.

[10]褚福磊,彭志科,冯志鹏,等.机械故障诊断中的现代信号处理方法[M].科学出版社,2009:109-125,173-243.