基于参数自适应EKF的隧道周边位移预测

凌同华，吴联迎，刘浩然，曹 峰，张 胜，李 洁

在新奥法施工中，隧道周边位移为隧道监控量测的必测项目［1］。对周边位移进行准确、及时的监测，同时据此进行可靠性的预测，以了解未来位移的变化发展趋势，为隧道稳定性控制和安全施工提供了动态参考。

由于隧道周边位移受多种因素的影响，而有些因素的影响难以进行定量和定性分析，使得周边位移具有非线性特性，因此，一般的数学方法难以恰当地对其进行描述和预测。目前，用于监控量测预测的方法很多，如：支持向量机［2］、灰色模型［3］、人工神经网络［4］、自适应模糊推理系统［5］及遗传算法［6］等，这些方法各有优劣。

卡尔曼滤波是当前应用最广的一种动态数据处理方法，具有最小无偏方差特性［7－10］。其滤波过程实质为一种递推算法，对所需估计的动态过程进行了线性估计。对于隧道周边位移这样的非线性过程，扩展卡尔曼滤波通过对其进行线性泰勒处理，使其得以实现滤波，该方法简单、有效。因此，扩展卡尔曼滤波为隧道周边位移预测提供了可靠的理论基础。在使用滤波算法时，需要精确的模型参数和噪声方差统计，否则，易致滤波发散，使得实际应用中存在一定的障碍。据此人们提出各式各样的自适应方法，以减弱模型误差和噪声方差统计不足的影响。在这些自适应方法中，人们更多地探讨了方差自适应方法，而未予讨论参数自适应法。作者拟采用参数自适应扩展卡尔曼滤波，对周边位移进行滤波预测处理，并探讨其适用性。

1 扩展卡尔曼滤波算法

1.1 卡尔曼滤波

对于线性随机系统，有

式中：xk，xk＋1分别为k，k＋1时刻系统状态向量；Ak为状态转移矩阵；Γk为系数矩阵；vk为观测向量，Ck为观测矩阵；ξk为系统噪声序列；ηk为观测噪声序列。

系统噪声序列和观测噪声序列相互独立，时变 噪 声 统 计 为：E （ξkξlT）＝Qkδkl，E （ηkηlT）＝Rkδkl，E（ξkηlT）＝0，E（ξkx0T）＝0，E（ηkx0T）＝0，其中：δkl为克罗蒂亚系数（k＝l时，δkl＝1；其余情形，δkl＝0）。卡尔曼滤波算法［11］可描述为：

式中：p0，0为初始误差估计矩阵；pk，k－1为一步预测误差矩阵；Gk为滤波增益矩阵；pk，k为估计误差矩阵；I 为单 位矩阵；x0，0为状态 估 计 初 始 值，x＾k，k－1为一步预测值，x＾k，k为状态估计值，Qk为过程噪声误差矩阵；Rk为观测噪声误差矩阵。

1.2 扩展卡尔曼滤波

对于非线性系统，有

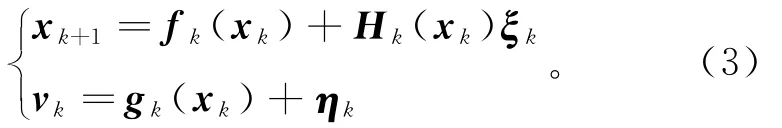
式中：fk为系统k至k＋1时刻的转移矩阵；Hk∈Rn×q为矩阵函数；gk为k时刻系统观测矩阵。

对于每个k，fk（xk）和gk（xk）对xk所有分量的一阶偏导都是连续的。以卡尔曼滤波算法为基础，进行泰勒线性处理，可得扩展卡尔曼滤波算法［11］。

2 参数自适应扩展卡尔曼滤波算法

扩展卡尔曼滤波的正常应用需要精确已知的模型参数和噪声方差统计，实际应用中往往难以得知，因此需要采取恰当的自适应方法进行弥补。目前较多的自适应方法集中于方差自适应方法，即通过方差的调整达到减小或增大增益Gk，从而实现一定程度的发散抑制。然而，滤波的发散受模型参数和噪声方差统计的双重影响。当模型参数已不适用于滤波计算时，方差自适应法也就约束不了滤波的发散了。因此，进行相关参数自适应方法的研究，弥补其在隧道变形预测分析应用中的空白，具有一定的意义。

2.1 残差特性因子

欲对滤波模型参数进行实时的修正，首先需判断模型的敛散趋势，可通过当前滤波预测残差绝对值与往期预测残差绝对值的均值的比值来加以判断，残差特性因子θ的定义表达式为：

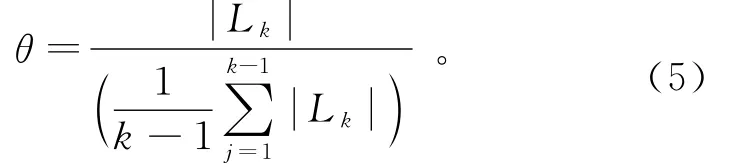
式中：Lk为预测残差，Lk＝vk－gk（x＾k，k－1）。

①当θ≤1时，即当前预测残差绝对值小于往期预测残差绝对值的均值，滤波正常。②当θ＞1时，即当前预测残差绝对值大于往期预测残差绝对值的均值，滤波出现偏离，可能发散，为预防滤波失效，可为θ设立阈值θ0（θ0可根据预测精度要求设立，如：取θ0为2或3）；当θ＞θ0时，判断为滤波发散。

2.2 模型参数调节系数

对扩展卡尔曼滤波进行一步预测，有

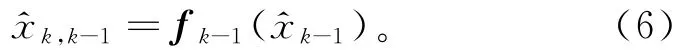
一步预测误差矩阵计算式为：

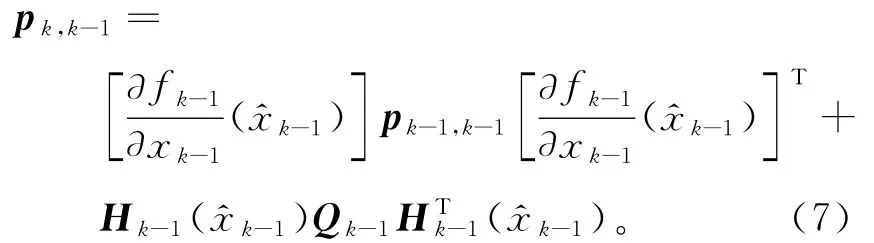
受模型参数的影响，需引入模型参数调节系数s（θ≤1时，滤波正常，取s＝1；θ＞1且θ＞θ0时，滤波发散，取s＝1＋α，α＝， 为经验参β数，可取为0.7～1.0）。根据残差特性因子，判断滤波的敛散性。利用模型参数调节系数，对滤波模型进行相应的缩放调节。进而抑制滤波发散，实现扩展卡尔曼滤波的参数自适应，则有

故对于k＝1，2，…，参数自适应扩展卡尔曼滤波算法可归结为：

3 工程实例分析

3.1 工程概况

葵坝路一标2号隧道，桩号YK3＋565～YK3＋600段洞顶埋深275～290m，净宽10.72m，内净高7.14m，岩质坚硬，解理裂隙不发育，围岩的完整性及稳定性均较好，自稳能力较强，设计围岩等级为Ⅱ级，采用新奥法原理进行设计与施工，全断面开挖。以YK3＋590断面周边位移为例，进行理论验证，测线布置如图1所示。（文献［1］中说明：一般地段全断面开挖时，布置一条水平测线即满足要求）

图1 断面测线布置Fig.1 Measuring line layout chart of section

3.2 实例分析

由于无法得知确切的周边收敛变化的转移方程，因此，采用前6期观测值进行曲线拟合，作为其转移方程，即：f（xk）＝5.398 5×exp（0.063 9xk），初始值可根据具体情况人为设置［12］，取p0，0＝0.025，Q0＝0.01，R0＝0.01，x＾0＝16.59。 依据标准型和参数自适应型扩展卡尔曼滤波算法，分别进行滤波预测处理，将两种滤波计算结果进行整理，见表1。

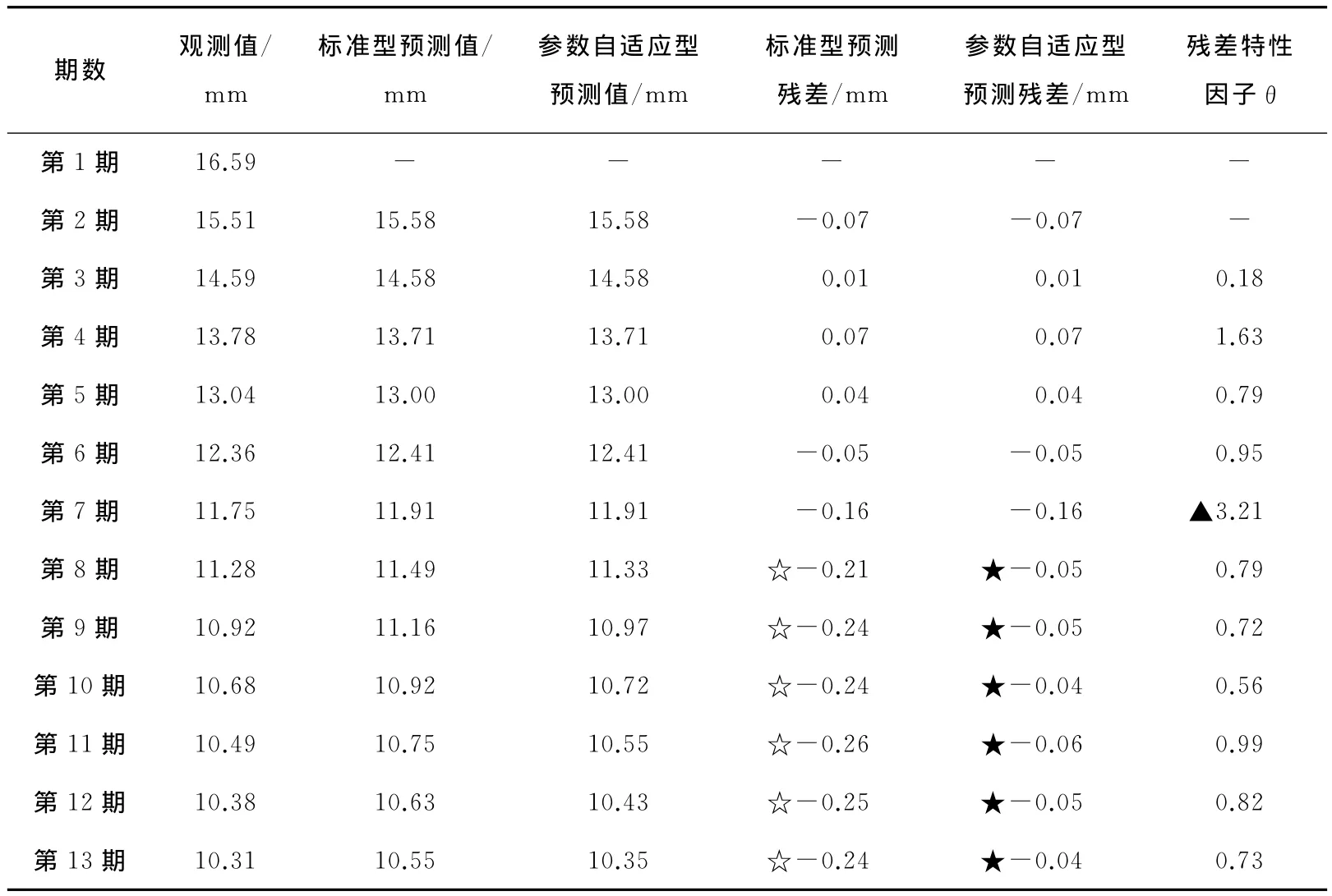
表1 标准型和参数自适应型扩展卡尔滤波计算的结果Table 1 Standard EKF and parameter adaptive EKF calculation

表1第7期中滤波预测的残差特性因子θ＝3.21大于预设的阈值（θ0＝2），滤波有发散的趋势，采用模型参数调节系数s进行修正。从表1中可以看出，修正后的参数自适应型预测残差（表1中标★处，其最大预测误差为0.06mm，平均预测误差为0.048mm）要明显小于未经修正的标准型预测残差（表1中标☆处，其最大预测误差为0.26mm，平均预测误差为0.24mm）。这说明参数自适应扩展卡尔曼滤波模型的预测值与观测值更为接近，其预测性能更优。

4 结论

1）参数自适应扩展卡尔曼滤波能有效抑制滤波发散，其预测值更接近于观测值，其预测效果优于标准型的。

2）用参数自适应扩展卡尔曼滤波模型进行隧道周边位移预测是可靠和精确的。通过该模型得知该断面AB预测平均误差为0.048mm，其最大误差为0.06mm，滤波预测精度较高，为隧道周边位移预测提供了一种新的方法。

（

）：

［1］ 吴从师，阳军生.隧道施工监控量测与超前地质预报［M］.北京：人民交通出版社，2012.（WU Cong－shi，YANG Jun－sheng.Construction monitoring and advance geological forecast in tunnel［M］.Beijing：China Communications Press，2012.（in Chinese））

［2］ 赵洪波.支持向量机在隧道围岩变形预测中的应用［J］.岩石力学与工程学报，2005，24（4）：649－652.（ZHAO Hong－bo.Predicting the surrounding deformations of tunnel using support vectormachine［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（4）：649－652.（in Chinese））

［3］ 徐昌茂，吴立，吴双兰，等.超大断面高速铁路隧道围岩变形预测分析［J］.现代隧道技术，2013，50（6）：80－84.（XU Chang－mao，WU Li，WU Shuang－lan，et al.Rock deformation prediction and analysis in highspeed railway tunnel with larger sections［J］.Modern Tunneling Technology，2013，50（6）：80－84.（in Chinese））

［4］ 王辉，陈剑平，邱道宏，等.洞室围岩压力预测的研究［J］.地下空间与工程学报，2009，5（2）：272－276.（WANG Hui，CHEN Jian－ping，QIU Dao－hong，et al.Study of prediction in surrounding rock pressure［J］.Chinese Journal of Underground Space and Engineering，2009，5（2）：272－276.（in Chinese））

［5］ 凌同华，易志强.基于自适应模糊推理系统的隧道周边位移预测［J］.中外公路，2011，31（1）：174－177.（LING Tong－hua，YI Zhi－qiang.Tunnel peripheral displacement prediction applying adaptive neuralfuzzy inference system［J］.Journal of China ＆ Foreign Highway，2011，31（1）：174－177.（in Chinese））

［6］ 马家超，朱珍德，朱姝，等.基于小波分析以及ESVR的隧道围岩位移时序预测［J］.水利与建筑工程学报，2013，11（2）：90－94.（MA Jia－chao，ZHU Zhen－de，ZHU Shu，et al.Prediction for tunnel surrounding rocks displacement time series based on wavelet analysis and E－SVR［J］.Journal of Water Resources and Architectural Engineering，2013，11（2）：90－94.（in Chinese））

［7］ 郑智忠，李亮，杨财，等.基于扩展卡尔曼滤波的汽车质心侧向速度观测器［J］.农业机械学报，2008，39（5）：1－9.（ZHENG Zhi－zhong，LI Liang，YANG Cai，et al.Vehicle lateral velocity observer using extended Kalman filter［J］.Transactions of the Chinese Society for Agricultural Machinery，2008，39（5）：1－9.（in Chinese））

［8］ 周伟静，沈怀荣.抗时值抑制发散滤波算法在无人机测风数据处理中的应用［J］.装备指挥技术学院学报，2009，20（5）：122－126.（ZHOU Wei－jing，SHEN Huai－rong.Filter algorithm with restraining outliers and divergence and its application in wind measurement data process with UAV［J］.Journal of the Academy of Equipment Command ＆ Technology，2009，20（5）：122－126.（in Chinese））

［9］ 刘伟，赵伟，刘建业.抗时值自适应Kalman滤波在无人机测风数据处理中的应用［J］.弹箭与制导学报，2011，31（3）：237－240.（LIU Wei，ZHAO Wei，LIU Jian－ye.Adaptive Kalman filter with restraining outliers in wind measurement data process with UAV［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2011，31（3）：237－240.（in Chinese））

［10］ 赵攀，戴义平，夏俊荣，等.卡尔曼滤波修正的风电场短期功率预测模型［J］.西安交通大学学报，2011，45（5）：47－51.（ZHAO Pan，DAI Yi－ping，XIA Junrong，et al.A Kalman filter based correction model for short－term wind power prediction［J］.Journal of Xi’an Jiaotong University，2011，45（5）：47－51.（in Chinese））

［11］ Chui C K，Guanrong C.卡尔曼滤波及其实时应用（第4版）［M］.北京：清华大学出版社，2013.（Chui C K，Guanrong C.Kalman filtering with real－time applications（fourth edition）［M］.Beijing：Tsinghua University Press，2013.（in Chinese））

［12］ 赵建三，胡启亮，唐利民，等.基于简化Sage－Husa自适应滤波算法的桥梁施工预拱度分析［J］.工程勘察，2012（11）：64－67.（ZHAO Jian－san，HU Qi－liang，TANG Li－min，et al.Application of simplified Sage－Husa adaptive filtering algorithm in bridge construction pte－camber analysis［J］.Geotechnical Investigation ＆ Surveying，2012（11）：64－67.（in Chinese））