基于MATLAB PDE的变压器二维建模和漏磁场分析

晋建厂, 王伟



基于MATLAB PDE的变压器二维建模和漏磁场分析

晋建厂1, 王伟2

（1. 海军装备部，北京 100841；2. 中国舰船研究设计中心，武汉 430064）

MATLAB提供了一个偏微分方程求解的工具箱（PDE），利用该工具可以实现偏微分方程类型的设定、几何模型建立、方程求解和结果图形化显示。变压器短路阻抗主要由漏磁场决定，本文通过建立变压器的二维模型，并利用MATLAB PDE工具箱进行分析计算漏磁场，并在此基础上采用能量法计算了变压器漏磁通和短路阻抗大小，得到了短路阻抗与变压器结构的关系。

变压器 短路阻抗 MATLAB PDE

0 前言

船舶电力推进系统一般由变压器、变频器及推进电机组成。变压器的短路阻抗是变压器的重要参数之一，该参数过大则压降较大，影响输出电压；该参数过小则导致短路电流过大，不利于系统保护。变压器短路阻抗主要由漏磁场决定，本文通过建立变压器的二维模型，并利用MATLAB PDE工具箱进行分析计算漏磁场，得到了短路阻抗与变压器结构的关系。

1 变压器漏磁场分析及其二维模型

变压器中其和等于零的磁势所建立的磁场叫做变压器的漏磁场，本节以双绕组变压器为例。变压器的磁场可以看做是由两个部分组成，其一是励磁磁势建立主磁通，其二是由磁势和为零的二次电流和一次电流负载分量建立的磁场成为漏磁场，按照全电流定律，漏磁磁势不可能产生与变压器两个线圈都交链的磁通，仅可能包含与一个线圈逐次或者完全交链的磁通。经过上述分析，可以知道漏磁通只交链一个线圈，考虑到绕组绕在芯柱上呈圆形，故认为漏磁场是一个轴对称场，即沿着轴向对称轴不同的位置(角度)漏磁场近似相等，这样就给简化漏磁场的分析带来了条件，即可以把三维的漏磁场简化为二维的情况分析，但是二维的简化也是有选择性的，由于芯柱是连接铁轭构成了铁心窗口，所以有考虑或者不计铁芯窗口对漏磁场影响两种简化方式。为了分析的方便，本文在简化过程中，不计铁芯的磁滞效应, 忽略铁芯的饱和, 各向异性, 近似认为铁芯磁导率为无穷大;且忽略变压器绕组的各种支架、铁芯拉板、夹件等对漏磁场的影响。下面对两种简化的模型进行介绍。

考虑铁芯窗口对漏磁的影响，这样在简化过程中要把铁轭表现出来，如图1，图中R1为变压器芯柱二维模型，R4、R5为铁芯窗口，R3、R6为变压器A相低压绕组，R2、R7为变压器A相高压绕组；B、C相与A相相同；R16为油箱。

2 MATLAB PDE工具箱介绍

MATLAB提供了一个偏微分方程求解的工具箱（PDE），利用该工具可以实现偏微分方程类型的设定、几何模型建立、参数给定、边界条件的设定、三角网格的划分和细化以及方程求解和结果图形化显示，这是标准的有限元方法计算的流程。磁场分析的基础是麦克斯韦方程组，麦克斯韦方程组有积分和微分两种形式，针对于MATLAB PDE工具箱是一个偏微分方程的求解工具，本文主要讨论了麦克斯韦方程的微分形式以及在PDE中应用。经过分析，在求解过程中以不同物理量建立的方程其形式和求解的难易程度不同。以场量磁感应强度和磁场强度为直接待求量的微分方程如下：

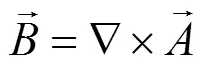
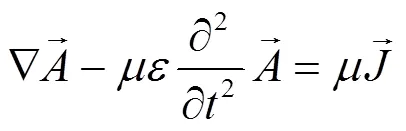
观察方程（4），矢量磁位在x,y,z三个方向都有自由度，这样分析较为麻烦，针对于变压器漏磁场的结构特点，前文提出的变压器的二维漏磁场分析模型，将矢量磁位的自由度由x,y,z三个方向上减少到z轴方向上。MATLAB PDE工具箱提供了两种求解模式，一种是利用图形用户界面（GUI）求解，另一种是利用函数命令行的方法求解。利用GUI可以直观、快速、准确的实现偏微分方程的求解，本文主要介绍应用GUI求解模式进行变压器磁场分析。PDE工具箱一共能够解四种形式的偏微分方程（组），本文选择双曲线PDE方程：

前文已经把求解域简化为二维的情况，所以矢量磁位方程可以化为标量方程，矢量磁位只有在z轴上有分量，即：

将变压器的物理特性参数与方程的系数对应起来即可求解。本文选用的模型中，一般认为磁力线不超出变压器油箱，磁力线又是磁位AZ的等势线，所以这里设置其边界条件为齐次Dirichlet条件，设置AZ在边界上全部为零，在边界上建立一个封闭的磁力线，由于磁力线不能交叉，所以这样就能把求解域里的磁力线约束在油箱里面。

3 仿真结果的后处理方法

在MATLAB PDE中能够直接输出的是网格节点上的矢量磁位值（离散解），矢量磁位Az并不是最终要求解的物理量，对于磁场分析，最基本的是要求出场域上的磁感应强度B的值，对于只有z轴分量的矢量磁位AZ来说，两者之间的关系如下。

从上式中可以看出，需要求出矢量磁位Az在场域上的连续解，本文采用一阶线性插值的方法，通过直接输出的离散解求出矢量磁位的连续解，进而求出场域上磁感应强度的分布。求解出磁感应强度的分布后，就可以进行进一步的计算，本文主要计算了变压器的短路阻抗，运用能量法计算短路阻抗，下面介绍一下其原理。对于磁场的储能从不同的角度分析可以推导出不同的表达式，漏磁场的储能公式可以表示为：

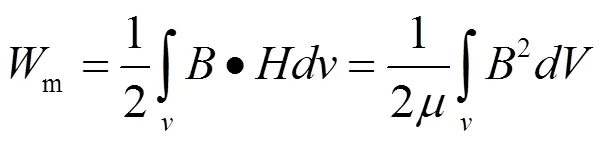
上式中:V为漏磁通分布三维区域。

由于变压器的漏磁场已经简化为二维场来进行求解的，且经过分析，变压器的漏磁场是轴对称的，即能量的求解区域为旋转体，所以上式进行如下简化：

考虑到有限元离散化，上式可以简化为：

式（11）对应于单相（或室磁场为静态场）情况下，对于三相交变磁场则有：

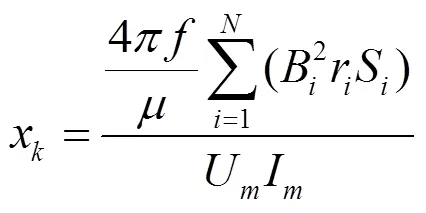
上式中：U为变压器额定相电压（这个在计算时需要根据绕组的连接方式确定）。至此已经分析了变压器漏磁场简化为二维的原理、PDE工具箱应用模式的选择、求解计算的原理以及关键参数的设置和数据的后处理方法，便可进行仿真计算和结果分析。

4 仿真结果分析

从上面的分析中可以看到，静磁学下的椭圆形方程相对简单，对于变压器工频交流磁场，属于低频问题，把它简化为静磁场求解是比较简单的，实际仿真过程中也大大缩短了仿真时间，本文以变压器STQK-1600/10为例建立模型进行仿真。变压器在额定工作状态下，其铁芯工作在线性区，上面分析出漏磁通之交链于一个线圈，故认为三相之间的漏磁场分布独立，下图是应用静磁场椭圆形方程，故对B相绕组施加直流激励所得到的仿真结果图。

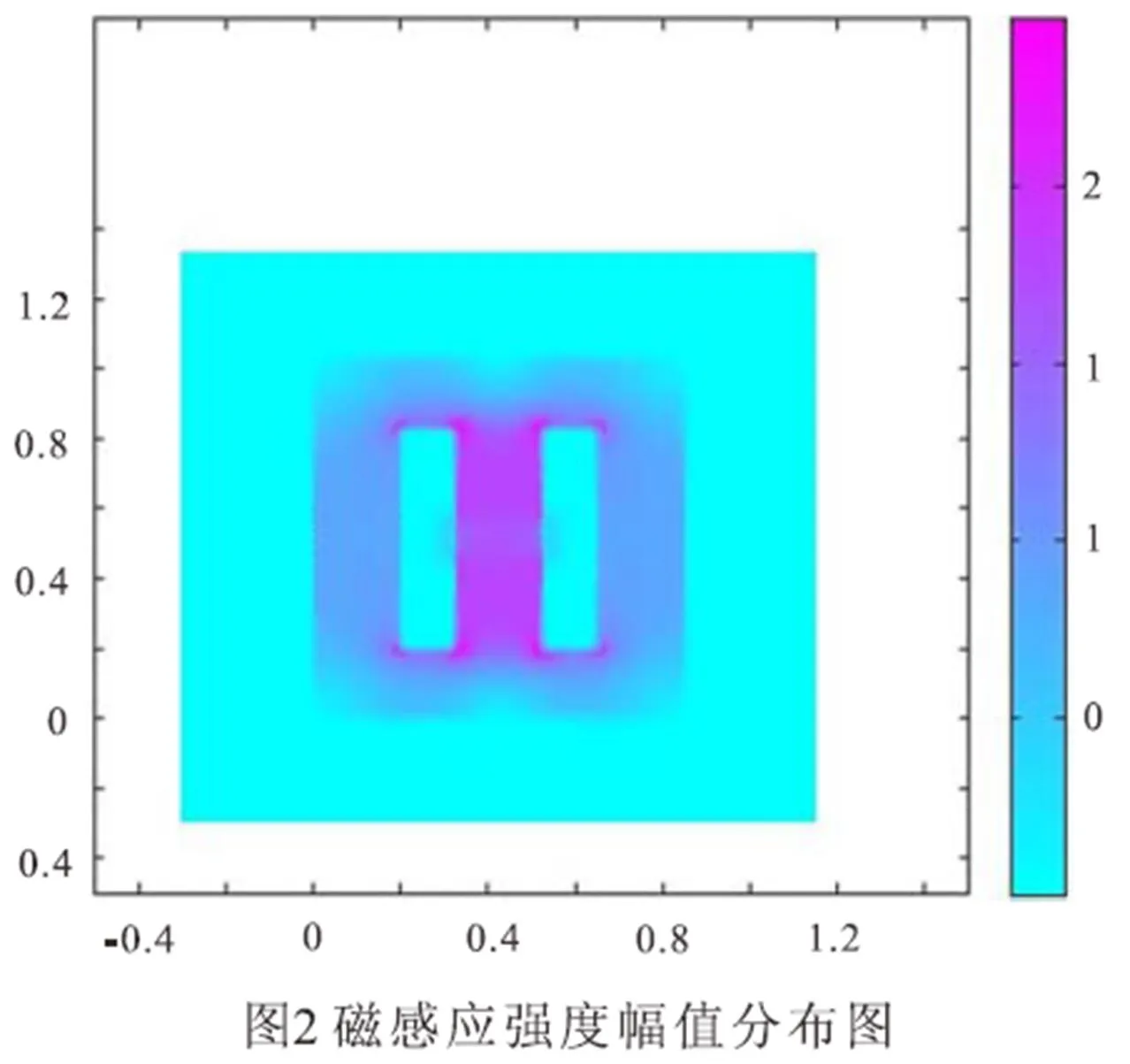
从图2中可以一看出，磁通主要分布在铁芯中，漏磁通占很小的部分，下面具体分析变压器漏磁场的分布特点。图3、图4为高压绕组轴向中心线上磁感应强度轴向分量分布图。

从图4中可以看出，高压绕组中心线上磁感应强度辐向分量从下端到上端先变大、在1/4处开始变小，在1/2处反向变大，在3/4处又开始变小，并在末端反向，其分布规律在轴向具有对称性。本次仿真模型中，低压绕组高度约为高压绕组的一半，其中心在一个高度上，所以在中心点处磁势平衡，幅向磁感应强度为0，从中心往上和往下分析，由于在同一高度上的磁势不平衡变得越来越明显（低压绕组的磁势较大），幅向漏磁逐渐变大，到达1/4和3/4处时即大约低压绕组两端处，磁力线发散、漏磁磁阻变大，磁感应强度又开始变小，到达高压绕组端部时，由于此处高压绕组的磁势的影响大于低压绕组磁势的影响，磁感应强度开始反向，但由于端部磁力线发散、磁阻较大，磁感应强度幅值很小。

图5、图6分别为低压绕组轴向中心线上磁感应强度轴向和幅向分量分布图。

可以看出低压绕组轴向中心线上磁感应强度的分布于高压绕组遵循相同的规律，但低压绕组处的磁感应强度辐向分量要大于高压绕组同一位置，这说明由于同一高度上的磁势不平横对低压绕组的影响大于高压绕组。仿真有关结论如下：低压绕组与高压绕组之间的绝缘距离越短，磁阻越小，漏磁通越大，短路阻抗越大。高低压绕组高度不一样，会造成幅向漏磁通很大，可采用分层或者分段的方法尽量保证高低压绕组高度一致，以减少幅向漏磁通，进而减小短路阻抗。

[1] 吴小庆. 数学物理方程[M].成都：电子科技大学出版社，2004.

[2] 苏金明，阮沈勇，王永利. MATLAB工程数学[M].北京：电子工业出版社，2005.

[3] 陆君安. 偏微分方程的MATLAB解法[M]. 武汉：武汉大学出版社.

[4] 黄作英，阙沛文，陈亮. PDE工具箱实现偏微分方程的有限元求解. 计算机仿真, 2006, (23)9.

Analysis on Leakage Magnetic Field and Modeling for Transformer Based on MATLAB PDE

Jin Jianchang1,Wang Wei2

(1. Naval Equipment Department, Beijing 100841, china ; 2. China Ship Development and Design Center，Wuhan 430064，China)

2014-09-13

TM421

A

1003-4862（2014）11-0021-04

晋建厂(1982-), 男，本科。研究方向：船舶电力推进系统。