一种等高线内插的新方法

林春峰 闵世平 黄华平

(中铁二院工程集团有限责任公司，四川成都 610031)

1 概述

为了提高生产效率，在数字化制图中需要利用已知的等高线进行内插，目前常用方法有网格内插、三角网内插、辅助线内插等［1-7］。网格内插和三角网内插的计算量较大，在实际应用中，会显得较迟钝;辅助线内插方法计算速度快，但由于采用的数据点较少，数据点的分布位置不佳，在一些等高线急剧变化的地方，内插出的等高线存在较大失真［8］。结合辅助线方法的特点，提出一种新的内插方法，首先利用特征参数对已知的等高线节点进行描述;再利用特征参数进行等高线节点匹配，将等高线分割成不同的区域，分区域进行辅助线构建，利用构建的辅助线内插等高线;最后对内插出的等高线进行节点简化，得到最终结果。实验结果表明，利用该方法内插的等高线能够很好的顾及局部地形，有效地解决等高线内插的问题。

2 算法介绍

等高线内插要解决的问题可以转化成:在相邻两条已知等高线l1和l2中，内插N条等高线。其中，假定l1和l2节点排列顺序一致，N为已知常数。

算法首先按照给定的规则计算等高线l1和l2上每个节点的特征参数;然后利用匹配规则进行节点匹配，将l1和l2分割成一一对应的区域;然后对各个区域进行辅助线构建，利用构建后的辅助线内插等高线;最后进行节点简化，得到最终结果。

2.1 节点特征参数计算

节点特征参数的定义为

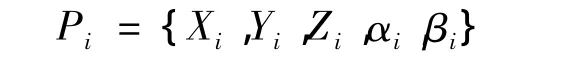
Pi为某条等高线上第i个节点的特征参数。其中:i∈［0，n］，n 为等高线节点的个数;Xi、Yi和 Zi为节点的坐标值;αi为前一节点和当前节点连线与水平方向夹角角度值，αi∈［0，360);βi为当前节点和后一节点连线与水平方向夹角角度值，βi∈［0，360)，如图1所示。

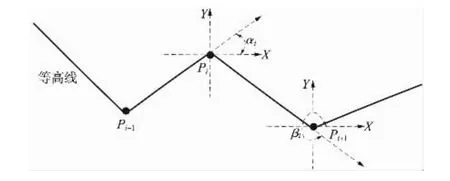
图1 角度参数计算示意

αi和βi的计算公式如下

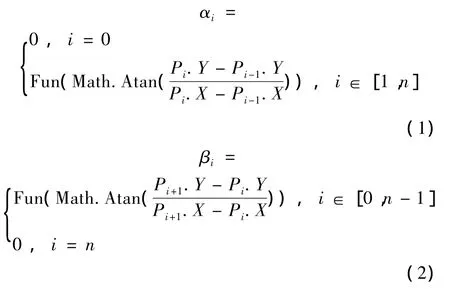
其中，函数Fun(Math．Atan(k))表示计算斜率为k的向量与水平轴正方向夹角，夹角数值大于0、小于360。

2.2 节点匹配

对已知两条等高线l1和l2所有节点，按照2.1小节对节点特征参数的定义以及公式(1)、(2)进行计算，得到等高线l1和l2所有节点的特征参数集合

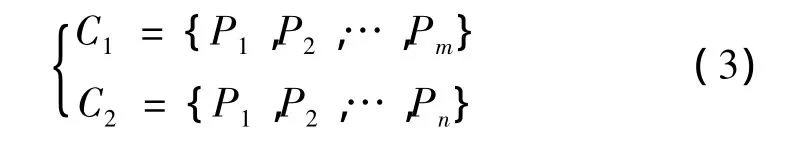
其中，m和n为等高线l1和l2节点个数。

以两条等高线中节点个数多的那条为基准，遍历该条等高线上的每一个节点，假设当前节点为Pc，然后在另外一条等高线中寻找距离该点最近的M个点集合R，计算点Pc与点集合R中每个点Pi(Pi∈R，i∈［0，M］)的特征距离 Di，计算公式为

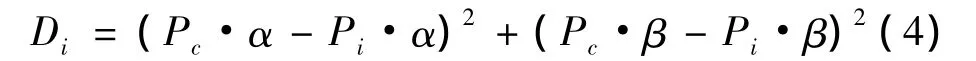
其中，Pi∈R，i∈［0，M］。

设定距离阈值d，当Di大于d时，进行下一点的判断;否则认为Pi是Pc的变化趋势一致点，记录Pc和Pi两点的坐标，这两点的连线即能将等高线分割成两部分。

对基准等高线上所有的节点匹配完成之后，就能得到一组匹配结果，将其图形化表示，如图2所示。

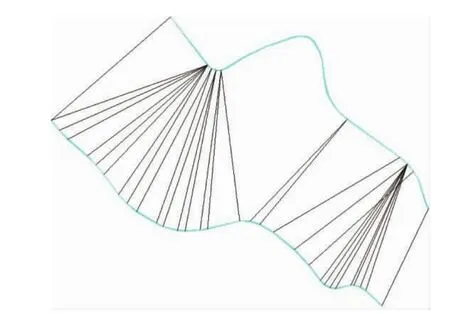
图2 节点特征匹配

节点特征匹配结果可以将两条等高线分割成多个匹配区域，但是通过图形化结果发现:匹配区域有交叉重叠部分和共点部分，需要按照一定的规则对匹配结果进行筛除，即剔除图2中相交和共点的线。筛除规则如下:

①依次遍历匹配结果集合，取出当前匹配结果，获得匹配结果中两点分别在两条等高线中节点的序号index11、index21;

②取出前一匹配结果，获得前一匹配结果中两点分别在两条等高线中节点的序号index10、index20;

③当index21＜=index20，则剔除该匹配结果;否则继续执行①、②、③，直到所有的匹配结果遍历完成，得到如图3所示的结果。

图3 特征匹配错误剔除

2.3 辅助线构造

相邻两组匹配结果可以将两条等高线分割成变化趋势一致的区域，依次遍历筛选后的匹配结果，取当前和下一组匹配结果，得到其分割两条已知等高线的区域，进行定数等分，然后依次匹配两条等高线上的定数等分点，存入辅助线数组。图形化的辅助线如图4所示。

2.4 等高线生成

假设每根辅助线的起止点坐标为(X1，Y1，Z1)和(X2，Y2，Z2)，可以得到待内插的N条等高线的节点坐标

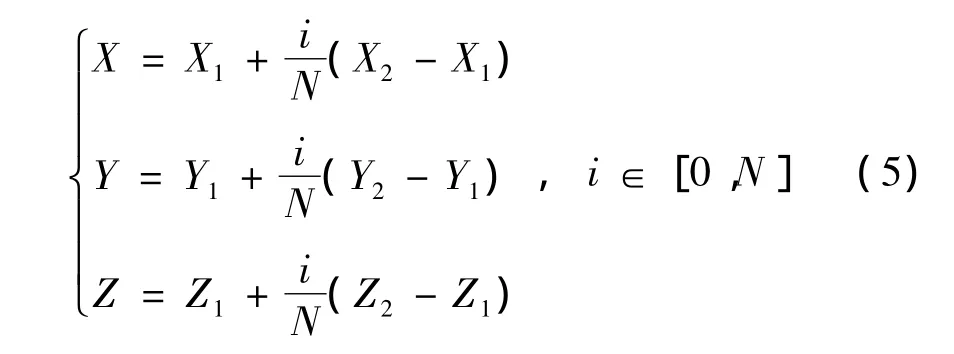
以此遍历每根辅助线，计算内插点坐标，将内差点连接起来，即可得到等高线，如图5所示。

图4 构造辅助线

图5 通过构造线内插等高线

上述方法会造成等高线线上节点过多，道格拉斯－普克算法能够准确的删除线段上小弯曲的节点，在整体上有效保持了线要素的形态特征［9］。因此，在得到等高线后，利用道格拉斯－普克算法进行简化，得到最终结果，如图6所示。

图6 道格拉斯－普克简化后的等高线

3 实验及分析

利用等高线上当前节点坐标值，以及当前节点和前后两个相邻节点向量与水平轴正方向的两个夹角数值当作描述当前节点的特征参数，一方面能够准确地确定节点的空间位置;同时，两个角度数值能够很好的确定当前节点在空间中的方位，便于在另一条等高线上寻找变化趋势一致点。寻找到了变化趋势一致点后，有利于将已知的等高线进行区域分割。同一分割区域内，两条已知等高线变化趋势是一致的。最后，在变化趋势已知的分割区域内，进行辅助线构造、等高线生成、节点简化等操作，得到最后的结果。

利用本文提出的新方法进行等高线的生成，并利用文献［4］提出的算法进行对比实验，对比结果如图7所示，其中中间部分实现为本算法内插结果，虚线为文献［4］提出算法的结果。

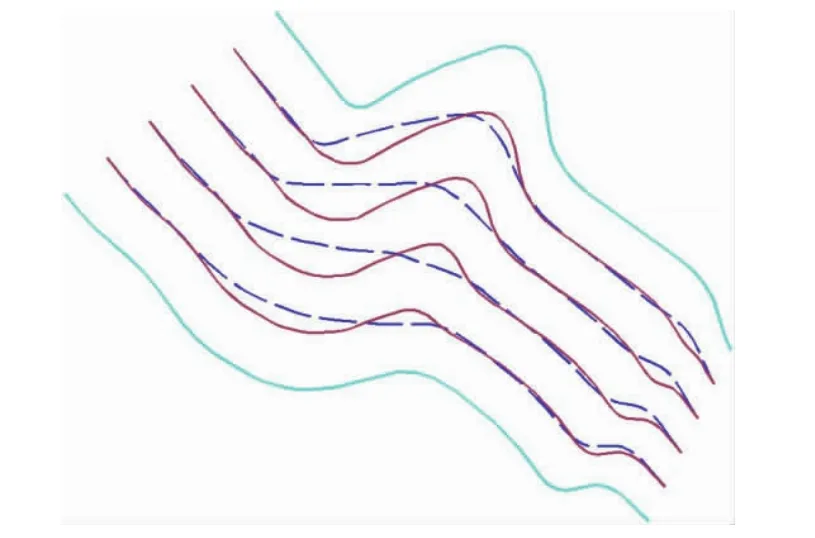
图7 内插等高线结果对比

经过对比分析可知，本文提出的新方法能够很好的顾及局部地形，可以更好地解决等高线内插的问题。

［1］ 龚有亮，何玉华，付子傲，等．一种实用的等高线内插算法［J］．测绘学院学报，2002，19(1):36-37

［2］ 胡卫明，吴兵，凌海滨．地图等高线内插算法［J］．计算机学报，2000，23(8):847-851

［3］ 杨长强，郑永果，郑作亚．一种等高线自动加密算法［J］．信息技术与信息化，2006(2):56-58

［4］ 李洪玉，唐诗华，李景文，等．在CAD中实现等高线自动内插的一种方法［J］．海洋测绘，2004，24(3):52-54

［5］ 张渭军，王文科，孔金玲，等．等雨量线的自动绘制方法［J］．水土保持通报，2006，25(5):54-57

［6］ 曹颖，赵牡丹．DLG内插等高线算法实现［J］．测绘科学，2007，32(2):67-68

［7］ 黄培之．等高线形状变化规律的研究［J］．中国图象图形学报，2006，11(1):103-106

［8］ 姜波．一种等高线内插的新思路［J］．科技通报，2010，26(5):780-781

［9］ 彭认灿，董箭，郑义东，等．垂距法与道格拉斯－普克法删除冗余顶点效率的比较［J］．测绘通报，2010(3):66-67