基于云模型和Theil指数的投资项目风险评估研究
汪新凡,吴兴奎
(1. 湖南工业大学 理学院,湖南 株洲 412007;2. 湖南工业大学 财经学院,湖南 株洲 412007)
基于云模型和Theil指数的投资项目风险评估研究
汪新凡1,吴兴奎2
(1. 湖南工业大学 理学院,湖南 株洲 412007;2. 湖南工业大学 财经学院,湖南 株洲 412007)
从企业家及团队风险、产品风险、技术风险、市场风险、退出风险、政策及产业风险和区域影响力7个方面构建了投资项目风险评估指标体系,进而基于云模型和Theil指数提出了一种风险评估方法。该方法先将指标值转化为云模型,然后利用云的特征数和Theil指数计算指标权重,再以此权重为基础进行云模型集结,从而对各方案进行综合评估和择优。最后,通过实例应用检验了该方法的可行性和有效性。
风险投资项目;风险评估;云模型;Theil指数
1 研究背景
所谓风险投资,是指投资人将资本投向刚创立或快速发展的未上市公司(主要是高科技公司),在承担巨大风险的基础上为融资人提供长期股权投资和增值服务,培育企业快速发展,多年后再通过上市、兼并或其他股权转让方式撤出投资,从而获得高额投资回报的投资方式[1]。风险投资与传统的项目投资相比,需要考虑很多不确定性因素。这些因素主要有:1)高新技术,风险投资的主要对象是高科技产业,其新技术处于当代科技的前沿,发展态势不明朗,新技术从原理构思到组织实施,都会由于各种原因造成许多不确定性;开发出来的技术能否转化为生产力,也存在不确定性。2)高投入,风险投资的方向是具有高成长性的未上市公司,从技术开发、成果转化到规模生产,各环节都需要大量资金投入。3)高风险,高新、创新企业是风险投资的重点,而这类企业可借鉴的成熟经验不多,同时由于人才、管理、技术、市场等诸多不确定环节又包含诸多不确定、不完善因素,造成风险投资具有很高的风险性。4)高收益,风险投资的项目一旦成功收益就很大,回报率非常高。因此,风险投资公司在选择投资项目时非常慎重,通常请专家对各项目进行风险评估,以尽可能降低风险,获取高额回报。
投资项目风险评估指标体系的构建是风险评估的基础,国外学者对此研究较早。20世纪70年代,W. A. Wells等人[2-3]经过大量调研,从管理、收益率等方面,总结出管理者素质、产品风险等12个评估指标。T. T. Tyebjee等人[4]在定性阐述评估准则的基础上,建立了包括产品吸引力、产品差异性等5类主要评估指标。之后,I. C. Macmillan等人[5]通过问卷调查,给出竞争风险、退出风险等6类评估指标。V. H. Fried等人[6]通过对风险投资家进行实地访谈,提出应从战略思想、管理能力和收益3个方面对风险企业进行评估。S. N. Kaplan等人[7]选取了10家风险投资机构,首次对项目评估与投资合同设计关系进行实证研究,总结出投资机遇、管理层、投资合同和外部投融资环境4类评估标准。M. Kakati[8]利用cluter因素和主因素分析法对高新技术风险投资中的投资标准进行探索,提出了企业家素质、资源获取、竞争策略、产品特征、产品市场和金融因素6个评估标准。
由于受国外学者影响,国内学者大多重视项目本身风险的论证和分析。成思危[9]从完善风险投资发展的需要,根据我国的国情,提出政策因素作为风险投资评估的一个重要依据,具有很强的现实意义。刘常勇等人[10]对我国台湾地区的风险投资活动进行实地调查,从经营计划书、经营机构等5个方面构建了22个指标的评估体系。汤京华等人[11]在对中外风险投资的发展现状作了研究之后,提出产品差异度、市场吸引力等5个方面14个指标的评估体系。王世波等人[1]对浙江省和其他一些省份的风险投资公司进行访谈和问卷调查,提出了基于创业者素质、技术、市场和管理4个方面共15个指标的评估体系。另外,周乃敏等人[12-14]从宏观环境角度出发,建立了包括政治稳定性、利率稳定性等4个方面的评估指标体系。张春英等人[15-16]建立了包括技术风险、研发风险、生产风险、市场风险、管理风险和财务风险6个方面的评估指标体系。
通过对比研究发现,国内外学者提出的投资项目风险评估指标体系存在一定的相似性,主要关注风险投资项目在产品、市场、技术、管理水平以及环境等方面的风险因素,但由于各国风险投资业发展成熟度不一致,在评估的具体指标上又存在差异。本文在相关研究的基础上,分析风险投资过程中潜在的风险因素,构建投资项目风险评估指标体系,且利用云模型[17]和Theil指数[18]提出一种投资项目风险评估方法,并进行实例分析。
2 构建投资项目风险评估指标体系
在国内外风险评估指标体系研究的基础上,根据我国的实际情况,本文从企业家及团队风险、产品风险、技术风险、市场风险、退出风险、政策及产业风险、区域影响力7个一级指标和34个二级指标构建风险投资项目的风险评估指标体系,如表1所示。

表1 投资项目风险评估指标体系Table1 Risk assessment index system of investment project
3 基于云模型和Theil指数的投资项目风险评估模型
3.1 问题描述
在第2章提出的投资项目风险评估指标体系中,7个一级评估指标用Bj=(j=1, 2, …, 7)表示。B1下的8个二级指标用C1~C8表示,B2下的5个二级指标用C9~C13表示,B3下的4个二级指标用C14~C17表示,B4下的6个二级指标用C18~C23表示,B5下的4个二级指标用C24~C27表示,B6下的3个二级指标用C28~ C30表示,B7下的4个二级指标用C31~C34表示。假设p位专家(专家权重向量为,其中)按10分制对n个备选投资项目进行评价,给出的每个二级指标Ck的评价值为区间数。令第l位专家给出的第i个投资项目关于第k 个二级指标的区间评价值为。设专家的权重向量已知,指标的权重向量未知,需要确定备选投资项目的排序,并选择最优方案。
3.2 利用云模型对专家给出的区间数据进行处理
云模型[17]由李德毅院士提出。云是用自然语言描述的某个定性概念与该概念的数值表示之间的不确定性转换模型,其中正态云模型[19]最为常用。正态云通常用3个数字特征进行刻画,分别称为期望Ex、熵En和超熵He。其中,期望Ex是定性概念在对应的数值论域中的中心值,熵En是定性概念模糊程度的度量,超熵He反映了云滴的离散程度以及隶属度的随机性变化。通常,一朵正态云用表示。
由于客观事物的不确定性,某些定性概念有时用区间数表达更符合实际。利用于少伟等人[20]提出的基于区间数据的逆向云发生器算法,可以将区间数转换为该定性概念的云模型。但该算法没有考虑区间数据本身的重要性权重。以下对该算法进行改进,并用于将专家给出的区间数据转化为云模型,具体算法如下:
1)针对p位专家给出的投资项目Xi关于第k个二级指标的区间评价值,把这些数据的下限和上限分别处理成数列的形式,得到区间数的下限数列和上限数列。
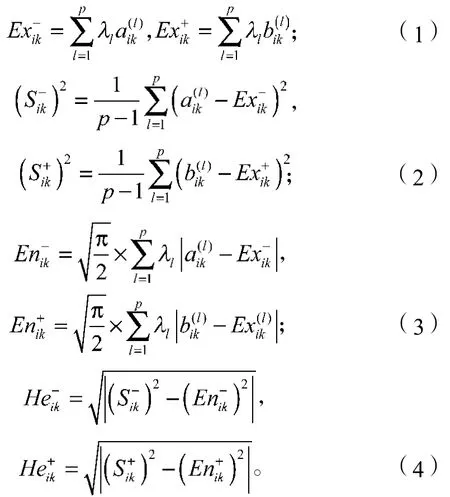
3)利用公式(5)~(7)计算,得到各二级指标的综合期望Exik、综合熵Enik和综合超熵Eeik,得到投资项目Xi关于第k个二级指标的综合云。
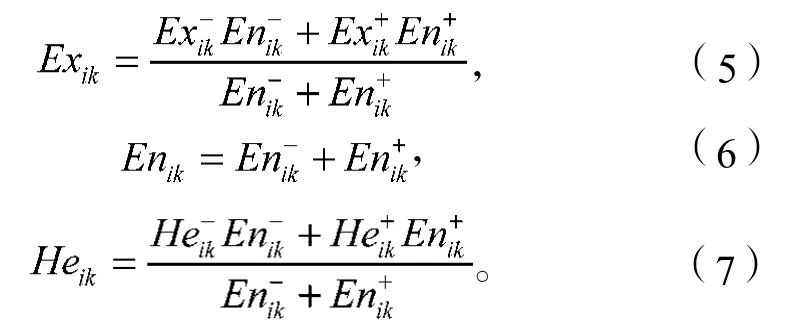
假设各一级指标Bj的云决策矩阵记为
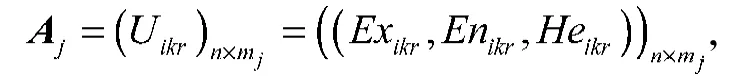
式中:j=1, 2,…, 7;i=1, 2,…, n;k=1, 2,…, 34;r=1, 2,…, mj,表示综合云在矩阵Aj中处在第r列,其中m1=8, m2=5, m3=4, m4=6, m5=4, m6=3, m7=4。
3.3 利用Theil指数确定二级指标的权重
Theil不均衡指数是由Henry Theil[18]最早提出,并用于衡量收入不平等程度的一个指标,被广泛应用于研究收入分配不平等和区域经济差距等问题。Theil不均衡指数的大小反映收入不均衡的大小,指数越大,表明不平等性越强,即收入差距越大。依照Theil不均衡指数的基本思想,在项目投资评估中,可以先运用Theil不均衡指数的计算方法,计算出评价指标的不均衡度,再利用评价指标的不均衡度计算出该指标的权重。评价指标的不均衡度反映不同项目指标值之间离散程度的大小,指标值之间的离散程度越大,说明该指标对综合评价结果的影响越大,应给予的权重越大。在极端情况下,若某项指标的值全部相等,则该指标在综合评价中将不起作用,可以剔除。下面根据投资项目Xi关于第k个二级指标的期望值Exik,利用Theil指数求取各二级指标的权重。
设一级指标Bj下的二级指标的期望值构成矩阵
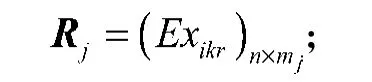
各二级指标Ck的权重为kr,其中kr≥0,。对决策矩阵,引入Theil不均衡指数
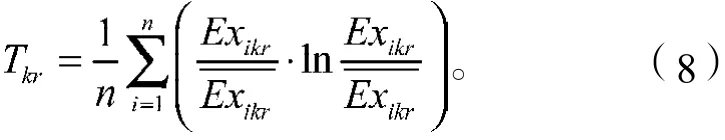
对式(8)进行变换得评估指标Ck的Theil不均衡指数Tkr为
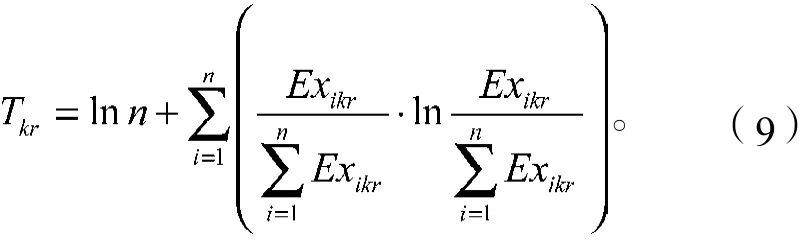
依据上述不均衡指数Tkr求得二级指标Ck的权重系数为
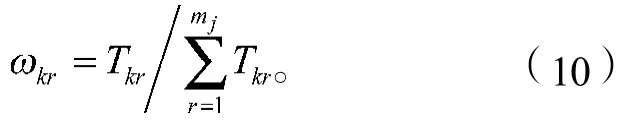
3.4 云集结和方案排序
1)利用云加权算术平均(normal cloud weighted arithmetic averaging,NCWAA)算子[21]
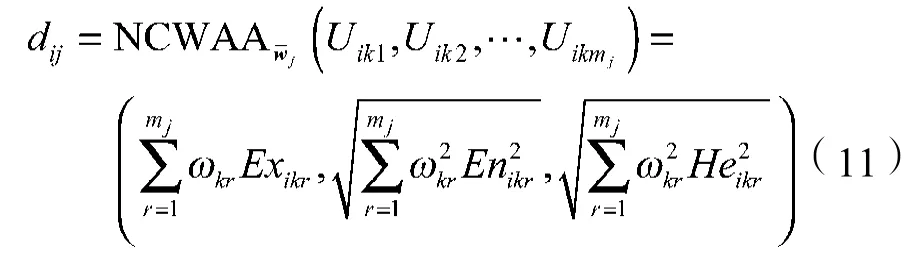
对云决策矩阵Aj中第i行的指标值进行集结,得到投资项目Xi关于一级指标Bj的评价值
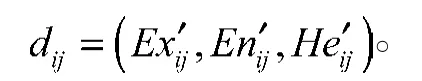
2)设一级指标Bj的权重向量为,其中wj≥0,。则利用Theil指数可求得该权重向量w,其中:
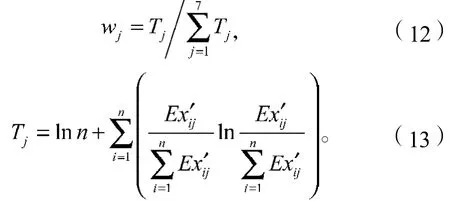
3)利用NCWAA算子
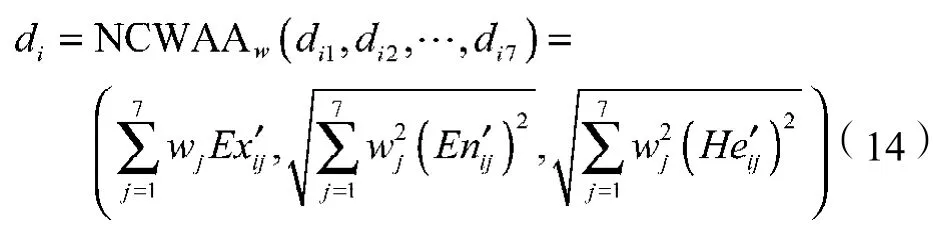
对各一级指标值进行集结,得到投资项目Xi的综合评价值。
4)利用文献[22]给出的云模型排序方法对所有投资项目进行排序。
由云模型的定义可知,d=(1, 0, 0)为最优云。投资项目Xi的综合云与最优云的相对贴近度Di、模糊性相对贴近度FDi和随机性相对贴近度RDi可由下列公式计算:
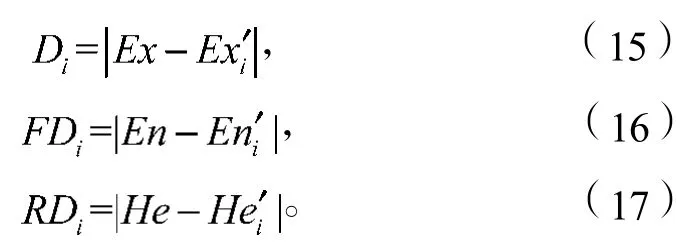
根据Di, FDi和RDi,利用以下法则可对所有投资项目进行排序,排在最前面的云模型所代表的方案就是最优方案:
①按距离相对贴近度Di的大小对方案进行排序,Di越小的项目,该投资项目风险越小,该投资方案就越好;
②对于具有相同距离相对贴近度的方案,根据模糊相对贴近度FDi比较方案优劣,FDi越小的项目,该投资项目风险越小,该投资方案就越好;
③对于具有相同距离贴近度和模糊相对贴近度的方案,根据随机性相对贴近度RDi比较方案优劣,RDi越小的项目,该投资项目风险越小,该投资方案就越好;
④对于3个数字特征都相同的方案,认为其方案没有优劣之分。
综上所述,基于云模型和Theil指数的投资项目风险评估的具体步骤如下:
第1步 制定二级指标Ck的评分标准,根据指标评分标准,由p位专家按10分制给每个项目的每个二级指标Ck用区间数打分,得到第l位专家给投资项目Xi的第k个二级指标的区间评价值;
第2步 利用式(1)~(7)计算得到投资项目Xi关于第k个二级指标的综合云和各一级指标Bj下的云决策矩阵
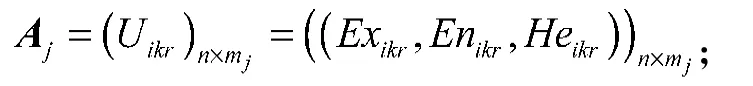
第3步 利用式(8)~(10)计算一级指标Bj下的各二级指标Ck的权重向量
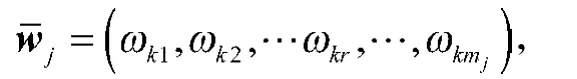
其中kr≥0;
第4步 利用式(11)对云决策矩阵Aj中第i行的指标值进行集结,得到投资项目Xi关于一级指标Bj的评价值;
第6步 利用式(14)对各一级指标值进行集结,得到投资项目Xi的综合评价值;
第7步 利用式(15)~(17)计算投资项目Xi的综合评价值与最优云的相对贴近度Di、模糊性相对贴近度FDi和随机性相对贴近度RDi。
第8步 利用相对贴近度Di、模糊性相对贴近度FDi和随机性相对贴近度RDi对各方案进行排序,并选择最优方案。
4 算例
选择某IT行业跨国公司拟投资的4个风险投资项目,分别对这4个项目进行综合评估,为决定是否投资提供依据。评估决策过程如下:
第1步 对这4个投资项目二级指标评分,得到5位专家(专家权重)对每个投资项目的二级指标值的区间评价值,由于篇幅所限,文中不再给出。
第2步 利用式(1)~(7)计算4个投资项目每个二级指标的综合云,见表2。
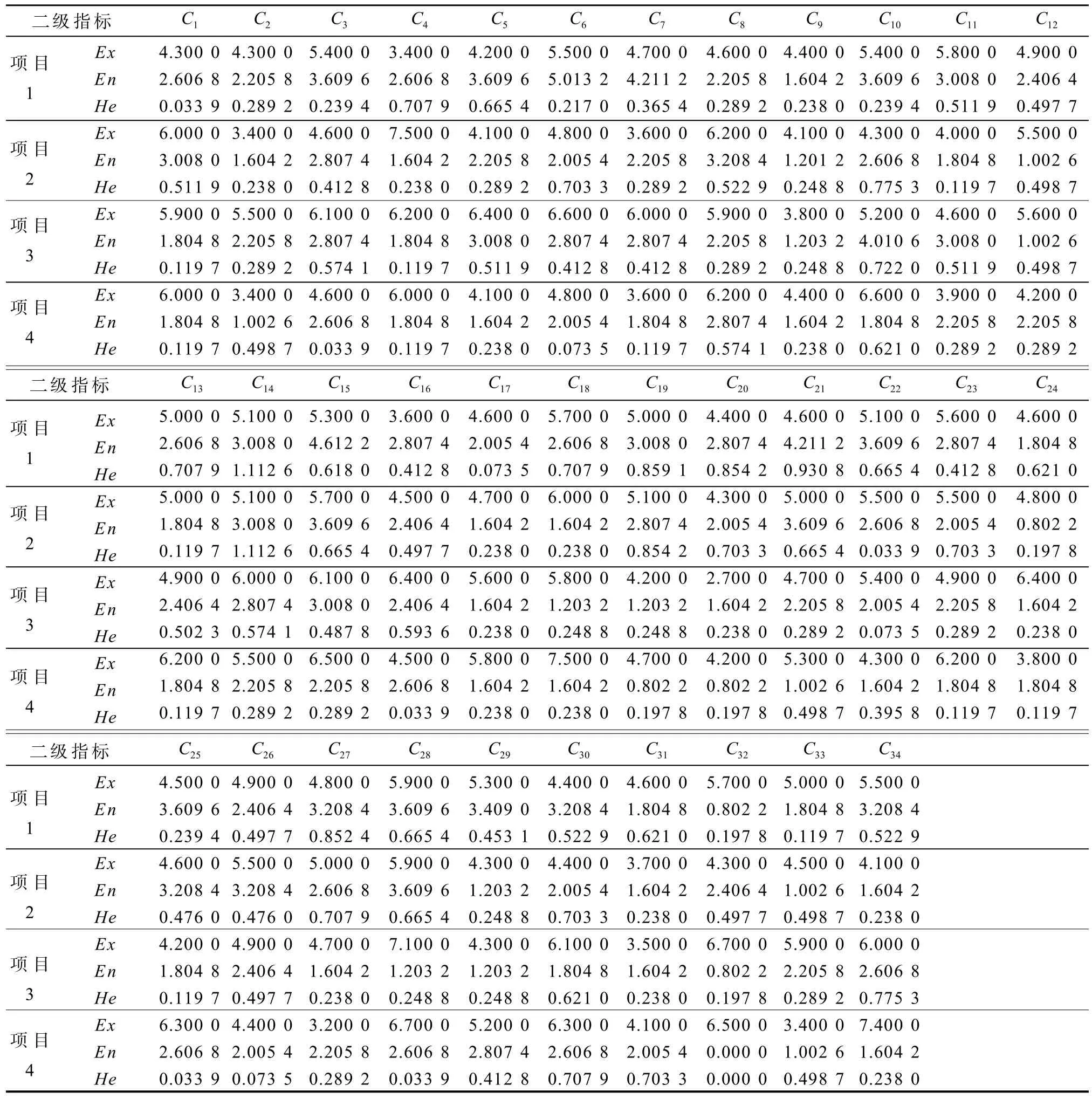
表2 二级指标的综合云Table2 Comprehensive clouds of the second-level indexes
第3步 利用式(8)~(10)计算出二级指标的权重:

第4步 利用式(11)计算得到第i个投资项目关于一级指标Bj的评价值
<1),且各件产品是否为不合格品相互独立.
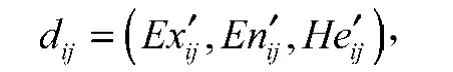
见表3。
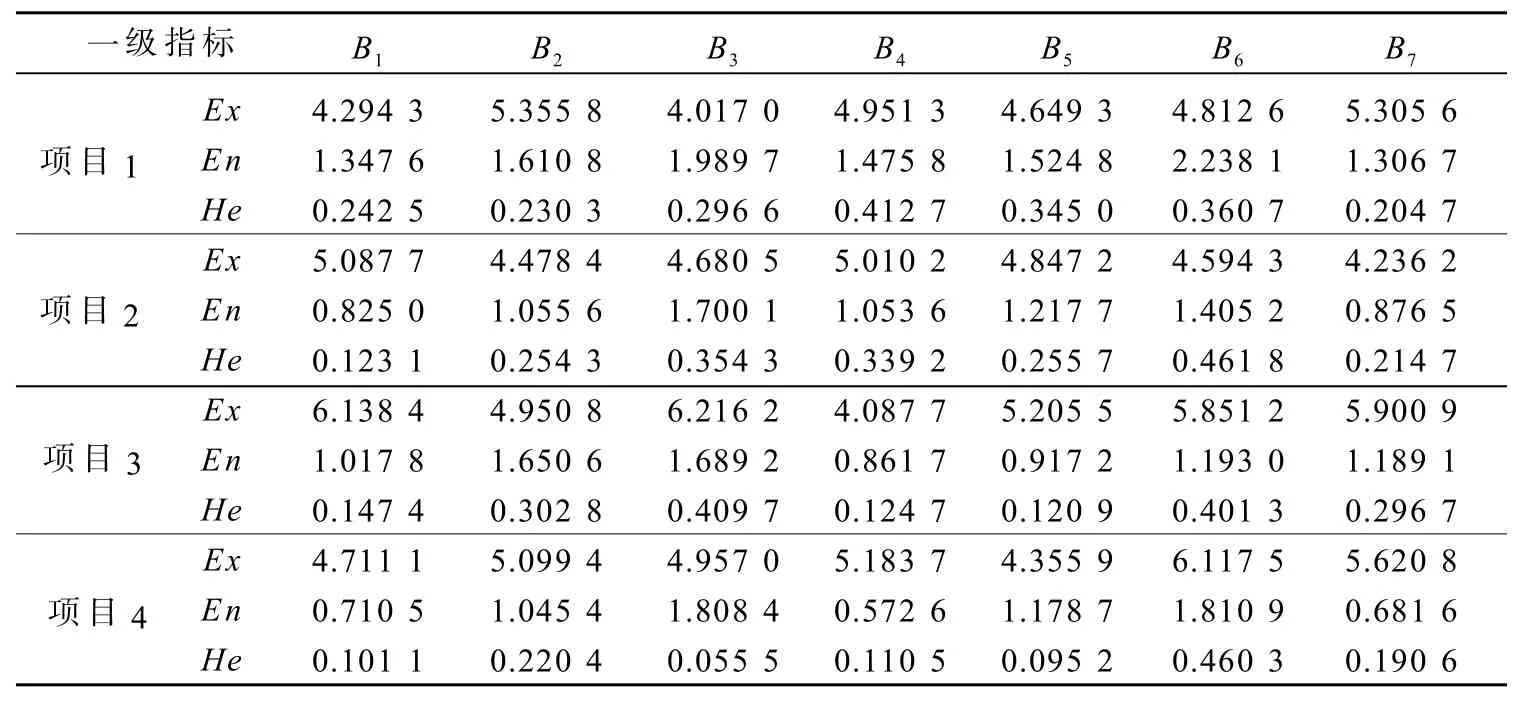
表3 一级指标的评价值Table3 Assessment values of the first-level indexes
第5步 利用式(12)和(13)求得一级指标的权重向量
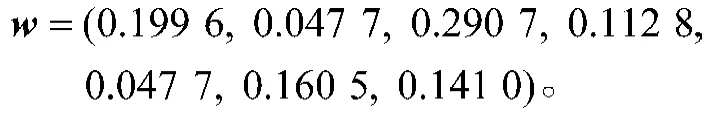
第6步 利用式(14)对各一级指标值进行集结,得到4个投资项目的综合评价值:

第7步 利用式(15)~(17)计算4个投资项目的综合评价值与最优云的相对贴近度、模糊性相对贴近度和随机性相对贴近度:
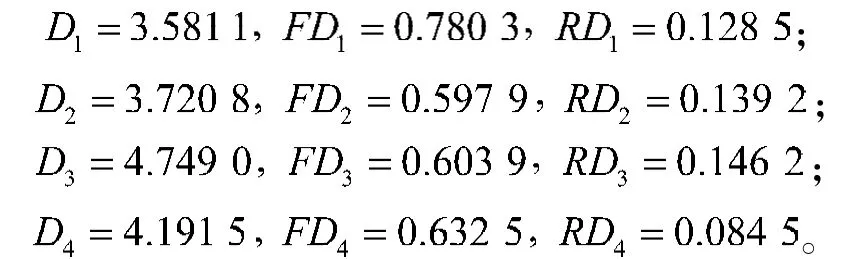
第8步 利用相对贴近度、模糊性相对贴近度和随机性相对贴近度对各方案进行排序,得到:项目1项目2项目4项目3。因此,最佳选择是项目1。
5 结语
本文根据我国风险投资的实际情况,构建了投资项目风险评估的三级评估指标体系,提出了基于云模型和Theil指数的投资项目风险评估方法。该方法首先将各指标值转化为云模型,以指标信息的不均衡度为基础确定指标权重,基于此权重进行云模型集结和综合评估。实例应用表明,该方法是可行和有效的,其中对评估指标进行区间估计,符合指标评估打分的波动性;利用云模型进行计算,能有效避免丢失信息;同时通过Theil不均衡指数计算指标权重值,能够有效抑制主观赋权法中主观随意性带来的评估误差,使评估结果更客观合理。本方法能提高风险投资项目评估的有效性,进而提高投资的成功率。
[1] 王世波,崔金鉴,王世良. 基于层次分析法的风险投资项目评价[J]. 工业技术经济,2003(6):87-94. Wang Shibo,Cui Jinjian,Wang Shiliang. Venture Investment Project Evaluation Based on AHP[J]. Industrial Technology & Economics,2003(6):87-94.
[2]Wells W A. Venture Capital Decision Making[D]. Carnegie :Mellon University,1974.
[3]Poindexter J B. The Efficiency of Rinancial Markets: The Venture Capital Case[D]. New York:New York University, 1976.
[4]Tyebjee T T,Bruno A V. A Model of Venture Capitalist Investment Activity[J]. Management Science,1984,30 (9):1051-1066.
[5]Macmillan I C,Siegel R,Subba Narasimha P N. Criteria Used by Venture Capitalists to Evaluate New Venture Proposals[J]. Journal of Business Venturing,1985,1(1):119-128.
[6]Fried V H,Hisrich R D. Toward a Model of Venture Capital Investment Decision Making[J]. Financial Management,1994,23(3):28-37.
[7]Kaplan S N,Stromberg P. Venture Capitalists as Principals: Contracting, Screening, and Monitoring[J]. American Economic Review,2001,91(2):426-430.
[8]Kakati M. Success Criteria in High-Tech New Ventures[J]. Technovation,2003,23(5):447-457.
[9]成思危. 中国经济改革与发展研究[M]. 北京:中国人民大学出版社,2001:1-98. Cheng Siwei. Study on Chinese Economic Reform and Development[M]. Beijing:Renmin University of China Press,2001:1-98.
[10]刘常勇,段 樵,伍凤仪. 创业投资评估决策程度[J]. 中外科技政策与管理,1996(12):64. Liu Changyong,Duan Qiao,Wu Fengyi. Venture Investment Decision Level[J]. Science & Technology Policy and Management,1996(12):64.
[11]汤京华,王玉珍. 风险投资项目评估指标体系的研究[J].北京工业大学学报,1999,25(12):42-44. Tang Jinghua,Wang Yuzhen. Research on Evaluation Index System of Venture Investment Project[J]. Journal of Beijing Polytechnic University,1999,25(12):42-44.
[12]周乃敏. 高技术风险投资公司择项的评价指标体系研究[J]. 技术经济与管理研究,1999(2):36-37. Zhou Naimin. Study on the Evaluation Index System of Project Selection for High Technology VC Firm[J]. Technoeconomics & Management Research,1999(2):36-37.
[13]寸晓宏. 营造完善的风险投资外部环境[J]. 中南财经大学学报,2000(4):65-68. Cun Xiaohong. Establishing Perfect External Environment of Venture Investment[J]. Journal of Zhongnan University of Finance and Economics,2000(4):65-68.
[14]邹辉文,陈德锦,张玉臣,等. 风险投资项目的终选方法和评估指标[J]. 科研管理,2002,23(5):104-109. Zou Huiwen,Chen Dejin, Zhang Yuchen, et al. Some Methods and Evaluating Indexes of Ultimate Choice of Projects for Venture-Capital Investment[J]. Science Research Management,2002,23(5):104-109.
[15]张春英,姜 丹. 高新技术风险投资项目评估定量模型研究[J]. 科学管理研究,2001,19(5):69-72. Zhang Chunying,Jiang Dan.Study on the Quantitative Model to Evaluate the High-Tech Risk Investment Project [J]. Scientific Management Research,2001,19(5):69-72.
[16]陈 静,李锦飞,翁肖力. 高新技术投资风险与风险管理[J]. 江苏大学学报:社会科学版,2001(1):71-73. Chen Jing,Li Jinfei,Weng Xiaoli. Investment Venture and Risk Management of High-Technology[J]. Journal of Jiangsu University:Social Science Edition,2001(1):71-73.
[17]Li D,Cheung D,Shi X M, et al. Uncertainty Reasoning Based on Cloud Models in Controllers[J]. Computers and Mathematics with Applications,1998,35(3):99-123.
[18]万树平. 运用Theil不均衡指数进行模糊传感器数据融合[J]. 计算机工程与应用,2009,45(3):133-134. Wan Shuping. Fuzzy Multi-Sensor Data Fusion Using Theil Disequilibrium Index[J]. Computer Engineering and Applications,2009,45(3):133-134.
[19]李德毅. 不确定性人工智能[M]. 北京:国防工业出版社,2005:1-245. Li Deyi. Artificial Intelligence with Uncertainty[M]. Beijing :National Defence Industry Press,2005:1-245.
[20]于少伟,李修海,刘庆玲. 基于区间分析和云模型的实物期权定价研究[J]. 山东大学学报:理学版,2010,45 (5):64-68. Yu Shaowei,Li Xiuhai,Liu Qingling. On Real Option Pricing Based on Interval Analysis and the Cloud Model [J]. Journal of Shandong University:Natural Science,2010,45(5):64-68.
[21]王坚强,杨恶恶. 基于蒙特卡罗模拟的直觉正态云多准则群决策方法[J]. 系统工程理论与实践,2013,33(11):2859-2865. Wang Jianqiang,Yang Wue. Multiple Criteria Group Decision Making Method Based on Intuitionistic Normal Cloud by Monte Carlo Simulation[J]. Systems Engineering-Theory & Practice,2013,33(11):2859-2865.
[22]王洪利,洪玉强. 基于云模型具有语言评价信息的多属性群决策研究[J]. 控制与决策,2005,20(6):679-681. Wang Hongli, Hong Yuqiang. On Multiple Attribute Group Decision Making with Linguistic Assessment Information Based on Cloud Model[J]. Control and Decision,2005,20(6):679-681.
(责任编辑:邓光辉)
On Risk Assessment of Investment Projects Based on the Cloud Model and Theil Index
Wang Xinfan1,Wu Xingkui2
(1. School of Science,Hunan University of Technology,Zhuzhou Hunan 412007,China;2. School of Finance & Economics,Hunan University of Technology,Zhuzhou Hunan 412007,China)
A risk evaluation index system is established for assessing investment projects from seven respects, such as the entrepreneur and team risk, product risk, technology risk, market risk, exit risk, policy and industry risks and regional influence, and a risk assessment approach based on the cloud model and Theil index is proposed. The evaluation indexes are transformed into cloud models, the weights of all indexes are calculated by using the cloud characteristics and Theil indexes, and on the basis of the weights, the cloud models are aggregated for deriving the comprehensive evaluation values of each alternative, and then the best alternative can be selected. Finally, the application of this method shows that it is feasible and effective.
investment project;risk assessment;cloud model;Theil index
C934
:A
:1673-9833(2014)01-0001-07
2013-12-24
教育部人文社科基金资助项目(12YJA630114),湖南省自然科学基金资助项目(11JJ6068),湖南省科技计划基金资助项目(2012FJ3036,2012FJ4116),湖南省高等学校科学研究基金重点资助项目(12A042)
汪新凡(1966-),男,湖南安化人,湖南工业大学教授,硕士生导师,主要从事决策分析,信息融合及风险控制的研究,E-mail:zzwxfydm@126.com
10.3969/j.issn.1673-9833.2014.01.001

