孔隙水压力在滑坡泥石流起动和运动中的作用*

周公旦

副研究员，中国科学院山地灾害和地表过程重点实验室，中国科学院水利部成都山地灾害与环境研究所，成都 610041

*国家自然科学基金(41201012)资助

孔隙水压力在滑坡泥石流起动和运动中的作用*

周公旦

副研究员，中国科学院山地灾害和地表过程重点实验室，中国科学院水利部成都山地灾害与环境研究所，成都 610041

*国家自然科学基金(41201012)资助

孔隙水压力；滑坡；泥石流

自然界重要的山地灾害——滑坡、泥石流都是由大量的颗粒物质和颗粒间孔隙水所构成的多相介质。颗粒间孔隙水压力的发展和消散直接影响颗粒间的作用，是导致边坡失稳、土体滑动、泥石流流动性加强的重要因素。全面综述孔隙水压力的定义和测试方法，孔隙水压力的发展、消散过程，以及颗粒间有效应力的变化，以期进一步明确孔隙水压力对滑坡、泥石流起动和运动的重要性。

滑坡、泥石流是世界范围内广泛存在的地质现象，它们都是由大量固体颗粒和颗粒间孔隙水(非饱和情况还包括部分孔隙气体)所组成的多相介质。现阶段，人们一般认为边坡内部固体颗粒间的相互咬合作用的弱化是导致颗粒间剪切滑移，以及由此进一步发展贯通所导致的大规模滑坡现象的关键因素。滑坡产生的大量松散固体物质和沟道洪水一起受重力的驱动很容易充分地掺混，且能在沟谷中或者坡地上快速地流动，形成高速远程的泥石流。颗粒间的摩擦、碰撞是影响泥石流流动性的关键因素。由此可见，颗粒间的作用对滑坡、泥石流的形成和运动非常重要。对于多相介质而言，固体颗粒间的作用完全受制于颗粒间孔隙水的影响，其中尤以孔隙水压力(pore water pressure)为第一要素。本文系统地介绍孔隙水压力的基本概念，全面回顾人们认识孔隙水压力的发展和消散对滑坡产生重要影响的过程，进而分析孔隙水压力对泥石流流动性的影响，以期能够帮助人们认识常见的山地灾害——滑坡、泥石流的自然规律。

1 孔隙水压力在土力学中的定义和作用

有效应力(effective stress)是现今被广泛接受的可用于描述土体力学行为的基本概念，亦是现代土力学中最重要的力学概念。追溯现代土力学的发展历史，我们可以发现，Terzaghi 在1920年左右率先提出了“有效应力”概念的雏形[1]，并且于1936年第一届国际土力学与基础会议(First International Conference on Soil Mechanics and Foundation Engineering)上进一步做了较为全面的阐述[2]。自此Terzaghi一举奠定了现代土力学的基础，同时也被尊称为“土力学之父”。Terzaghi 解释道，土体中某一断面上任意一点的应力状态可以由作用于其上的三个主应力σ1、σ2和σ3(总应力)计算而得。对于土颗粒间孔隙由水所填充的饱和土，三个主应力可进一步分解为两个部分：其一，由孔隙间水承担的各向同性的孔隙水压力uw；另外则是由土颗粒间相互咬合所组成的颗粒体系所承担的应力。其三个主应力分别为

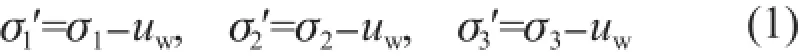
这部分直接由颗粒体系所承受的作用力(σ1′、σ2′、σ3′)，在土力学中称之为“有效应力”。

由于孔隙水本身的压缩模量很大(一般可认为水这种流体是不可压缩的)，因此孔隙水受力而导致的变形量很小。这种微小的变形不会进一步影响到土颗粒体系结构的重新排布、受力变形和破坏。同时，土颗粒体系中各个不同形状的颗粒亦可以被认为是本身不可压缩的，并且土颗粒和孔隙水的相互接触也可认为是完全光滑的。由此可知，土体本身的受力和变形只同其内部有效应力(σ1′、σ2′和σ3′)的改变相关，尽管这些有效应力严格意义上只能算是假想量(deduced quantity)，而不是真正的物理量，没有办法通过仪器直接测量。但显然，根据式(1)的解释，对土体的本构关系(stress-strain relationship)、强度(strength)以及稳定性(stability)等的研究可以从分析土体外部受力状况(即总应力σ1′、σ2′和σ3′)和土体内部的颗粒间孔隙水压力uw开始。

在实际的岩土工程中，土体孔隙水压力uw的计算往往会遇到以下几类情况：

(1)静止水压力

土颗粒之间的孔隙完全由水充满，并且整个颗粒体系和孔隙水都保持平衡状态，孔隙水在土体内部没有流动的状况。此时的孔隙水压力完全等同于由水自身重力所引起的位置水头(elevation head)。

(2)动水压力

土颗粒之间的孔隙完全由水充满，并且整个颗粒体系保持平衡状态(土体没有变形)，但是孔隙水在土体内部有恒定流动(steady flow)的状况(图1)。任意地从图 1试样土中选取上下相邻的两个点A和B，其两侧和两支测压管相连。根据伯努利方程，且忽视孔隙水流动速度，可知

A点孔隙水压力为

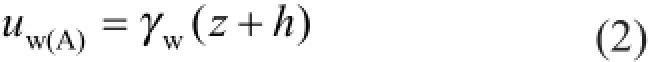
B点孔隙水压力为

则B点和A点的孔隙水压力的差值为

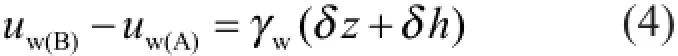
式(4)包含两个部分：其一为A点和B点的位置水头的差值，即γwδz；其二为水流在土体内部流动所导致的偏离位置水头的部分，可称之为超孔隙水压力(excess pore water pressure)，即γwδh，也可称之为渗透压力(seepage pressure)。流体在土颗粒间从B点到A点恒定地流动需克服摩阻力(frictional drag)而消耗一定的能量。为考虑水流沿程的能量损耗和孔隙水压力的变化，土力学中往往采用渗透力(seepage force) js和水力梯度(hydraulic gradient) i的概念来进一步计算这种摩阻力的大小。

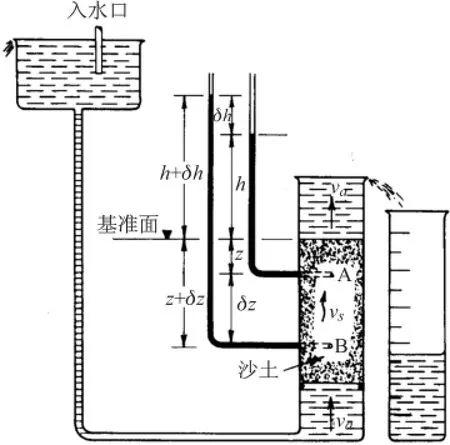
图1 渗透试验装置[3]

Darcy经验性定理(1856)[4]进一步表明：水流在饱和的土体中渗流，如果其紊动程度很小并可认为是层流时(雷诺数Re小于2000)，那么相应的渗透速度u同水力梯度成正比：

其中k是土体的渗透系数(hydraulic permeability)，同土体的结构和密实度紧密相关：土体越密实，孔隙率e越小，则k值越小。μ是孔隙水的黏度。

(3)土体变形引起的超孔隙水压力

上面考虑的是孔隙水在土颗粒骨架中的恒定流动且土骨架保持平衡的状况。实际状况是，孔隙水被包裹在由土颗粒所组成的骨架中，形成一个个相互联通且相对封闭的系统；土颗粒有效应力的改变是会导致土骨架的变形和重组的，这样包裹在土骨架中的孔隙水由于孔隙体积的变化(收缩或者膨胀)会引起孔隙水压力的变化，其中偏离原来位置水头的部分同样可称之为超孔隙水压力(excess pore water pressure)。这样的超孔隙水压力同样可以是正的，也可以是负值。外荷载是如何直接传递给孔隙水和土颗粒承受的，以及传递的比例都同外荷载施加的方式和速率有关。现代土力学研究发现[3,5]，对任何饱和的重构土(restructured soil)，都存在唯一的孔隙比e和有效应力 σ′之间的关系曲线，称之为临界状态线(critical state or steady state line)(图 2)。原始稳定状态的土体在图2的e-σ′空间中(或者υ-lnP空间；υ=1+e, P=(σ1+σ2+σ3)/3)，都是远离临界状态线的，而其受力变形直至破坏的过程就是不断向临界状态线趋近的过程。如果土体处于临界状态线上，那么意味着土体随着剪切应变εq的发展，强度q、体积应变εv、有效应力p′都不会再变化了，也可以基本认为是土体达到破坏状态了：

在这个过程中，如果土体原始状态点在临界状态线右上部(图2)，那么土体在缓慢剪切变形的过程中，将始终保持剪缩(contraction)的状态；而如果剪切变形速率较快，孔隙水来不及从土颗粒孔隙中向外排出，超孔隙水压力Δu为正(＞0)。相对应地，如果土体原始状态点在临界状态线左下部(图2)，那么土体在缓慢剪切变形的过程中，将始终保持剪胀(dilation/swelling)的状态；而如果剪切变形速率较快，孔隙水同样来不及从土颗粒孔隙中向外排出，超孔隙水压力Δu为负(＜0)。一般在岩土工程中，正常固结(normally consolidated)或者轻微超固结(slightly overconsolidated)的黏土(clays)和饱和的松砂(saturated loose sands)都是剪缩的(contractive)；而超固结的黏土(over-consolidated clays)和密砂(dense sands)具有剪胀(dilative)的特性。这里需要强调的是，实际的土体在受剪切破坏的过程中，排水或者不排水的状况是相对的，这是比较了土体剪切变形的速率和超孔隙水压力Δu消散速率后得出的。实验室进行的三轴试验采用不透水膜和连接土体的闸阀来严格控制排水条件只是更好地抽象科学的实际问题，这对机理研究很重要，但并不表明实际问题中是严格的不排水或者排水。在不排水主导的情况下，土体体积应变和孔隙率是保持不变的，土体只能通过产生超孔隙水压力来改变土颗粒间的有效应力(土力学中定义形变压缩为正，即δυ＞0；膨胀为负，即δυ＜0)。

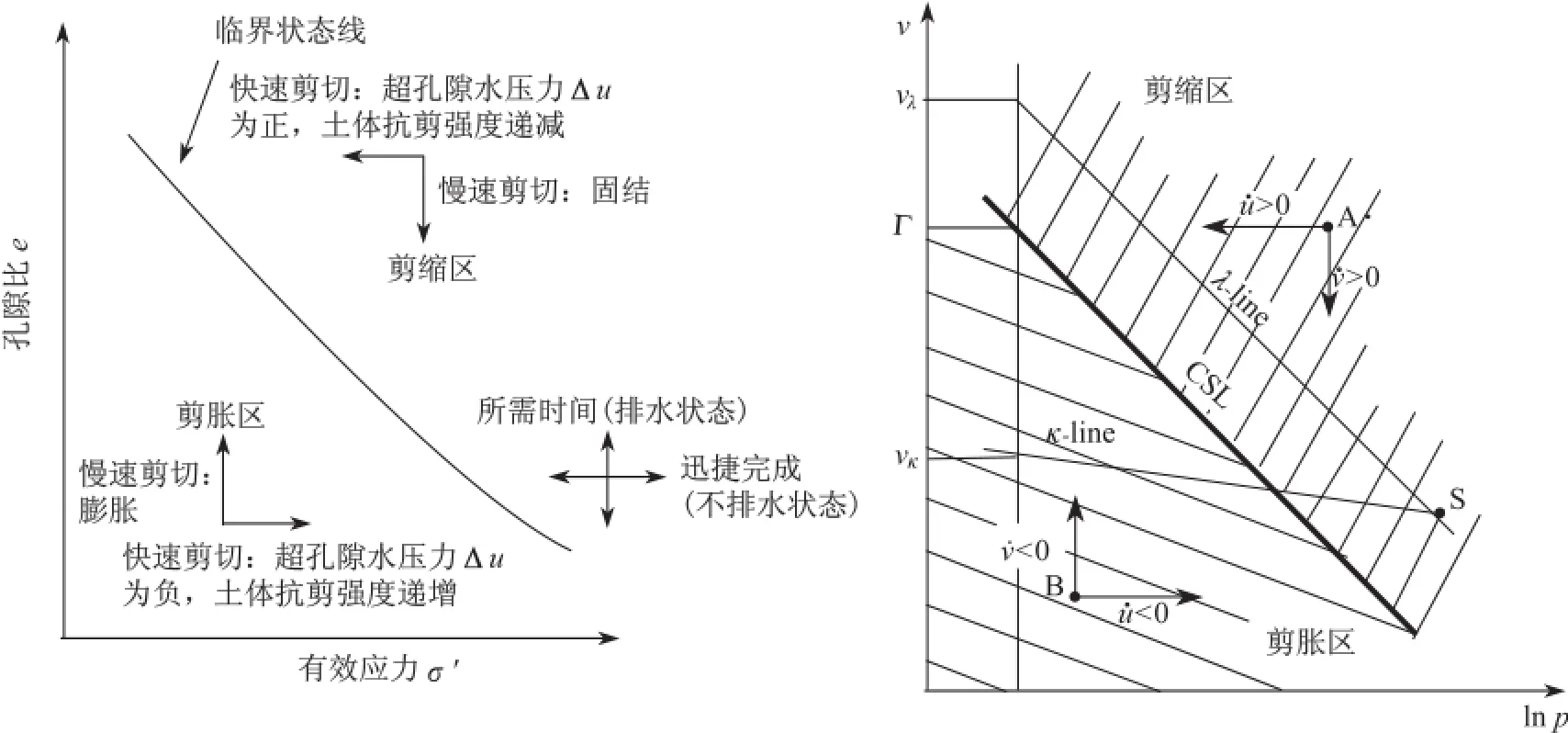
图2 原始应力状态点同临界状态线(CSL)的关系以及由此所导致的应变过程和孔隙水压力的不同发展[5]

2 泥石流和滑坡起动阶段的经典土力学原理

泥石流(debris flow)是一种由大量的颗粒物质与水(以及少量的气体)充分掺混后在重力作用下沿着山坡沟谷向下剧烈倾泻的地质现象，其流态往往是复杂多变的。泥石流区别于岩崩(rock avalanche)和一般的挟沙水流(sediment-laden water floods)最关键的地方是泥石流的流动性受颗粒间的相互作用和孔隙水的影响都非常大，它们是决定泥石流流变特性(rheological property)的两大关键因素[7]。不同于呈流态状的泥石流，滑坡(slope failure)一般可近似地看做是土体沿着滑裂面的刚体运动(即滑动体内部组织和结构都变化不大)，其运动距离较泥石流来得小，一般不具有流变的特性(图3)。泥石流在很多情况下是滑坡逐渐演化来的，尤其是强降雨引发的滑坡-泥石流。故此，两者虽有着明显的区别，但联系又是非常地密切。国际学术界对泥石流和滑坡在不是很明确的情况下一般可以统称为 “landslide”。当前滑坡向泥石流演化的过程是研究的热点，也是难点。

泥石流和滑坡起动阶段都是边坡土体失稳的过程，这中间离不开孔隙水压力的作用。

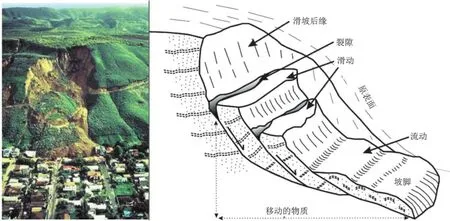
图3 滑坡运动过程及向泥石流的演化示意图[6]

孔隙水在边坡土体内的渗透是导致边坡失稳的很重要原因。其中渗透水流动方向、土体强度参数、土层厚度，以及边坡坡度等对边坡稳定性的影响有些是很清楚的，有些则是可以通过概率的方法加以确定。通过计算边坡安全系数，对影响边坡稳定性的不同参数作敏感性分析是可以实现的。尤其对饱和的土质边坡，分析渗透水的流动方向角度(seepage flow angle)是很重要的。Iverson[8]提出的均质(hydraulically isotropic soil)边坡稳定性分析的方法比较具有普遍的意义，其中孔隙水在边坡体内的渗透所导致的孔隙水压力和渗透力的分布和发展对边坡稳定性的影响是巨大的，对滑坡的形成和起动起着至关重要的作用。现阶段大家对降雨和边坡失稳之间的关系有了大致的理解，尽管这个理解还不是很到位。主要是对降雨强度和持续时间(包括前期降雨，antecedent rainfall)同雨水在地表的渗透(infiltration)所导致的边坡体内水位面(G. W. L.)的变化以及进一步的孔隙水渗透作用之间的关系还不是很清楚，具体的就是降雨条件和影响边坡稳定性的那些基本参数间的关系尚不明确。其中至关重要的当然就是土体孔隙水压力的变化，因为它直接影响着能够决定土体力学行为的有效应力的大小。

在滑坡向泥石流转化的过程中，边坡面上土层收到上部滑坡体强烈而快速的剪切运动时，其内部超孔隙水压力将快速增大但又不能及时消散，可认为是一种不排水的情况。快速增大的超孔隙水压力是导致土体“液化”并且失稳的关键因素。通过野外的观察和室内的土力学实验，日本京都大学的Sassa教授和其团队对滑坡向泥石流演化的机理方面作了比较深入的研究[9-12]。他们认为：一个流域的沟谷坡道上往往堆积了大量的前期滑坡、崩塌以及水利类搬运所形成的饱和松散固体颗粒物质(torrent deposit)；当上部滑坡体(failed mass)快速经过这些松散堆积体的时候一定会对下部土层产生强烈的剪切作用，这种快速的剪切运动作用于饱和的松散堆积土层时，土颗粒结构的剪缩(contraction)现象马上发生，从而导致很大的超孔隙水压力uΔ，进而引起堆积土层的“液化”，土体强度几乎消失；堆积体开始向下剧烈流动，其龙头往往导致下游更多的松散堆积土的液化，并掺混进入泥石流体内，使其规模快速增大。

除了上述整体性的液化(mass liquefaction)外，很多时候可以发现滑坡体是沿着某一个滑动面(slip surface)高速运动的。在滑动面附近存在一个强烈的剪切层(shear zone)，其中的应力很大，剪切速率很高。这种快速的剪切运动对于饱和的剪切层土体同样容易导致超孔隙水压力的发展，以致其相应的有效应力趋近于零，发生滑动性的液化(sliding-surface liquefaction)，然后迅速地演化成流动性很大的滑坡-泥石流。图 4 勾画了整体性和滑动边界面上的两种液化的应力路径，其共同点都是由于局部土颗粒骨架所构成的空间的体积压缩，从而引发被包裹的孔隙水压力的激增，进而导致土颗粒间的有效应力和土体剪切强度的衰减。

3 泥石流运动阶段中孔隙水压力的重要性

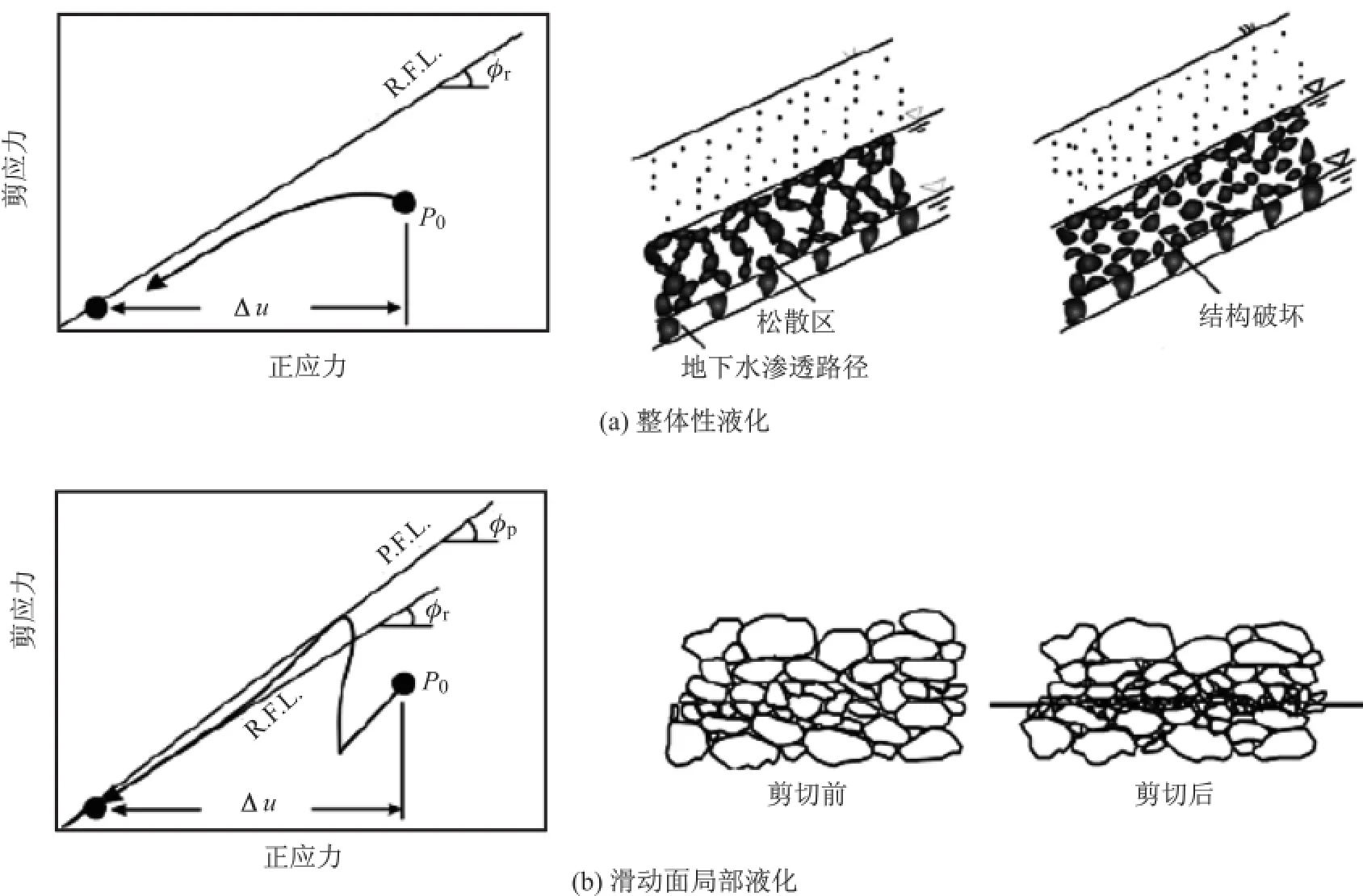
图4 整体性液化(a)和滑动面局部液化(b)示意图和机理解释[13](其中P. F. L. 是极限强度线，R. F. L. 是残余强度线，p0是原始应力状态点，Δu是超孔隙水压力，φp和φr分别为对应于极限抗剪强度和残余抗剪强度的内摩擦角)

上面叙述的孔隙水压力在土力学中，尤其是在滑坡、泥石流起动阶段的重要性是基于充分的物理实验和理论分析而得出的。土力学中孔隙水被土颗粒骨架所包裹，土颗粒这种持续性的接触是运用连续介质力学来描述散粒体材料力学性质的基本前提。尽管土体受力变形的过程中应变数值不是很大(基本属于小变形的范畴)，但孔隙水压力的变化受土颗粒孔隙体积的变化却是很大的，以至于有液化现象的发生。

泥石流是大量的固体颗粒同水充分掺混，一起沿着沟谷坡道剧烈运动的过程。泥石流颗粒物质之间的接触作用往往是短瞬间完成而不是持续的，因此，很长时间内广大的泥石流研究者所困惑的一个问题是，泥石流颗粒间是不是也能形成一定的组织和结构，使得被其包裹的孔隙水压力也会随着孔隙空间的压缩或者膨胀而产生超孔隙水压力。这样的超孔隙水压力又反过来影响颗粒间的有效应力和泥石流整体的流动性。泥石流孔隙水压力的测量相比于一般土力学实验中的测量，难度可想而知，但它是解开上述泥石流研究所面临的科学难题的关键。这方面，美国地质调查局(USGS) Iverson博士的研究为我们找到了初步的答案[7]。

图5(a)显示的是美国地质调查局在俄勒冈州修建的大型泥石流实验用水槽，其尺寸为100 m长，2 m宽， 1.2 m高，坡度为31°(图5(b))。沿着水槽底部距离闸门32 m和67 m的地方安装了总应力和孔隙水压力的传感器，其相应的顶部安装了激光泥位机用以测量泥石流的泥深，进而可以推算泥石流底部的位置水头(图5(c))。进一步的测量结果可参见图5(d)某一次泥石流沿水槽起动后流动67 m后所形成的一阵泥石流(surge debris flow)经过传感器断面时留下的记录(其中第14 s是龙头刚刚通过的时刻)。实验和野外观测的结果相类似，每一次泥石流都包含很多阵的阵流，每一个阵流的龙头(front head)通常聚集着大量的块石以及少量的液体(图5(a)箭头所示)。实验结果表明泥石流龙头底部的孔隙水压力几乎为零；而在龙头随后的泥石流主体内部则聚集着大量的液体和细颗粒，在其底部所测得的孔隙水压力很大(图5(d))，甚至大到足以支撑其上部的土颗粒重量以至于很轻易就产生液化的现象[7]。这一结论已被泥石流野外观测的结果和分析所证实[17]。由此可知，泥石流体内颗粒物质的相互作用同样会导致局部超孔隙水压力的发展。它同颗粒的剧烈扰动(agitation，可用颗粒温度(granular temperature)的概念表示)一起，是影响泥石流流动性的重要因素[7]。

在描述泥石流流动的数学计算模型中，尽管对颗粒之间的接触和结构以及颗粒和孔隙水之间的相互作用的研究还不是很充分，细观和宏观之间还没有建立很好的联系；但是采用连续介质力学的方法(质量和动量的守恒)来描述泥石流仍是现阶段广泛采用的方法。其中Iverson博士的研究工作值得大家借鉴。Iverson[18]推导的泥石流一维动量守恒方程为

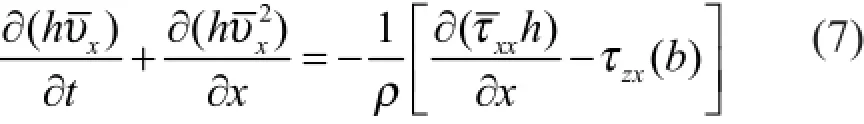
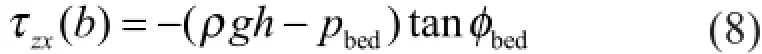
式(7)可进一步修正为

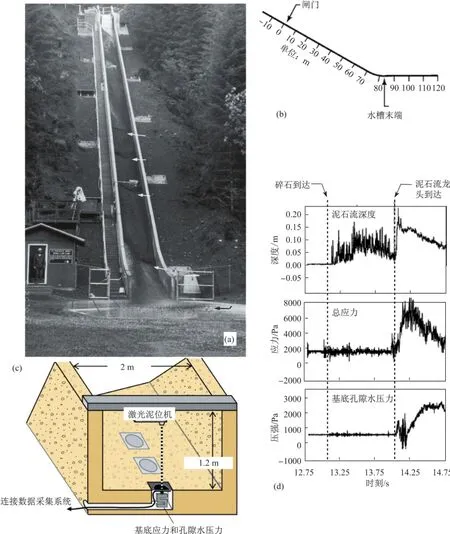
图5 美国地质调查局(U.S. Geological Survey) 的大型泥石流水槽实验[14]：(a) 泥石流实验过程[15]；(b) 大型水槽尺寸和结构[7]；(c) 泥石流传感器装置图[16]；(d) 泥石流运动过程中在水槽底部测量到的泥石流深度、总应力、孔隙水压力随时间的变化(传感器断面位于水槽闸门以下67 m处)[7]

这个简化的控制方程具有很明确的物理意义，即牛顿第二定律。对该控制方程的稳定性分析(stability analysis)可以进一步发现，任何浅水波形式的流体运动(shallow flows)都会由于惯性力和重力的相互作用(interaction of inertial and gravitational effects)而产生小规模的阵流，这同其本身的流变性质无关[19]；但每一阵泥石流的龙头规模会因为床面摩阻力分布的不均匀性变得越来越大。对这种摩阻力分布的不均匀性分析其原因，主要是龙头处颗粒的分选和孔隙水压力的消散[7](图7)。从式(9)可以很清楚地看到，泥石流在床面摩阻力的不均匀分布主要体现在右边第二项中，其中泥石流在床面处孔隙水压力pbed在空间尺度上的分布和在时间尺度上的消散是产生这种不均匀性的关键。受前面所介绍到的Darcy定理的启发(式(5))，超孔隙水压力的发展和消散同颗粒物质所形成的结构相关，尤其是土颗粒所表现的渗透性。然而，不同颗粒组分(grain-size distribution)的散粒体材料的渗透系数可以相差好几个等级，由此可推断，颗粒物质的分选可以极大地影响超孔隙水压力的变化，从而导致床面摩阻力的巨大变化。图7显示的是泥石流龙头颗粒分选的状况：大颗粒快速运动并聚集于泥石流体上部的自由表面和前缘(图7(a))；从横向观察可发现，泥石流沿中轴线向两侧推挤大颗粒物质(图7(b))，而中间主体部分则保留大量的饱和细小颗粒。由于这种复杂的颗粒间的分选作用，使得每一阵泥石流的龙头形状高陡且富含粗颗粒物质，并因缺乏大量的超孔隙水压力以至于床面摩阻力巨大；相反地，泥石流尾部段颗粒细小且充分饱和，较大的孔隙水压力使得土颗粒趋于液化状态，床面摩阻力小，运动速度自然较之于龙头要大。这种由床面摩阻力分布的不均所造成的泥石流体内运动速度的差异是放大泥石流阵性波的重要原因，尽管式(9)中所暗示的是泥石流厚度不断变小的趋势[18]。

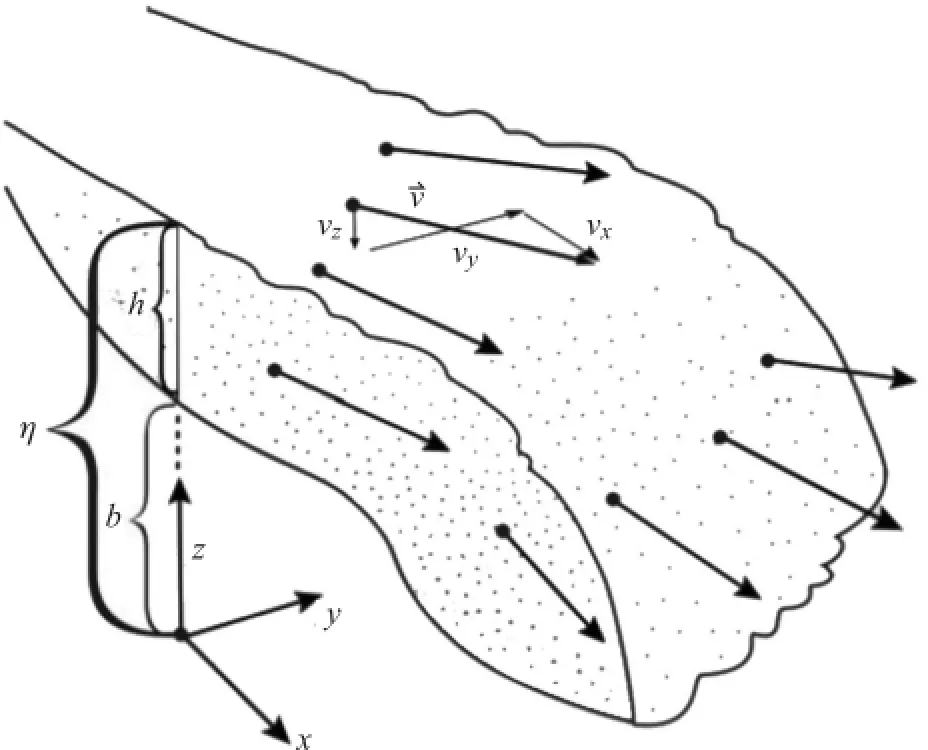
图6 泥石流沿坡面运动示意图[18]

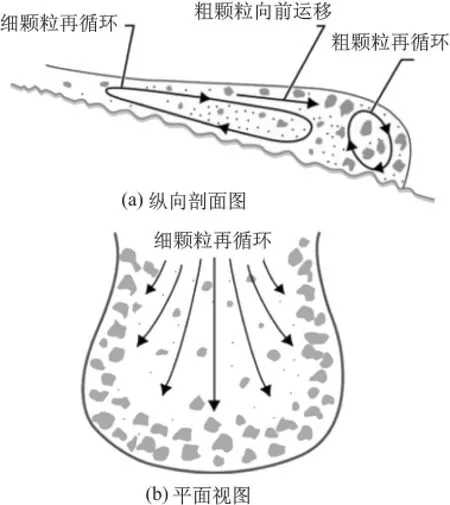
图7 泥石流龙头颗粒分选示意图[18]

泥石流运动主体(固液两相)同一般土体的变形相类似，即使其整体的变形或运动是恒定的，局部颗粒所组成的空间的剪胀和剪缩都会导致局部的超孔隙水压力数值的波动，进而影响局部的土颗粒间的有效应力[20]。如前面所述，土体排水或不排水状况取决于土体变形速率和超孔隙水压力的消散速率。同样地对泥石流，局部超孔隙水压力的发展和对周围颗粒体的影响取决于固体颗粒受剪切作用而重新排布的速率和孔隙水压力趋于平衡的速率(即超孔隙水压力的消散速率)。参考Iverson博士等的研究成果，这可以用一个无量纲数加以考虑和甄别[20]：

其中k是流体(水)在泥石流颗粒物质中的渗透系数(hydraulic permeability)，E是泥石流颗粒体的压缩模量(杨氏模量)，υs是泥石流中颗粒间的相对运动速度，µ是泥石流浆体的黏度，d50是泥石流颗粒物质的平均粒径。式(10)中kE/µ代表孔隙水压力的消散速率(diffusivity)，d2µ/(kE)则50是局部孔隙水压力经过d50的扩散路径而趋于平衡所需要的时间，d50/υs可代表颗粒体系变形(剪胀或剪缩)单位粒径所需要的时间。因此无量纲数NR的物理意义在于比较颗粒剪切运动的时间尺度和由此引起的局部超孔隙水压力消散的时间尺度的比值。当NR很大的时候，则表示泥石流在运动过程中超孔隙水压力尽管有所发展，但很快速地消散完毕，其影响有限；反之，如果NR数值很小，则说明超孔隙水压力在泥石流运动过程中没有足够的时间消散，将极大地影响颗粒间的相互作用。这样的定义其物理意义明确，对研究泥石流运动机理具有很重要的作用。

野外实际的泥石流所呈现的流态是变幻莫测的。世界著名的云南东川蒋家沟泥石流观测站多年观察到的泥石流主要分两种：阵性流(surge flow)和连续流(continuous flow)。其中区分它们的主要依据是人为判断的持续时间和流量，即当“阵与阵之间持续流量较大，或一阵持续时间很长时视为连续流；当阵与阵之间明显断流时视为阵性流”[21]。显然这样的认识还不够科学和全面。根据上述Iverson博士对泥石流孔隙水压力的理解[20]并参考野外泥石流观测的结果，Zhou和Ng[22]重新定义了一个无量纲的数：其中l是泥石流运动方向上的长度，可近似地等同于泥石流龙头移动速度U和泥石流持续时间t的乘积(即l=U·t)。同式(10)相比较，式(11)是采用泥石流的运动时间代替了颗粒体系变形(剪胀或剪缩)单位粒径所需要的时间d50/υs，并使用超孔隙水压力沿距离最短的深度方向的消散时间µh2/(kE)代替了局部孔隙水压力经过d50的扩散路径而趋于平衡所需要的时间µ/(kE)。这样式(11)对判断宏观的泥石流运动过程中孔隙水压力的作用具有更直观的效果，而物理意义同样比较明确：较小的Np数值表示的是在泥石流运动和发展过程中，超孔隙水压力没有足够的时间消散，将极大地影响颗粒间的相互作用。进一步地，Zhou和Ng[22]采用经典颗粒流的研究成果[7,23]，比较了泥石流运动过程中颗粒物质相互间的作用(尤其是颗粒间的剪切滑动和碰撞的相对重要性)，提出了修正的Savage数：

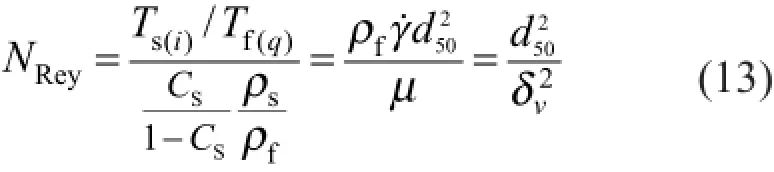
其中Ts(i)是颗粒碰撞引起的Bagnold惯性力，Ts(q)是颗粒层之间的剪切和滑动所产生的摩擦力，ρsρf分别为颗粒和水的密度，γ˙是泥石流体内的剪切速率，θ是坡角，φ′是泥石流颗粒间的内摩擦角。考虑到泥石流孔隙水对颗粒的作用不止局限于孔隙水压力，由于流体的流动对颗粒还有粘性拖曳力的作用(图8)，故此可借用水力学中判断层流和紊流的雷诺数的定义，提出泥石流的颗粒雷诺数(grain Reynolds number)的概念用以比较颗粒间流体的黏性对颗粒所施加的拖曳力和颗粒间碰撞所产生的惯性力的大小：

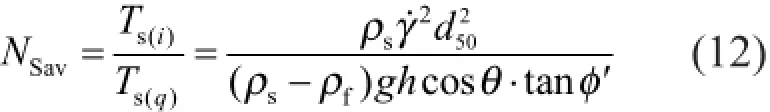
图8 流体绕过泥石流颗粒的示意图[22]

根据以上新定义的无量纲数，图9(a)和9(b)分别比较了Np和NRey、NSav之间的关系，找出了区分阵性流和连续流的明确边界线。其中根据Np的两个临界数值(0.01和0.03)，可以比较好地把蒋家沟泥石流区分为阵性流(Np＜0.01)、过渡性泥石流(0.01＜Np＜0.03)，以及连续流(Np＞0.03)。这样的区分同泥石流中阵性流和连续流所携带颗粒物质的不同能力是相一致的(即图9(c)所示的单位宽度输沙率和图9(d)所表示的颗粒体积浓度CS同Np的关系)。由图9进一步分析可知，阵性流颗粒物质浓度较连续流大，其单位宽度的输沙率也相应地要大许多。更重要的是，由于颗粒之间的结构紧密，阵性流运动过程中产生的超孔隙水压力较大且不容易很快地消散，在整个运动中始终发挥重要的作用，因此其对应的Np数值很小；相反地，由于连续流颗粒浓度较小，颗粒间结构稀疏，即使由于局部颗粒的重组产生了超孔隙水压力，但是同运动时间相比其超孔隙水压力消散所需的时间很少，因此在运动中不发挥重要的作用。这样的方法，不仅将野外观测的结果很好地做了系统性的归纳，更重要的是揭示了现象背后的物理机理，对进一步的研究具有科学的指导意义。

图9 采用无量纲数之间的相互对应关系对阵性泥石流和连续泥石流的划分[22]

4 结论和展望

对于由大量颗粒物质和颗粒间流体所构成的多相介质，滑坡、泥石流的起动和运动都受到孔隙水压力的巨大影响。正确认识孔隙水压力，尤其是超孔隙水压力的发展和消散，是掌握滑坡、泥石流等山地灾害触发机理和运动规律的关键。超孔隙水压力的本质是颗粒和孔隙水的耦合作用。现阶段，人们对滑坡起动阶段的超孔隙水压力的涨落和土体有效应力的变化认识比较到位，据此开发的本构模型能够比较准确地描述土体的力学行为；但对于滑坡向泥石流转化的阶段，以及泥石流运动阶段中的孔隙水压力涨落的认识还处于起步的阶段，主要原因是对颗粒流动过程中的颗粒间作用方式、颗粒结构、流固耦合作用等不是非常清楚，孔隙水压力的测试手段也有待改进。深入开展多相介质流动的物理模型和数值模拟，是揭示相关山地灾害演化过程的核心，是当前国际学术界研究的热点和难点。

(2014年9月3日收稿)■

[1] SKEMPTON A W. Significance of Terzaghi’s concept of effective stress [M]// Bjerrum L, Casagrande A, Peck R B, et al. From Theory to Practice in Soil Mechanics. New York: Wiley, 1960: 43-53.

[2] TERZAGHI K. The shearing resistance of saturated soils [C]// Proceedings of the First International Conference on Soil Mechanics,Cambridge, MA, 1936, 1: 54-56.

[3] SCHOFIELD A, WROTH P. Critical state soil mechanics [M]. New York: McGraw-Hill, 1968.

[4] DARCY H. Les Fontaines Publiques de la Ville de Dijon [M]. Paris: Dalmont, 1856.

[5] MITCHELL J K, SOGA K. Fundamentals of soil behaviour [M]. Hoboken, NJ: John Wiley & Sons, 2005.

[6] SUMMERFIELD M A. Global geomorphology: an introduction to the study of landforms [M]. Harlow: Longman, 1991.

[7] IVERSON R M. The physics of debris flows [J]. Reviews of Geophysics, 1997, 35(3): 245-296.

[8] IVERSON R M. Sensitivity of stability analyses to groundwater data [C]// BELL D H. Proceedings of VIth International Symposium on Landslides, Christchurch, New Zealand. Amsterdam: Balkema, 1991: 451-457.

[9] SASSA K. The mechanism of debris flows [C]// Proc 11th International Conference on Soil Mechanics and Foundation Engineering, San Francisco, 1985, 3: 1173-1176.

[10] WANG G H, SASSA K, FUKUOKA H, et al. Study on the excess pore pressure generation in laboratory-Induced-landslides [C]//Proc 8th Cong Int Assoc Engng Geol and the Environ, Vancouver, 1998, 6: 4237-4244.

[11] WANG G, SASSA K. Factors affecting rainfall-induced flowslides in laboratory flume tests [J]. Geotechnique, 2001, 51(7): 587-599.

[12] SASSA K, FUKUOKA H, WANG G, et al. Undrained dynamicloading ring-shear apparatus and its application to landslide dynamics [J]. Landslides, 2004, 1(1): 7-19.

[13] SASSA K. Prediction of earthquake induced landslides [C]// Proc 7th Int Symp Landslides, Trondheim. The Netherlands: Balkema, 1996, 1: 115-132.

[14] IVERSON R M, COSTA J E, LAHUSEN R G. Debris-flow Flume at H. J. Andrews Experimental Forest - Oregon. Water Fact Sheet, U.S. Geological Survvey Open-File Report, 92-483 [R]. 1992.

[15] MAJOR J J. Depositional processes in large-scale debris-flow experiments [J]. Journal of Geology, 1997, 105(3): 345-366.

[16] IVERSON R M. The debris-flow rheology myth [M]// CHEN C L, RICKENMANN D. Debris flow Mechanics and Mitigation Conference. Davos: Mills Press, 2003: 303-314.

[17] MCARDELL B W, BARTELT P, KOWALSKI J. Field observations of basal forces and fluid pore pressure in a debris flow [J]. Geophys Res Lett, 2007, 34(7): L07406. doi:10.1029/2006GL029183.

[18] IVERSON R M. Debris-flow mechanics [M]// JAKOBAND M, HUNGR O. Debris-flow hazards and related phenomena. Chichester: Springer, 2005.

[19] FORTERRE Y, POULIQUEN O. Long-surface-wave instability in dense granular flows [J]. Journal of Fluid Mechanics, 2003, 486: 21-50.

[20] IVERSON R M, LAHUSEN R G. Reviewed dynamic pore-pressure fluctuations in rapidly shearing granular materials [J]. Science, 1989, 246(4931): 796-799.

[21] 康志成, 李焯芬, 马蔼乃, 等. 中国泥石流研究[M]. 北京: 科学出版社, 2004.

[22] ZHOU G G D, NG C W W. Dimensional analysis of natural debris flows [J]. Canadian Geotechnical Journal, 2010, 47(7): 719-729.

[23] SAVAGE S B. The mechanics of rapid granular flows [J]. Advances in Applied Mechanics, 1984, 24: 289-366.

Effect of pore water pressure on the triggering and mobilization of landslides

ZHOU Gong-dan
Associate Professor, Key Laboratory of Mountain Hazards and Earth Surface Process, Chinese Academy of Sciences; Institute of Mountain Hazards and Environment, Chinese Academy of Sciences & Ministry of Water Conservancy, Chengdu 610041, China

Landslides (slope failure and debris flow) in nature are composed by masses of solid particles and pore fluids. Pore water pressure plays a key role in the triggering of slope failures and enhancing the mobility of debris flows. In this paper, the concept of pore water pressure and its measurement are demonstrated, and the research work about the development of the pore water pressure and its dissipation are also reviewed.

pore water pressure, slope failure, debris flow

(编辑：沈美芳)

10.3969/j.issn.0253-9608.2014.05.003