双组元统一推进系统气路稳定性分析*
尹文娟,魏延明
(北京控制工程研究所,北京100190)
0 引言
双组元统一推进气路系统作为气体增压系统,其功能是通过对推进剂贮箱的增压使推进剂输送系统输出相应流量的推进剂为发动机提供氧化剂和燃料,因此在工作过程中其稳定性必须符合一定要求才能保证发动机的正常工作.然而实际工作过程中,气路系统总会受到外界和内部一些因素的扰动,例如结构参数和工作参数的变化、环境条件的改变等.如果气路系统不稳定,就会在任何微小的扰动作用下偏离原来的平衡状态,并随时间的推移而发散.目前,一般通过数学仿真和试验的方法来分析气路系统的动态特性[1-4],而很少对气路系统的稳定性(抗干扰性)进行理论研究.传统的稳定性研究模型通常是基于对理想气体状态方程进行求导并采用等熵过程假设推导得到;文献[5]针对某膜片式减压阀的稳定性进行了研究,但没有对阻尼腔和卸荷腔建模;文献[6-7]对单独的减压阀稳定性进行了详细研究,但并没有涉及气路系统各个组件间的耦合作用.
本文在双组元推进气路系统的数学模型以及减压阀状态空间模型的基础上[6]进行拓展,采用线性化分析方法,分别建立了气路系统组件的状态空间模型,得到考虑各个组件间耦合的气路系统以及减压阀传递函数模型,探讨了主要结构参数对于气路系统以及减压阀稳定性的影响规律.最后,提出了改善减压阀和气路系统稳定性的主要措施.
1 气路系统简介
气路系统的组成见图1.双组元推进系统气路结构复杂,包含减压器、单向阀、气瓶、贮箱、管路连接件等部件.增压系统工作过程为:手动阀门打开后,气瓶内的高压气体经过减压阀减压,之后分为两路经过单向阀,分别为氧化剂贮箱和燃料贮箱增压.

图1 气路系统原理图Fig.1 Gas system schematic
单向阀主要用于防止推进剂蒸汽逆向进入气路系统而造成故障,其结构原理见图2.当单向阀上、下游压力差大于开启压差时阀芯打开,气体从大、小阀芯与相应阀座之间的缝隙及止回孔流向下游;当上、下游压力差小于开启压差时,阀芯运动件上所受的开启力小于弹簧对阀芯的闭合力,阀芯关闭.

图2 单向阀原理图Fig.2 Check valve(CV)schematic
2 数学模型
文献[6]给出了减压阀的动态数学模型,单向阀的动态数学模型与减压阀类似.同时,考虑到气瓶输出压力为恒定值的工况,贮箱可以简化成一个气腔及气体入口端口和一个液腔及液体出口端口组成的组合件,两个容腔之间的隔膜看成是理想的几何隔离面,两侧压强相等.具体的数学公式不再赘述.
3 状态空间模型
倘若考虑理想气体,且不考虑环境温度的影响,小扰动条件下,稳态点附近的各个腔室温度变化很小,因此这里忽略温度变化带来的影响.采用小偏差法对动态方程进行线性化处理,得到气路系统在稳定点附近的线性化状态空间方程.
3.1 减压阀状态空间模型
文献[6]给出考虑减压阀下游流量为恒值的状态空间模型,而在实际工作过程中,减压阀下游流量和出口压力输出存在一种调节关系.考虑减压阀下游流量对减压阀出口压力输出的影响,假设减压阀出口压力等于单向阀入口压力,下游流量为两路单向阀入口流量之和,得到减压阀状态空间模型为:输入变量:U1=[p1p7],输出变量:Y1=[p2],状态变量:X1=[hhdp2p3p4]T,

式中,系统矩阵A1,输入与输出矩阵B1C1分别为



式中,p1、p2、p3、p4分别为减压阀高压腔、低压腔、反馈腔及卸荷腔压力,p7为单向阀开启腔压力,T2、T3、T4分别为减压阀低压腔、反馈腔及卸荷腔温度,V2、V3、V4分别为减压阀低压腔、反馈腔及卸荷腔容积,Qm1、Qm3、Qm4分别为减压阀阀芯节流处、反馈孔处、卸荷孔处流量,Qm5为单向阀入口流入流量,R为气体常数,h、hd、m分别为减压阀阀芯运动组件位移、速度、质量,Am为膜片有效面积,A2、A4、A1-A0分别为减压阀低压气体、卸荷腔气体以及高压气体作用在阀芯的有效面积,k、c分别为减压阀弹性元件刚度,阻尼系数,dc3为反馈腔直径,dc4为顶杆直径,dc5为卸荷腔直径.(*)0代表参数*在气路系统稳定工作状态时的值.
3.2 传递函数模型
根据气路系统各个组件的关系,得到气路传递函数框图如图3.
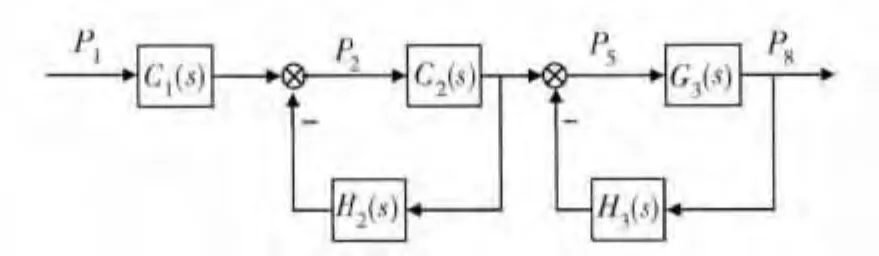
图3 气路系统传递函数框图Fig.3 Transfer function of gas system
图中,P5、P8分别为单向阀出口压力和贮箱气体部分压力,G1(s)为减压阀的执行元件传递函数,G2(s)为单向阀的执行元件传递函数,G3(s)为贮箱的执行元件传递函数,H2(s)为单向阀对于减压阀出口的反馈回路传递函数,H3(s)为贮箱对于单向阀出口的反馈回路传递函数.
根据图3,可以分别得到从减压阀入口到贮箱出口的气路系统闭环传递函数以及带有单向阀压力、流量反馈回路的减压阀闭环传递函数.
4 动态响应过程仿真与分析
考虑减压阀入口压力为恒定值的工况,对气路系统从启动到额定工况的工作过程进行动态响应特性仿真.其中,工作介质为氦气,减压阀入口压力为12 MPa,系统温度为 293.15 K.仿真中,在第 6 s,两路贮箱下游阀门打开,在第12 s,下游阀门关闭.
从图4的减压阀、单向阀、贮箱气体部分的压力仿真曲线可以看出,在理想气体绝热流动的假设下,气路系统的仿真曲线虽然在关闭阶段和试验曲线有所差异,没有由传热引起的压力升高再下降现象,但是对气路系统在稳态时刻的动态特性影响并不大.

图4 气路系统动态特性曲线Fig.4 Characteristics of gas system
由图4所示的温度变化可以看出,各腔室温度虽然在下游阀门开启之后一段时间里变化剧烈,但变化幅度并不大.因此,在稳态工作过程,各个腔室的气流状态变化可近似为等温过程.
5 动态稳定性分析
一般,减压阀的反馈孔直径、弹簧阻尼系数、出口腔容积、阀芯运动组件质量以及单向阀止回孔直径对气路稳定性影响很大.因此,分别分析这几个参数对气路稳定性的影响,同时,以主导闭环极点距离虚轴的距离作为稳定性程度的判断依据.
5.1 减压阀结构参数对气路稳定性的影响
图5为各个减压阀相关结构参数对于气路稳定性的影响规律示意图.可以看出,使得气路系统和减压阀稳定的减压阀反馈孔直径参数范围是一致的.但在相同结构参数下,气路系统的稳定性程度却优于减压阀.事实上,在工作参数恒定,气体流动均匀、绝热的情况下,系统稳定性范围主要由阀门的阀芯运动规律决定.由于单向阀在稳态工作点附近,大小阀芯的开度基本不会发生变化,因此,即使增加了单向阀和贮箱两个组件,各个结构参数对于气路系统和减压阀的稳定性影响规律在范围上是一致的.虽然单向阀和贮箱对气路系统的稳定性范围基本不造成影响,却使得气路系统在各个结构参数下的闭环主导极点距虚轴的距离存在一个极值,因此,在存在扰动的情况下,收敛速度大范围慢于减压阀.
改善减压阀和气路系统稳定性主要有两个途径:适当降低阀芯运动的灵敏度以及减缓反馈腔压力对于阀芯运动的反馈.图5(a)和图5(b)分别表示不同反馈孔直径和不同减压阀下游管路容积对减压阀以及气路系统稳定性的影响.可以看出,减小减压阀反馈孔直径和增大减压阀下游管路容积都可以减缓减压阀反馈腔压力对于阀芯运动的反馈,提高减压阀和气路系统的稳定性.同时,若减压阀反馈孔直径过小或者减压阀下游管路容积过大则会使得减压阀反馈腔的压力变化延迟过大,稳定性变差.如图5(c)和图5(d)所示,减小减压阀阀芯运动组件质量和增大减压阀弹簧阻尼系数则是通过降低阀芯运动的灵敏度来提高减压阀以及气路系统的稳定性.
5.2 单向阀结构参数对气路稳定性的影响
图6以减压阀反馈孔直径为例,研究了不同单向阀止回孔直径对于减压阀和气路系统稳定性的影响规律.
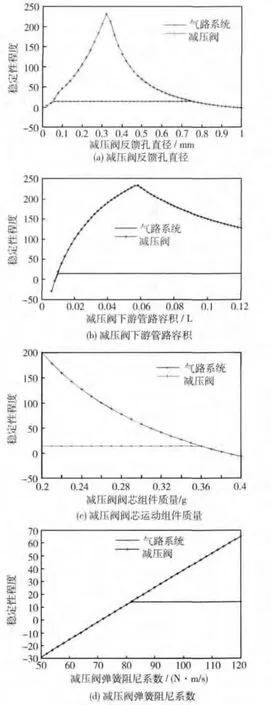
图5 减压阀结构参数对稳定性的影响Fig.5 Influences of PRV's structure parameters on the stability
由于不同的单向阀止回孔直径不仅会影响下游的稳态输出,而且也会影响到其上游减压阀的稳态工作点,因此,从图6看到,不同单向阀止回孔直径对应着不同的气路稳定性影响规律曲线.单向阀止回孔直径越小,额定流量下的单向阀开启腔和止回腔之前的压差越大,施加给粘连在一起的大、小阀芯的力也就越大,单向阀阀芯开度越稳定,气路系统似乎越不容易产生振荡.然而,从抗干扰性的角度来看,止回孔直径的减小并不会影响使得减压阀和气路系统稳定的结构参数范围.并且止回孔直径越小,减压阀和气路系统的最大闭环主导极点距虚轴的距离反而大范围减小,收敛速度变慢,稳定性变差.
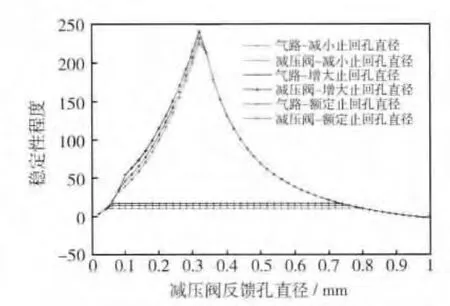
图6 单向阀结构参数对稳定性的影响Fig.6 Influences of CV's structure parameters on the stability
6 结论
本文针对以往文献对双组元统一推进气路系统抗干扰性理论研究方面的不足,在文献[6]基础上进行拓展,建立了考虑组件耦合的气路系统闭环传递函数模型,探讨了结构参数对于气路系统稳定性的影响规律,从中得到以下结论:
(1)在工作参数恒定,气体流动均匀、绝热的情况下,系统的稳定性范围主要由阀门的阀芯运动规律决定.因此,即使增加了单向阀和贮箱两个组件,各个结构参数对于气路系统和减压阀的稳定性影响规律在范围上是一致的.
(2)虽然单向阀和贮箱对气路系统的稳定性范围基本上不造成影响,却使得气路系统在各个结构参数下的闭环主导极点距虚轴的距离存在极限值,使得其收敛速度大范围慢于减压阀.
(3)适当减小反馈孔直径、增大减压阀下游管路容积、减小减压阀阀芯运动组件质量以及增大减压阀弹簧阻尼系数都可以同时提高减压阀和气路系统的稳定性.
(4)单向阀止回孔直径越小,单向阀阀芯开度越稳定,但是,减压阀和气路系统的最大闭环主导极点距虚轴的距离反而大范围减小,收敛速度变慢,稳定性变差,因而对单向阀止回孔直径的选择要进行综合考虑.
[1]HURLBERT E,ABE J T.Methods used to investigate and resolve the space shuttle helium pressure regulator instability[C]//The 26thAIAA /ASME/SAE/ASEE Joint Propulsion Conference.Orlando:AIAA,1990:11-17.
[2]SEKITA R,MATSUDA M,NAKAMURA R.Pressure oscillation analyses of the pressure regulator for the HIIA propulsion system [C].The 26thAIAA/ASME/SAE/ASEE Joint Propulsion Conference.Alabama:AIAA,2003:1-9.
[3]陈晓琴.减压阀充填过程动态特性仿真[J].导弹与航天运载技术,2006(5):48-52.Chen X Q.Dynamic simulation of the pressure reducing valve in filling conditions[J].Journal of Missile and Space Vehicle,2006(5):48-52.
[4]张雪梅,张黎辉,金广明,等.减压器动态过程的数学仿真[J].航空动力学报,2004,19(4):110-114.ZHANG X M,ZHANG L H,JIN G M.Numerical simulation of the dynamic process for pressure regulator[J].Journal of Aerospace Power,2004,19(4):110-114.
[5]尤裕荣,曾维亮.气体减压阀的稳定性分析[J].火箭推进,2009(10):34-38.YOU Y R,ZENG W L.Analysis on pneumatic pressure reducing valve stablity[J].Journal of Rocket Propulsion,2009(10):34-38.
[6]尹文娟,魏延明.减压阀动态响应特性与稳定性研究[J].空间控制技术与应用,2013,39(3):24-29.YIN W J,WEI Y M.Analysis on responding characteristics and stability of pneumatic pressure reducing valve[J].Aerospace Control and Application,2013,39(3):24-29.
[7]NACI Z,GREG R L.Stability of gas pressure regulators[J].Applied Mathematical Modeling,2008(32):61-82.

