SPSS回归分析法构建灵江临海洪峰水位的预报模型
叶凌云
(台州市水文站 浙江台州 318000)
引言
感潮河段是河流与海洋的过渡段,在该河段上,一方面有来自上游径流的影响,另一方面又受到下游潮汐的作用,是受径流和潮流共同作用的河段。由于两种水流的共同作用,加上河口区本身的一些地理特性,使感潮河段的水文情势较河流和海洋复杂,并具有独自的特点,由于问题的复杂,目前较常用的预报方法仍主要是经验相关法和回归分析法。
社会科学统计软件 SPSS(以下简称 SPSS)是世界上最早的统计分析软件,目前已经广泛应用于众多领域和行业。在国际学术交流中,凡使用 SPSS软件完成的计算,可以不必说明算法,可见影响之大。作为统计分析工具,SPSS软件理论严谨、内容丰富,数据管理、统计分析、趋势研究、制表绘图、文字处理等功能,几乎无所不包。本文应用 SPSS软件对感潮河段控制站临海站进行预报,把临海站上游多个站点的水位、雨量作为影响因子,进行回归分析,建立预报模型。
1 流域情况
灵江流域地处浙江省东南沿海,位于120°~130°E、28°30′~29°30′N间,是浙江八大水系之一。它北以天台山为界,南有括苍山,其间山丘起伏,植被一般,属亚热带季风性气候区。夏秋季节,不仅常受台风影响,出现较大暴雨洪水,而且常受东风波等天气系统的影响,产生较强降雨。临海站是灵江流域控制站,集雨面积4356km2,距椒江河口57km,潮汐影响显著。当上游洪水下泄时,潮汐影响随洪水位的升高而减弱,当临海站洪水位高于 8m时, 水位过程线中潮形基本消失,潮汐影响基本消失。上游干流永安溪源于天堂尖,穿越仙居县,入临海市西部,河长141.3km , 集雨面积约2702km2;临海站上游5km,有最大支流始丰溪汇入,始丰溪源于大盘山东麗,穿越天台县,河长134.2km ,集雨面积约1610km2。 灵江流域水文站网密度较大,站点较多,观测资料系列比较长,采用回归分析法可以综合各种因素,建立预报模型,可以在感潮河段的水位预报中取得较好的效果。
2 数据和分析11
2.1 变量引入
临海站河段是典型的感潮河段,导致洪水发生的因素较多,并且复杂多变。由于近二十年来流域特性发生较大变化,本文主要收集了 1980年到 2012年流域洪水资料,根据临海站实际情况,共引入自变量10个,因变量1个。10个自变量指的是:仙居站洪峰水位1H、仙居洪峰水位发生时(t时刻)的沙段站同时水位2H ,t时刻天台站同时水位3H ,t时刻柏枝岙站4H ,t时刻临海站同时水位5H ,t时刻以前 6小时流域平均降雨量1P,t时刻以前6小时百步站、柏枝岙站、临海站区间降雨量2P,t时刻以前 12小时流域平均降雨量3P, t时刻以前12小时百步站、柏枝岙站、临海站区间降雨量4P,t时刻仙居站和临海站水位差6H 。因变量是临海站洪峰水位H。
2.2 分析方法
SPSS软件可以进行数据管理、统计分析、图表分析和输出管理,可为水文预报提供崭新的操作环境平台和丰富的技术方法。本文主要在临海站上游仙居站洪峰水位出现时,对临海站的洪峰水位进行预报,预见期 10个小时左右,分析步骤如下:
(1)打开SPSS数据文件窗口,建立由因变量(临海站洪峰水位)和10个自变量组成的SPSS数据文件并保存。按照“分析→描述性统计”对所有的因变量和自变量进行描述性统计,为分析的数据提供一个直观的描述。
(2)在数据编辑窗口中进行包含分类自变量的多元线性逐步回归分析。按照“分析→回归→线性”操作步骤计算预报对象的估计值;按照“转换→计算变量”操作步骤生成临海洪峰水位实测值与估计值之间的相对拟合误差。SPSS软件会把这些计算数据和结果自动保存在数据编辑窗口中。然后按照“图形→旧对话框→线图”操作步骤生成临海洪峰水位实测值与其估计值组成的历史拟合曲线,SPSS软件会自动在数据编辑窗口中保存数据和计算结果,并在输出窗口中输出剔除因子和引人因子的统计结果、相关信息、图形等。
(3)对回归效果进行检验。SPSS软件会自动进行回归效果的统计检验,包括回归方程的拟合度检验、回归方程的显著性检验和回归系数的显著性检验。拟合度检验通常用复相关系数 R2来判断,R2越接近于 1,表明回归直线的拟合程度越好;回归方程的显著性检验(F检验)和回归系数的显著性检验(t检验)都是计算样本统计量的相伴概率P值,将其与给定的显著水平α(即信度)值相比较。若P<α,则表明在这一信度水平上,回归方程的回归系数有统计学意义;若P>α,则表明在这一信度水平上,回归方程的回归系数无统计学意义。
(4)若通过统计检验,则可用包含分类自变量的多元线性回归方程对临海洪峰水位进行预报,也可进行概率区间预报。当因变量Y服从正态分布时,对应i个预报因子的观测值 xi的预报对象估计值 yi落在区间[yi-Sy,yi+Sy]内的可能性约为68%,落在区间[yi-2Sy,yi+2Sy]内的可能性约为95%(Sy为剩余标准差),Sy越小,用回归方程所估计的值就越精确。
3 回归性分析
3.1 拟合度检验
由表 1可以看出,回归模型的相关系数R=0.991,复相关系数R2=0.982,R2接近于1,表明回归直线的拟合度高。修正的相关系数为0.974,估计值的标准误差为0.212,标准误差较小,表示用回归方程估算的预报值相对精度较高。根据德宾—瓦特逊检验其自相关度,系数接近于 2,表示基本没有自相关关系,对预报的结果不会使预报结果失去有效性。由此可见,本次回归方程的拟合度较好。

表1 模型汇总

表2 方差分析
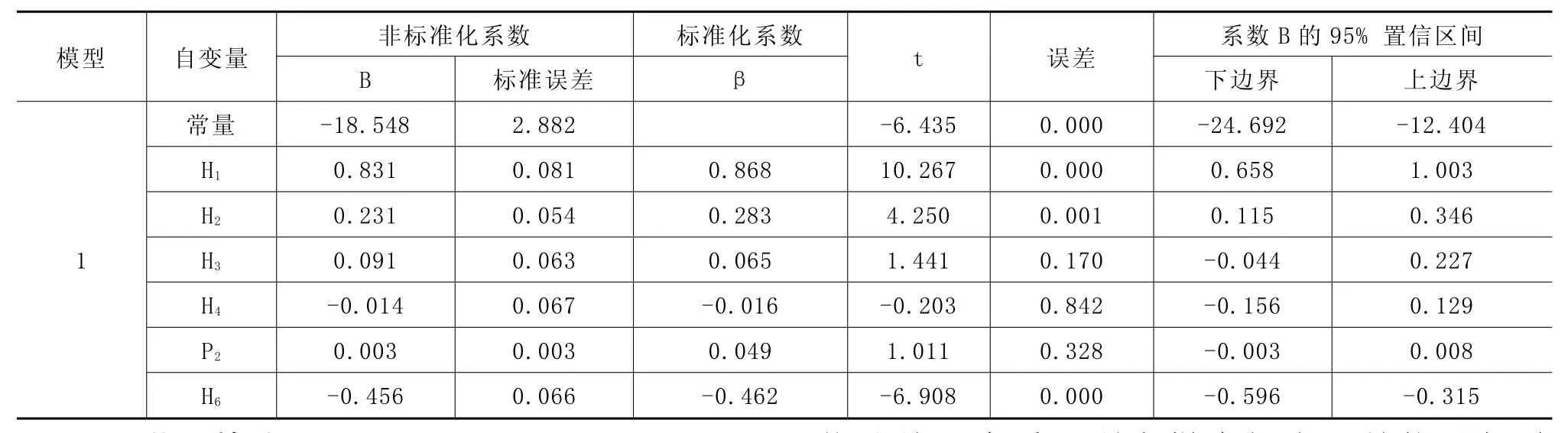
表3 预报模型系数
3.2 显著性检验
由表 2可以看出:回归模型的回归平方和35.77,均方差为5.932;剩余平方和为0.673,均方差 0.045。统计量 F=132.831,相伴概率值为ρ=0.000<0.001(信度),说明回归方程通过了显著性检验,预报值和因子之间有线性关系。
3.3 预报模型
由表3中可以看出,有部分自变量从预报模型中剔除,这就说明这些自变量与临海洪峰水位不存在显著的线性关系,不将其引入回归方程。剩余自变量都通过了回归系数的显著性检验(t检验),说明具有回归意义,不能从回归方程中剔除。由此可见,通过多元线性回归可以找出预报值和哪种影响因子的整体相关度高,并且剔除相关度低的影响因子,从而降低样本数据的冗余度。从图1中可以看出残差具有正态分布,从而可以认为得出的多元线性回归方程是合理的,可表示为:
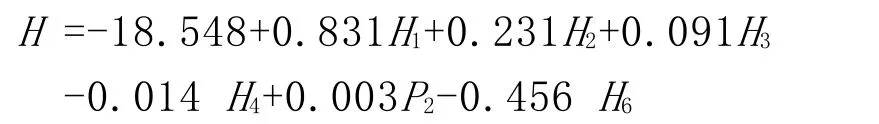
3.4 结果分析
从1980年到2012年的发生洪水时临海洪峰水位实测值和预报值的拟合曲线(见图2)可以看到,曲线拟合结果较好。根据SPSS 的统计计算结果显示临海洪峰水位的平均值为8.81m,标准差 1.305,实测临海洪峰水位的平均值为8.81m,两者差值为0,预报精度高。从所选样本统计结果来看,所有样本拟合误差均不超过0.30m,相对误差均小于3%。根据《水文情报预报规范》(GB/T 22482—2008)临海站水位预报允许误差为0.50m,样本预报合格率100%。表4中列出了从2000年到2012年临海站几场大洪水的洪峰水位预报结果。
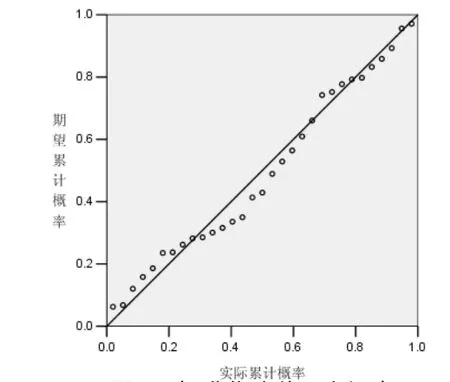
图1 标准化残差正态概率
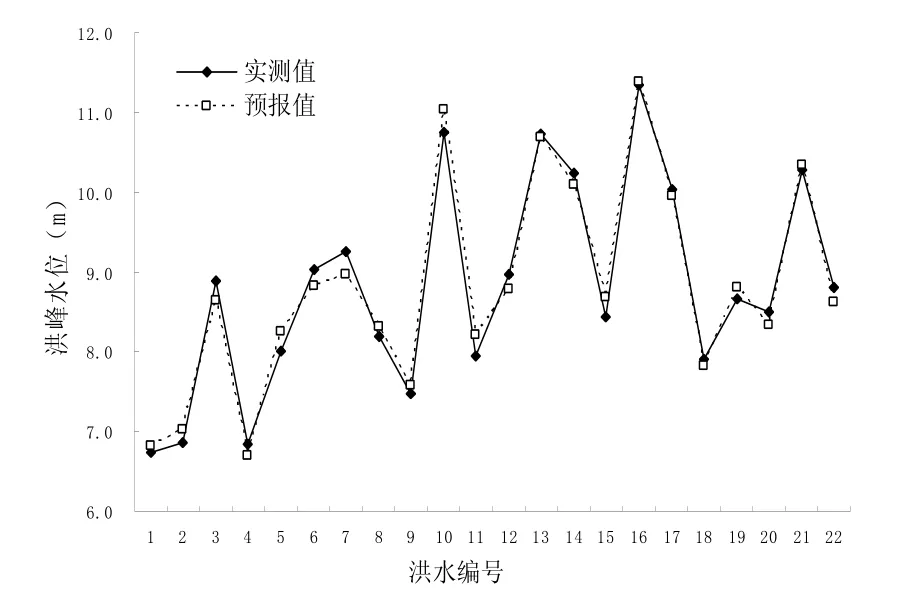
图2 临海站洪峰水位实测值和预报值拟合曲线
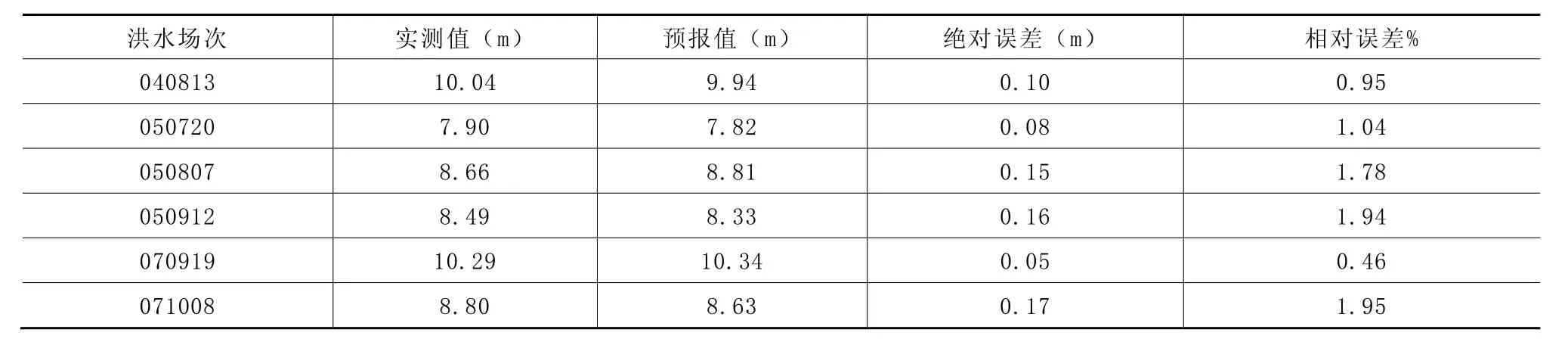
表4 2000-2012年临海几场大洪水的洪峰水位预报结果
4 结论
(1)SPSS作为统计软件,简单易操作,具有强大的统计分析功能,特别在受到多重影响因素影响的感潮河段,可以利用现有资料,迅速的建立有关方程。
(2)从建立的预报方程来看,剔除了部分因子,根据临海站实际情况,当临海站上游洪水下泄时,潮汐影响随洪水位的升高而减弱,当临海站洪水位高于 8m时, 水位过程线中潮形基本消失,潮汐影响基本消失。本文洪水都选择几十年来较大的洪水,洪水水位均超过或者接近8m,因此剔除预报时临海水位是合理的。但当水位不足8m时,潮汐影响较大,6m以下时,潮汐主要控制临海站水位,当临海站处于高潮位时候,对临海洪峰水位预报值影响较大。另外一方面,暴雨中心的位置及其走向也是影响洪水位的因素之一,需进一步研究和考虑。
1. 刘曾美,吴俊校,陈子燊.感潮地区暴雨和潮水位遭遇组合的涝灾风险[J].武汉大学学报(工学版2010,43(2)),167-168
2. 杨竞,童祯恭,刘玉哲.SPSS软件对饮用水质进行主成分分析评价的运用[J].环境科学与技术,2011,34(7)171-174.
3. 陈斌,包为民,瞿思敏,元晓华.双向线性回归模型在椒江临海站水位预报中的应用[J].水文,2008,28(3):45-48.
4. 王姝,柴建设.基于社会科学统计(SPSS)回归性分析的尾矿库事故预测模型[J].中国安全科学学报,2008,18(12):35-39.
5. 胡广录,张济世,樊立娟.基于SPSS软件的黑河正义峡下泄水量预报分析[J].人民黄河,2013,35(4)22-28.

