基于误差放大因子的多基地声纳定位误差分析

李大龙，杨日杰，韩建辉

（海军航空工程学院，山东　烟台　264001）

基于误差放大因子的多基地声纳定位误差分析

李大龙，杨日杰，韩建辉

（海军航空工程学院，山东烟台264001）

摘要：研究了多基地声纳定位中的椭圆交叉定位与双曲线交叉定位方法，由公式推导分析了输入误差对两种定位结果的影响，给出了误差放大因子的定义，通过计算机仿真，比较了不同站位分置距离下，误差放大因子的变化情况。同时，在相同阵型配置下，对比了椭圆交叉定位与双曲线交叉定位的优劣。结果表明，增大多基地各站址的分置距离，可以扩大具有较好定位精度的区域。

关键词：基地声纳；椭圆交叉定位；双曲线交叉定位；定位误差；误差放大因子

0　引言

多基地探潜系统的工作机制是：发射机发出信号，由多个接收机（如浮标）接收潜艇目标反射的回波信号［1～3]。目标的位置信息可以由一些交叉定位的方法得到［4]。这种定位方法是建立在浮标探测到目标基础上，根据浮标信号/回波的波达时间数据和方位数据进行定位。由于声纳浮标的位置误差，目标方位误差和测量时间误差等输入误差的存在，使得每次测量得到的目标位置是不精确的［5]。为了使探测的信息有利用价值，定位误差必须要足够的小。

本文研究了多基地定位误差与声纳浮标位置误差、方位误差和时间误差的关系，其主要目的是为了减小声纳浮标的定位误差，提高探测定位的精度。

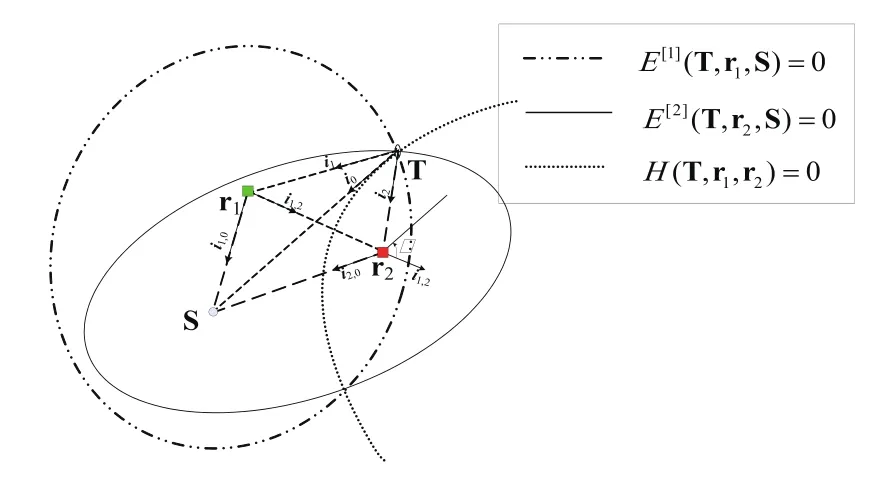
图1　椭圆交叉定位与双曲线交叉定位示意图Fig.1 The schematic diagram of el l iptic and hyperbol ic cross fixes

1　交叉定位原理

假设在一个多基地系统中，由一个主动声纳作为发射器和两个被动声纳浮标作为接收器，位置如图1所示，分别为S、r1和r2，目标的位置为T。

假设声速c已知且为常数，声线建模为直线，每个接收机能够记录从发射机发出的信号直达波波达时间和从目标反射回来的回波波达时间，于是得到下列时间差：

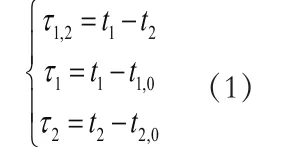
其中，tk代表回波到达第k个接收器的时间，tk，0代表直达波到达第k个接收器的时间。为第一个接收器与第二个接收器记录回波的时间差，为第k个接收器记录回波与记录直达波的时间差。

由式（1）中的时间差可以得到目标位置曲线方程：

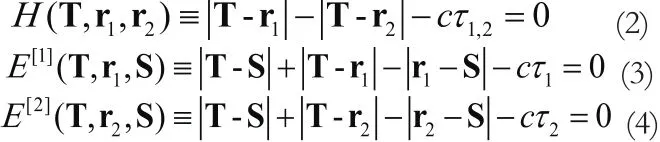
式（2）定义了一条双曲线，其焦点为r1和r2；式（3）和（4）定义了两个椭圆，其中一个椭圆的焦点为S和r1，另一个椭圆的焦点为S和r2。

联立式（3）和式（4），得：

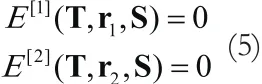
通过式（5）完成定位的方法称为椭圆交叉定位法。

将式（2）与式（3）或式（4）联立，得：

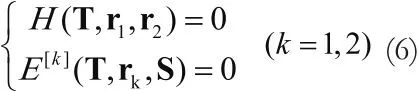
通过式（6）完成定位的方法称为双曲线定位。

2　输入误差对交叉定位的影响

假设浮标位置存在误差，用S+dS，r1+dr1，r2+dr2代替浮标的真实位置r1，r2，S，则求解出来的目标估计位置T+dT应满足：

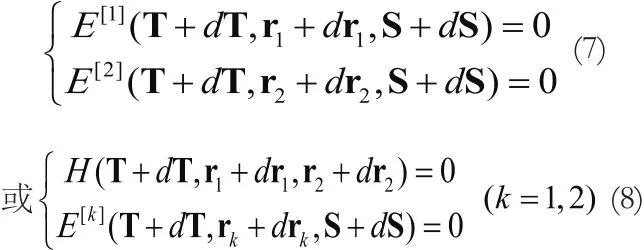
定义：

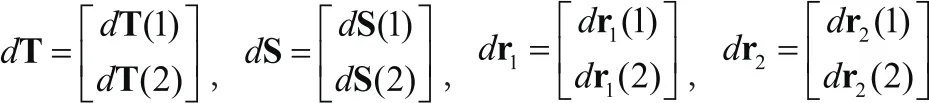
2.1椭圆交叉定位中的输入误差分析

在第一个线性近似系统中，式（7）等价于：其中

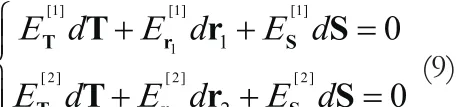
采用0m×n表示m×n的零矩阵，可以将式（9）写成矩阵形式有：

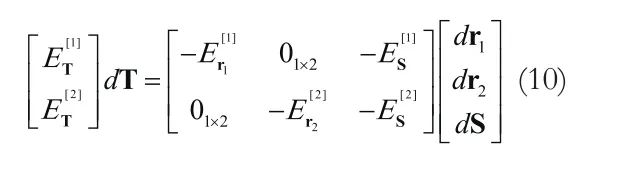
定义三个矩阵：

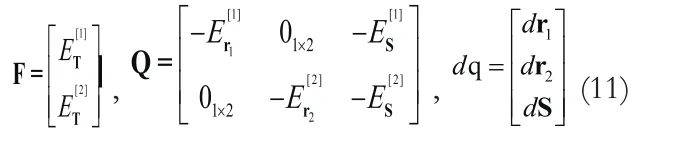
若F-1存在，则式（10）可以写为dT=F-1Qdq，且有：

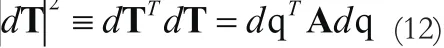
其中A=QT（FFT）-1Q，为对称矩阵，其本征值为λk（k=1，…，6）。取相似变换矩阵M使得：

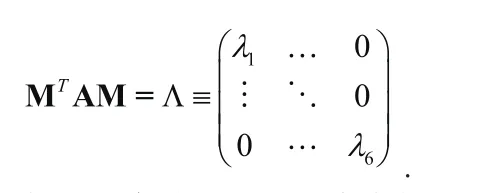
设构成矩阵M的标准正交特征向量是有序的.定义误差放大因子［6，7]为：

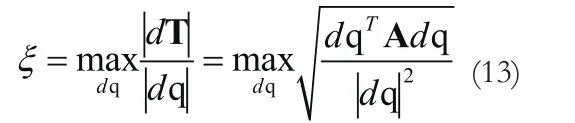
由上式可知：

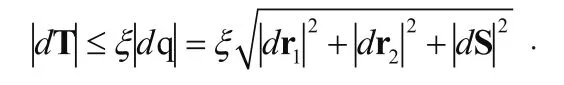
其中，误差放大因子ξ是由dS，dr1和dr2共同作用的，若式（7）中的dS和dr2为02×1，经过计算就可以得到第一个接收器的误差放大因子ξ1。同理可得第二个接收器和发射器对应的误差放大因子ξ2和ξ0。

引入向量dξ使得dq=Mdξ，代入式（13）得：

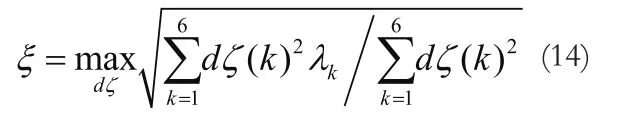
2.2双曲线交叉定位中的输入误差分析

与双椭圆交叉定位分析方法相似，有如下矩阵等式：

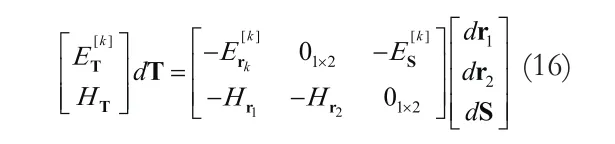
其中：

关于误差放大因子ξ和λmax，与双椭圆交叉定位有相同的形式。

3　仿真分析

对误差放大因子ξ进行数值分析需要下列方程：

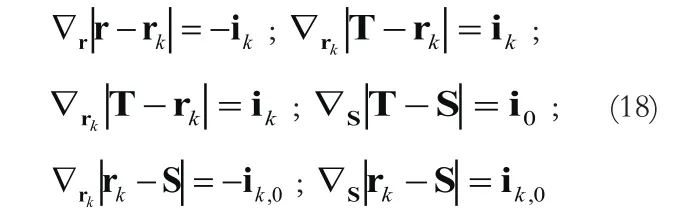
联立式（2）、（3）、（4）和（18）可得：

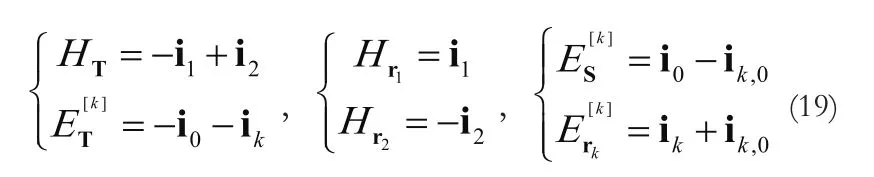
将式（19）代入式（11）和式（17）定义的矩阵F与Q.

仿真采用两种参数进行比较：

条件1：发射站坐标S=（0，0）km，两个接收站坐标分别为r1=（-7，0）km，r2=（0，-7）km；

条件2：发射站坐标S=（0，0）km，两个接收站坐标分别为r1=（-19，0）km，r2=（0，-19）km。

3.1椭圆交叉定位的误差放大因子仿真联立式（11）与式（19），得：

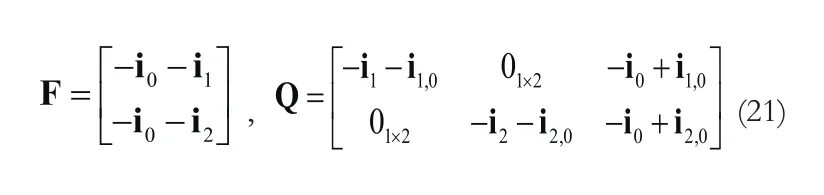
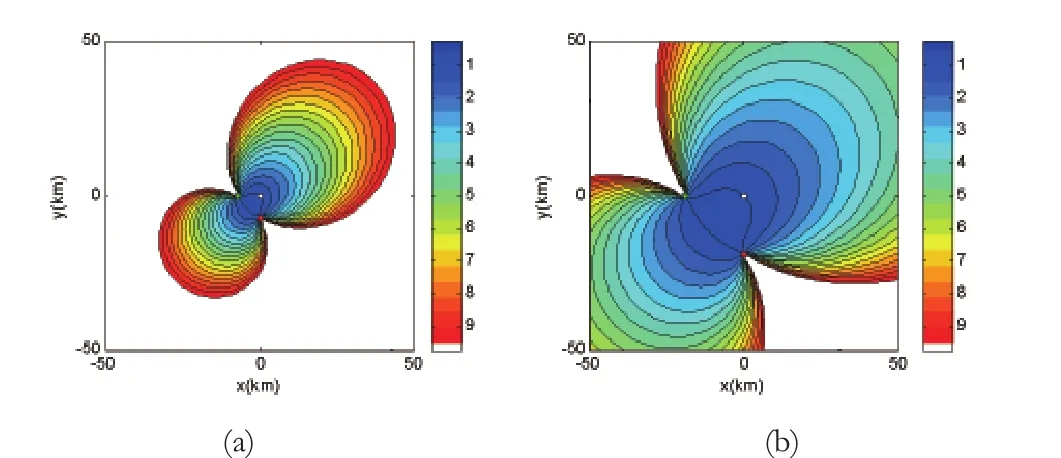
图2　椭圆交叉定位方法中的误差放大因子Fig.2 The er ror magni fication factor in the el l iptic cross fix

图2中圆圈代表发射站坐标位置，两个方块代表接收站坐标位置，绿色方块为r1位置，红色方块为r2位置。（a）为条件1的仿真结果；（b）为条件2的仿真结果。由图2可以看出，相同配置阵型下，站位间不同分置距离所引起的误差放大因子分布形状一致，但取值相同的覆盖范围不同。具体地说，对于给定的多基地浮标阵型，增大多基地各站址的分置距离，可以扩大具有较小误差放大因子的区域。

3.2双曲线交叉定位的误差放大因子仿真

联立式（17）与式（19）可得，当k=1时，有：

当k=2时，有：

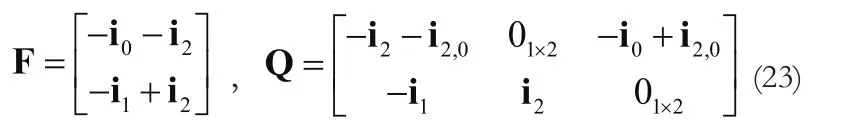
图3中的（a）与（b）都是在条件2下得到的仿真结果。从图中可以看出，在相同的阵型配置，多基地各站址的分置距离相同的情况下，（a）与（b）中的两类双曲线交叉定位在基线附近存在“盲区”，这个区域内的误差放大因子数值很大，定位性能较差。再将图3与图2（b）作比较可以看到，在相同的阵型配置，多基地各站址的分置距离相同的情况下，椭圆交叉定位的误差放大因子较小的区域要比双曲线交叉定位的区域大。

4　结论

本文从椭圆交叉定位和双曲线交叉定位的公式出发，分析和推导了输入误差对两种类型定位的影响，给出基于误差放大因子分析定位性能的方法。通过仿真表明，对于给定的多基地浮标阵型，增大多基地各站址的分置距离，可以扩大具有较小误差放大因子的区域。并且通过对比发现，椭圆交叉定位要优于双曲线交叉定位。

参考文献：

［1]H.Cox..Underwater acoustic data processing［M]，Kluwer，1989：3～24.

［2］J.Bowen and R.Mi tnick，A mul t istat ic per formance predict ion methodology［J].Johns Hopkins APL Technical Digest，1999，20（3）：424¯431.

［3]S.Coraluppi，Mul tistatic sonar local ization［J]，IEEE J.Ocean.Eng.，2006，31（4）：964～974.

［4]L.Mozzone and P.Lorenze l l i，Target Loca l izat ion wi th Mul tiple Sonar Receivers［R]，SACLANTCEN Repor t，SR-

317，1999.10

［5］M.McIntyre，et al.The ef fect of position uncer tainty in mul tistatic acoustic local isation［C]，In：Proc.Conf.Inf.Decision Control， Aust ral ia，1999：347～352.

［6]M.Sandys-Wunsch and M.G.Hazen，Mul tistatic local ization er ror due to receiver positioning er rors［J］，IEEE J.Ocean.Eng.，2002，27（2）：328～334.

［7]Se r g e y Sima k o v，Lo c a l i z a t i o n i n Ai r bo r ne Mu l t i s t a t i c Sona r s［J]，IEEE J.Ocean.Eng.，2008，33（3）：278～288.

Analysis of the Mu ltistatic Sonar Positioning Errors Based on Error Magnification Factor

LI Da-long，YANG Ri-jie，HAN Jian-hui
（Naval Aeronau tical Eng ineering Institu te，Yan tai 264001，China）

Abstract：The elliptic and hyperbolic cross f xes in the multistatic sonar localization method is studied.By the formula derivation，the effect of input errors on the two positioning results is analyzed.We proposed the def nition of the error magnif cation factor，and compared the variety of error magnif cation factor for the same pattern conf guration but different separation distances by the simulation.Also the performance of the cross f xes between elliptic and hyperbolic is researched.The results indicate that the area where the error magnif cation factor is small can be enlarged by increasing the separation distance.

Key words：multistatic sonar；elliptic cross f x；hyperbolic cross f x；positioning error；error magnif cation factor