Diagnosis of Physical and Biological Controls on Phytoplankton Distribution in the Sargasso Sea
WANG Caixia, and Paola Malanotte-Rizzoli
1) Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, P. R. China
2) Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Diagnosis of Physical and Biological Controls on Phytoplankton Distribution in the Sargasso Sea
WANG Caixia1),*, and Paola Malanotte-Rizzoli2)
1) Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, P. R. China
2) Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
The linkage between physical and biological processes is studied by applying a one-dimensional physical-biological coupled model to the Sargasso Sea. The physical model is the Princeton Ocean Model and the biological model is a five-component system including phytoplankton, zooplankton, nitrate, ammonium, and detritus. The coupling between the physical and biological model is accomplished through vertical mixing which is parameterized by the level 2.5 Mellor and Yamada turbulence closure scheme. The coupled model investigates the annual cycle of ecosystem production and the response to external forcing, such as heat flux, wind stress, and surface salinity, and the relative importance of physical processes in affecting the ecosystem. Sensitivity experiments are also carried out, which provide information on how the model bio-chemical parameters affect the biological system. The computed seasonal cycles compare reasonably well with the observations of the Bermuda Atlantic Time-series Study (BATS). The spring bloom of phytoplankton occurs in March and April, right after the weakening of the winter mixing and before the establishment of the summer stratification. The bloom of zooplankton occurs about two weeks after the bloom of phytoplankton. The sensitivity experiments show that zooplankton is more sensitive to the variations of biochemical parameters than phytoplankton.
physical-biological coupled model; annual cycle; external forcing; bio-chemical parameter
1 Introduction
Photosynthesis, the conversion of solar energy to chemical energy, is a fundamental step in which inorganic carbon is fixed by algae and converted into primary production. Significant primary production can only occur in the well-lit euphotic zone. Hence, the animals which feed on the primary production can survive mostly within the mixed layer where a large quantity of food is available. Physical processes play an important role in marine ecosystem dynamics (Collinset al., 2009; Denman and Pena, 2002; Mann and Lazier, 1991) and can modify or limit biological production through the nutrient supply and mean irradiance field (e.g., McClainet al., 1990; Mitchellet al., 1991). This paper studies the linkage between physical and biological processes in the Sargasso Sea via the application of a physical-biological coupled model. The model is one-dimensional and designed to investigate the vertical structure of the upper ocean mixed layer. The depth of the mixed layer, the intensity of solar radiation penetrating into water column, and the vertical distribution of dissolved nutrients are some of the major factors regulating the biosystem of the sea. The seasonal variation in the atmosphere-ocean heat flux imparts a seasonal cycle to the depth of the mixed layer (Menzel and Ryther, 1960). The variation of wind stress also affects the depth of the mixed layer. According to Menzel and Ryther (1960), production off Bermuda in the Sargasso Sea is closely related to vertical mixing, high levels occurring when the water is well mixed to or near the permanent thermocline at 400 m depth and low levels when a seasonal thermocline is present in the upper 100 m.
Ecosystem models have been widely applied to different oceanic conditions (e.g., Varelaet al., 1992; Radach and Moll, 1993; Sharples and Tett, 1994). A recent application of a similar coupled physical-biological model using the BATS data (Doneyet al., 1996) well reproduced the seasonal cycles of the upper water column temperature field, as well as of the chlorophyll and primary production.
The goals of this study are to investigate and understand the interplaying and relative importance of the physical processes and the vertical distributions of nutrients and biomass in the euphotic zone. The biochemical part comprises five components,i.e., nitrate, ammonium, phytoplankton, zooplankton, and detritus (Oguzet al., 1996). A case-study is carried out by applying the model to the Sargasso Sea oligotrophic region, using the site data from the U. S. Joint Global Ocean Flux Study (JGOFS) Ber-muda Atlantic Time-series Study (BATS). The coupling between the biological and physical model is accomplished via vertical mixing coefficients. The study begins with examining the seasonal response of the mixed layer physics and biology to external forcing, including windstress, heat flux, and surface salinity. Following that, sensitivity experiments of the model components to biochemical parameters are performed in order to understand how the internal biochemical parameters affect and what the impact of nutrients, light availability, and the interaction between the biochemicals and production is on the biological system.
2 The Method
The complete model includes the physical and biological submodels, which is one-dimensional and time-dependent. The vertical mixing process is parameterized by the level 2.5 Mellor and Yamada turbulence closure scheme (Mellor and Yamada, 1982). The biological submodel is intentionally kept simple to explore the basic biological interactions and mechanisms.
2.1 The Physical Model
The physical model is the one-dimensional version of the Princeton Ocean Model (Blumberg and Mellor, 1987). For a horizontally homogeneous and incompressible sea water body under Boussinesq and hydrostatic approximations, the horizontal momentum equation is expressed as

wheretis time,zis the vertical coordinate,is the horizontal velocity of the mean flow with the components (u,v), ˆkis the unit vector in the vertical direction,fis the Coriolis parameter,Kmdenotes the coefficient for the vertical turbulent diffusion of momentum, andvmrepresents its background value associated with internal wave mixing and other small-scale mixing processes.
The temperatureTand salinityScan be determined from the transport equation,

whereCdenotes eitherTorS,Khis the coefficient for the vertical turbulent diffusion, andvhis its background value. For simplicity, the solar irradiance which penetrates into the water column is not parameterized in the temperature equation. It is represented through the surface boundary condition together with other heat flux components. The density is a function of potential temperature, salinity, and pressure, written as a non-linear equation of state,ρ=ρ(T,S,p) (Mellor, 1990).
The vertical mixing coefficients are determined from

wherelandqare the turbulent length scale and turbulent velocity, respectively.SmandShare the stability factors as in Mellor and Yamada (1982). In the level 2.5 turbulence closure,landqare computed from the turbulent kinetic energy,q2/2, and the turbulent macroscale equations. The turbulent buoyancy and shear productions are calculated by the vertical shear of horizontal velocity and vertical density gradient of the mean flow.Khis the eddy coefficient for the vertical turbulent diffusion of biological variables.
The boundary conditions at the sea surfacez=0 are


whereCagain denotes eitherTorS.
2.2 The Biological Model
Nitrogen plays a critical role in ocean biology as an important limiting nutrient, particularly in subtropical gyres, and is a natural currency for studying biological flows (Fashamet al., 1990). Biological constituents in the coupled model are treated as equivalent concentrations of nitrogen (mmolN m−3).Following the physical rules outlined above the advection and diffusion of biological scalars and the biological interactions are modeled as nitrogen flows between compartments. The investigation in ecosystem modeling focuses on identifying the appropriate types of compartments and the linkages among them.
Detailed models may produce better and more realistic simulation results, but at the expenses of added complexity, less interpretable solutions, and increasing number of free parameters. Therefore, an attempt has been made to keep the model as simple as possible without eliminating essential dynamics of the system. The simple, five- component system including phytoplanktonP, zooplanktonZ, nitrateN, ammoniumA, and detritusDis outlined schematically in Fig.1.
The local changes of biochemical variables are described by

whereBrepresents one of the five biological variables, phytoplankton biomassP, herbivorous zooplankton biomassZ, pelagic detritusD, nitrateN, and ammonium concentrationA.FBis the biological interaction term, which, for the five biological variables, can be written as (e.g., Wroblewski, 1977; Fashamet al., 1990):

where the parameters and their default values are given in Table 1.

Table 1 Parameters and model default values (Wroblewiski et al., 1988; Doney et al., 1996; Hurtt and Armstrong, 1996; Oguz et al., 1996)
The total production of phytoplankton, Φ(I,N,A), is defined by

wherea(I) andβt(N,A)represent the light limitation and the total nitrogen limitation function of phytoplankton uptake, respectively. The empirical relationship between the maximum phytoplankton growth rate and temperature was used to assign the maximum phytoplankton growth rateσm(Eppley, 1972; Fashamet al., 1990) andβt(N,A) is given in the form of
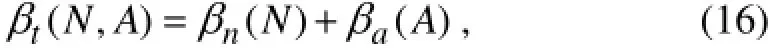
withβa(A) andβn(N) representing the contributions of ammonium and nitrate limitations, respectively. These two terms are expressed by the Michaelis-Menten uptake formulation as
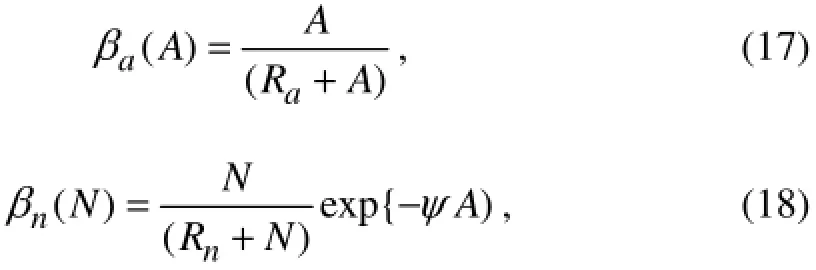
whereRnandRaare the half-saturation constants for nitrate and ammonium, respectively. The exponential term of Eq. (18) represents the inhibiting effect of ammonium concentration on nitrate uptake, withψsignifying the inhibition parameter (Wroblewski, 1977).
The individual contributions of nitrate and ammonium uptakes to the phytoplankton production are represented by (Varelaet al., 1992)
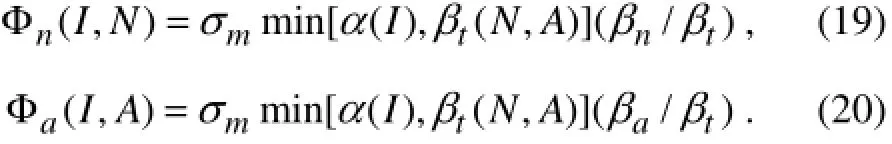
The light limitation is parameterized by Jassby and Platt (1976)

whereais the parameter of photosynthesis efficiency controlling the slope ofα(I) to the irradiance curve at low values of the photosynthetically active irradiance (PAR).Isdenotes the surface intensity of PAR, which is taken as 0.45 for the climatological incoming solar radiation according to the available data.
The zooplankton grazing ability is represented by the Michaelis-Menten formulation

For phytoplankton, zooplankton, nitrate, and ammonium, the boundary conditions at the surface and bottom are given by

For the detritus equation the surface boundary condition is modified to include the downward sinking flux
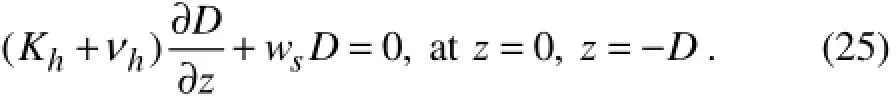
The same condition is also prescribed at the lower boundary of the model, which is well below the euphotic zone at 400 m depth. A relatively low sinking rate is specified (ws=0.5 m d−1, Table 1). The advantage of selecting the bottom boundary at a considerable distance away from the euphotic layer is to allow the complete remineralization of detrital material before reaching the lower boundary of the model. The vertically integrated biological model is fully conservative.
2.3 Physical Forcing
The annual variations of wind stress and heat flux components are expressed by smoothed and climatological surface forcing functions (Doneyet al., 1996)

where the time,t, is given in days. The annual mean, seasonal amplitude, and phase, as shown in Table 2, are computed from climatological data sets (Esbensen and Kushnir, 1981; Isemer and Hasse, 1985) for the region of the BATS site (31˚50΄N and 64˚10΄W). According to Zhuet al.(2002), the estimated non-solar heat fluxes at a high time resolution could have large errors even if observation errors are small, but with a lower time resolution the large errors could be avoided.

Table 2 Climatological physical forcing functions for the default case
The surface wind stress (Fig.2c) peaks at 1.2 dyn cm−2in March, and the annual mean heat loss from the nonsolar terms is 248.5 W m−2with a maximum of 365.5 W m−2in late December. Solar radiation is computed with a constant cloud fraction of 0.75, which leads to an annual mean solar heating rate of 198.7 W m−2that is within the reported climatological range of 180–200 W m−2(Esbensen and Knshnir, 1981). The required cloud fraction, however, is slightly higher than the climatological value of approximately 0.6 near Bermuda (Warrenet al., 1988). The annual heat budget at Bermuda is not closed locally by air-sea exchange (the dashed line in Fig.2a), therefore, an excess heat flux at the surface is added in our model in order to run stable, multi-year integrations. The surface heat flux function we used to force the model is the solid line in Fig.2a.
Surface salinity was derived using linear interpolation of monthly mean CTD data at the top 8 meter of water column (World Ocean Atlas Levitus94). As shown in Fig.2b, salinity reaches the maximum value of 36.7 during winter and early spring, and the minimum value of 36.4 during summer. The variations in PAR (Fig.2d) were the climatological data from the World Ocean Atlas (Levitus94). The PAR is expressed as a harmonic function with an amplitude of 30 W m−2and centered at 70 W m−2on February 28.
Temperature and salinity profiles are initialized with the Levitus94 September data as shown in Figs.3a and 3b, respectively. Biological simulations are initialized with a uniform nitrate concentration of 0.3 mmolN m−3in the mixed layer (0–150 m), increasing linearly below that layer to 6.0 mmolN m−3at 400 m (Fig.3c).
The model equations are solved using the finite difference procedure described by Mellor (1990). There are a total of 27 vertical layers for the 400 m of water column and the grid resolution increases toward the surface. An implicit scheme is used to avoid computational instabilities associated with small grid spacing and a time step of 10 min in numerical integration. The Aselin filter is applied at every time step to avoid time splitting due to the leapfrog scheme. The detailed solution steps are as follows: 1) The physical model is integrated for 5 years. An annual steady state cycle is reached after 3 years of integration. 2) The biological model is coupled with the fifth year solution of the physical model and integrated for 4years, at the end of which the annual cycle of biological variables is obtained. The depth integrated total nitrogen content over the annual cycle,Nt=N+A+P+Z+D, should remain a constant if the equilibrium state is reached.

Fig.2 Annual variations in model surface boundary conditions. a) surface heat flux (solid line) and annual heat budget (dashed line) at Bermuda; b) salinity; c) wind stress; d) photosynthetic available irradiance.
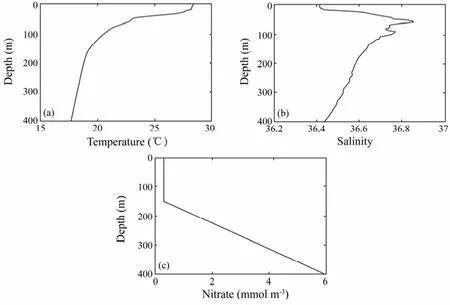
Fig.3 Model initial conditions of a) temperature; b) salinity; c) nitrate.
3 Results
3.1 Response of Upper Layer Physical Structure to Physical Forcing
The annual response of the upper layer physical structure to physical forcing functions is shown in Fig.4. The winter structure is characterized by strong cooling and mixed layer deepening. In February and March the mixed layer depth can exceed 220 m with a mixed layer temperature of about 19.5℃ and a high eddy diffusivity (Fig.4c). After mid-April, the water column warms up gradually and the mixed layer depth decreases. Due to weak mixing, weak wind, and strong heating in summer, water surface temperature increases up to a maximum value of 27℃, the mixed layer shoals to a less than 10 m depth, and a sharp thermocline at the base of the mixed layer is developed. The characteristics of wind-related and shallow mixed layer are consistent with low values of eddy diffusivity shown in Fig.4c. The autumn period is characterized by a mixed layer depth of 50–75 m and temperature around 22℃, salinity around 36.575, which is followed by a deeper penetration of the mixed layer and cold water mass formation as a result of strong cooling in winter (January and February).

Fig.4 The time and depth variations in a) temperature, b) salinity, and c) eddy diffusion coefficient.
3.2 Response of the Upper Layer Biological Structure to Physical Forcing
The temporal and vertical distributions of five biochemical variables are shown in Fig.5. There are several phases of the biological structure within a year, agreeing with the physical structure of the upper ocean. Due to the deep convection in winter, the surface layer is rich with nutrients entrained from below. The mixed layer nitrogen concentration increases gradually to its maxima in April. As a result of nutrient enrichment and sufficient light availability, the phytoplankton bloom begins to develop in January and reaches the maximum level in March and April. During the same period, the water column is overturned completely and the deepest and coolest mixed layer is established due to strong vertical mixing. The spring phytoplankton grow during March and April until June. The summer and fall periods are characterized by nutrient depletion and low phytoplankton production in the mixed layer. The phytoplankton biomass is low because, with weak convection, the nutrient supply from the nutrient-rich water below the mixed layer is no longer available and the phytoplankton biomass is consumed by herbivore in surface waters. In summer, the stratification and the strong seasonal thermocline inhibit nutrient flux into the shallow mixed layer from below, and therefore prohibit the development of bloom during summer. Nitrate concentrations below the thermocline increase and, together with sufficient light availability, lead to the surface maximum of phytoplankton biomass in the layer between the seasonal thermocline and the base of the euphotic zone during July and August. Remineralization of particulate organic material following degradation of the spring bloom produces ammonium. Part of the ammonium is used in regenerated production and the rest is converted to nitrate through the nitrification process. The yearly distributions of zooplankton and detritus closely follow that of phytoplankton with a time lag of approximately two weeks. The maximum zooplankton concentrations correspond to phytoplankton blooms in spring as well as subsurface phytoplankton maximum in summer.
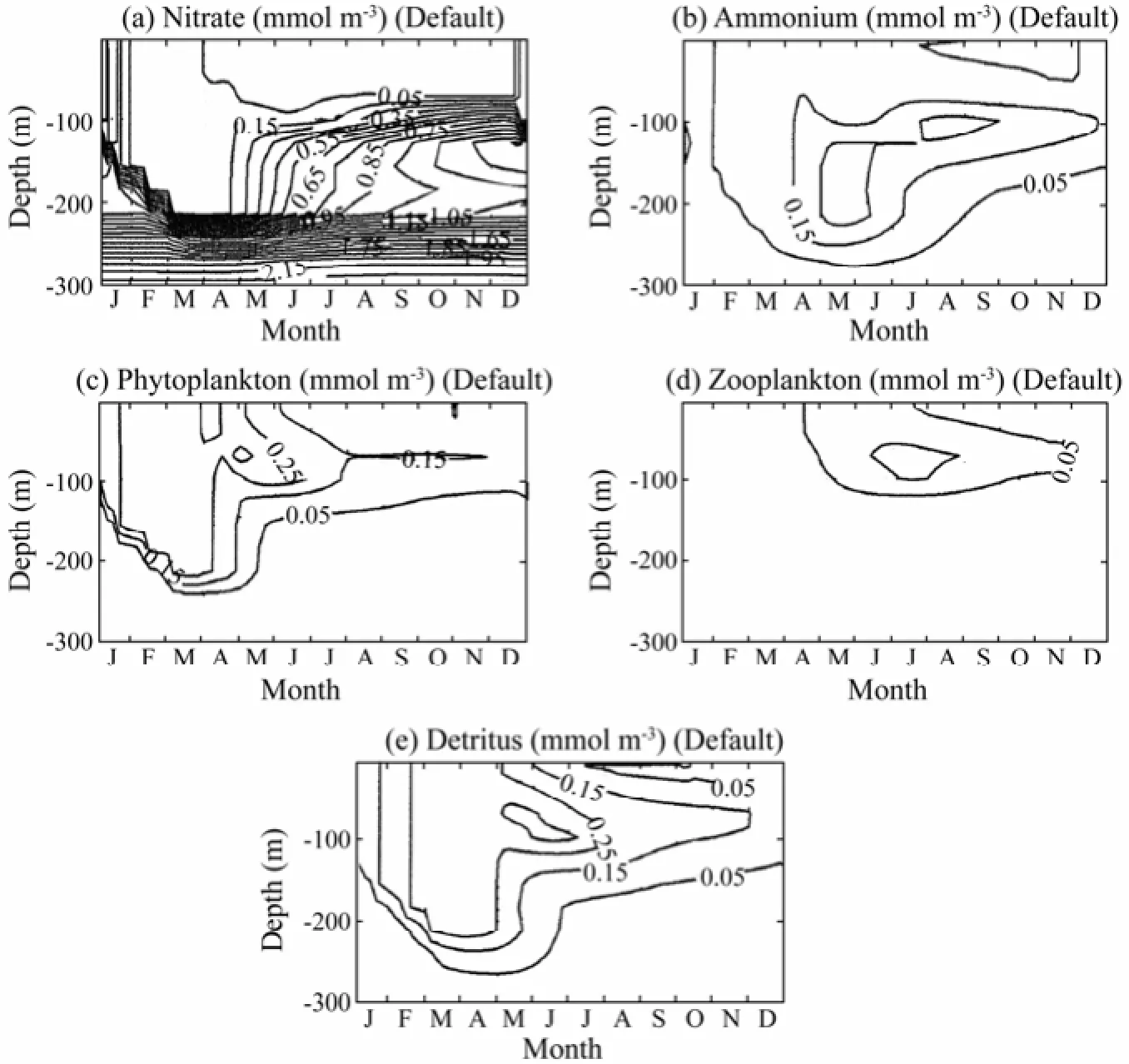
Fig.5 The time and depth variations in (a) nitrate, (b) ammonium, (c) phytoplankton, (d) zooplankton, and (e) detritus.
3.3 Dynamics of Phytoplankton Blooms
In this section, the main mechanisms controlling the initiation, development and degradation of blooms, as well as the subsurface maximum during summer, are briefly described. First, the relative roles of light and nutrient uptake are considered in the primary production process. The control of phytoplankton growth by either light or nutrient limitation during one year is shown in Figs.6a and 6b. The light limitation function has the opposite structure with values decreasing towards deeper levels (Fig.6a). The relatively high gradient region at about 50–100 m depths separates the low region near the surface from the high nitrogen limitation region below during summer (Fig.6b). Therefore, the net growth function (Fig.6c), which has the minimum of light and nitrogen limitations, is generally governed by nitrogen limitation near the surface and by light limitation at deeper levels. A subsurface maximum is present at depths of about 50–100 m where both light and nitrogen limitations have moderate values. During summer, this is responsible for the subsurface phytoplankton production.

Fig.6 The time and depth variations in a) nondimensional light limitation function, b) nondimensional nutrient limitation function, and c) net limitation function in one year.

Fig.7 The time and depth variations in a) new production, b) regenerated production, c) zooplankton grazing, and d) time change of phytoplankton.
Fig.6c shows that the net growth function has the highest values within the upper 50 m layer during January and February. But the bloom develops around the end of March as shown in Fig.5c. There are two reasons for theabsence of the bloom generation in mid-winter. First, the amount of phytoplankton biomass at that time is not sufficient to initiate the bloom. Secondly, the relatively strong downward diffusion at surface layer (Fig.4c) counteracts against the primary production and therefore prevents the bloom development. However, as soon as the intensity of vertical mixing diminishes in April, a new balance is established. The time variation term of phytoplankton reaches the maximum at the surface at the beginning of April and the subsurface maximum is attained in the second half of April (Fig.7d). This new balance leads to an exponential growth of phytoplankton in the mixed layer. Soon after the initiation phase, zooplankton grazing (Fig.7c) begins to dominate the system and balance the primary production. This continues until nitrate stocks in the mixed layer are depleted and the nitratebased primary production (new production) (Fig.7a) weakens. At the same time, the rapid recycling of particulate material allows for the ammonium-based regenerated production (Fig.7b), and contributes to the bloom development. The bloom terminates abruptly towards the end of May when ammonium stocks are no longer sufficient for the regenerated production.
The downward diffusion process in the mixed layer is evident withKhvalues of greater than 2 cm2s−1from January to April (Fig.4c). The termination of convective mixing process in late April is indicated in Fig.4c by a sudden decrease ofKh. As shown further in Figs.4a and 5c, the period of highKhvalues is identified with vertically uniform temperature structure of about 19.5℃ and the phytoplankton structure of approximately 0.3 mmolN m−3. Following the termination of convective overturning, the subsurface stratification begins to establish. As the mixed layer temperature increases by about 0.5℃ from 19.5℃to 20℃, the phytoplankton bloom reaches its peak amplitude of 3.5 mmolN m−3within half month.
4 Comparison of Model Results with BATS Observations
The calculated temperature and salinity (Fig.4) compare well with the climatological data (1961–1970) (Fig.8) from Hydrostation S (WHOI and BBSR, 1988; Musgraveet al., 1988) and with the model results of Doneyet al. (1996). The results clearly reproduce the deep winter convective depth, shallow summer mixed layer, and sharp seasonal thermocline found in the data. The seasonal salinity cycle also generally agrees with climatology, showing the peak salinity during the winter convection period and the formation of a fresh surface layer during summer. A sub-surface salinity maximumS>36.6 appears in both the calculated results and the observations.
The biological model is driven with a uniform nitrate concentration of 0.3 mmolN m−3in the mixed layer (0–150 m), increasing linearly below the mixed layer to 6.0 mmolN m−3at the 400 m depth. A direct comparison between the coupled model and the data is difficult because the BATS dataset shows significant interannual variability and its available record is relatively short for generating a true biological climatology. The climatological forcing has a likely effect on the model results of reduced variability in deep convection during winter, causing homogenization of properties through the winter mixed layer depth, and weakening individual bloom events driven by short-term variability. Monthly nitrate climatologies for the first four years of BATS (1988–1992) are shown in Fig.9 (Knapet al., 1991, 1992, 1993). The climatologies are useful for revealing the general characteristics of the model results, but quantitative comparisons should be limited to more robust features of biological seasonal cycle. The calculated nitrate field agrees reasonably well with the BATS data. Winter surface con-centrations are about 0.2 mmolN m−3and the summer nitracline depth is at about 100–125 m depths. The approximately uniform concentration in the deep winter mixed layer gradually increases through summer due to the remineralization of detritus. However, the calculated nitrate values are generally lower than the observed.

Fig.8 Climatological (1961–1970) seasonal cycles of a) temperature and b) salinity at Hydrostation S (WHOI and BBSR, 1988; Musgrave et al., 1988; Doney et al., 1996).

Fig.9 Climatological seasonal cycle of nitrate for the first 4 years (1988–1992) of the BATS record (unit: mmol m−3) (Knap et al., 1991, 1992, 1993).
5 Sensitivity Studies
A series of experiments are carried out to analyze the model sensitivity to some adjustable parameters (Table 1). The experiments and the parameter values for each experiment are listed in Table 3. The experiments show that if one parameter affects phytoplankton distribution, it will have more influence on zooplankton. The important parameters that affect the structure of phytoplankton, and therefore that of zooplankton, are the maximum phytoplankton growth rateσm, the phytoplankton death ratemp, the light extinction coefficientkw, the nitrate half-saturation constantRn, the maximum herbivore grazing raterg, the herbivore death ratemh, the herbivore excretion rateμh, the herbivore assimilation efficiencyγh, the herbivore half-saturation constantRg, the detrital remineralization rateε, and the detrital sinking ratews. The bloom structure is not sensitive to the phytoplankton self-shading coefficientkc, the ammonium half-saturation constantRa, the photosynthesis efficiency parametera, and the ammonium oxidation rate. Three examples are presented below to examine how the biological parameters affect phytoplankton and zooplankton.
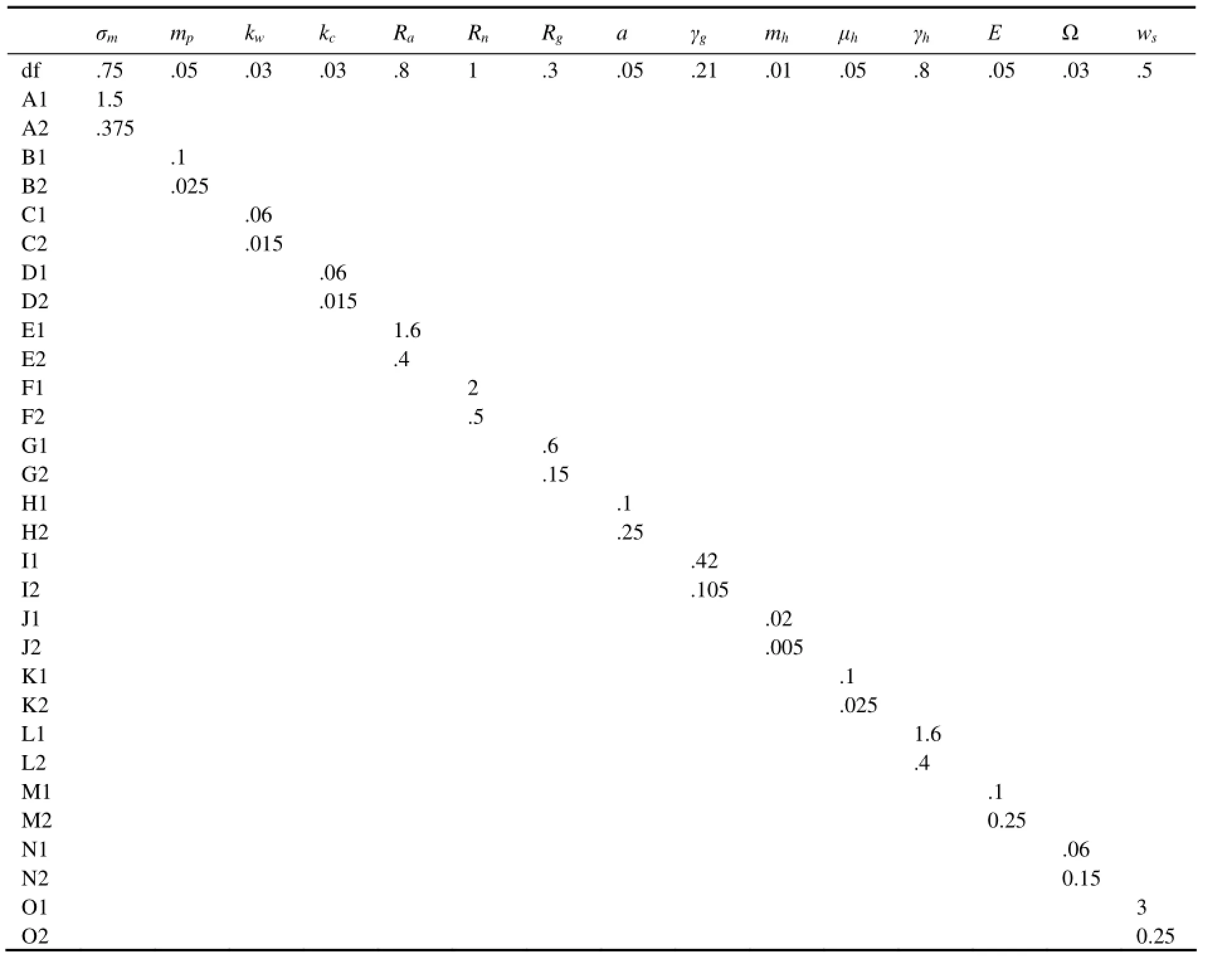
Table 3 Parameters for sensitivity experiments (‘df’ stands for the default value. The default is used if no value is shown in a box)
5.1 Sensitivity to the Extinction Coefficient of PAR Value (Defaultkw=0.03 m−1)
As shown in Table 3, two experiments were carried out with the PAR extinction coefficient ofkw=0.06 m−1andkw=0.015 m−1in experiments C1 and C2, respectively. Increasing the defaultkwvalue intensifies the distribution of phytoplankton and zooplankton towards the sea surface (Figs.10c and 10d). Decreasing its value, the distributions of phytoplankton and zooplankton are stretched into deeper water (Figs.11c and 11d). In the model, the phytoplankton growth rate depends on the minimum of nutrient limitation and light limitation. It is governed by the nitrogen limitation near the surface and by the light limitation at deeper levels. Comparing the light limitation in Fig.10a with Fig.6a, it can be seen that the light limitation in experiment Cl decreases in the entire water column except for the very near surface. The most striking difference is that in the default case, the 0.05 contour of light limitation is located between 100 and 150 m depths, while it is between 66 and 84 m in experiment Cl. The subsurface maxima of net limitation decreases and shifts to-wards the sea surface except in winter, which corresponds to the squeezing of the phytoplankton distribution towards the sea surface. The zooplankton, which feeds on phytoplankton, also moves about 50 m closer to the sea surface than in the default case. The dynamics in experiment C2 is opposite to that in experiment Cl.
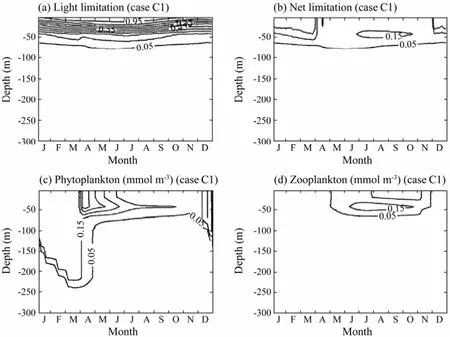
Fig.10 The time and depth variations in Expriment Cl of a) the light limitation function, b) the net limitation function, c) phytoplankton, and d) zooplankton in one year.

Fig.11 The time and depth variations in Expriment C2 of a) the light limitation function, b) the net limitation function, c) phytoplankton, and d) zooplankton in one year.
5.2 Sensitivity to the Nitrate Half Saturation Coefficient (DefaultRn=1 mmolN m−3)
If algae are placed in a nutrient medium, the concentration of nutrients decreases over time in the medium as they are incorporated into plant cells. The nutrient uptake rate of algae depends on nutrient concentration in the medium (Valiela, 1995). The nitrate or ammonium uptake rate of phytoplankton has a hyperbolic relationship with the nitrate or ammonium concentration in the environ-ment (Eppleyet al., 1969). In the Michaelis-Menten equation, the half saturation constant reflects the relative ability of phytoplankton in using nutrients of low levels and thus may be of ecological significance. In the case of nitrate, nutrient uptake occurs in two steps. First, nutrients are taken into a phytoplankton cell at a rate determined by ambient nutrient concentration. Then, as the concentration inside the cell increases, nutrient is utilized in proportion to internal cellular concentration. If the nitrate uptake rate is measured when ammonium is present, the uptake of nitrate maybe greatly underestimated because of the preference for ammonium by different algae. The half saturation constant is high in more euphotic and nutrient-rich waters, but is low in oligotrophic waters.
Two experiments were carried out withRn=2 mmolN m−3andRn=0.5 mmolN m−3in experiments Fl and F2, respectively. IncreasingRnin expriment Fl increases the strength and duration of the phytoplankton spring bloom (Figs.12a and 12b). The subsurface maximum of phytoplankton now extends into July, while in the default case it extends into June. However, zooplankton has only weak distribution that spans the period from July to November in the upper 120 m. Opposite results were obtained when the value ofRnwas decreased in case F2 (Figs.12c and 12d). The subsurface maximum of phytoplankton now only extends into May while the distribution of zooplankton is much stronger than in experiment F1, spanning the period form March to November.

Fig.12 The time and depth variations of a) phytoplankton and b) zooplankton in case Fl; c) phytoplankton and d) zooplankton in case F2.
5.3 Sensitivity to the Detrital Sinking Rate (Defaultws=0.5 m d−1)
The sinking rate of particulate organic matter,ws, is one of the most critical parameters in the model. The appropriate value ofwsfor the model is 0.5 m d−1, which implies that the faster sinking and larger particles do not contribute to the processes taking place within the euphotic zone. Greater sinking values of detrital material decrease the detritus and subsequently nitrogen concentrations in the euphotic layer. Figs.13a and 13b show the results with the sinking rate of 3 m d−1, and Figs.13c and 13d 0.025 m d−1. The change inwsalters the whole biological system drastically. In case O1,ws=3 m d−1, and there exists only a weak bloom in April and May (Fig.13a), with almost no zooplankton biomass and detritus in the study area. The euphotic layer is depleted of both ammonium and nitrate accumulated at deeper levels. The case withws=0.025 m d−1allows a more than complete remineralization of detrital material before it reaches the lower boundary of the model. The concentrations of phytoplankton and zooplankton are higher with the decrease ofws, than in the default case as shown in Figs.13c and 13d, especially during winter when the complete water column overturning provides rich supplies of nutrients in the euphotic zone.
6 Conclusions
In this paper, the interaction between physical and biological dynamics in the Sargasso Sea is studied. The response of a five-component ecosystem to the external forcing, including heat flux, wind, and salinity, and sensitivities of the ecosystem to biochemical parameters are investigated.

Fig.13 The time and depth variations of a) phytoplankton and b) zooplankton in case O1; c) phytoplankton and d) zooplankton in case O2.
The model results compare quite successfully with the observations and the calculated results by Doneyet al.(1996). The base simulation and the sensitivity experiments show a seasonal cycle of physics and biology. In summer, the shallow seasonal thermocline depth and the weak convection inhibit nutrient supplies from the mixed layer below, therefore the concentrations of all biochemical variables are low and limited to a thin surface layer. In winter, the strong vertical mixing and convection bring more nutrients to the euphotic zone. Hence, in March and April, right after winter, phytoplankton feeding upon nutrients reaches its spring bloom level. The bloom of zooplankton, which feeds on phytoplankton, follows the bloom of phytoplankton with a time lag of about two weeks. The results of the sensitivity experiments show that zooplankton is generally more sensitive to the variation of biochemical parameters than phytoplankton. The system is sensitive to all the parameters except the phytoplankton self-shading coefficient, the ammonium half-saturation constant, the photosynthesis efficiency parameter, and the ammonium oxidation rate. For example, a smaller detrital sinking rate and a higher detrital remineralization rate provide higher nutrient concentration in the euphotic zone, while a smaller light extinction coefficient corresponds to stronger and deeper penetrating solar radiation in water column. Both circumstances create a more intense bloom, deeper in space and lasting longer in time.
Acknowledgements
We thank Prof. Temel Oguz at the Institute of Marine Sciences, Middle East Technical University, Turkey, and Prof. Xianqing Lv at Ocean University of China for helpful discussions. This work was supported by the Shandong Young Scientists Research Awards under grant BS2011HZ021.
Blumberg, A. F., and Mellor, G. L., 1987. A description of a three-dimensional coastal ocean circulation model. In: Three Dimensional Coastal Ocean Models. Heaps, N. S., ed., American Geophysical Union, Washington, DC, 1-16.
Collins, A. K., Allen, S. E., and Pawlowicz, R., 2009. The role of wind in determining the timing of the spring bloom in the Strait of Georgia. Canadian Journal of Fisheries and Aquatic Sciences, 66 (9): 1597-1616.
Denman, K. L., and Pena, M. A., 2002. The response of two coupled one-dimensional mixed layer/planktonic ecosystem models to climate change in the NE subarctic Pacific Ocean. Deep-Sea Research II, 49 (24-25): 5739-5757, DOI: 10.1016/ S0967-0645(02)00212-6.
Doney, S. C., Glover, D. M., and Najjar, R. G., 1996. A new coupled, one-dimensional biological-physical model for the upper ocean: Applications to the JGOFS Bermuda Atlantic Time Series (BATS) Site. Deep-Sea Research II, 43 (2-3): 591-624.
Eppley, R. W., Rogers, J. N., and McCarthy, J., 1969. Halfsaturation constant for uptake of nitrate and ammonium by marine phytoplankton. Limnology and Oceanography, 14: 912-920.
Eppley, R. W., 1972. Temperature and phytoplankton growth in the sea. Fishery Bulletin, 70: 1063-1085.
Esbensen, S. K., and Kushnir, Y., 1981. The heat budget of the global ocean: An atlas based on estimates from surface marine observations. Climatic Research Institute, Report 29, Oregon State University, USA.
Fasham, M. J. R., Ducklow, H. W., and McKelvie, S. M., 1990. A nitrogen-based model of plankton dynamics in the oceanic mixed layer. Journal of Marine Research, 48: 591-639.
Hurtt, G. C., and Armstrong, R. A., 1996. A pelagic ecosystem model calibrated with BATS data. Deep-Sea Research II, 43: 653-683.
Isemer, H., and Hasse, L., 1985. The Bunker Climate Atlas of the North Atlantic Ocean: Volume 2: Air-Sea Interactions. Springer-Verlag, New York, 252pp.
Jassby, A. D., and Platt, T., 1976. Mathematical formulation of the relationship between photosynthesis and light for phytopankton. Limnology and Oceanography, 21: 540-547.
Knap, A. H., Michaels, A. F., Dow, R. L., Johnson, R. J., Gundersen, K., Sorensen, J. C., Close, A. R., Hammer, M., Bates, N., Knauer, G. A., Lohrenz, S. E., Asper, V. A., Thel, M., Duddow, H., and Quinby, H., 1993. Data Report for BATS 25-BATS 36, October 1990–September 1991. U. S. JGOFS Bermuda Atlantic Time-series Study, U. S. JGOFS Planning Office, Woods Hole, MA, 339pp.
Knap, A. H., Michaels, A. F., Dow, R. L., Johnson, R. J., Gundersen, K., Sorensen, J. C., Close, A. R., Hammer, M., Knauer, G. A., Lohrenz, S. E., Asper, V. A., Thel, M., Duddow, H., Quinby, H., Brewer, P., and Bidigare, R., 1992. Data Report for BATS 13-BATS 24, October 1989–September 1990. U. S. JGOFS Bermuda Atlantic Time-series Study, U. S. JGOFS Planning Office, Woods Hole, MA, 345pp.
Knap, A. H., Michaels, A. F., Dow, R. L., Johnson, R. J., Gundersen, K., Knauer, C. A., Lohrenz, S. E., Asper, V. A., Tuel, M., Duddow, H., Quinby, H., and Brewer, P., 1991. Data Report for BATS 1-BATS 12, October 1988–September 1989. U. S. JGOFS Bermuda Atlantic Time-series Study, U. S. JGOFS Planning Office, Woods Hole, MA, 286pp.
Mann, K. H., and Lazier, J. R. N., 1991. Dynamics of Marine Ecosystem Biological-Physical Interaction in the Oceans. Blackwell Scientific Publications, 466pp.
Mellor, G. L., 1990. User’s Guide for a Three Dimensional, Primitive Equation Numerical Ocean Model. Princeton University, Princeton, NJ, 35pp.
Mellor, G. L., and Yamada, T., 1982. Development of a turbulence closure model for geophysical fluid problems. Reviews of Geophysics and Space Physics, 20 (4): 851-875.
McClain, C. R., Esaias, W. E., Feldman, G. C., Elrod, J., Endres, D., Fireston, J., Darzi, M., Evans, R., and Brown, J., 1990. Physical and biological processes in the North Atlantic during the first GARP global experiment. Journal of Geophysical Research, 95: 18027-18048.
Menzel, D. W., and Ryther, J. H., 1960. The annual cycle of primary production in the Sargasso Sea off Bermuda. Deep-Sea Research, 6: 351-367.
Mitchell, B. G., Brody, E. A., Holm-Hansen, O., McClain, C., and Bishop, J., 1991. Light limitation of phytoplankton biomass and macronutrient utilization. Limnology and Oceanography, 36: 16662-1677.
Musgrave, D. L., Chou, J., and Jenkins, W. J., 1988. Application of a model of upper-ocean physics for studying seasonal cycles of oxygen. Journal of Geophysical Research, 93: 15679-15700.
Oguz, T., Ducklow, H., Malanotte-Rizzoli, P., Tugrul, S., Nezlin, N., and Unluata, U., 1996. Simulation of plankton productivity cycle in the Black Sea by a one-dimensional physical-biological model. Journal of Geophysical Research, 101 (C7): 16585-16599.
Radach, G., and Moll, A., 1993. Estimation of the variability of production by simulating annual cycles of phytoplankton in the central North Sea. Progress in Oceanography, 31: 339-419.
Sharples, J., and Tett, P., 1994. Modeling the effect of physical variability on the midwater chlorophyll maximum. Journal of Marine Research, 52: 219-238.
Valiela, I., 1995. Marine Ecological Process. Springer Verlag ed., 686pp.
Varela, R. A., Cruzado, A., Tintore, J., and Ladona, E. G., 1992. Modeling the deep-chlorophyll maximum: A coupled physical-biological approach. Journal of Marine Research, 50: 441-463.
Warren, S. G., Halm, C. J., London, J., Chervin, R. M., and Jenne, R. L., 1988. Global distribution of total cloud and cloud type over the ocean. NCAR Technical Note, NCAR-TN 317.
WHOI, and BBSR, 1988. Woods Hole Oceanographic Institution and Bermuda Biological Station for Research, Station ‘S’off Bermuda, physical measurements 1954–1984. WHOI and BBSR Data Report, MA, 189pp.
Wroblewski, J. S., Sarmiento, J. L., and Flireal, G. R., 1988. An
ocean basin scale model of plankton dynamics in the North Atlantic 1. Solutions for the climatological oceanographic conditions in May. Global Biogeochemical Cycles, 2: 199-218.
Wroblewski, J., 1977. A model of phytoplankton bloom formation during variable Oregon upwelling, Journal of Marine Research, 35: 357-394.
Zhu, J., Kamachi, M., and Wang, D. X., 2002. Estimation of air-sea heat flux from ocean measurements: An ill-posed problem. Journal of Geophysical Research, 107 (C10), DOI: 10.1029/2001JC000995.
(Edited by Xie Jun)
* Corresponding author. E-mail: cxwang@ouc.edu.cn
(Received March 9, 2012; revised October 7, 2012; accepted August 22, 2013)
© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2014
 Journal of Ocean University of China2014年1期
Journal of Ocean University of China2014年1期
- Journal of Ocean University of China的其它文章
- Surface Heat Budget and Solar Radiation Allocation at a Melt Pond During Summer in the Central Arctic Ocean
- QSAR for Photodegradation Activity of Polycyclic Aromatic Hydrocarbons in Aqueous Systems
- Study on Deformation Law of Circular Foundation Under Combined Loading
- A Model Study on Dynamical Processes of Phytoplankton in Laizhou Bay
- Properties of Klebsiella Phage P13 and Associated Exopolysaccharide Depolymerase
- Seasonal Distribution of Bioaerosols in the Coastal Region of Qingdao
