基于GIS的海水环境监测站位优化*
——以胶州湾为例
尹维翰,崔文林,齐衍萍,鞠 莲,宋文鹏,赵玉慧
(1.国家海洋局北海环境监测中心 青岛 266033;2.国家海洋局海洋溢油鉴别与损害评估技术重点实验室 青岛 266033;3.中国海洋大学海洋地球科学学院 青岛 266100)
基于GIS的海水环境监测站位优化*
——以胶州湾为例
尹维翰1,2,3,崔文林1,2,齐衍萍1,2,鞠 莲1,2,宋文鹏1,2,赵玉慧1,2
(1.国家海洋局北海环境监测中心 青岛 266033;2.国家海洋局海洋溢油鉴别与损害评估技术重点实验室 青岛 266033;3.中国海洋大学海洋地球科学学院 青岛 266100)
文章利用2003—2012年5月、8月和10月胶州湾19项海水监测要素归一化后数据,基于Arc GIS软件地学统计模块,通过Kriging插值模型对归一化数据进行检验分析及站位优化。结果表明,优化后的31个监测站位估计误差标准差梯度较优化前大幅降低,平均估计误差标准差由0.160降低到0.147,降低了8.3%。站位优化后不仅可对胶州湾沿岸重点污染源以及胶州湾海域总体海水质量实施有效监控,并且可以作为今后胶州湾海水监测的常规站位。优化后的监测网在满足监测精度需要的同时,能够较大程度节省监测网的运行费用,可以为其他海域海水监测站位优化及海洋主管部门提供技术支撑,具有重要的应用价值。
站位优化;地统计;估计误差标准差;胶州湾
当前,全国环境监测进入了蓬勃发展的新时期。伴随环保事业的新发展,环境监测理念不断创新、管理不断强化、技术不断进步、投入不断增加、队伍不断壮大,尤其是“十一五”以来,我国环境监测从认识到实践都发生了深刻的变化,已经从传统的技术层面,融合到环境保护工作的整体之中,成为探索中国环保新道路的重要支撑。“十一五”期间,国家环境监测网生产监测数据1亿多个,出具各类环境监测报告8 000余份,为服务宏观决策、支撑环境监管、满足公众需求、支持环境履约发挥了重要作用[1]。
随着党的十八大提出要“提高海洋资源开发能力,保护海洋生态环境,建设海洋强国”,我国的海洋环境监测工作进入了新的里程,对海洋环境监测有了更高的要求。而海洋监测站位布设关系着海洋环境监测工作的成败,优化布点是体现环境监测科学性的重要环节。任何环境要素的监测点常需经历一个由少到多、又由多到少的探索过程。在一定空间范围内布设的测点数量大,虽然能较好地反映环境质量状况,但却需要较高的经济代价[2]。本研究为解决上述问题,立足于海洋环境管理部门掌握的监测数据,以地理信息系统为工具,结合国内外相关研究领域监测网建设的经验[3-4],以胶州湾海域为例建立了海水环境监测站位布设优化新方法。
1 设计原理
在海洋环境系统中,测量是对海洋环境主要素的时、空监测,提供实际海洋环境系统变化的信息;模型是对概化的海洋环境系统进行定量化描述,以提供海洋环境系统状态的估计(用Kalman滤波和Kriging方法)。测量和模型构成对海洋环境系统状态估计时必须的两个重要手段。测量具有测量误差(也称作噪声),模型具有系统误差(也称作系统噪声)。而估计误差的标准差与测量误差的方差、系统误差的方差及选用的算法有关[5]。
海洋环境监测站位最优设计中估计误差标准差愈小,要求估计算法、测量及系统模型愈精确,要使海洋环境监测运行效益高,即海洋环境信息提取的损失量就要小。另外,测量、系统模型和估计算法愈精确,要求海洋环境监测网的费用愈高[4]。最佳海洋环境监测应是损失量最小(图1)。因此,通过一些概化或采用代用目标,可以实现给定条件下的海洋环境监测网优化问题。如,在给定海洋环境监测网设计费用的条件下,优化设计海洋环境监测网使估计误差的标准差最小(图2)。

图1 估计误差标准差与费用和损失关系
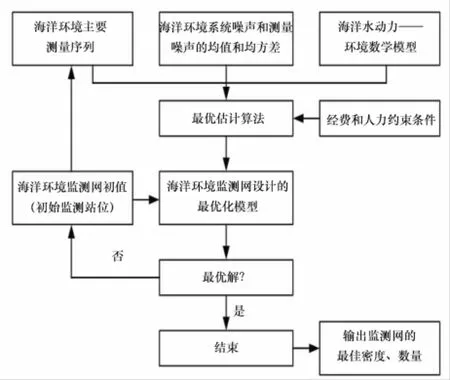
图2 给定经费约束条件下的海洋环境监测网优化设计过程
2 最优估算方法的确定
2.1 地统计插值模型
Kriging法是建立在地质统计学基础上的一种方法,区域化变量和半方差是Kriging插值法的基础,它是一种对时、空分布变量求最优、线性、无偏内插估计的方法[6-7]。根据已知监测站位的数据,对其进行结构性分析后,利用待测点周围监测站位的已知数据和被赋予的权系数,进行加权平均来获得待测点的数值[8]。
Kriging函数模型:
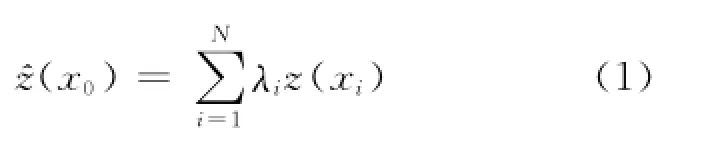
利用式(1),在保证无偏性和最优性的前提下,结合协方差定义,并引入拉格朗日算法,可得:
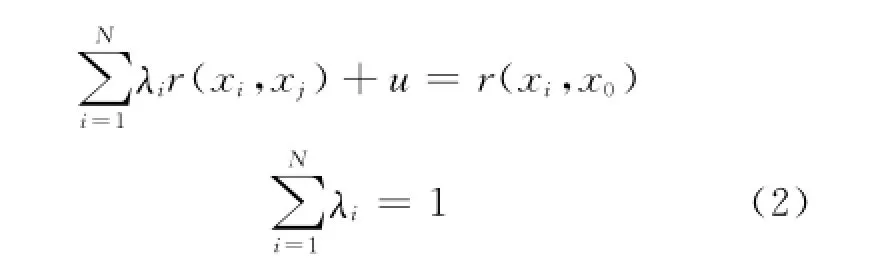
利用式(2)并注意方差函数、协方差函数、变差函数在本征条件下的转换关系,可得计算误差的理论方差为:

根据实际需要,用方差减少法进行,当给定估计误差的标准差(根据研究区环境要素空间分析、监测精度要求及财力要求确定),就可以确定最佳监测站点。
2.2 变差函数
变差函数既能描述区域化变量的空间结构性,又能描述随机性,它是地质统计学计算的基本工具。理论上变差函数的表达式:

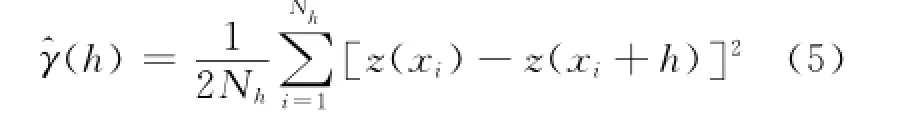
利用式(4)计算不同h对应的^r(h),再根据最佳曲线拟合原理进行曲线拟合得到^r(h)关于h的最佳拟合曲线。常见的变差函数模型有:球状模型、高斯模型、指数模型。在计算变差函数的过程中要与具体的海洋环境条件相结合。
2.3 阶数N的确定
在采用Kriging法对某站位海洋环境标准值估计时,理论上整个研究区内站位均需要参与计算。但实际上,某一站位只与相近区域的站位有关,距离越远相关关系越小,若所有点的均参与计算容易产生病态,为了避免这种现象的发生,本研究中采用“内圈层”的5个监测点进行计算[10]。
3 胶州湾海洋监测站位优化
3.1 研究区概况
胶州湾位于山东半岛南部,胶州湾口窄内宽,东西宽27.78 km,南北长33.3 km(低潮位时),面积446 km2,为伸入内陆的半封闭性海湾。胶州湾沿岸有海泊河、李村河、楼山河、墨水河、大沽河、跃进河和前湾诸河等主要入海污染源;胶州湾口北部为青岛港,是黄海沿岸水运枢纽,山东省及中原部分地区重要的海上通道之一;湾口西南方为黄岛油码头,是中国三大专用原油输出码头之一。因此,胶州湾与周边城镇、河流、港口等已构成了一个多元化复合生态体系[11],是研究海洋监测站位布设理想的示范研究区。
3.2 监测要素值标准化和归一化
胶州湾海水环境监测监测要素包括营养盐、石油类和重金属等19项指标,各指标序列因权重、量级以及单位的不同需进行标准化处理,从而消除不同量纲所产生的影响。还应进一步归一化处理,使不同因子及各站位数据之间具有可比性,而经过这样处理后并不影响各因子子序列与母序列的相关性[12-13]。本研究选取2003—2012年5月、8月和10月胶州湾海水监测结果,对各监测站位监测要素归一化后结果见表1。

表1 胶州湾各监测要素值标准化和归一化结果(2003—2012年)
3.3 站位优化结果与讨论
利用ArcGIS软件地学统计模块,通过Kriging插值模型分别对海水监测归一化后数据进行检验分析评价,估计任一点估计误差的标准差,进而得到估计误差标准差等值线图。估计误差标准差仅与变差函数的类型和监测站位的位置有关,而变差函数反应海水监测体系的结构性特点。在经费一定和周边污染源、水动力环境变化不大的情况下估计误差标准差仅与监测站点的位置和数量有关,并与监测站点分布密度呈反向关系,即在监测站点密度大的地方,其值偏小;反之则偏大。
现有胶州湾海水环境监测站位估计误差标准差见图3,平均标准差为0.160。从整体看,胶州湾中部和南部区域估计误差的标准差较小,而在胶州湾沿岸和北部区域,估计误差的标准差大;在观测站位密的地方估计误差标准差小,反之则误差标准差大。这是由于在胶州湾北部沿岸受墨水河、大沽河、跃进河和红岛养殖区等的影响估计误差标准差较大;东部沿岸受青岛港的影响在青岛港区域估计误差标准差较大;中部沿岸由于对海湾大桥工程实施跟踪及后续监测,监测站位较密,因此估计误差标准差较小;南部海西湾虽然有前湾诸河及黄岛港的影响,但由于对海西湾实施了重点监测,因此估计误差标准差较小。

图3 胶州湾现有海水环境监测站位估计误差标准差
胶州湾海水监测站位优化后删除了3个监测站位,增加了6个监测站点,共设计31个监测站点。新增站位主要位于墨水河口、大沽河口和跃进河口等近岸污染源排放较大的海域;调整站位集中在海湾大桥周边观测较密的站位,剩余89%的站位为了保持历史数据的可比性并未对其调整优化。按照该方案优化后估计误差标准差梯度较优化前大幅降低(图4),平均估计误差标准差为0.147,降低了8.3%(图5)。

图4 胶州湾优化后海水环境监测站位估计误差标准差

图5 胶州湾监测站位估计误差标准差与监测站位数的相互关系
4 结论与建议
利用ArcGIS软件地学统计模块,对胶州湾海水监测站位优化后监测站位基本覆盖了胶州湾,该方案可对胶州湾沿岸重点污染源以及胶州湾海域总体海水质量实施有效监控,并且监测估计误差标准差较优化前大幅降低了8.3%。因此,优化后的31个站位能较好地代表胶州湾海域的海水环境质量,可以作为胶州湾海域今后海水监测的常规业务化监测站位。
由于人们对海洋环境的认识,是通过监测数据的分析识别的。因此监测站位优化是一个过程,不是一次就可以完成的,它是通过不断监测、不断验证和调整,逐渐完善的过程。经过几年的优化站位、验证监测,最终可使得监测站位达到最优化状态。优化后的监测网在满足监测精度需要的同时,能够较大程度地节省监测网的运行费用,可以为其他海域海水监测站位优化及海洋主管部门提供技术支撑,具有重要的应用价值。
[1] 万本太.浅谈国家环境监测网建设[J].中国环境监测,2011,12,27(6):1-4.
[2] 中国环境监测总站.环境水质监测质量保证手册[M].北京:化学工业出版社,1994:10-11.
[3] OZKUL S.Entropy-based assessment of water quality Monitoring networks[J].Journal of Hydrologic Engineering,2000(1):90-100.
[4] 屈泽伟,张翼龙,王贵玲,等.内蒙古呼和浩特市承压地下水水位监测网优化[J].地球学报,2013,34(3)(2):223-228.
[5] HUDAK P F,LOAICIGA H A.A location modeling approach for groundwater monitoring network augmentation[J].Water Resources Research,1992,28(3):643-649.
[6]MATHERON G.The intrinsic random function and their applications[J].Advances in A pplied Probability,1973(5):429-468.
[7] 刘瑞民,王学军.湖泊水质参数空间优化估算的原理与方法[J].中国环境科学,2001,21(2):177-179.
[8] 何雨江,靳孟贵,刘延锋,等.南疆棉田表层土壤盐分的空间变异特征分析与应用[J].地质科技情报,2010.29(6):90-92.
[9] 周在明,张光辉,王金哲,等.环渤海低平原水土盐分与水位埋深的空间变异及协同克立格估值[J].地球学报,2011,32(4):493-499.
[10] 矫希国.变差函数参数的计算[J].地质论评,1997,43(6):659-663.
[11] 郭东辉,殷月芬,陈发荣,等.胶州湾表层沉积物重金属污染分布特征及其生态风险评价[J].环境污染与防治,2012.3,34(3):12-21.
[12] 尹维翰,曹志敏,蓝东兆,等.象山港颗粒有机碳的分布及其影响因子[J].海洋环境科学,2007,26(6):550-567.
[13] 李峋,仵彦卿,范海梅.高维空间插值在海洋环境数据预处理中的应用[J].海洋环境科学,2009,28(6):729-733.
国家海洋局海洋溢油鉴别与损害评估技术重点实验室项目——近海海底持续溢油事故次生海水环境问题研究(201308);北海区海洋环境质量综合评价方法[DOMEP(MEA)-01-01].

