AR 模型在宝珠寺水库实时洪水预报校正中的应用
陈 攀 ,姜志群
(1. 华电四川发电有限公司宝珠寺水力发电厂,四川 广元 628003;2. 南京江山同和水利水电技术有限公司,江苏 南京 210000)
0 引言
水文系统是一个受多种因素影响的复杂系统,这些影响因素大多具有不确定性的时变特征。尤其是人类活动对流域下垫面的影响,包括流域内大量小水电的开发及引调水工程的建设,使得洪水预报精度难以令人满意。
自 20 世纪 70 年代以来,随着计算机的普及应用,水文模型得以广泛应用,实时预报越来越受到关注。但由于人类活动对流域下垫面的影响,实时预报精度很难达到生产要求。故在实际洪水预报作业中,实时校正是一个不可或缺的部分。实时校正从方法论上可分为 3 类:1)滤波方法,包括卡尔曼滤波[1]、自适应滤波等;2)时间序列方法[2];3)人工智能方法[3],包括人工神经网络、进化算法等。3 种方法各有优劣,具体如下:卡尔曼滤波适用于任何线性随机系统,如果预报模型选用合适,预见期和预报精度都不会损失,但该法使用条件多,且有大量的矩阵计算,许多流域难以满足,实际应用时需要灵活处理;时间序列法以误差序列的自相关作为校正方程,方法简单,计算量小,应用较多的是AR 模型;人工智能方法目前实际应用较少,尚处于试验阶段,不能确定校正的实际效果。由于时间序列模型结构简单,要求资料相对较少,在生产上得到广泛的应用[4-5],四川宝珠寺水库就采用时间序列AR 模型进行实时洪水预报校正。
1 实时预报模型
宝珠寺水库以上流域多年平均降水量为 820 mm,多年平均入库径流量为 106 亿 m3,属于半湿润地区,从水文气象特征及入库流量过程性态分析,该地区预报模型可选用新安江模型。
新安江模型为分散参数的概念性模型,结构简单,参数少且具有物理意义,模型的参数必须根据历史资料进行率定。新安江模型根据流域雨量站网的分布,用泰森多边形法将全流域分成为许多单元子流域,对每个单元子流域作产汇流计算,得出单元子流域的出口流量过程,再进行出口以下的河道洪水演算,求得流域出口的流量过程。把每个单元子流域的出口流量过程相加,即为流域出口的总出流过程。分散性主要考虑影响产流诸因素在流域面上分布的不均匀性,诸如降雨分布及下垫面不均匀性的影响,防止均化对预报结果的影响。在每个单元流域上,应用流域蓄水容量曲线考虑土壤含水量面上分布的不均匀性对产流的影响。新安江模型总径流分为地面径流 RS、地下径流 Rg、壤中流 RI等 3 部分。模型的蒸散发部分采用 3 层蒸发模型,即上层蒸发 Eu,下层蒸发 EL和深层蒸发 ED。模型的汇流计算统一采用汇流曲线法。
新安江模型已广泛用于中国许多地区的洪水预报作业中,应用表明,新安江模型适用于中国湿润半湿润流域,具有良好的精度。
2 实时校正模型
宝珠寺水库上游建有碧口水库,几年前在碧口水库下游又建了河床式电厂,对宝珠寺水库入库流量产生了人为的调节作用,干扰了宝珠寺水库正常的预报过程,使宝珠寺的预报与实际过程产生较大的偏差,需要对预报过程进行实时校正。由于宝珠寺水库入库缺乏水文站控制,无法通过入库站采用其它方法进行预报校正,同时受到资料条件的限制,所以本研究采用时间序列方法进行实时校正。
实时校正的变量可以是预报模型的参数,也可以是预报误差或状态变量,但大多数是对预报误差系列进行校正。对预报参数进行校正存在较大的风险,因为预报模型参数是通过长系列历史洪水资料进行率定得到的,基于历史的平均情况,同时水文模型参数在某种意义上具有一定的物理意义,对模型参数进行校正可能会因某一场特殊分布的洪水得出不符合参数物理意义的参数值。同时,由于洪水预报误差序列具有拖尾的特性,且为白噪声,故洪水预报误差序列为平稳时间序列,可采用时间序列AR 模型进行实时校正。
AR 模型为预报误差自相关模型,反映了预报误差的前后相依特性,误差序列的拖尾性反映了这种相依性。作业预报中,根据前几个时段的实测流量和预报流量的误差,由校正模型(AR 模型)计算出预报时刻的误差量,将其加到新安江模型的预报值上,即为该时刻的预报流量。
AR 模型的阶数由 AIC 准则确定,模型的系数由最小二乘法确定。

式中:p 为模型阶数;xt为误差项;{εt}为白噪声序列。
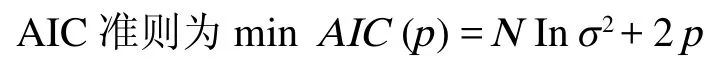
使得 AIC 信息量取值最小的 p 值,即是模型理想的阶。AIC 信息量由 2 部分构成:前一部分体现模型的拟合好坏,后一部分表明模型参数的多少。显然希望模型拟合得越精确越好,但过高的精度要求又会导致参数的增多及模型的复杂,反而会影响模型的拟合效果,因此,实质上,AIC 信息量就是对拟合精度和参数个数两者加以适当权重,AIC 的最小值处对应着最佳模型的阶数。
3 参数校准
3.1 降雨径流模型参数校准
新安江模型参数包括蒸散发折减系数 K;张力水容量 WM,分为上层 WUM、下层 WLM和深层WDM;张力水蓄水容量曲线的指数 B;不透水面积的比例 IMP;深层蒸散发系数 C;表层土自由水容量SM;表层自由水蓄水容量曲线指数 EX;表层自由水蓄水库对地下水和壤中流的出流系数 KI和 Kg;地下水库和深层壤中流的消退系数 Cg和 GI;滞后演算法中的滞后时间与河网蓄水消退系数 L 和 CS。
新安江模型参数的率定是分层次进行的。首先用日降雨、日流量、日蒸发资料对模型水量平衡参数进行校准,日模型校准的准则采用实测年径流与模拟年径流差最小,确定性系数 DC最大。
利用洪水过程资料对模型影响洪水过程的参数进行校准,次洪模型校准的准则采用实测洪峰流量与模拟洪峰流量差最小,且确定性系数最大,并综合考虑洪峰滞时。
最后,综合日模型和次模型率定成果,统筹考虑确定新安江模型使用的参数。
3.2 AR (p) 模型的定阶和参数的确定
用新安江模型计算出模拟流量过程后,与实测(反推)流量过程相减,得到预报误差过程系列。然后对预报误差系列进行白化处理(零均值化),即误差系列减去均值,得到零均值化后的残差系列。计算后的残差系列均值为 0,方差为有限值。取不同的 p 值,计算残差系列的 AIC 值,取 AIC 最小值所对应的 p,即为该模型的阶数 p。根据最小二乘法,计算 AR(p)模型的系数。
4 实例研究
本实例选用宝珠寺水库实时洪水预报模型利用AR 模型进行校正。宝珠寺水电站位于四川省广元市境内白龙江下游宝轮镇附近,以发电为主,兼有灌溉、防洪等综合效益。总装机容量 70 万 kW,设计年发电量 23.5 亿 kW 时,大坝坝顶全长 524.5 m,最大坝高 132.0 m,水库总库容 25.5 亿 m3,调节库容13.4 亿 m3。电站具有不完全年调节能力,承担着四川省电网调峰、调频和事故备用重任。宝珠寺水库坝址以上流域面积 28428 km2,坝址多年来平均流量336 m3/s,多年平均年径流量 106 亿 m3。
由于宝珠寺水库所处海拔高程较大,年蒸发量较大,需对模型结构进行适当的修改,主要对流域3 层蒸发结构进行调整,考虑分汛期和非汛期设置深层蒸发系数 C。经率定,汛期深层蒸发系数为0.2,非汛期为 0.1。
选用宝珠寺水库 2001—2010年10 年资料,包括各雨量站逐日降雨量、逐日入库流量、逐日蒸发量、次洪入库流量过程及其对应的各雨量站降雨过程,对新安江和 AR 模型参数进行率定。根据模拟与实测流量误差系列,确定 AR 模型的阶数为 2。用 AR 模型校正后,校正前后的流量误差系列如图 1所示。实时校正前后实测与模拟年径流误差统计如表1 所示。由表1 可见,经校正后,精度有了较大的提高,平均绝对误差由 1.10 降低为 -0.41,平均相对误差由 -1.33% 降低为 -0.64%,最大相对误差由14.05% 降到 -8.80%,平均确定性系数由校正前的0.84 提高到校正后的 0.94。
用 2011年8月26日和 2012年7月3日次洪对实时预报和校正模型进行检验,结果如图 2 和 3所示。
由图 2 和 3 可见,实时预报模型加了实时校正模型后,对预报洪水过程精度有明显的改进,尤其是洪水过程的拟合更令人满意。2011年8月26日次洪实测洪峰流量为 1331 和 1610 m3/s,预报为 1197和 1579 m3/s,校正后为 1443 和 1760 m3/s;校正前预报相对误差为 -10.07% 和 1.93%,校正后预报相对误差为 8.39% 和 -9.31%;校正前确定性系数为0.86,校正后为 0.97。2012年7月3日次洪实测洪峰流量为 1847 m3/s,预报为 1877 m3/s,校正后为1865 m3/s;校正前预报相对误差为 -1.64%,校正后为 -0.97%;校正前确定性系数为 0.87,校正后为0.99。
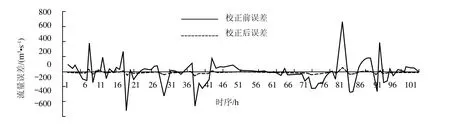
图1 校正前后的误差系列
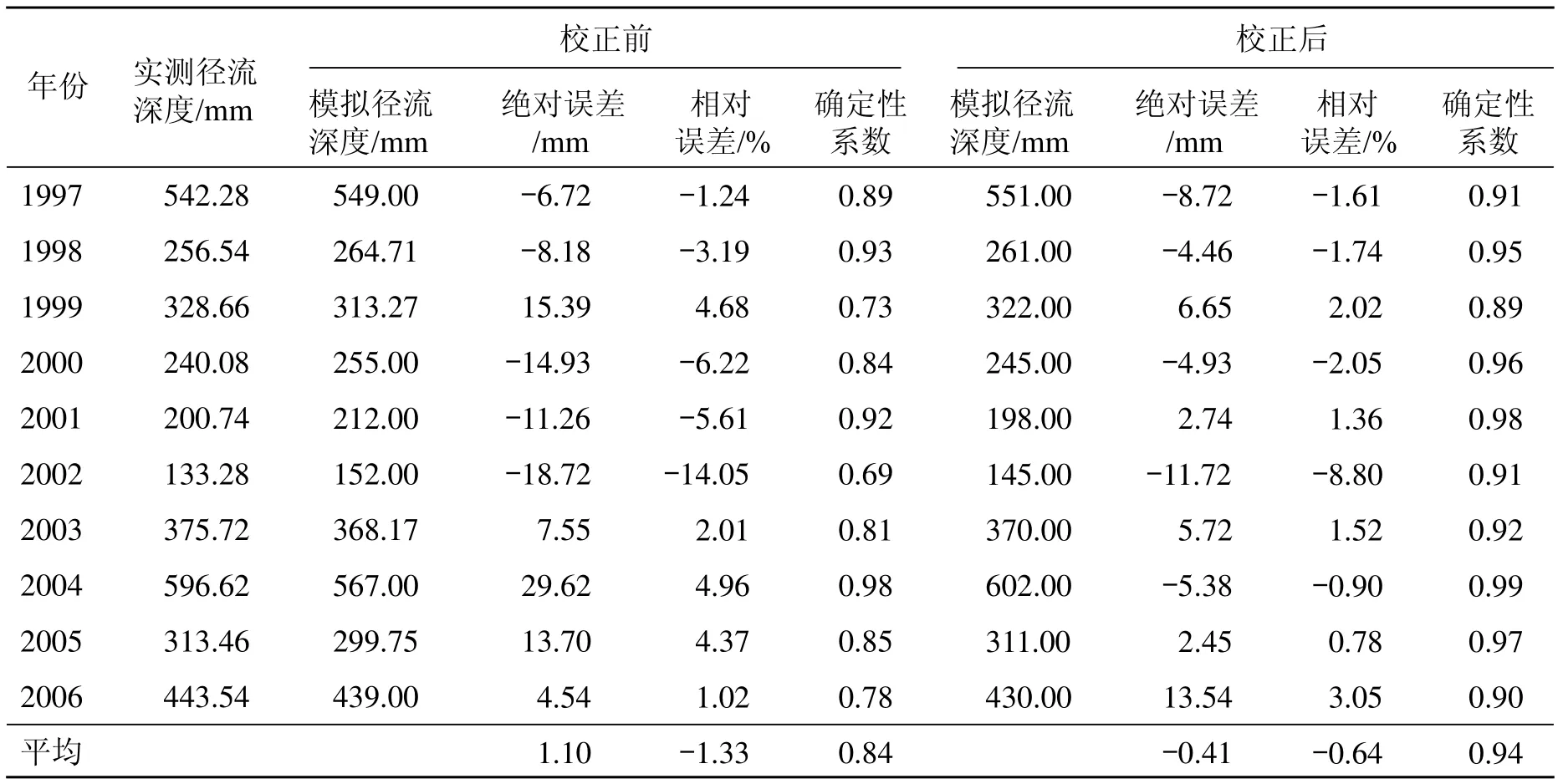
表1 实时校正前后误差统计表
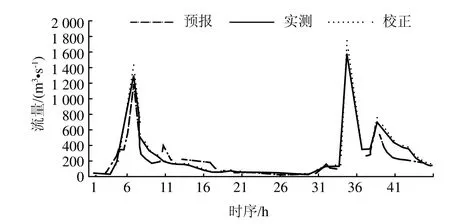
图2 2011年8月26日次洪实测、预报、校正洪水过程
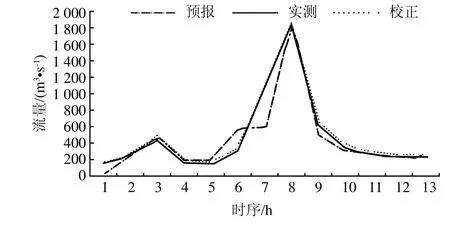
图3 2012年7月3日次洪实测、预报、校正洪水过程
5 结语
人类活动极大地改变了流域下垫面特性,使得单一洪水预报模型预报精度很难达到生产要求,必须对洪水预报进行实时校正。由于洪水预报误差具拖尾特性和接近于白噪声,属于平稳时间序列,可用时间序列模型进行实时校正,时间序列模型作为实时校正模型在实际生产中得到广泛应用。宝珠寺水库受人类活动干扰很大,常规预报模型精度不足,加入 AR 模型进行校正后,精度明显提高,特别是对洪水过程的拟合更为理想。由于 AR 实时校正模型本身是依赖于预报误差相依特性的,其对洪峰附近(曲线拐点处)的流量和滞时可能校正不够,影响预报精度。与人工智能等实时校正模型相比,时间序列实时校正模型概念更加清楚,在资料充分的情况下模型制作更加简单,且使用更加方便。
[1]宋文饶. 卡尔曼滤波[M]. 北京:科学出版社,1991: 123.
[2]王必义. 应用 AR (P) 模型预测水文系列[J]. 河南理工大学学报:自然科学版,1993 (3): 58-66.
[3]丛日凡,姜志群,张淑芬,等. 水库洪水预报实时校正算法[J]. 水土保持应用技术,2010 (4): 31-33.
[4]赵超,洪华生,张格平. 实时校正模型的抗差递推算法[J]. 中国科学院研究生院学报,2008 (5): 666-670.
[5]瞿思敏,包为民,石鹏,等. AR 模式误差修正方程参数抗差估计[J]. 河海大学学报:自然科学版,2003 (4):497-500.

