烯丙基酚氧树脂改性双马来酰亚胺体系的优化
江浩等


摘要:通过环氧树脂与二烯丙基双酚A合成了一种烯丙基酚氧树脂,用以增韧双马来酰亚胺。在单因素试验的基础上,根据Box-Benhnken的中心组合试验设计原理,选取改性树脂体系组分为影响因子,应用响应面法进行3因素3水平的18组的设计试验,改性树脂性能(弯曲强度,冲击强度,热变形温度)为响应值,对改性树脂组分配比进行优化。结果表明,改性树脂组分配比BMI、DDS、APO、DABPA、DAP为2∶1∶0.2∶0.84∶0.1(物质的量比)时,综合性能最好,此时改性双马树脂体系的冲击强度可达到21.4 kJ/m2,弯曲强度为200.5 MPa,热变形温度为195.8 ℃。
关键词:烯丙基酚氧树脂;双马来酰亚胺;响应面法
中图分类号:TQ433.4+37 文献标识码:A 文章编号:1001-5922(2014)11-0000-00
1 前言
双马来酰亚胺(BMI)树脂是由聚酰亚胺树脂体系派生出来的一类树脂体系,是以马来酰亚胺(MI)为活性端基的双官能团化合物,其树脂具有与典型热固性树脂相似的流动性和可塑性,可用与环氧树脂相同的一般方法加工成型。同时它具有聚酰亚胺树脂的耐高温、耐辐射、耐潮湿和耐腐蚀等特点,但其自身熔点高,溶解性差,固化物韧性差,这些缺点都成为限制其发展的障碍。因此,必须对其进行改性。BMI的改性途径多,目前行之有效的是用烯丙基化合物与BMI共聚,因为烯丙基化合物能改进BMI树脂的工艺性和韧性而又不降低BMI树脂的耐热性[1~6]。本文以二烯丙基双酚A和环氧树脂为原料,选用胺类催化剂,合成烯丙基酚氧树脂。利用合成的烯丙基酚氧树脂来改性BMI,以期得到性能优越的改性双马树脂体系。基于大量的前期试验,应用响应面法对改性双马树脂体系配比进行优化,研究了体系组分对改性树脂性能的影响,为树脂体系性能优化提供参考。
2 实验部分
2.1 原材料
4,4'-双马来酰亚胺二苯基甲烷(BMI);4,4'-二氨基二苯砜(DDS);E51型环氧树脂,环氧值0.51;二烯丙基双酚A(DABPA);四甲基溴化铵(TMAB);邻苯二甲酸二烯丙酯(DAP)。
2.2 试样制备
(1)酚氧树脂的制备
将原料DP与EP(物质的量比2∶1)热熔混匀,升温稳定在140 ℃左右后加入0.1% DP质量的催化剂TMAB,反应1 h得到烯丙基酚氧树脂(APO)。
(2)改性双马树脂试样制备
将原料BMI与DDS(物质的量比2∶1)混合均匀,升温至140 ℃预聚,得到扩链双马预聚体(BD),一段时间后降温与DP按配比混合均匀。之后加入改性剂APO反应25 min,降温至120 ℃加入稀释剂DAP,搅拌均匀,倒入已预热并涂有脱模剂的模具中,在真空烘箱中真空脱泡,转移到鼓风干燥箱中固化,自然冷却后经切割、处理得到浇注体试样。
2.3 性能测试
浇注体试样的冲击强度、弯曲强度按GB/T 2567—2008测试,热变形温度按GB/T 1634.2——2004测试。
2.4 实验设计
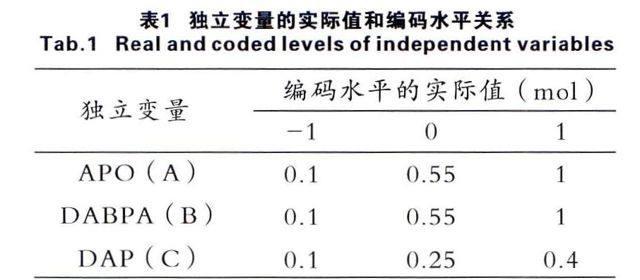
响应面法(RSM)是集数学和统计方法于一身,用来建立和分析几个变量对响应值的影响的一种方法。本文通过Box-Benhnken(BBD)试验设计[7~10],利用Design-Expert软件(8.0.6版本)对改性双马树脂体系进行优化。在本试验中,根据BBD实验设计原理,建立重复六次的中心点,设计了18个配比的试验。保持BMI(2mol)和DDS(1mol)的摩尔常数不变,以改性树脂体系里面其他3组分为3个独立变量因素(分别为系数A是APO,B是DABPA,C是DAP)进行响应面分析,来建立合理的数学模型预测其性能。每个因素3个水平,以(-1,0,1)编码,其响应值y1、y2、y3分别是固化改性树脂弯曲强度,冲击强度和热变形温度。变量因素编码与实际值的对应关系如表1所示。依据前期大量实验,所有因素的取值均在合理的范围之内。
表2给出了全部BBD试验设计安排及其预测值和对应的实验值,所有预测响应值都是根据BBD模型计算而来。一般来说,BBD二阶模型响应值和自变量之间的关系可用公式(1)表示:
式中Y表示与变量xi一致的响应值。b0、bi、bii和bj是由模型估计的回归系数,xi和xj是自变量的水平,e为标准误差。
本实验中,对实验数据进行统计分析,通过多元回归分析建立了相应的二阶多项式方程。通过方差分析(ANOVA)和决定系数分析(R2)评价模型的合理性,最后利用模型得出一系列优化改性树脂配方。
3 结果与讨论
3.1 拟合模型的统计分析
如表2所示,试验设计所得的实验数据用来建立模型关联自变量与响应值。通过方差分析建立足够精确的模型,各响应值对应模型的二阶多项式方程如式2,3,4所示。
P值可以用来检查系数的显著性,同时也表明每个独立变量之间的相互作用程度。P值越小,其相应的系数对响应值的变化贡献越显著。本实验中用F检验和P值检查每个因素对其响应值影响的显著性。表3给出了弯曲强度,冲击强度和热变形温度模型的方差分析结果。基于方差分析表,可以明显地看出F检验值非常低(P<0.0001),这说明3种模型都是高度显著的模型。失拟检测(Lack of fit)用来表示模型单次误差与重复多次误差的显著性,从表3可以看出,Y1,Y2,Y3的失拟检测值都不显著,这说明3种模型准确度较高。
同样的可以在表3中看出,Y1的系数和Y2(B除外)的系数以及Y3的3个系数(A、B、C)都显著。因此,对于Y1和Y3,独立变量A、B、C是显著因素,而对于Y2,独立变量A、C是显著因素。表4列举了变异系数(Y1的C.V.%= 1.5, Y2的C.V.%= 4.3, Y3的C.V.%= 2.7),拟合度(Y1的R2=0.9932, Y2的R2=0.9734, Y3的R2=0.9951)以及校正拟合度(Y1的R2Adj=0.9912, Y2的R2Adj=0.9386, Y3的R2Adj=0.9914)。这些值表示,3个模型的通用性和精度已经足够,并且可以看出3个模型所有的预测拟合度(Y1的R2Pred=0.9583, Y2的R2Pred=0.8862, Y3的R2Pred=0.9698)与其对应的校正拟合度相差不大。另外,精密度(Adeq precision)是有效信号与噪声的比值,大于4视为合理。3个模型的信噪比均远远大于4,这说明3个模型足够应用于响应值的预测。
如果残差落在一条直线上,表明误差是正态分布的。弯曲强度Y1、冲击强Y2和热变形温度Y3的残差正态概率图见图1,3个图上的点几乎都是形成一个是线性趋势,这表明该模型都是标准的良好模型。图2分别显示了Y1 、Y2和Y3 残差与预测值关系。图中表明,所有的实验数据点周围响应变量的均值均匀分布。这意味着,提出的模型是正确的,而且也没有违反独立性或常数方差的假设。
3.2 交互效应
响应面图可以直观地提供实验因素和响应值之间的相互关系,可以方便地对各因素与响应值之间的关系进行研究。3个模型的三维响应面和二维等高线图如图3,4,5所示,它表示了3个独立变量中的任意一个变量维持在零编码水平时,其他2个变量与固化树脂的弯曲强度、冲击强度和热变形温度之间的影响关系。
在图3(a)中,根据图形可以看出,随着APO或DABPA变大,弯曲强度值在增加。此外如果APO在一个固定水平时,随着DABPA的变化,弯曲强度的变化呈抛物线形,反之亦然。在图3(b)中可观察到类似的结果。图3(c)表示,热变形温度值随着APO的变大呈线性增加,而随着DABPA的变大略微的均匀下降。在图4(c)中的APO和DAP以及5(c)中的DAP和DABPA有类似的情况。图4(a)是APO和DAP对弯曲强度的影响图,可以看出随着DAP的增加,弯曲强度略有下降,而随着APO的增加,弯曲强度先增加到最佳值,然后下降。类似的趋势也可以在图5(a)中看到。图4(b)表明,APO的增加使冲击强度先达最佳值,然后下降,而DAP的增加则先降低冲击强度值到一个最低点,然后再逐步增加,同样地,从图5(b)中也能清楚看出DAP和DABPA以相同的方式影响着冲击强度。
3.3 模型的验证
优化的目标是获得能够同时满足所有自变量变化范围内的最大响应,自变量的值可以通过使用Design-Expert软件求解回归方程来获得。经过求解,选取可行性较高的3个配方,分别进行3次独立的重复,以便验证模型的可靠性。表5列出了最佳条件下对于弯曲强度、冲击强度和热变形温度的预测值和实验值。可以看出3个配方的预测值和实验值的误差均小于5%,证明该响应模型能够充分的优化树脂配方。
4 结论
在前期大量试验的基础上,合理选取各改性树脂组分的取值范围,应用多元二次回归法优化了烯丙基酚氧树脂改性双马来酰亚胺配方。结果表明,APO、DABPA、DAP对改性树脂的性能的影响显著。通过回归分析和模型验证,证明了所建模型的合理性。模型的预测值和实验值的误差均小于5%,说明该方法对改性树脂配方的优化有指导性的意义。而且得到改性树脂组分配比BMI、DDS、APO、DABPA、DAP为2∶1∶0.2∶0.84∶0.1(物质的量比)时,综合性能最好,此时改性双马树脂体系的冲击强度可达到21.4 kJ/m2,弯曲强度为200.5 MPa,热变形温度为195.8 ℃。
参考文献
[1]王汝敏,陈立新.烯类化合物共聚改性双马来酰亚胺树脂的研究[J].粘接,2005,26(5):11 -13。
[2]Ambika Devik,Reghunadhan Nair C P,Ninankn.Diallylhisphenol novolae epoxy system coculred with bisphenol-A-bismakimide cure and thermal properties[J].Jounral of Applied Polymer Science,2007,106(2):1192-1200.
[3]李玲,梁国正,兰立文,等.烯丙基酚氧树脂改性BMI的研究[J].高分子材料科学与工程,1999,16(2):116-199.
[4]Gu Ai-Juan. Novel high performance RTM bismaleimide resin with low cure temperature of advanced composites[J].Polymers for Advanced Technologies, 2005, 16(7):563-566.
[5]程雷,王汝敏,王小建,等.烯丙基化合物改性双马来酰亚胺树脂的研究进展[J].中国胶粘剂,2009,18(4):58-62.
[6]王汝敏,郑水蓉.双马来酰亚胺/烯丙基双酚A共聚树脂的改性研究[J].热固性树脂,1997,(1):16-20.
[7]Eriola Betiku, Sheriff Olalekan Ajala. Modeling and optimization of thevetia peruviana (yellow oleander) oil biodiesel synthesis via musa paradisiacal (plantain) peels as heterogeneous base catalyst: A case of artificial neural network vs. response surface methodology[J]. Industrial Crops and Products, 2014, 53:314–322.
[8]Gueguim Kana E B, Oloke J K, Lateef A, et al. Modeling and optimization of biogas production on saw dust and other co-substrates using artificial neural network and genetic algorithm[J]. Renew. Energy,2012,46:276–281.
[9]Tao Zhu, Hyo Jung Heo, Kyung Ho Row. Optimization of crude polysaccharides extraction from Hizikia fusiformis using response surface methodology[J]. Carbohydrate Polymers, 2010,82:106–110.
[10]Ranjana Yadav, Archana Devi, Garima Tripathi, et al. Optimization of the process variables for the synthesis of cardanol-based novolac-type phenolic resin using response surface methodology[J]. European Polymer Journal , 2007,43:3531–3537.

