关于配置季节性商品仓储面积的模型设计

[摘 要]本文从分析季节性商品对存储面积的需求特性入手，阐述了配置合理的自有仓储面积对经营季节性商品企业的重要性，而后根据季节性商品的特点，提出了建立期望成本优化法模型的观点，最后通过实证研究，验证了该模型的良好效果。本文的主要观点是，季节性商品对仓库储存面积的需求量是个随机数，期望成本优化法模型可以为企业配置较合理的自有仓储面积数。

[关键词]季节性商品；仓储面积；需求量

[中图分类号]F253 [文献标识码]A [文章编号]1005-6432（2014）2-0014-02

1 季节性商品对存储面积的需求特性

季节性商品种类繁多，很多商品都具有季节性特点，如食品、水果、饮料、啤酒、白酒、服装、部分家用电器、旅游用品等。季节性商品旺季和淡季的供求关系有着显著差别。通常销售旺季出现的是供不应求现象，而淡季则很少有人问津，可见季节性商品对仓库储存面积的需求量有以下特性：

一是季节性商品对储存面积的需求量是个随机数。

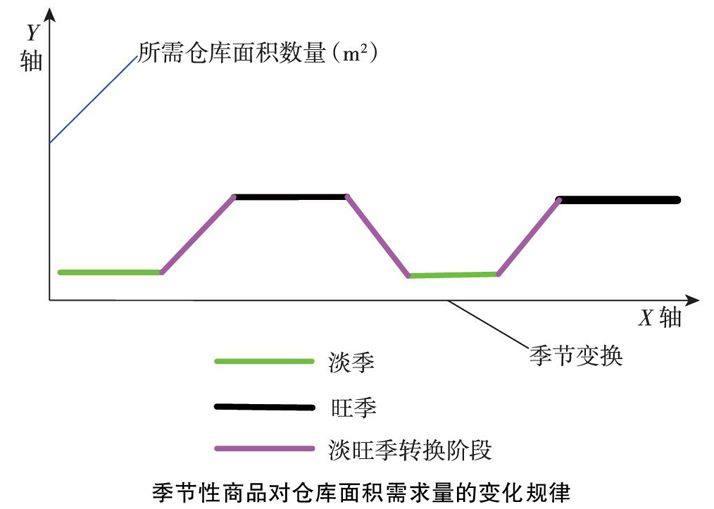
二是季节性商品对储存面积的需求随着季节的变化而不断变化，大部分季节性商品对储存面积的需求量变化情况如下图所示。

三是季节性商品对储存面积的需求量在淡季和旺季时的差别非常大，上下波动很大，如下图所示。

季节性商品对仓库面积需求量的变化规律

很多企业为了应对季节性商品面临的这些特性，常用的做法是，在需求淡季，商品储存量较小时，主要由自有仓库来储存这些商品，到需求旺季，商品储存量大幅增加时，自有仓库面积远远不够，就外租仓库来储存。

但这对企业来说面临的问题就是，应该如何配置合理的自有储存面积，因为如果自有储存面积过大，需求淡季，会出现仓库面积闲置，造成浪费。反之，如果自有仓库面积过少，需求旺季，就要到别处租赁大量仓库，由于租赁仓库成本一般要比自有仓库的成本高很多，因此租赁仓库将增加很多额外的仓库费用，而且租赁仓库有可能增加库存管理的难度，无法达到客户满意的服务水平。

所以，配置合理的仓库面积对经营季节性商品的企业来说非常重要。本文希望通过建立期望成本优化法模型，来帮助企业确定季节性商品合理的储存面积数量。

2 期望成本优化法模型的建立

2.1 问题的提出

季节性商品储存量受到季节性的影响非常大。因此在确定所需仓库面积之前，我们首先要分析该商品过去几年不同季节的需求变化情况。

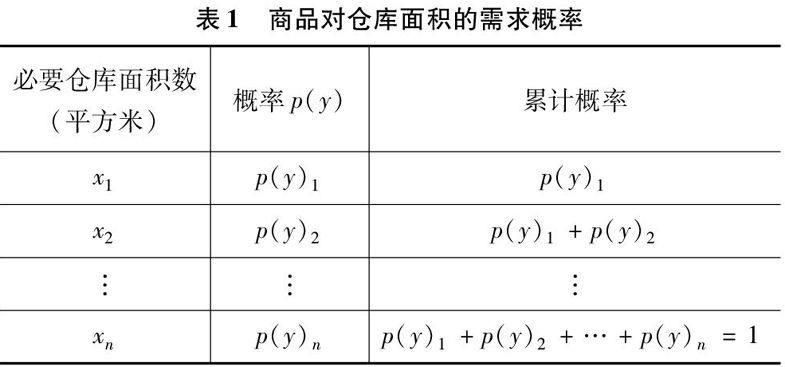
可以通过统计法，找出过去几年季节性商品对储存面积需求数量的分布概率，如表1所示。

表1 商品对仓库面积的需求概率

企业在确定合理的自有仓储面积时，应考虑到业务的发展趋势，对表1中的需求数据进行修正。根据修正后的统计数据得出不同仓储面积的需求概率数及累计频率数，结合以下数学模型，就可算出季节性商品应配置的自有仓库面积数。

2.2 模型假设

（1）自有仓库的服务质量和外租仓库的服务质量没有差异。

（2）季节性商品所使用自有仓库在淡季闲置时无法做其他用途，因此产生闲置费用。

（3）在需求旺季，假设外租仓库随时可以租赁到。

（4）从长期经营看，自有仓库的使用费总是比租赁仓库要低。

2.3 模型构建

以实现仓库运营费用最小为目标构建模型，通过期望成本优化法求解季节性商品合理的自有仓库面积数。

设在每个周期中自有仓库的使用成本为C1，自有仓库的闲置费用为C2，租赁仓库的运行成本为C3。设x为企业自有的合理仓库面积数；y为每个周期实际需要的仓库面积数，y是随机变量，其分布概率为p（y）。

（1）当y≤x时，即实际需要的仓库面积数比企业自有的仓库面积数少，设T为总成本，则企业该周期的总成本为：

T1=yC1+（x-y）C2（使用成本+闲置成本）

（2）当y≥x时，即实际需要的仓储面积数比企业自有的仓储面积数大，自有仓储储存不下的商品全部租赁仓储存放，则企业该周期的总成本为：

T2=xC1+（y-x）C3（使用成本+租赁成本）

（3）设p（y）为对应的概率，则得出企业期望总成本为：

根据概率累计数，可以选取适当的x值，使得上式成立，从而使得仓库运营总成本最小。

因此累计概率所对应的仓储面积数，就是季节性商品应该配置的最佳自有仓储面积数。

3 模型的实际应用

3.1 企业概况

某物流中心主要经营农副产品的库存管理和配送服务，以前对季节性商品所需仓库面积数量的控制比较粗放，淡季时，仓库面积大量闲置，旺季时仓库面积严重不足，到处租借仓库，致使每年仓库管理成本居高不下。

最近公司决定在市郊建立一个大型配送中心，在进行配送中心规模的确定时，公司决定准备重新对市场需求规律进行调查分析，力争为所有季节性商品配置合理的自有储存面积。

公司首先决定对经营量比较大的糖果产品仓库储存面积需求量进行分析，以此作为突破口来找出所有季节性产品的管理策略。

糖果产品具有很强的季节性特点，公司对最近几年的销售数据进行分析后发现，每年的销售旺季在12月到第二年的3月，销售淡季是7月、8月、9月三个月份，其他月份的销售处于相对平稳的变化状况，而对应的所需仓库面积也有类似特征，过去3年里，糖果产品在销售淡季一般安排500～900平方米的仓库面积就可以了，但到了销售旺季，储存量大量增加，对仓库面积的需求有时高达2500平方米以上，这对公司安排仓库面积时带来一定困难，以往公司按照旧的做法，一般为糖果产品配置1800平方米的自有仓库面积，这样做是为了减少在需求旺季去外租仓库的数量，但是经过几年的运作，发现运营成本仍然居高不下，因为在销售淡季，这些自有仓库有一半的空间是闲置的，现在准备重新审视一下以前的仓库管理策略是否合理。

经过统计分析，过去3年糖果商品对仓库面积需求数量的概率如表2所示。

表2 季节性商品对不同仓库面积的需求概率

公司通过市场调查和分析，了解到以下经营成本状况：公司自有仓库使用成本平均为0.5元/平方米·天，自有仓库闲置成本平均为0.2元/平方米·天，公司外租仓库成本平均为0.75元/平方米·天。

那么，公司应该为该糖果产品配置多大面积的自有仓库呢？

3.2 利用期望成本优化模型核算该季节性商品所需自有仓储面积 设自有仓储面积为x，外租仓储面积为y，

这里C1=0.5， C2=0.2， C3=0.75，

引入期望成本优化模型公式，计算累计概率数：

则累计概率数为：

对应表1的累计概率数，累计概率0.56对应的自营必要仓库面积数为1200平方米。即企业应为糖果商品配备1200平方米的自有仓储面积。

通过新模型的计算可以看出，前几年我们为糖果商品配置1800平方米的自有仓储面积，远远超出了1200平方米的合理控制范围。

通过糖果商品这种模型的计算，我们可以进一步核算其他季节性商品的合理仓储配置面积。这为我们规划整体配送中心的面积提供了决策的参考。

4 结 论

期望成本优化法模型可以作为企业在配置季节性商品储存面积时的决策参考工具，如是选择自有仓库还是租赁仓库，以及自有仓库配置面积应该多少才是最合理的。当然企业在确定合理的自有仓储面积时，还应考虑到业务的发展趋势，对历史统计中的需求数据进行修正，根据修正后的统计数据得出不同仓储面积的需求概率数及累计频率数，结合期望成本优化法模型，再算出季节性商品应配置的自有仓库面积数，当然企业应用该模型，还要考虑到自有仓库的其他管理成本、闲置仓库在淡季的再利用、租赁仓库的难易程度、租赁仓库租金的变化、租赁仓库的管理能力和服务水平等因素。

参考文献：

[1]王焰.配送中心规划与管理[M].长沙：湖南人民出版社，2006.

[2]李安华.物流系统规划与设计[M].成都：四川大学出版社，2006.

[3]周永务，王圣东.库存控制理论与方法[M].北京：科学出版社，2009.

[4]邓爱民，张国方.物流工程[M].北京：机械工业出版社，2002.

[5][加]米歇尔·R.利恩德斯，[美]哈罗德·E.费伦.采购与供应链管理[M].北京：机械工业出版社，2001.

[6]陈廷斌，吴赜书.供应链与物流管理[M].北京：清华大学出版社，2008.

[7]李守林.配送中心的功能及其规划设计要点[D].阜新：辽宁工程技术大学，2008.

[8]邢占文，张毅，李金辉.连锁商业配送中心规划决策分析[J].江苏商论，2007（4）：16-17.

[9]方仲民.物流系统规划与设计[M].北京：机械工业出版社，2003.

[10]徐胜余.物流配送中心管理[M].成都：四川人民出版社，2002.

[作者简介]殷延海（1967—），男，上海商学院管理学院副教授。研究方向：物流管理，配送管理。