基于源函数造波法三维数值水槽波浪模拟研究

陆萍

摘 要：波浪是船舶与海洋工程中常见的一种动力因素，对于船舶与海洋结构物，研究波浪的冲击作用对其设计、强度分析等有着重要的意义。随着计算流体力学的快速发展与计算机运算速度的提升，数值造波水池逐渐成为热点且技术日臻成熟，为海洋工程的数值模拟计算提供了良好的基础。本文基于计算流体动力学软件FLUENT，建立了三维数值波浪水槽，以源函数造波法对三维stokes波进行了简单模拟。本计算模型中采用N-S方程与湍流模型，用VOF法进行自由表面追踪，对3种不同工况波浪进行数值模拟，通过数值模拟实验，证明了FLUENT对波浪有良好的模拟效果。

关键词：FLUENT；波浪模拟；VOF

中图分类号：O353.2 文献标识码：A

1 引言

二十一世纪人类全面步入海洋经济时代，如何对海洋资源进行安全有效的开发成为海洋工程界热点问题。海洋结构物在深海中可能会受到波浪、海流、地震等联合作用，而波浪对海洋结构物的冲击作用是最为常见的且为主要荷载之一，因此，研究波浪的冲击作用对船舶与海洋结构物的设计、强度分析等有着重要的意义。随着计算流体力学的快速发展与计算机运算速度的提升，数值造波水池逐渐成为关注的焦点，数值造波技术的日臻成熟为船舶与海洋工程的数值模拟计算提供了良好的基础。

波浪的数值模拟是基于流体运动的基本规律[1]：质量守恒定律、动量守恒定律和能量守恒定律。另外加上波浪理论如微幅波理论来进行程序的编写，最后建立数值波浪水槽或水池来进行模拟研究。其实质是一种数值仿真程序，通过计算机的建模、求解、图形显示，使波浪水槽有了实际水槽的功能，从而进行相关的研究。

建立波浪数值水槽主要的重点有以下四个方面：（1）选择合适的波浪数值模型；（2）数值造波的方法；（3）数值消波的方法；（4）自由表面的处理方法。

20世纪90年代之前，数值模拟的研究范围主要还是以二维为主，二维模拟并不能很好地展示波浪与海洋结构物相互作用中产生的漩涡、波浪绕射等现象，因此三维数值模拟是今后波浪与海洋结构物模拟发展的重要方向之一。

关于波浪的数值模拟，国内外已经有不少的成果：王永学[2]在1993年通过直接差分求解N-S方程，建立了二维数值波浪水槽，很好地模拟出孤立波在直墙式建筑物前推进时的变形、倾覆和破碎过程；封星等人[3]对二维数值波浪水槽在FLUENT中的实现进行了验证，证明FLUENT有很好的波浪模拟能力；齐鹏峭等人[4]在2003年建立的三维数值波浪水池中，对作用在水池中固定长方体浮体结构物上三维水动力荷载进行计算，获得了较好的结果；Li &Lint[5]利用三维数值波浪水槽研究了方柱的绕射。随着计算机技术的不断发展和相关理论的进一步成熟，基于N-S方程建立的描述波浪运动的模型被用在越来越广泛的领域。

2 数值波浪水槽模型

在本文数值水槽中所采用的粘性模型为标准K-ε模型。标准K-ε模型有较高的稳定性、经济性和计算精度，适用于高雷诺数湍流。双方程模型把紊流粘性与紊动能和耗散率k 、ε相联系，建立起它们与涡粘性的关系。K-ε模型是两方程湍流模型中最具代表性的，同时也是工程中应用最为普遍的模型。

在实际的实验水槽中，水槽的底部通常是防锈钢板或防渗水泥抹面，故波浪水槽底部的边界条件为法向速度为零，即为不可穿透条件，FLUENT中将其定义为壁面边界。波浪水槽边壁定义为对称边界，即认为边界两侧都存在流体，水槽最左端静水面以下边界设置为速度入口边界。

在本文中采用体积函数法来计算流场，用流体体积函数法（VOF）求解水气界面。水槽的静水面为水气两相分界面，波浪流动属于水、气分层两相流，适合采用VOF法。同时本文计算采用PISO即压力的隐式算子分割算法。

在本文中采用FLUENT中的自编UDF来对波浪数值水槽进行造波和消波。

3 模型建立与造波

3.1 模型的建立与网格划分

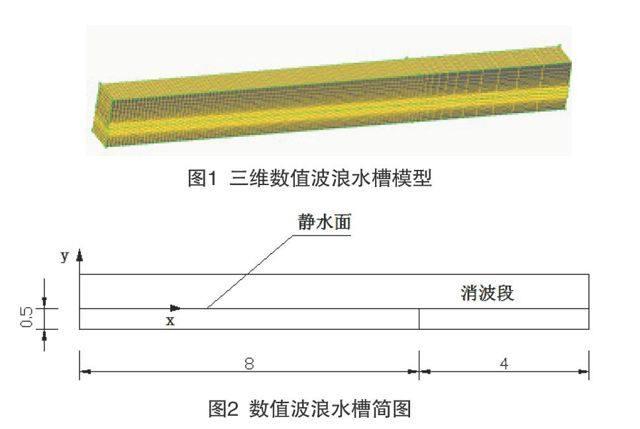
本试验中三维数值水槽模型尺寸为：长12 m、宽0.8 m、高1.3 m，其中水深0.5 m。水槽的左侧静水面以下为速度入口，通过用户自定义函数的加载进行造波。水槽底部为壁面边界，水槽两侧及右端为对称边界，贴近实际情况，并且可以避免两侧波浪的反射。在水槽8 m～12 m范围内进行消波，减少波浪反射对造波的影响。波浪水槽三维简图见图1，平面简图见图2。

图1 三维数值波浪水槽模型

图2 数值波浪水槽简图

由于本试验三种工况的水深都相同，为了简化计算，本文对不同工况下数值模拟波浪都采用同一数值水槽模型。由于不同工况下波高与周期是不同的，每种工况下的用户自定义函数是不同的，以造出符合条件的波浪。

3.2 模型的建立与网格划分

计算网格的合理设计与高质量生成是计算流体力学计算的前提条件。在网格划分之前，先从数值仿真的全局出发，比如精度要求、计算时间要求、计算机配置等，考虑使用结构网格还是非结构网格。在模型比较规则的时候，推荐使用结构网格，结构网格易于划分，计算结果较好，计算时间也相对较短。

在FLUENT中，由于网格的密度对数值模拟的精度与收敛性有很大影响，故在波浪产生的区域内应该用相对密集的网格。本文试验数值模型全部采用结构网格。

3.3 波浪数值模拟验证

波浪数值水槽建好后，下一步就是通过波浪数值模拟试验来确定模型数值造波的可行性。本文设置不同周期的波浪进行对比试验，初步考虑分为三种试验工况，预模拟的波浪周期分别为1 s、1.5 s、2 s，工况具体参数如表1所示。

表1 试验工况

本文中用于造波的UDF的编写依据为微幅波理论，微幅波任意一点处水质点运动的水平分速度u和垂直分速度w分别为：

u= = cos（kχ-ωt） （1）

w= = sin（kχ-ωt） （2）

其中：H为波高；T为波浪周期；d为水深；k为波数；ω为波动角频率；z为波面至静水面的距离。

（1）工况1

在试验水深0.5m、波浪周期1s、波长1.513 m的情况下，距离速度入口边界1m处波高历时曲线如图3所示。

图3 工况1下1 m处波浪历时曲线图

从图3中取出比较稳定的五个波浪，计算得出平均波高为0.112 m。工况1所要求的波高为0.12 m，故1 m位置处波高0.112 m基本符合要求。从波浪历时曲线图中可以看出波浪的形状与波高都无较大变化，证明在此FLUENT数值模型下，对波浪的模拟是成功的。

（2）工况2

在试验水深0.5 m、波浪周期1.5 s、波长2.825 m的情况下，距离速度入口边界3 m处波高历时曲线如图4所示。

图4 工况2下3 m处波浪历时曲线图

从图4中取出比较稳定的五个波浪，计算得出平均波高为0.159 m。工况2所要求的波高为0.15 m，故3 m处的波高0.159 m基本符合要求。由于在水槽尾端并不能完全消去所有入射波，所以还是存在一定的波浪的反射现象，在波浪历时曲线图中可以看出反射波与入射波的叠加导致波浪逐渐爬高，但是此现象并不严重，对数值模拟实验影响不大。

（3）工况3

在试验水深0.5 m、波浪周期2 s、波长4.054 m的情况下，距离速度入口边界2 m处波高历时曲线如图5所示。

图5 工况3下2 m处波浪历时曲线图

从图5中取出比较稳定的五个波浪，计算得出平均波高为0.154 m。工况3所要求的波高为0.15 m，故2 m处波高0.154 m基本符合要求。从波浪历时曲线图中可以看出波浪的形状与波高都无较大变化，证明在此FLUENT数值模型下，对工况3的波浪数值模拟是可行的。

4 结果分析

（1）本次模拟中，数值模型与实际结构物按照1：40的比例建立。Fluent网格的划分对数值模拟实验有着很大的影响，网格的形式与质量直接决定了数值模拟实验结果的收敛性与准确性。按一般情况而言，网格的划分越细，计算的结果准确性越高。但由于计算机硬件条件限制，只能在计算所需时间与结果精度中折中取值，保证实验结果的准确性在可接受范围内。

（2）本文在FLUENT中采用两相流的方法对水气进行分离，并使用VOF法对自由表面进行追踪，以分离式解法中的PISO算法求解流场，使用自己改写的UFD中的宏实现源造波法造波和水槽后端的阻尼消波。通过模拟实验证明了FLUENT有良好的波浪模拟功能，能够很好的模拟不同工况下所需要的波浪条件，且形式简单、计算稳定，有较高的实用价值。但是由于粘性效应，波浪存在衰减现象。

（3）由于在水槽尾端并不能完全消去所有入射波，所以还存在一定的波浪的反射现象，在波浪历时曲线图中可以看出反射波与入射波的叠加导致波浪逐渐爬高的现象。

参考文献

[1] 韩占忠.FLUENT：流体工程仿真计算实例与分析[M]. 北京：北京理工大

学出版社. 2009：2-4.

[2] 王永学. VOF方法数模直墙式建筑物前的波浪破碎过程[J]. 自然科学进

展-国家重点实验通讯，1993，3（6）：553-559.

[3] 封星，吴宛青，吴文锋等.二维数值波浪水槽在FLUENT中的实现[J]. 大连

海事大学学报， 2010，36（3）：94-97.

[4] 齐鹏峭，王永学. 三维数值波浪水池技术与应用[J]. 大连理工大学学报，

2003，43（6）：825-830.

[5] Li CW， Lin PZ. A numerical study of three-dimensional wave interaction with

a square cylinder [J]. Ocean Engineering，2001， （28）：1545-1555.