基于随机模拟的债券免疫决策分析

●蔡达菲

基于随机模拟的债券免疫决策分析

●蔡达菲

对于债券免疫策略决策，传统的分析方法利用债券久期进行套期保值存在很多的局限，未来的债券风险有可能存在不确定性，无法用静态假设反映。文章运用水晶球软件来进行随机模拟仿真运算，并结合案例进行分析，从而帮助投资者做出更加符合现实情景的债券免疫决策。

债券免疫 久期 随机模拟

一、债券免疫的概念

债券久期由Frederick.Macaulay提出，又称“麦考利久期”（简记为D），代表了固定收益债券现金流支付时间的加权平均值。1952年，英国精算师Redington首先提出基于久期的债券免疫理论，并由Bierwag、Kaufman等人发展，直到今天仍被实务界和学术界普遍使用。在不考虑债券的凸性时，其构建的基本要求包括：（1）构造的资产组合的现值之和等于已有负债的现值之和，也就是要求资产足够可以抵消负债；（2）构造的资产久期应等于负债的久期，即构造的资产组合相对于市场收益率的敏感性与已有负债是一样的。久期的计算公式如下：

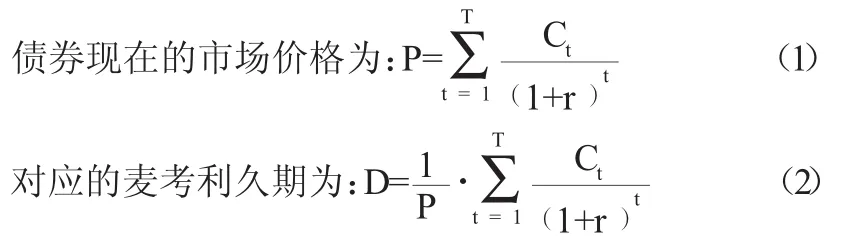
久期实际上就是债券相对于利贴现率的弹性，因此利用久期就可以度量债券的价格相对于利率的波动幅度，从而测量债券的风险。所以债券久期的计算公式又可以表示为（1）式对到期利率求一阶导：

显然，传统的债券免疫策略是基于马克维茨的投资组合理论，并且是建立在对利率敏感度测量的基础之上的。但是，到期利率始终保持不变这一假设使得资产免疫的效果在面对不确定性的市场变动时，显得极为脆弱。债券价格理论对于到期利率的研究表明其主要受到以下几个因素影响：（1）市场利率的变化；（2）期限长度；（3）收不到本金或利息的风险；（4）对现金收入流各种不同税收对待的影响；（5）赎回、回售条款的影响。由此带来的或然性风险有6种：市场利率风险、违约风险、提前偿还风险、通货膨胀风险、汇率风险和流动性风险。其中市场利率风险是主要风险。那么，不变的到期利率是不确定的，传统的资产免疫策略就不能完全表示出这种不确定性，但这种不确定性也不能够用概率的正态分布度量出来的，即其均值并不在一个平均值水平上下波动。作者介绍在债券组合免疫模型中采用随机模拟方法对那些存在不确定性因素的债券进行决策的方法，客观地反映了市场的变化，而大量的数据模拟解释了一种概率的结果，这是人们对传统方法中采用固定利率产生怀疑的一个很好解释。

二、随机模拟方法简介

随机模拟法（Stochastic Simulation）是计算机模拟的基础。该方法来源于普丰的随机投针实验。随机模拟建立在中心极限定理论的基础上，假设先生成大量的随机值，每一次生成随机值就完成一次模拟。如果运行了n次模拟，就会生成n个随机值，其均值就是所需要的估计值。

三、债券免疫策略的随机模拟法

在一个高度市场导向的金融中介体系中，到期利率的不确定性是那些能够使公司的偿债能力处于险境中的最重要的一个因素，也是银行和保险公司管理方面的一个至关重要的问题。到期利率的预测一般而言可以采用均值决策法，但是其忽视了预计因素变动的不确定性。还有一种方法是德尔菲决策，但是将会耗用大量的人力、物力。基于Excel的水晶球软件，可以较为方便地实现债券免疫决策的仿真模拟。

1.水晶球软件概述。水晶球软件是由美国决策工程公司开发的随机模拟技术，在Excel电子表格的基础之上，提供了功能丰富的随机模拟方法。该软件较好地利用了Windows的可视化环境，将很多可见即可得的图片、表格、数据集合到了一起，形成了较为专业的技术组合。水晶球软件包的主要模拟技术含有个人电脑的随机模拟程序、时间数据模拟，以及最优化选择技术，可以在处理结果中自动生成随机模拟的最优解。

2.水晶球软件操作方法。

第一步：在Excel单元格中将债券久期的相关决策模型输入；

第二步：利用水晶球软件的“假设定义”功能为变量方格设定既定概率，利用“决策定义”功能定义决策变量；

第三步：在Excel单元格中，将“预测定义”功能的输出变量进行界定；

第四步：在水晶球软件的“运行参数”中设定好需要模拟的次数等具体参数；

第五步：开始进行随机模拟。

笔者举出一个简化的例子说明预测因素不同水平的变化能够影响债券免疫决策的结果。

四、债券免疫案例分析

假设投资人甲在10年后有一笔债务需要偿还，该笔债务的现值为10000元，当前市场的到期收益率r为6%，假设市场上现在有如下两种债券：

债券A：离到期日还有10年，票面利率为5.8%，面值10000元；

债券B：离到期日还有20年，票面利率为9.5%，面值10000元；

投资人甲通过对以前年度债券市场的分析得出到期收益率的一个概率分布，如表1所示：

首先构造出非随机的债券免疫模型，在Excel电子表格中设置相应的表格内容，如图1所示。其中，C11表示债券A的现值计算公式为：=PV（$C$6，C10，$C$4*C9，$C$4），C12表示用10000元现值应购买的债券A的债券面值：=$C$4/C11*$C$4，C15表示债券A的久期值：=DURATION（DATE（2008，1，1），DATE（C10+2008，1，1），C9，$C$6，1），以此类推债券B的设置。为了构造一个在债券A与债券B之间的资产组合作为免疫策略，再定义C16为固定值10表示债务的久期，C14表示应该购买的债券A的比例：=（C16-D15）/（C15-D15），D14则表示债券B的比例：=1-C14。然后，选择到期收益率作为随机变量，按照预计的概率分布，在Excel中利用水晶球软件设置随机单元格，选定运行参数为10万次、置信区间为95%和定义敏感度分析工具，然后进行仿真运算，可以得到债券A购买比例的统计数据（图2）和概率分布情况（图3）的仿真运算结果。

表1 到期收益率可能取值的概率分布

图1 模型的Excel电子表格

分析图2的随机模拟结果可知，经过10万次模拟运算后，该债券免疫方案的决策结果为：以33%的比例购买A债券，再以67%的比例购买B债券。A债券购买比例的平均期望值为0.33，并且我们还可以得到关于数据模拟的中位数、众数、方差和峰度等参数值。利用图3还可以进行风险分析，这是水晶球软件提供的随机模拟运行结果的其他有用信息。决策者可以在图3中移动图形中的一个三角图标到不同坐标，就可以较快地计算相应区间A债券购买比例的确定性概率（Certainty），图3中使得免疫策略有效，投资人甲购买A债券比例在0.13到0.41之间的概率为59.773%。对于仿真结果的精确度分析，则可以利用图2中统计表底部的均值标准差（mean standard error）提供的数据，真实值一般在样本值的附近变动。本案例中是在95%的置信区间内波动，所以置信区间就是0.33+1.965×0.00=0.33到0.33-1.965×0.00=0.33。随机模拟的值在置信度为95%时就是0.33，这主要是由于购买比例在小数点后两位，因此计算结果认为在该精度下没有误差。根据模拟运算的结果就可以计算出需要花费10000×0.33=3300元购买相应的A债券，花费10000-3300=6700元购买相应的B债券。

图2 统计数据图

图3 概率分布图

五、结论

债券投资管理本身可以说是既是一门艺术也是一门技术，需要一定的方法支持，才能最大限度地发挥债券免疫的作用。笔者在债券久期免疫理论的基础之上，进行随机模拟仿真运算对到期收益率的不变假设进行了放松，并且采用了一个简单易行的模拟软件进行计算，同时实现了免疫策略的可操作性。

[1] 江向东，张列平.债券的定价理论评述，预测，1999（6）

[2] 刘善存.Excel在金融模型分析中的应用.北京：人民邮电出版社，2004

[3] 弗雷德里克.希利尔，马克.希利尔.数据、模型与决策，北京：中国财政经济出版社，2004

（作者单位：中国建设银行常州培训中心 江苏常州 213016）

（责编：吕尚）

F230

A

1004-4914（2014）01-153-02