湿法冶金浸出过程机理模型

周天驰

（江西瑞林电气自动化有限公司，江西南昌 330031）

湿法冶金浸出过程机理模型

周天驰

（江西瑞林电气自动化有限公司，江西南昌 330031）

针对山东某黄金精炼厂的实际工艺，以氰化钠为浸出剂的金浸出过程为背景，基于物料及能量平衡关系,建立了金的氰化浸出机理模型,并通过实际数据对模型进行了仿真,验证了模型的有效性及泛化性。

湿法冶金；金；浸出过程；机理模型；浸出率

湿法冶金相对于火法冶金的显著优点在于原料中有价金属综合回收程度高、有利于环境保护、生产过程较易实现连续化和自动化[1]。而浸出过程作为湿法冶金的一道重要工序,直接决定金属提取的纯度。本文拟针对山东某黄金精炼厂的实际工艺,以氰化钠为浸出剂的金浸出过程为背景,基于物料及能量平衡关系,建立浸出过程的机理模型，并采用实际数据对模型进行仿真,以验证模型的有效性及泛化性。

1 浸出过程

湿法冶金全过程的一般工艺流程为：1)矿石预处理(磨矿);2)矿石原料浸出;3)固液分离;4)溶液净化富集及分离;5)从溶液制取金属或化合物[2-3]。其中浸出过程就是用化学试剂将矿石或精矿中的有用组分转化为可溶性化合物,得到含金属的溶液,实现有用组分与杂质组分的分离过程。本文所研究的是黄金的湿法冶炼工艺，采用的浸出设备为气力浸出槽，利用充入空气在矿浆中的搅拌、溶解作用,使矿浆在槽内运动、循环，让精矿颗粒、浸出剂、空气在矿浆中充分接触,以利于金的溶解。此浸出过程是以氰化钠为浸出剂,同时通入空气增加浸出槽中的氧浓度。氰化浸出过程如图1所示。

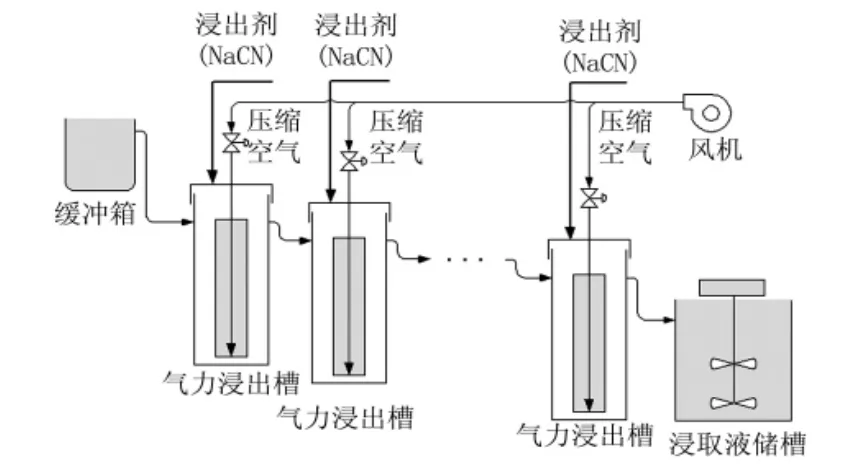
图1 氰化浸出过程示意

浸出过程作为湿法冶金的第一个工序，浸出液的品质好坏直接决定了后面工序提取金属的纯度,因此对浸出过程的研究就显得尤为重要。从浸出过程看,影响氰化浸出的因素主要有浸出剂流量、压缩空气流量、进料流量、溶解氧浓度、矿石粒径、初始金品位等[2]。由于该工艺为连续浸出,因此有多路浸出剂流量和压缩空气流量需要考虑。浸出过程主要的生产指标是浸出率,浸出率直接反应浸出过程的产品质量,目前浸出率的检测方法大多是离线化验检测,检测时间长、成本高，故通常只化验最终的浸出率。因此,建立浸出过程准确的模型来预测浸出率就成为进一步提高湿法冶金自动化生产效率的首要任务。

2 浸出过程机理模型

对浸出过程模型做如下设定：1)模型输入。模型输入包括矿石流量、矿浆浓度、溶解氧浓度、粒子粒径、氰化钠添加量、初始金品位、流入矿浆中氰根离子浓度等内容。2)模型输出。模型输出包括浸出率、浸出后的矿石中金的品位、浸出后氰化钠浓度等。3)反应条件。(1)搅拌槽内矿浆搅拌均匀；(2)搅拌槽内温度分布均匀；(3)忽略反应器中的物料隔离；(4)泥浆的容量阻力恒定[4]。

一般认为在氧存在的条件下，氰化浸金属于电化学腐蚀过程，化学方程可表示为[5]：

综合化学反应方程式为：

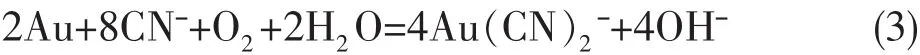
在单个浸出槽发生反应的过程称之为单级浸出。本文的机理模型由研究矿石浸出的原理出发,逐步建立浸出过程物料平衡方程及能量守恒方程。

单级浸出过程的输入为氰化钠流量、溶解氧浓度、矿石流量、矿浆浓度、粒子粒径,输出分别为浸出率、浸出后的矿石中金的品位、浸出后氰化钠浓度,以下推导单级浸出机理模型。浸出机理模型变量符号见表1。

表1 浸出机理模型变量符号

根据物料平衡原理,可以分别得到矿石的流量平衡方程、液体流量平衡方程：

式中：Qs0、Qs分别为浸出前后矿石的流量；Ql0、Ql分别为浸出前后液体的流量。

由固相中金守恒可得：

式中：QsCs0为初始流入浸出槽的金；QsCs为反应结束后流出浸出槽的金；MsrAu为反应掉的金。其中Cs0、Cs分别为浸出前后金的品位,Ms表示矿石的质量,rAu表示金浸出时的反应速率。

由液相中氰根守恒可得：

式中：QlCCN0为初始料液中的氰；QCN为添加进入浸出槽的氰；QlCCN为反应结束后剩余的氰；MlrCN为反应掉的氰。其中CCN0、CCN分别为浸出前后氰根的浓度,Ml表示矿液的质量,rCN表示氰的反应速率。

假设物料最大程度上混合,可得：

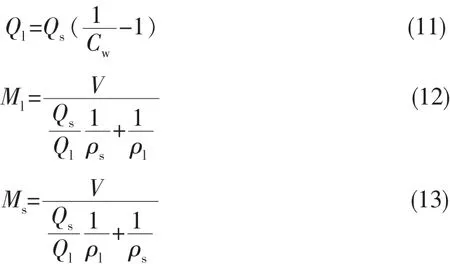
式中：Cw表示矿浆的浓度；Ml、Ms分别为液体的质量、矿石的质量；ρs、ρl分别表示矿石的密度、液体密度。

又因为物料充分混合,因此固体颗粒、液体和矿浆有相同的平均停留时间,可得：

式中：τ表示浸出过程反应时间。

浸出过程金粒的反应速率和氰化钠的消耗速率根据反应动力学可得到如下方程[6]：

上式表明，金的反应速率模型与矿石粒径、反应前后金品位、氰及氧的浓度相关；氰根反应的速率模型与矿石粒径、氰浓度相关。其中,d表示矿石的粒径；Cs、Cs∞分别表示当前时刻金的浓度、反应后金的理想最终浓度。a1～a6、b1～b4分别为反应动力学方程中的参数。查询相应文献可得到理想情况下矿石中金的最终浓度为：

综合上述各式，把式(11)、式(12)、式(16)代入式(10)便可求得氰根离子浓度。然后把式(11)、式(13)、式(15)、式(17)代入式(9)便可求得固相中金的浓度。由固相中金浓度的变化,便可求得金的浸出率X为式(18)：

机理模型中参数众多,确定准确的参数是模型成功的关键,本模型中的参数可分为3种：现场已知参数、查阅文献得到的参数、实验所得参数及辨识所得参数。其中,根据现场的实际情况有如下已知参数：V=68 m3；Qs=2 540 kg/h；Cw=0.33；CCN0=0；d=80 μm。而经笔者查阅相关的文献资料后,进而又确定了模型中的一部分参数[5]：rho_s=2.8 g/cm3；rho_l=1 g/cm3。实际生产过程中浸出槽中会安置溶氧仪,因此溶氧量CO可作为已知的参数作为模型的输入。机理模型中最主要的动力学参数：金和氰化钠的反应速率，是一个与粒径和初始金品位和浸出后金品位、氰化钠浓度和溶解氧浓度有关的可变参数,根据相关浸出过程建模文献[7]：

3 模型仿真分析

为了验证模型的可靠性,从现场采集最终浸出率样本20个,与机理模型预测值进行比较，结果如图2所示。

图2 浸出率预测结果

机理模型的性能采用最大误差(EMAX)、均方根误差(RMSE)、相对均方根误差(RRMSE)以及拟合度(RR)来验证,误差如表2所示。

表2 机理模型性能评价

图2和表2表明,所建浸出过程机理模型对浸出率的预测趋势与实际相符,但还存在较大的误差。故可以认为机理模型原理和结构正确,但模型内部参数与实际过程存在误差。

4 总结

本文建立了金的氰化浸出机理模型,考虑各种影响浸出率的因素,以金反应速率的动力学模型为基础,根据物料平衡和能量平衡关系,建立了浸出过程的机理模型,并通过实际数据验证了模型的可靠性。但浸出过程的影响因素很多,由于不同工业现场工艺流程复杂,设备类型多样,限制了这一模型的应用,需采用实际生产数据对模型中重要参数进行辨识,以提高模型准确性[8]。

[1] 简椿林.黄金冶炼技术综述[J].湿法冶金,2005,27(1):1-5.

[2] 陈家镛,杨守志,柯家骏,等.湿法冶金的研究与发展[M].北京:冶金工业出版社,1998：1-3.

[3] 胡广浩,毛志忠,周俊武,等.湿法冶金浸出过程建模与仿真研究[J].系统仿真学报,2011,23(6):1220-1224.

[4] 潘惊雷.湿法冶金浸出过程建模与优化[D].沈阳:东北大学,2012.

[5] L.R.P.de Andrade Lima,D.Hodouin.Optimization of reactor volumes for gold cyanidation[J].Minerals Engineering,2005,18(5): 671-679.

[6] Frank K Crundwell,Sven A Godorr.A mathematical model of the leaching of gold in cyanide solutions[J].Hydrometallurgy,1997,44 (1):147-162.

[7] Li Bao,Anh V Nguyen.Developing a physically consistent model for gibbsite leaching kinetics [J].Hydrometallurgy,2010,104(12): 86-98.

[8] 贾润达.湿法冶金萃取过程组分浓度软测量方法的研究与应用[D].沈阳:东北大学,2011.

Mechanism Model in Process of Hydrometallurgical Leaching

ZHOU Tianchi
(Jiangxi Nerin Electric Automation Co.,Ltd.,Nanchang,Jiangxi 330031,China)

For actual process of a certain Shandong gold refinery plant,taking gold leaching process (sodium cyanide is considered as leaching agent)as background,mechanism model of gold cyanide leaching is established based on relationship of materials and energy balance,model simulation is carried out through actual data to verify availability and generalization of model.

hydrometallurgy;gold;leaching process;mechanism model;leaching rate

TP15

A

1004-4345(2014)04-0040-03

2014-06-06

周天驰(1990—),男,主要从事有色冶金行业仪表自动化设计工作,研究方向为复杂工业过程建模及优化。